> 
> rm(list=ls())
> 
> rnorm2 <- function(n,mean,sd){ 
+   mean+sd*scale(rnorm(n)) 
+ }
> 
> n.p <- 100000
> m.p <- 100
> sd.p <- 10
> p1 <- rnorm2(n.p, m.p, sd.p)
> m.p1 <- mean(p1)
> sd.p1 <- sd(p1)
> 
> p2 <- rnorm2(n.p, m.p+4, sd.p)
> m.p2 <- mean(p2)
> sd.p2 <- sd(p2)
> 
> n.s <- 900
> se.z1 <- c(sqrt(var(p1)/n.s))
> se.z2 <- c(sqrt(var(p2)/n.s))
> se.z1
[1] 0.3333333
> se.z2
[1] 0.3333333
> 
> x.p1 <- seq(mean(p1)-5*se.z1, 
+             mean(p2)+5*se.z1, 
+             length.out = 500)
> x.p2 <- seq(mean(p2)-5*se.z1, 
+             mean(p2)+5*se.z1, 
+             length.out = 500)
> 
> # Calculate the probability 
> # density for a normal distribution
> y.p1 <- dnorm(x.p1, mean(p1), se.z1)
> y.p2 <- dnorm(x.p2, mean(p2), se.z2)
> 
> # Plot the theoretical PDF
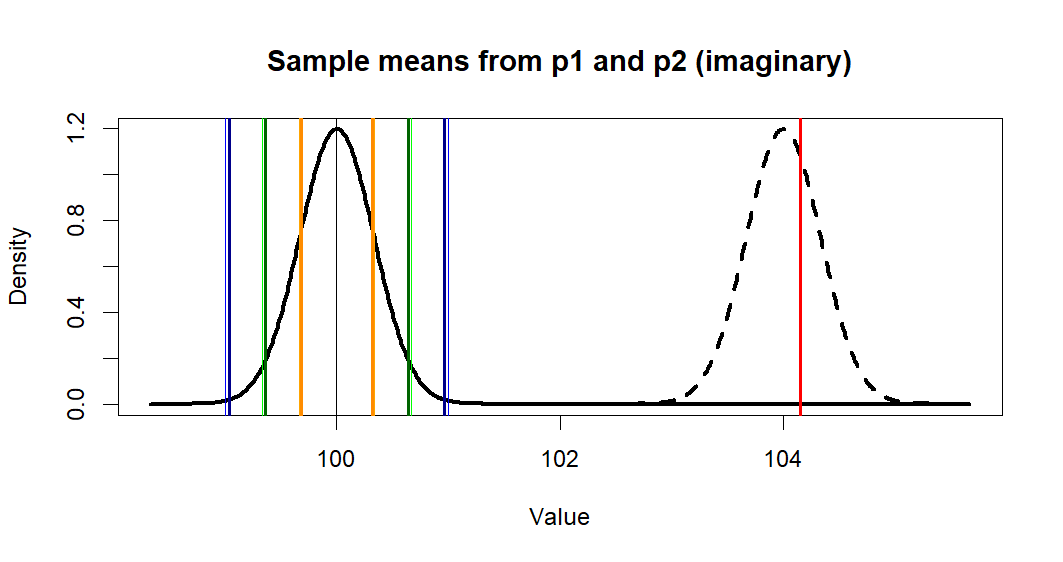
> plot(x.p1, y.p1, type = "l", 
+      lwd=3, 
+      main = "Sample means from p1 and p2 (imaginary)",
+      xlab = "Value", ylab = "Density")
> lines(x.p2, y.p2, lty=2, lwd=3)
> 
> 
> m.p1 <- mean(p1)
> se1 <- c(m.p1-se.z1, m.p1+se.z1)
> se2 <- c(m.p1-2*se.z1, m.p1+2*se.z1)
> se3 <- c(m.p1-3*se.z1, m.p1+3*se.z1)
> abline(v=c(m.p1,se1,se2,se3), 
+        col=c('black', 'orange', 'orange', 
+              'green', 'green', 
+              'blue', 'blue'), 
+        lwd=1)
> 
> treated.s <- sample(p2, n.s)
> m.treated.s <- mean(treated.s)
> abline(v=m.treated.s, col='red', lwd=2)
> 
> diff <- m.treated.s-mean(p1)
> diff/se.z1
[1] 12.46458
> zscore <- diff/se.z1
> pnorm(zscore, lower.tail = F)*2
[1] 1.164855e-35
> tscore <- zscore
> pt(tscore, df=length(treated.s)-1, lower.tail = F)*2
[1] 5.228928e-33
> 
> # usual way - using sample's variance 
> # instead of p1's variance to get
> # standard error value
> se.s <- sqrt(var(treated.s)/n.s)
> se.s
[1] 0.321227
> tscore <- diff/se.s
> tscore
[1] 12.93434
> 
> 
> se1 <- c(m.p1-se.s, m.p1+se.s)
> se2 <- c(m.p1-2*se.s, m.p1+2*se.s)
> se3 <- c(m.p1-3*se.s, m.p1+3*se.s)
> abline(v=c(se1,se2,se3), 
+        col=c('darkorange', 'darkorange',
+              'darkgreen', 'darkgreen', 
+              'darkblue', 'darkblue'), 
+        lwd=2)
> 
> 
> 
> 
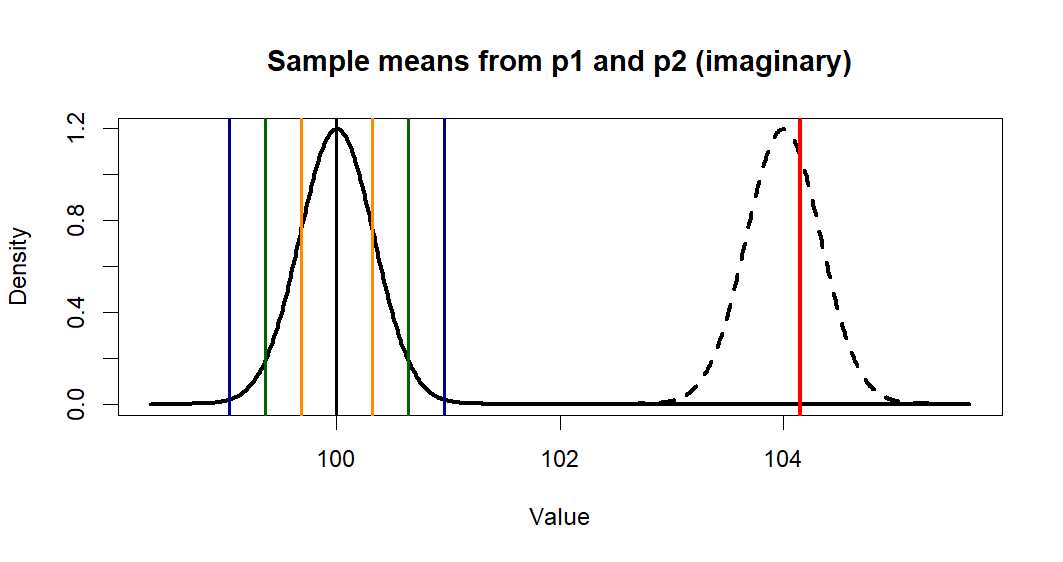
> plot(x.p1, y.p1, type = "l", 
+      lwd=3, 
+      main = "Sample means from p1 and p2 (imaginary)",
+      xlab = "Value", ylab = "Density")
> lines(x.p2, y.p2, lty=2, lwd=3)
> 
> 
> m.p1 <- mean(p1)
> se1 <- c(m.p1-se.s, m.p1+se.s)
> se2 <- c(m.p1-2*se.s, m.p1+2*se.s)
> se3 <- c(m.p1-3*se.s, m.p1+3*se.s)
> abline(v=c(m.p1,se1,se2,se3), 
+        col=c('black', 'darkorange', 'darkorange',
+              'darkgreen', 'darkgreen', 
+              'darkblue', 'darkblue'), 
+        lwd=2)
> abline(v=m.treated.s, col='red', lwd=3)
> se.s
[1] 0.321227
> se.z1
[1] 0.3333333
> 
> c(m.treated.s-2*se.s, m.treated.s+2*se.s)
[1] 103.5124 104.7973
> c <- qt(0.975, n.s-1)
> c
[1] 1.962606
> c(m.treated.s-c*se.s, m.treated.s+c*se.s)
[1] 103.5244 104.7853
> m.p2
[1] 104
> 
> x.p.est <- seq(m.treated.s-5*se.s, 
+                m.treated.s+5*se.z1, 
+                length.out = 500)
> y.p.est <- dnorm(x.p.est, m.treated.s, se.s)
> 
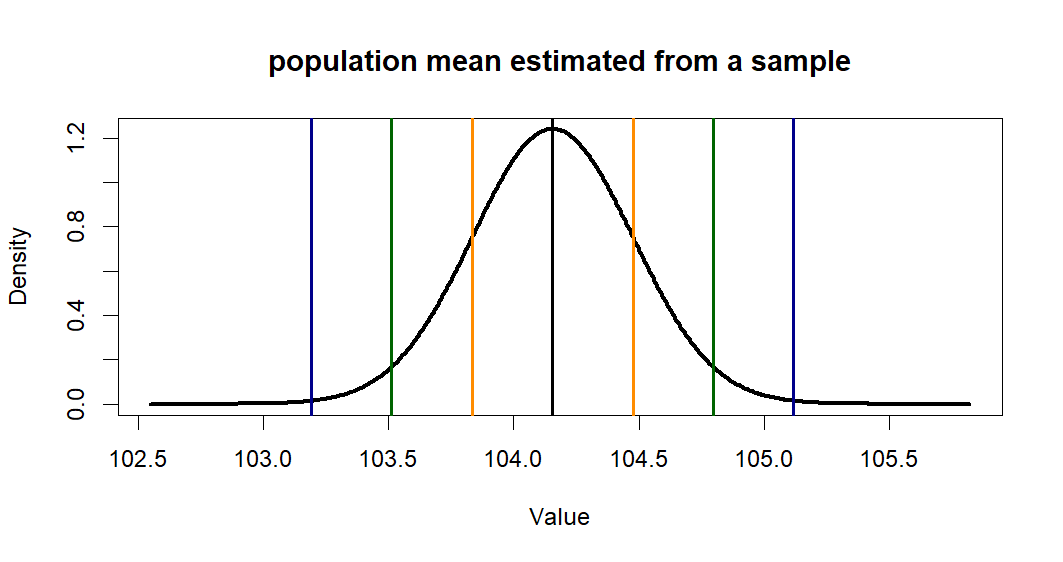
> plot(x.p.est, y.p.est, type = "l", 
+      lwd=3, 
+      main = "population mean estimated from a sample",
+      xlab = "Value", ylab = "Density")
> se1 <- c(m.treated.s-se.s, m.treated.s+se.s)
> se2 <- c(m.treated.s-2*se.s, m.treated.s+2*se.s)
> se3 <- c(m.treated.s-3*se.s, m.treated.s+3*se.s)
> abline(v=c(m.treated.s,se1,se2,se3), 
+        col=c('black', 'darkorange', 'darkorange',
+              'darkgreen', 'darkgreen', 
+              'darkblue', 'darkblue'), 
+        lwd=2)
> 
> 
> 
> 
> pt(diff/se.s, df=n.s-1, lower.tail = F) * 2
[1] 3.223219e-35
> t.test(treated.s, mu=m.p1, var.equal = T)

	One Sample t-test

data:  treated.s
t = 12.934, df = 899, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
 103.5244 104.7853
sample estimates:
mean of x 
 104.1549 

>