anova_note:output01
This is an old revision of the document!
>
> rm(list=ls())
> rnorm2 <- function(n,mean,sd) {
+ mean+sd*scale(rnorm(n))
+ }
> ss <- function(x) {
+ sum((x-mean(x))^2)
+ }
> set.seed(10)
> n <- 30
> n.o <- n.p <- n
> o <- rnorm(n.o, 100, 10)
> p <- rnorm(n.p, 104, 10)
>
> t.out <- t.test(o,p, var.equal=T)
> t.out
Two Sample t-test
data: o and p
t = -2.6941, df = 58, p-value = 0.009216
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-11.012446 -1.623742
sample estimates:
mean of x mean of y
96.55324 102.87133
>
> # old way
> m.o <- mean(o)
> m.p <- mean(p)
> df.o <- n.o - 1
> df.p <- n.p - 1
> diff <- m.o - m.p
> pv <- (ss(o)+ss(p))/(df.o+df.p)
> se <- sqrt((pv/n.o) + (pv/n.p))
> t.cal <- diff/se
> t.cal
[1] -2.694097
> pt(t.cal, df.o+df.p) * 2
[1] 0.009215657
> t.out$statistic
t
-2.694097
> t.out$p.value
[1] 0.009215657
>
> #
> comb <- list(o = o, p = p)
> op <- stack(comb)
> head(op)
values ind
1 100.18746 o
2 98.15747 o
3 86.28669 o
4 94.00832 o
5 102.94545 o
6 103.89794 o
> colnames(op)[1] <- "values"
> colnames(op)[2] <- "group"
> op$group <- factor(op$group)
> head(op)
values group
1 100.18746 o
2 98.15747 o
3 86.28669 o
4 94.00832 o
5 102.94545 o
6 103.89794 o
> boxplot(op$values~ss.o <- ss(o)
ss.p <- ss(p)
df.o <- length(o)-1
df.p <- length(p)-1
op$group)
>
>
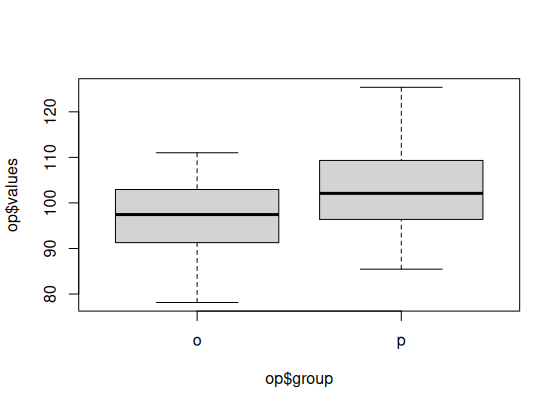
> plot(op$values~op$group)
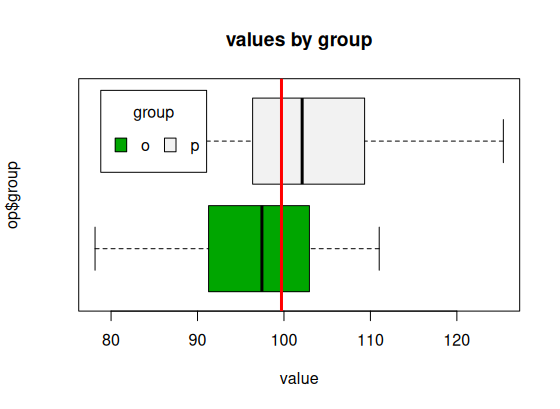
> boxplot(op$values~op$group, main="values by group",
+ yaxt="n", xlab="value", horizontal=TRUE,
+ col=terrain.colors(2))
> abline(v=mean(op$values), col="red", lwd=3)
> legend("topleft", inset=.05, title="group",
+ c("o","p"), fill=terrain.colors(2), horiz=TRUE)
>
>
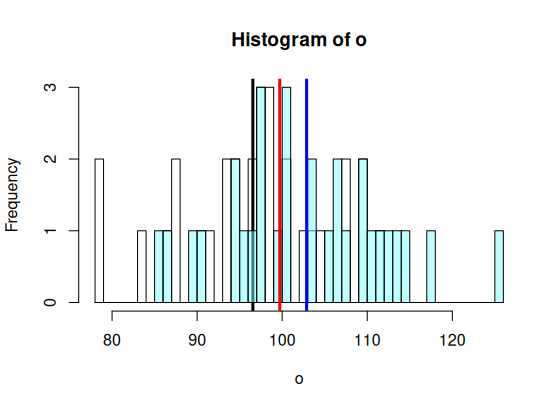
> m.tot <- mean(op$values) > m.o <- mean(o) > m.p <- mean(p) > > min.x <- min(op$values) > max.x <- max(op$values) > br <- seq(floor(min.x), ceiling(max.x), by = 1) > > hist(o, breaks=br, + col=rgb(1,1,1,.5)) > abline(v=m.o, col="black", lwd=3) > hist(p, add=T, breaks=br, + col=rgb(.5,1,1,.5)) > abline(v=m.p, col="blue", lwd=3) > abline(v=m.tot, col='red', lwd=3) >
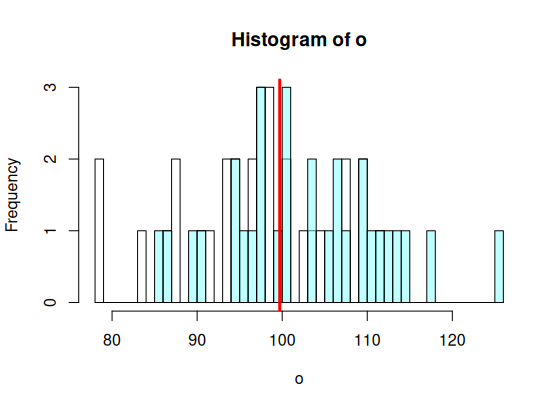
> hist(o, breaks=br, + col=rgb(1,1,1,.5)) > hist(p, add=T, breaks=br, + col=rgb(.5,1,1,.5)) > abline(v=m.tot, col='red', lwd=3) > > ss.tot <- ss(op$values) > df.tot <- length(op$values)-1 > ss.tot/df.tot [1] 91.24725 > var(op$values) [1] 91.24725 > ss.tot [1] 5383.588 >
> m.tot
[1] 99.71228
> m.o
[1] 96.55324
> m.p
[1] 102.8713
> ss.o
[1] 2179.19
> ss.p
[1] 2605.623
>
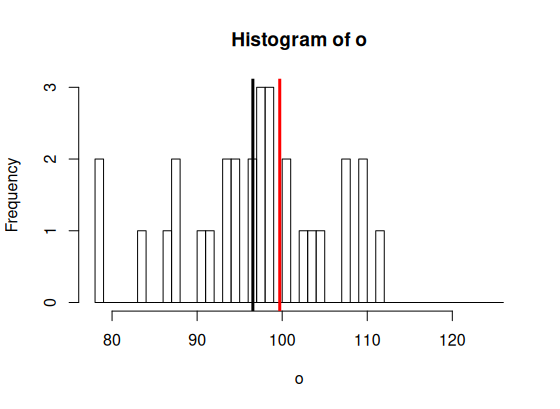
> hist(o, breaks=br,
+ col=rgb(1,1,1,.5))
> abline(v=m.o, col="black", lwd=3)
> abline(v=m.tot, col='red', lwd=3)
>
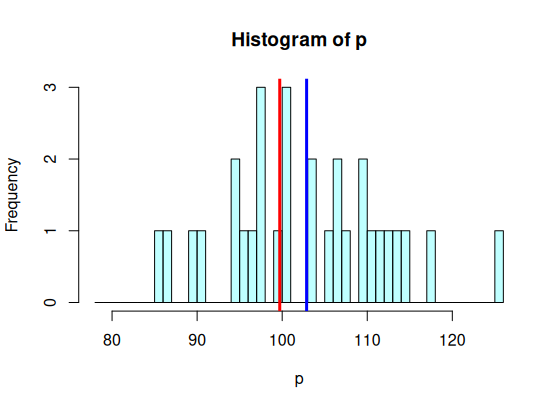
> hist(p, breaks=br,
+ col=rgb(.5,1,1,.5))
> abline(v=m.p, col="blue", lwd=3)
> abline(v=m.tot, col='red', lwd=3)
>
> ss.bet <- n.o*(m.tot-m.o)^2 + # m.tot 에서 o그룹공통 까지의 거리를 제곱해서 모두 더한 값
# 아래 그림에서 빨간색 선에서 검은색 선까지의 거리를 제곱해서 모두 더한 값
+ n.p*(m.tot-m.p)^2 # m.tot 에서 p그룹공통 까지의 거리를 제곱해서 모두 더한 값
# 아래 그림에서 빨간색 선에서 파란색 선까지의 거리를 제곱해서 모두 더한 값
# 이것은 그룹 (IV, 독립변인) 때문에 생긴 그룹 간 차이이다
> ss.bet # 따라서 이것을 SS between group이라고 부른다
[1] 598.7747
>
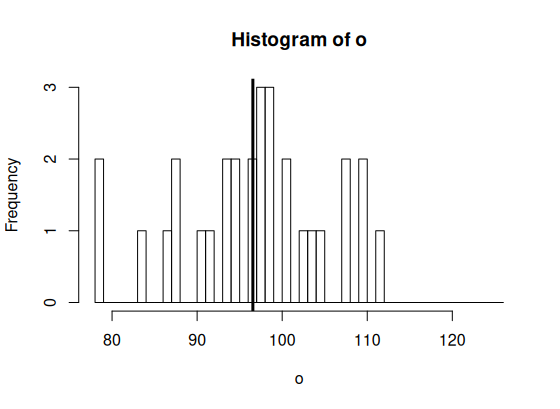
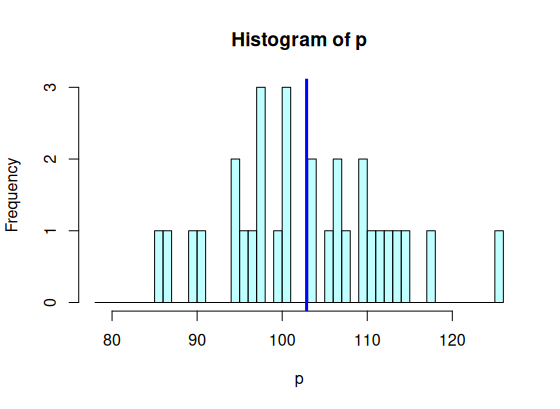
> hist(o, breaks=br, + col=rgb(1,1,1,.5)) > abline(v=m.o, col="black", lwd=3) > ss.o <- ss(o) # o집단의 평균인 검은색 선에서 개인 점수까지의 거리는 (오차는) 독립변인과 상관없이 랜덤하게 나타나는 것 > ss.o # o집단의 것을 ss.o라고 부른다 [1] 2179.19 > > hist(p, breaks=br, + col=rgb(.5,1,1,.5)) > abline(v=m.p, col="blue", lwd=3) > ss.p <- ss(p) # p집단도 마찬가지이다. 이 집단 내의 sum of square값은 p 집단의 공통특징인 평균에서 개인점수가 랜덤하게 > ss.p # 나타나는 것이고, 이것을 sum of square p라고 부른다 [1] 2605.623 > > # 이 둘은 random 한 차이이다 > ss.wit <- ss.o+ss.p > ss.wit [1] 4784.813 >
> ss.bet [1] 598.7747 > ss.wit [1] 4784.813 > ss.bet+ss.wit [1] 5383.588 > > ss.tot [1] 5383.588 >
> df.tot <- length(op$values)-1 > df.bet <- nlevels(op$group) - 1 > df.wit <- (n.o-1)+(n.p-1) > df.tot [1] 59 > df.bet [1] 1 > df.wit [1] 58 >
> ms.tot <- ss.tot / df.tot
> ms.bet <- ss.bet / df.bet
> ms.wit <- ss.wit / df.wit
>
> f.cal <- ms.bet / ms.wit
> f.cal
[1] 7.258158
> p.val <- pf(f.cal, df1=df.bet, df2=df.wit, lower.tail = F)
> p.val
[1] 0.009215657
> summary(aov(op$values~op$group))
Df Sum Sq Mean Sq F value Pr(>F)
op$group 1 599 598.8 7.258 0.00922 **
Residuals 58 4785 82.5
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> t.test(o,p, var.equal = T)
Two Sample t-test
data: o and p
t = -2.6941, df = 58, p-value = 0.009216
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-11.012446 -1.623742
sample estimates:
mean of x mean of y
96.55324 102.87133
>
> diff <- m.o - m.p
> ssp <- (ss.o + ss.p) / (df.o + df.p)
> se <- sqrt(ssp/n.o+ssp/n.p)
> t.cal <- diff/se
> t.cal
[1] -2.694097
> p.t.cal <- pt(abs(t.cal), df=df.o+df.p, lower.tail = F)*2
> p.t.cal
[1] 0.009215657
> t.cal^2
[1] 7.258158
> f.cal
[1] 7.258158
>
> df.bet
[1] 1
> df.wit
[1] 58
> f.cal
[1] 7.258158
>
anova_note/output01.1765320761.txt.gz · Last modified: by hkimscil