Table of Contents
data sample: diet.csv
Twoway ANOVA
recap of oneway ANOVA
# One Way Anova (Completely Randomized Design) fit <- aov(y ~ A, data=mydataframe)
Twoway ANOVA without interaction
# Randomized Block Design (B is the blocking factor) fit <- aov(y ~ A + B, data=mydataframe)
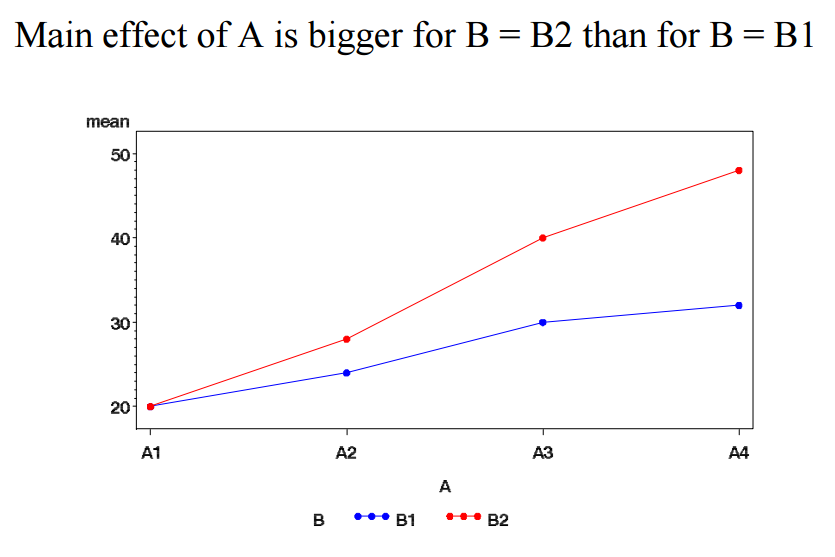
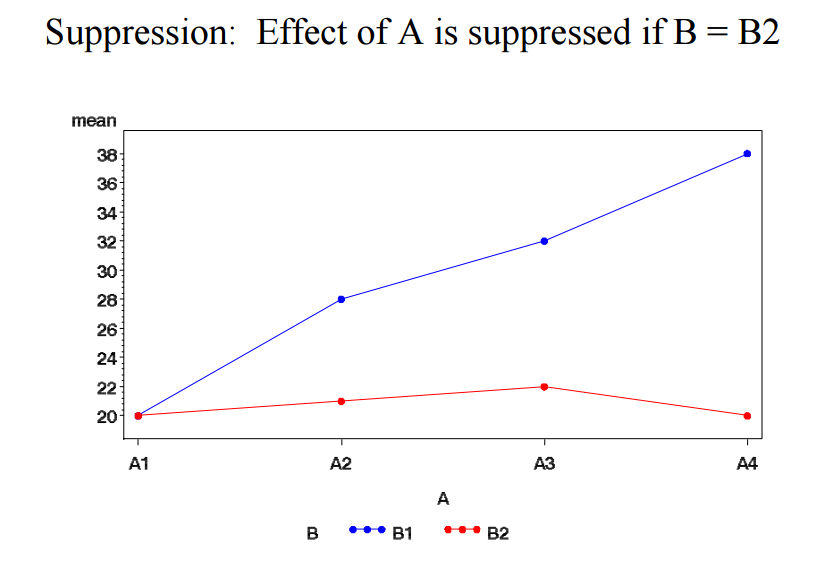
Twoway ANOVA with interaction
# Two Way Factorial Design fit <- aov(y ~ A + B + A:B, data=mydataframe) fit <- aov(y ~ A*B, data=mydataframe) # same thing
E.g. 1
> delivery.df = data.frame(
Service = c(rep("Carrier 1", 15), rep("Carrier 2", 15),
rep("Carrier 3", 15)),
Destination = c(rep(c("Office 1", "Office 2", "Office 3",
"Office 4", "Office 5"), 9)),
Time = c(15.23, 14.32, 14.77, 15.12, 14.05,
15.48, 14.13, 14.46, 15.62, 14.23, 15.19, 14.67, 14.48, 15.34, 14.22,
16.66, 16.27, 16.35, 16.93, 15.05, 16.98, 16.43, 15.95, 16.73, 15.62,
16.53, 16.26, 15.69, 16.97, 15.37, 17.12, 16.65, 15.73, 17.77, 15.52,
16.15, 16.86, 15.18, 17.96, 15.26, 16.36, 16.44, 14.82, 17.62, 15.04)
)
> delivery.df
Service Destination Time
1 Carrier 1 Office 1 15.23
2 Carrier 1 Office 2 14.32
3 Carrier 1 Office 3 14.77
4 Carrier 1 Office 4 15.12
5 Carrier 1 Office 5 14.05
6 Carrier 1 Office 1 15.48
7 Carrier 1 Office 2 14.13
8 Carrier 1 Office 3 14.46
9 Carrier 1 Office 4 15.62
10 Carrier 1 Office 5 14.23
11 Carrier 1 Office 1 15.19
12 Carrier 1 Office 2 14.67
13 Carrier 1 Office 3 14.48
14 Carrier 1 Office 4 15.34
15 Carrier 1 Office 5 14.22
16 Carrier 2 Office 1 16.66
17 Carrier 2 Office 2 16.27
18 Carrier 2 Office 3 16.35
19 Carrier 2 Office 4 16.93
20 Carrier 2 Office 5 15.05
21 Carrier 2 Office 1 16.98
22 Carrier 2 Office 2 16.43
23 Carrier 2 Office 3 15.95
24 Carrier 2 Office 4 16.73
25 Carrier 2 Office 5 15.62
26 Carrier 2 Office 1 16.53
27 Carrier 2 Office 2 16.26
28 Carrier 2 Office 3 15.69
29 Carrier 2 Office 4 16.97
30 Carrier 2 Office 5 15.37
31 Carrier 3 Office 1 17.12
32 Carrier 3 Office 2 16.65
33 Carrier 3 Office 3 15.73
34 Carrier 3 Office 4 17.77
35 Carrier 3 Office 5 15.52
36 Carrier 3 Office 1 16.15
37 Carrier 3 Office 2 16.86
38 Carrier 3 Office 3 15.18
39 Carrier 3 Office 4 17.96
40 Carrier 3 Office 5 15.26
41 Carrier 3 Office 1 16.36
42 Carrier 3 Office 2 16.44
43 Carrier 3 Office 3 14.82
44 Carrier 3 Office 4 17.62
45 Carrier 3 Office 5 15.04
> library("ggpubr")
> ggline(delivery.df, x = "Destination", y = "Time", color = "Service", add = c("mean_se", "dotplot"))
> delivery.mod1 = aov(Time ~ Destination*Service, data = delivery.df)
> summary(delivery.mod1)
Df Sum Sq Mean Sq F value Pr(>F)
Destination 4 17.5415 4.3854 61.1553 5.408e-14 ***
Service 2 23.1706 11.5853 161.5599 < 2.2e-16 ***
Destination:Service 8 4.1888 0.5236 7.3018 2.360e-05 ***
Residuals 30 2.1513 0.0717
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> TukeyHSD(delivery.mod1, which = "Service")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = Time ~ Destination * Service, data = delivery.df)
$Service
diff lwr upr p adj
Carrier 2-Carrier 1 1.498667 1.2576092 1.7397241 0.0000000
Carrier 3-Carrier 1 1.544667 1.3036092 1.7857241 0.0000000
Carrier 3-Carrier 2 0.046000 -0.1950575 0.2870575 0.8856246
E.g. 2
plant.df = PlantGrowth
plant.df$group = factor(plant.df$group,
labels = c("Control", "Treatment 1", "Treatment 2"))
require(ggplot2)
ggplot(plant.df, aes(x = group, y = weight)) +
geom_boxplot(fill = "grey80", colour = "blue") +
scale_x_discrete() + xlab("Treatment Group") +
ylab("Dried weight of plants")
> plant.mod2 = aov(weight ~ group, data = plant.df)
> summary(plant.mod2)
Df Sum Sq Mean Sq F value Pr(>F)
group 2 3.7663 1.8832 4.8461 0.01591 *
Residuals 27 10.4921 0.3886
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> TukeyHSD(plant.mod2)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = weight ~ group, data = plant.df)
$group
diff lwr upr p adj
Treatment 1-Control -0.371 -1.0622161 0.3202161 0.3908711
Treatment 2-Control 0.494 -0.1972161 1.1852161 0.1979960
Treatment 2-Treatment 1 0.865 0.1737839 1.5562161 0.0120064
plot(TukeyHSD(plant.mod2))
3
- basketball.txt
Time Shoes Made Morning Others 25 Morning Others 26 Night Others 27 Night Others 27 Morning Favorite 32 Morning Favorite 22 Night Favorite 30 Night Favorite 34 Morning Others 35 Morning Others 34 Night Others 33 Night Others 30 Morning Favorite 33 Morning Favorite 37 Night Favorite 36 Night Favorite 38
> basketball <- read.table("http://commres.net/wiki/_export/code/r/twoway_anova?codeblock=11",header=TRUE)
> basketball
Time Shoes Made
1 Morning Others 25
2 Morning Others 26
3 Night Others 27
4 Night Others 27
5 Morning Favorite 32
6 Morning Favorite 22
7 Night Favorite 30
8 Night Favorite 34
9 Morning Others 35
10 Morning Others 34
11 Night Others 33
12 Night Others 30
13 Morning Favorite 33
14 Morning Favorite 37
15 Night Favorite 36
16 Night Favorite 38
> attach(basketball)
>
> b.model <- aov(Made~Time+Shoes)
> summary(b.model)
Df Sum Sq Mean Sq F value Pr(>F)
Time 1 7.56 7.56 0.349 0.565
Shoes 1 39.06 39.06 1.802 0.202
Residuals 13 281.81 21.68
> b.model2 <- aov(Made~Time*Shoes)
> summary(b.model2)
Df Sum Sq Mean Sq F value Pr(>F)
Time 1 7.56 7.56 0.344 0.568
Shoes 1 39.06 39.06 1.777 0.207
Time:Shoes 1 18.06 18.06 0.822 0.382
Residuals 12 263.75 21.98
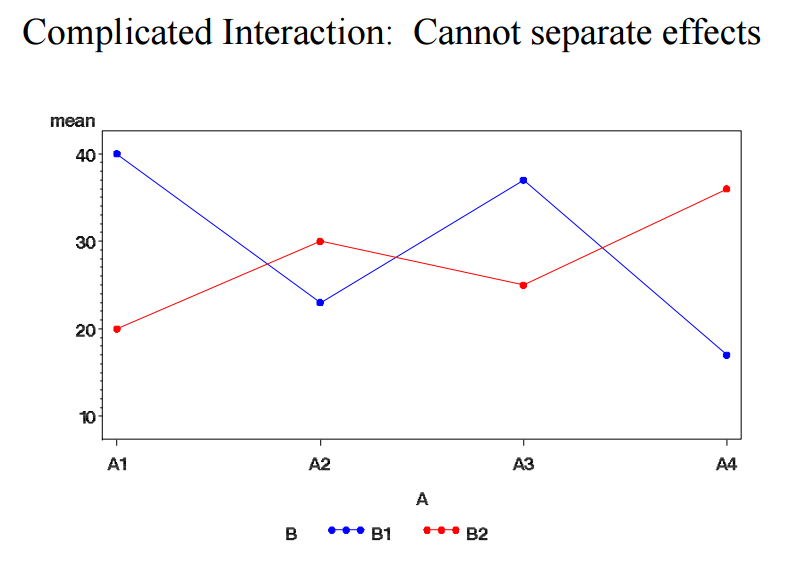
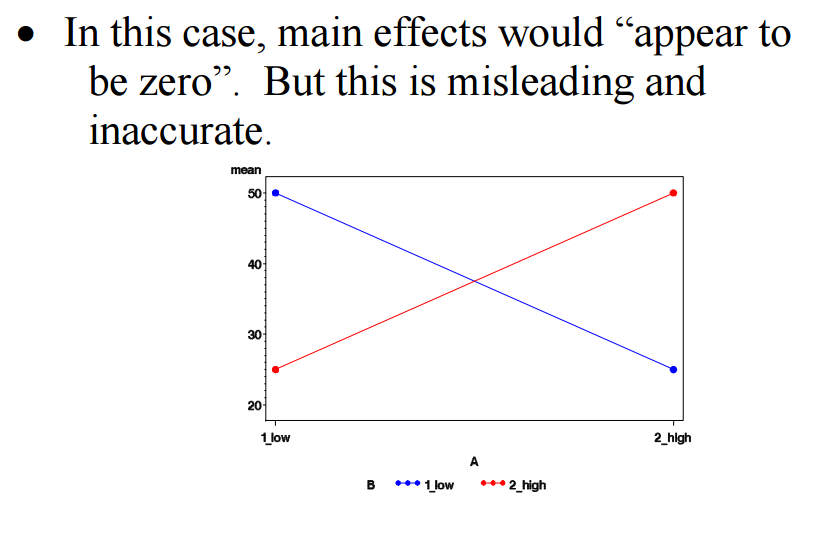
4 Interaction effects
e.g., 5
download dataset_anova_twoWay_interactions.csv
stressdata <- read.csv("http://commres.net/wiki/_media/r/dataset_anova_twoway_comparisons.csv")
> #display the data
> stressdata
Treatment Age StressReduction
1 mental young 10
2 mental young 9
3 mental young 8
4 mental mid 7
5 mental mid 6
6 mental mid 5
7 mental old 4
8 mental old 3
9 mental old 2
10 physical young 9
11 physical young 8
12 physical young 7
13 physical mid 6
14 physical mid 5
15 physical mid 4
16 physical old 3
17 physical old 2
18 physical old 1
19 medical young 8
20 medical young 7
21 medical young 6
22 medical mid 5
23 medical mid 4
24 medical mid 3
25 medical old 2
26 medical old 1
27 medical old 0
> stressdata <- read.csv("http://commres.net/wiki/_media/r/dataset_anova_twoway_comparisons.csv")
>
> a.mod <- aov(StressReduction~Treatment*Age, data=stressdata)
> summary(a.mod)
Df Sum Sq Mean Sq F value Pr(>F)
Treatment 2 18 9 9 0.00195 **
Age 2 162 81 81 1e-09 ***
Treatment:Age 4 0 0 0 1.00000
Residuals 18 18 1
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> TukeyHSD(a.mod, which="Treatment")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = StressReduction ~ Treatment * Age, data = stressdata)
$Treatment
diff lwr upr p adj
mental-medical 2 0.7968988 3.2031012 0.0013531
physical-medical 1 -0.2031012 2.2031012 0.1135025
physical-mental -1 -2.2031012 0.2031012 0.1135025
>
> TukeyHSD(a.mod, which="Age")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = StressReduction ~ Treatment * Age, data = stressdata)
$Age
diff lwr upr p adj
old-mid -3 -4.203101 -1.796899 1.54e-05
young-mid 3 1.796899 4.203101 1.54e-05
young-old 6 4.796899 7.203101 0.00e+00
>
위는 아래의 linear model 을 이용하여도 가능. 사실 모든 ANOVA 테스트는 linear model이기도 함(lm)
anova(lm(d$StressReduction ~ d$Treatment * d$Age, d))
Analysis of Variance Table
Response: d$StressReduction
Df Sum Sq Mean Sq F value Pr(>F)
d$Treatment 2 18 9 9 0.001953 **
d$Age 2 162 81 81 1e-09 ***
d$Treatment:d$Age 4 0 0 0 1.000000
Residuals 18 18 1
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
e.g., 6
tdata <- ToothGrowth
tdata
str(tdata)
tdata$dose <- factor(tdata$dose)
# or a nicer way
tdata$dose <- factor(tdata$dose, levels=c(0.5, 1, 2), labels=c("dhalf", "d1", "d2"))
tdata
table(tdata$supp, tdata$dose)
Visualize the data
install.packages("ggpubr")
library("ggpubr")
ggboxplot(tdata, x = "dose", y = "len", color = "supp",
palette = c("red", "blue"))
ggline(tdata, x = "dose", y = "len", color = "supp",
add = c("mean_se", "dotplot"),
palette = c("red", "blue"))
# prettier
boxplot(len ~ supp * dose, data=tdata, frame = FALSE,
col = c("#00AFBB", "#E7B800"), ylab="Tooth Length")
# or
interaction.plot(x.factor = tdata$dose, trace.factor =
tdata$supp, response = tdata$len, fun = mean,
type = "b", legend = TRUE,
xlab = "Dose", ylab="Tooth Length",
pch=c(1,19), col = c("#00AFBB", "#E7B800"))
Compute ANOVA test
res.aov2 <- aov(len ~ supp + dose, data = tdata)
summary(res.aov2)
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 14.02 0.000429 ***
dose 2 2426.4 1213.2 82.81 < 2e-16 ***
Residuals 56 820.4 14.7
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
res.aov3 <- aov(len ~ supp * dose, data = tdata)
res.aov3 <- aov(len ~ supp + dose + supp:dose, data = tdata)
summary(res.aov3)
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 15.572 0.000231 ***
dose 2 2426.4 1213.2 92.000 < 2e-16 ***
supp:dose 2 108.3 54.2 4.107 0.021860 *
Residuals 54 712.1 13.2
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
From the ANOVA results, you can conclude the following, based on the p-values and a significance level of 0.05:
- the p-value of supp is 0.000429 (significant), which indicates that the levels of supp are associated with significant different tooth length.
- the p-value of dose is < 2e-16 (significant), which indicates that the levels of dose are associated with significant different tooth length.
- the p-value for the interaction between supp*dose is 0.02 (significant), which indicates that the relationships between dose and tooth length depends on the supp method.
pair-wise test
> TukeyHSD(res.aov3, which = "dose")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = len ~ supp * dose, data = tdata)
$dose
diff lwr upr p adj
d1-dh 9.130 6.362488 11.897512 0.0e+00
d2-dh 15.495 12.727488 18.262512 0.0e+00
d2-d1 6.365 3.597488 9.132512 2.7e-06
pairwise.t.test(tdata$len, tdata$dose, p.adjust.method = "BH")
Homogeneity
plot(res.aov3, 1)
install.packages("car")
library(car)
leveneTest(len ~ supp*dose, data = tdata)
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 5 1.7086 0.1484
54
p value is greater than .05, which indicates that there is no evidence of significant difference between variances of groups.
check normality
plot(res.aov3, 2)
The residuals are plotted against the quantiles of normal distribution (the straight line).
unbalance design
> library(car)
> my_anova <- aov(len ~ supp * dose, data = tdata)
>
> Anova(my_anova, type="III"
+ )
Anova Table (Type III tests)
Response: len
Sum Sq Df F value Pr(>F)
(Intercept) 1750.33 1 132.730 3.603e-16 ***
supp 137.81 1 10.450 0.002092 **
dose 885.26 2 33.565 3.363e-10 ***
supp:dose 108.32 2 4.107 0.021860 *
Residuals 712.11 54
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1