100 문제가 있다. 문제 하나를 맞힐 확률은 1/4 이다. 어떤 사람이 30문제 보다 많이 맞힐 확률은 무엇인가?
30문제보다 많이 맞힐 = P(x > 30) 이라는 뜻
> dbinom(30, 100, 1/4) # 30문제 맞힐 확률을 말한다 [1] 0.04575381 > a <- pbinom(30, 100, 1/4) # 30문제까지 맞힐 확률을 말한다 > # 따라서 1 - a 는 31, 32, 33, 34, . . . . 100 문제 맞힐 확률을 말한다 > 1 - a [1] 0.1037872 > >
- code01
- output01
Loading...
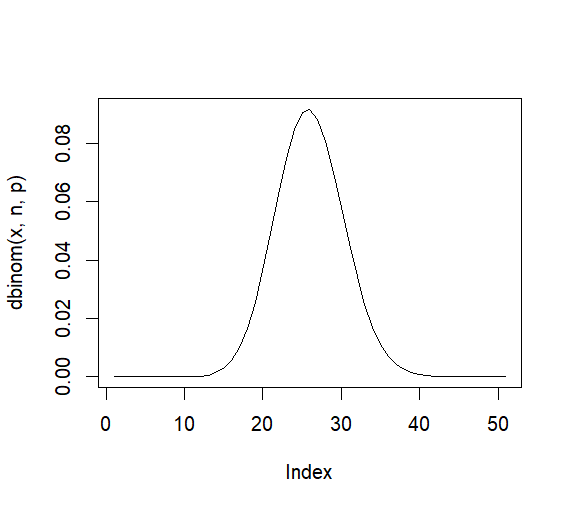
> 1 - pbinom(30, 100, 1/4) [1] 0.1037872 > pbinom(30, 100, 1/4, lower.tail = F) [1] 0.1037872 > > # 위의 문제를 normal distriubtion으로 계산한다면 > # exp(k) = np, var(k) = npq 이므로 > n <- 100 > p <- 1/4 > q <- 1-p > e.k <- n*p > v.k <- n*p*q > e.k [1] 25 > v.k [1] 18.75 > sd.k <- sqrt(v.k) > > x <- 0:50 > plot(dbinom(x, n, p), type="l") > # 위에서 P(x > 30) 을 묻는 문제 > pnorm(30, e.k, sd.k, lower.tail = F) [1] 0.1241065 > # cc를 적용하면 > pnorm(30.5, e.k, sd.k, lower.tail = F) [1] 0.1020119 > > # P(x<_25)? > pbinom(25, n, p) [1] 0.5534708 > pnorm(25, e.k, sd.k) [1] 0.5 > pnorm(25.5, e.k, sd.k) [1] 0.5459637 >
그러나, sample proportion을 기록하는 데이터는 binomial distribution이 아닌 normal distribution을 따름
- code02
- output02
Loading...
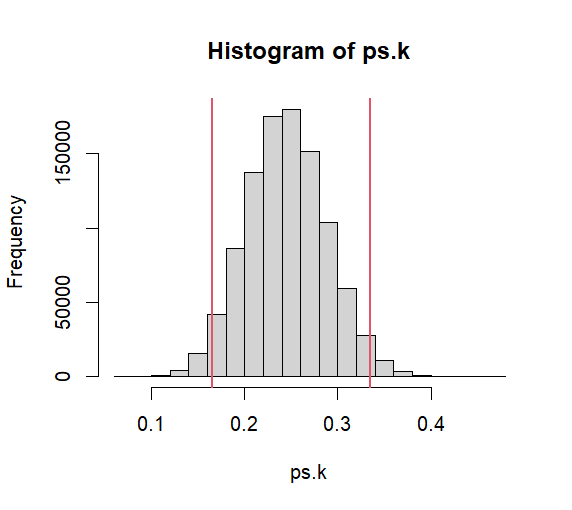
> set.seed(101) > k <- 1000 > n <- 100 > p <- 1/4 > q <- 1-p > # in order to clarify what we are doing > # X~B(n,p) 일 때, 100개의 검볼을 샘플링해서 > # red gumball을 세봤더니 > rbinom(1,n,p) # 24개 였다라는 뜻 [1] 24 > > # 아래는 이것을 1000번 (k번) 한 것 > numbers.of.red.gumball <- rbinom(k, n, p) > head(numbers.of.red.gumball) [1] 18 27 27 22 23 26 > > # 아래처럼 n으로 (100개의 검볼이 총 숫자이므로) > # 나눠주면 비율을 구할 수 있다 > proportions.of.rg <- numbers.of.red.gumball/n > ps.k <- proportions.of.rg > head(ps.k) [1] 0.18 0.27 0.27 0.22 0.23 0.26 > > mean.ps.k <- mean(ps.k) > mean.ps.k [1] 0.24893 > hist(ps.k) > > > #### > set.seed(101) > k <- 1000000 > n <- 100 > p <- 1/4 > q <- 1-p > numbers.of.red.gumball <- rbinom(k, n, p) > > # 아래처럼 n으로 (100개의 검볼이 총 숫자이므로) > # 나눠주면 비율을 구할 수 있다 > proportions.of.rg <- numbers.of.red.gumball/n > ps.k <- proportions.of.rg > mean.ps.k <- mean(ps.k) > mean.ps.k # 위에서 구한 시뮬레이션 샘플들의 평균 [1] 0.2500216 > > mean.value <- n * p # 이론적인 샘플비율들의 평균 > mean.value [1] 25 > > # variance? > var.cal <- var(ps.k) # 위에서 구한 시뮬레이션 샘플들의 분산 > var.cal [1] 0.001869 > var.value <- (p*q)/n # 교재가 증명한 이론적인 샘플비율들의 분산값 > var.value [1] 0.001875 > > # standard deviation > sd.cal <- sqrt(var.cal) > sd.cal [1] 0.04323193 > sd.value <- sqrt(var.value) > sd.value [1] 0.04330127 > > se <- sd.value > # 우리는 standard deviation of sample > # proportions을 standard error라고 부른다 > > # 위의 histogram 에서 mean 값은 이론적으로 > p [1] 0.25 > # standard deviation값은 > se [1] 0.04330127 > > qnorm(.975) [1] 1.959964 > # 우리는 평균값에서 +- 2*sd.cal 구간이 95%인줄 안다. > se2 <- se * qnorm(.975) > # 즉, 아래 구간이 > lower <- p-se2 > upper <- p+se2 > lower [1] 0.1651311 > upper [1] 0.3348689 > > hist(ps.k) > abline(v=lower, col=2, lwd=2) > abline(v=upper, col=2, lwd=2) > > a <- pnorm(lower, mean=p, sd=se) > b <- pnorm(upper, p, se) > b-a [1] 0.95 > lower [1] 0.1651311 > upper [1] 0.3348689 > > # 위의 그래프가 의미하는 것은 rbinom(1, n, p) / n로 > # 얻은 하나의 샘플의 proportion의 (비율) 값은 > # 95/100 확률로 lower에서 upper사이에 있을 것이라는 > # 뜻 > rbinom(1, n, p)/n [1] 0.29 > rbinom(1, n, p)/n [1] 0.24 > > k <- 100 > sa1 <- rbinom(k, n, p) / n > head(sa1) [1] 0.29 0.29 0.23 0.23 0.27 0.29 > sa1 < lower [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE [12] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE [23] FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE [34] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [45] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [56] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [67] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [78] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [89] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [100] FALSE > sa1 > upper [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [12] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [23] TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [34] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [45] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [56] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [67] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [78] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [89] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE [100] FALSE > table(sa1 < lower) FALSE TRUE 96 4 > table(sa1 > upper) FALSE TRUE 99 1 > > table(sa1 < lower | sa1 > upper) FALSE TRUE 95 5 > table(sa1 < lower | sa1 > upper) / k FALSE TRUE 0.95 0.05