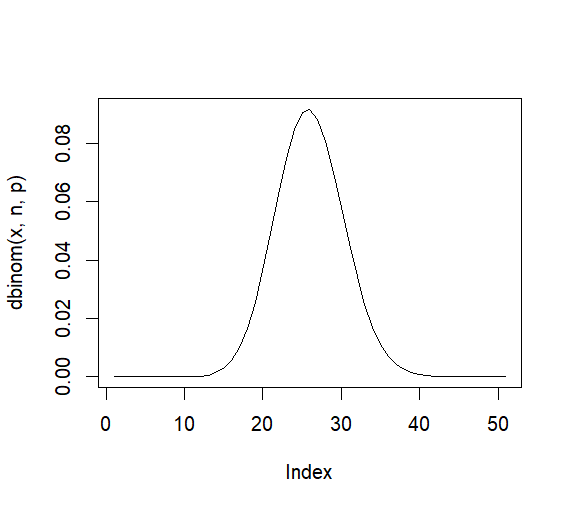
> 1 - pbinom(30, 100, 1/4) [1] 0.1037872 > pbinom(30, 100, 1/4, lower.tail = F) [1] 0.1037872 > > # 위의 문제를 normal distriubtion으로 계산한다면 > # exp(k) = np, var(k) = npq 이므로 > n <- 100 > p <- 1/4 > q <- 1-p > e.k <- n*p > v.k <- n*p*q > e.k [1] 25 > v.k [1] 18.75 > sd.k <- sqrt(v.k) > > x <- 0:50 > plot(dbinom(x, n, p), type="l") > # 위에서 P(x > 30) 을 묻는 문제 > pnorm(30, e.k, sd.k, lower.tail = F) [1] 0.1241065 > # cc를 적용하면 > pnorm(30.5, e.k, sd.k, lower.tail = F) [1] 0.1020119 > > # P(x<_25)? > pbinom(25, n, p) [1] 0.5534708 > pnorm(25, e.k, sd.k) [1] 0.5 > pnorm(25.5, e.k, sd.k) [1] 0.5459637 >