t-test summing up
t-test summing up output
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8 t-test and anova
- 9
- 10
- 11
- 12

t-test summing up

rm(list=ls())
rnorm2 <- function(n,mean,sd){ 
  mean+sd*scale(rnorm(n)) 
}
se <- function(sample) {
  sd(sample)/sqrt(length(sample))
}
ss <- function(x) {
  sum((x-mean(x))^2)
}

N.p <- 100000
m.p <- 100
sd.p <- 10


p1 <- rnorm2(N.p, m.p, sd.p)
mean(p1)
sd(p1)

p2 <- rnorm2(N.p, m.p+10, sd.p)
mean(p2)
sd(p2)

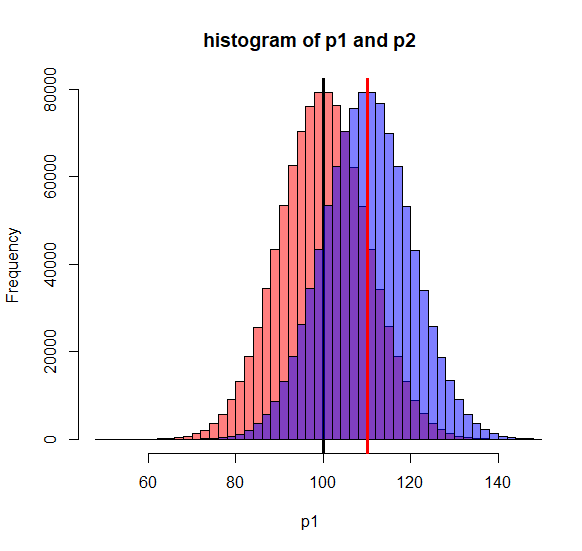
hist(p1, breaks=50, col = rgb(1, 0, 0, 0.5),
     main = "histogram of p1 and p2",)
abline(v=mean(p1), col="black", lwd=3)
hist(p2, breaks=50, add=TRUE, col = rgb(0, 0, 1, 0.5))
abline(v=mean(p2), col="red", lwd=3)

# but suppose that we do not
# know the parameter of p2.
# But, the real effect of the 
# drug is 10 point improvement
# (mean = 110). 

hist(p1, breaks=50, col = rgb(1, 0, 0, 0.5),
     main = "histogram of p1",)
abline(v=mean(p1), col="black", lwd=3)

# we take 100 random sample 
# (from p2)
s.size <- 100
s2 <- sample(p2, s.size)
mean(s2)
sd(s2)

# The sample statistics are
# our clue to prove the 
# effectiveness of the drug. 

# Let's assume that the drug is
# NOT effective. And we also assume
# the distribution of sample means
# whose sample size is 100 (in this
# case).

se.z <- sqrt(var(p1)/s.size)
se.z <- c(se.z)

z.cal <- (mean(s2) - mean(p1)) / se.z
z.cal
pnorm(z.cal, lower.tail = F) * 2

# So, 
iter <- 100000
means <- rep(NA, iter)
# means <- c()
for (i in 1:iter) {
  m.of.s <- mean(sample(p1, s.size))
  # means <- append(means, m.of.s)
  means[i] <- m.of.s
}

hist(means, 
     xlim = c(mean(means)-3*sd(means), 
              mean(means)+10*sd(means)), 
     col = rgb(0, 0, 0, 0))
abline(v=mean(p1), col="black", lwd=3)
abline(v=mean(s2), 
       col="blue", lwd=3)
lo1 <- mean(p1)-se.z
hi1 <- mean(p1)+se.z
lo2 <- mean(p1)-2*se.z
hi2 <- mean(p1)+2*se.z
abline(v=c(lo1, hi1, lo2, hi2), 
       col=c("green","green", "brown", "brown"), 
       lwd=2)
se.z
c(lo2, hi2)
pnorm(z.cal, lower.tail = F) * 2


# Note that we use sqrt(var(s2)/s.size)
# as our se value instread of 
# sqrt(var(p1)/s.size)
# This is a common practice for R
# In fact, some z.test (made by someone)
# function uses the former rather than
# latter.

sqrt(var(p1)/s.size)
se.z

sqrt(var(s2)/s.size)
se(s2)
se.s <- se(s2)


t.cal.os <- (mean(s2) - mean(p1))/ se.s 
z.cal <- (mean(s2) - mean(p1)) / se.z

t.cal.os
z.cal 

df.s2 <- length(s2) - 1
df.s2
p.t.os <- pt(abs(t.cal.os), 
             df.s2, 
             lower.tail = F) * 2

t.out <- t.test(s2, mu=mean(p1))
t.out
t.cal.os 
p.t.os

########################
# 2 sample t-test
########################
# 가정. 아래에서 추출하는 두 
# 샘플의 모집단의 파라미터를
# 모른다. 
s1 <- sample(p1, s.size)
s2 <- sample(p2, s.size)

mean(s1)
mean(s2)
ss(s1)
ss(s2)
df.s1 <- length(s1)-1
df.s2 <- length(s2)-1
df.s1
df.s2

pooled.variance <- (ss(s1)+ss(s2))/(df.s1+df.s2)
pooled.variance
se.ts <- sqrt((pooled.variance/length(s1))+(pooled.variance/length(s2)))
se.ts
t.cal.ts <- (mean(s1)-mean(s2))/se.ts
t.cal.ts
p.val.ts <- pt(abs(t.cal.ts), df=df.s1+df.s2, lower.tail = F) * 2
p.val.ts

t.out <- t.test(s1, s2, var.equal = T)
t.out

hist(s1, breaks=30,
     col = rgb(1, 0, 0, 0.5))
hist(s2, breaks=30, add=T, col=rgb(0,0,1,1))
abline(v=mean(s1), col="green", lwd=3)
# hist(s2, breaks=50, add=TRUE, col = rgb(0, 0, 1, 0.5))
abline(v=mean(s2), col="lightblue", lwd=3)

diff <- (mean(s1)-mean(s2))
diff
se.ts 
diff/se.ts
t.out$statistic

####
# repeated measure t-test
# we can use the above case 
# pop paramter unknown
# two consecutive measurement 
# for the same sample 

t1 <- s1
t2 <- s2
mean(t1)
mean(t2)
diff.s <- t1 - t2
head(diff.s)
t.cal.rm <- mean(diff.s)/se(diff.s)
t.cal.rm
p.val.rm <- pt(abs(t.cal.rm), 
               length(s1)-1, 
               lower.tail = F) * 2
p.val.rm
t.test(s1, s2, paired = T)

# 2 샘플 히스토그램을 이용해서
# anova 설명하기 
s.all <- c(s1,s2)
mean(s.all) # 두 집단을 합친 
# 종속변인의 평균 (아래 히스토
# 그램에서 검정색).
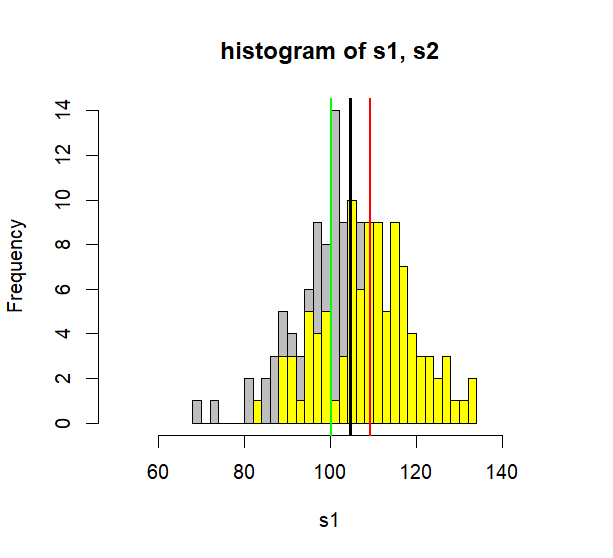
hist(s1, col='grey', breaks=30, xlim=c(50, 150),
     main = "histogram of s1, s2")
hist(s2, col='yellow', breaks=30, add=TRUE)
abline(v=c(mean(s.all)), 
       col=c("black"), lwd=3)
abline(v=c(mean(s1), mean(s2)), 
       col=c("green", "red"), lwd=2)

comb <- data.frame(s1,s2)
dat <- stack(comb)
head(dat)
tail(dat)

m.tot <- mean(s.all)
m.s1 <- mean(s1)
m.s2 <- mean(s2)

ss.tot <- ss(s.all)
bet.s1 <- (m.tot - m.s1)^2 * length(s1)
bet.s2 <- (m.tot - m.s2)^2 * length(s2)
ss.bet <- bet.s1 + bet.s2
ss.s1 <- ss(s1)
ss.s2 <- ss(s2)
ss.wit <- ss.s1+ss.s2

ss.tot
ss.bet
ss.wit
ss.bet+ss.wit

df.tot <- length(s.all) - 1
df.bet <- nlevels(dat$ind) - 1
df.s1 <- length(s1)-1
df.s2 <- length(s2)-1
df.wit <- df.s1 + df.s2

df.tot
df.bet
df.wit
df.bet+df.wit

ss.tot/df.tot
ms.tot <- ss.tot/df.tot

ms.bet <- ss.bet / df.bet
ms.wit <- ss.wit / df.wit

f.cal <- ms.bet / ms.wit
f.cal
pf(f.cal, df.bet, df.wit, lower.tail = F)

f.test <-  aov(dat$values~ dat$ind, data = dat)
sum.f.test <- summary(f.test)
sum.f.test


sum.f.test[[1]][1,4]
sum.f.test[[1]][1,5]
sqrt(f.cal)
t.cal.ts

# the above is anova after all. 

m1 <- lm(dat$values~dat$ind, data = dat)
sum.m1 <- summary(m1)
sum.m1

sum.m1$r.square
ss.bet # 독립변인인 s1, s2의 그룹
# 구분으로 설명된 ss.tot 중의 일부
ss.tot # y 전체의 uncertainty
ss.bet/ss.tot

sum.m1$fstatistic[1]
ms.bet/ms.wit

t-test summing up output

1

> rm(list=ls())
> rnorm2 <- function(n,mean,sd){ 
+   mean+sd*scale(rnorm(n)) 
+ }
> se <- function(sample) {
+   sd(sample)/sqrt(length(sample))
+ }
> ss <- function(x) {
+   sum((x-mean(x))^2)
+ }
>

EXP.

필요한 펑션들
se standard error 값을 구하는 펑션
ss sum of square 값을 구하는 펑션

2

> N.p <- 100000
> m.p <- 100
> sd.p <- 10
> 
> 
> p1 <- rnorm2(N.p, m.p, sd.p)
> mean(p1)
[1] 100
> sd(p1)
[1] 10
> 
> p2 <- rnorm2(N.p, m.p+10, sd.p)
> mean(p2)
[1] 110
> sd(p2)
[1] 10
> 
> hist(p1, breaks=50, col = rgb(1, 0, 0, 0.5),
+      main = "histogram of p1 and p2",)
> abline(v=mean(p1), col="black", lwd=3)
> hist(p2, breaks=50, add=TRUE, col = rgb(0, 0, 1, 0.5))
> abline(v=mean(p2), col="red", lwd=3)
> 
> # but suppose that we do not
> # know the parameter of p2.
> # But, the real effect of the 
> # drug is 10 point improvement
> # (mean = 110). 
>

3

> # we take 100 random sample 
> # (from p2)
> s.size <- 100
> s2 <- sample(p2, s.size)
> mean(s2)
[1] 109.5224
> sd(s2)
[1] 9.996692
> 
> # The sample statistics are
> # our clue to prove the 
> # effectiveness of the drug. 
> 
> # Let's assume that the drug is
> # NOT effective. And we also assume
> # the distribution of sample means
> # whose sample size is 100 (in this
> # case).
> 
> se.z <- sqrt(var(p1)/s.size)
> se.z <- c(se.z)
> 
> z.cal <- (mean(s2) - mean(p1)) / se.z
> z.cal
[1] 9.522449
> pnorm(z.cal, lower.tail = F) * 2
[1] 1.691454e-21
>

…………………………..

4

> # So, 
> iter <- 100000
> means <- rep(NA, iter)
> # means <- c()
> for (i in 1:iter) {
+   m.of.s <- mean(sample(p1, s.size))
+   # means <- append(means, m.of.s)
+   means[i] <- m.of.s
+ }
> 
> hist(means, 
+      xlim = c(mean(means)-3*sd(means), 
+               mean(means)+10*sd(means)), 
+      col = rgb(0, 0, 0, 0))
> abline(v=mean(p1), col="black", lwd=3)
> abline(v=mean(s2), 
+        col="blue", lwd=3)
> lo1 <- mean(p1)-se.z
> hi1 <- mean(p1)+se.z
> lo2 <- mean(p1)-2*se.z
> hi2 <- mean(p1)+2*se.z
> abline(v=c(lo1, hi1, lo2, hi2), 
+        col=c("green","green", "brown", "brown"), 
+        lwd=2)
> se.z
[1] 1
> c(lo2, hi2)
[1]  98 102
> pnorm(z.cal, lower.tail = F) * 2
[1] 1.691454e-21
> 
>

…………………………..

5

> # Note that we use sqrt(var(s2)/s.size)
> # as our se value instread of 
> # sqrt(var(p1)/s.size)
> # This is a common practice for R
> # In fact, some z.test (made by someone)
> # function uses the former rather than
> # latter.
> 
> sqrt(var(p1)/s.size)
     [,1]
[1,]    1
> se.z
[1] 1
> 
> sqrt(var(s2)/s.size)
[1] 0.9996692
> se(s2)
[1] 0.9996692
> se.s <- se(s2)
> 
> 
> t.cal.os <- (mean(s2) - mean(p1))/ se.s 
> z.cal <- (mean(s2) - mean(p1)) / se.z
> 
> t.cal.os
[1] 9.5256
> z.cal 
[1] 9.522449
> 
> df.s2 <- length(s2) - 1
> df.s2
[1] 99
> p.t.os <- pt(abs(t.cal.os), 
+              df.s2, 
+              lower.tail = F) * 2
> 
> t.out <- t.test(s2, mu=mean(p1))
> t.out

	One Sample t-test

data:  s2
t = 9.5256, df = 99, p-value = 1.186e-15
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
 107.5389 111.5060
sample estimates:
mean of x 
 109.5224 

> t.cal.os 
[1] 9.5256
> p.t.os
[1] 1.185895e-15
>

…………………………..

6

> ########################
> # 2 sample t-test
> ########################
> # 가정. 아래에서 추출하는 두 
> # 샘플의 모집단의 파라미터를
> # 모른다. 
> s1 <- sample(p1, s.size)
> s2 <- sample(p2, s.size)
> 
> mean(s1)
[1] 100.3577
> mean(s2)
[1] 110.1579
> ss(s1)
[1] 7831.618
> ss(s2)
[1] 7809.363
> df.s1 <- length(s1)-1
> df.s2 <- length(s2)-1
> df.s1
[1] 99
> df.s2
[1] 99
> 
> pooled.variance <- (ss(s1)+ss(s2))/(df.s1+df.s2)
> pooled.variance
[1] 78.99486
> se.ts <- sqrt((pooled.variance/length(s1))+(pooled.variance/length(s2)))
> se.ts
[1] 1.25694
> t.cal.ts <- (mean(s1)-mean(s2))/se.ts
> t.cal.ts
[1] -7.79685
> p.val.ts <- pt(abs(t.cal.ts), df=df.s1+df.s2, lower.tail = F) * 2
> p.val.ts
[1] 3.537633e-13
> 
> t.out <- t.test(s1, s2, var.equal = T)
> t.out

	Two Sample t-test

data:  s1 and s2
t = -7.7969, df = 198, p-value = 3.538e-13
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -12.278877  -7.321463
sample estimates:
mean of x mean of y 
 100.3577  110.1579 

> 
> hist(s1, breaks=30,
+      col = rgb(1, 0, 0, 0.5))
> hist(s2, breaks=30, add=T, col=rgb(0,0,1,1))
> abline(v=mean(s1), col="green", lwd=3)
> # hist(s2, breaks=50, add=TRUE, col = rgb(0, 0, 1, 0.5))
> abline(v=mean(s2), col="lightblue", lwd=3)
> 
> diff <- (mean(s1)-mean(s2))
> diff
[1] -9.80017
> se.ts 
[1] 1.25694
> diff/se.ts
[1] -7.79685
> t.out$statistic
       t 
-7.79685 
>

…………………………..

7

> ####
> # repeated measure t-test
> # we can use the above case 
> # pop paramter unknown
> # two consecutive measurement 
> # for the same sample 
> 
> t1 <- s1
> t2 <- s2
> mean(t1)
[1] 100.3577
> mean(t2)
[1] 110.1579
> diff.s <- t1 - t2
> head(diff.s)
[1]  -8.588426 -21.283258 -12.958503  -7.221480  -9.284982 -22.907759
> t.cal.rm <- mean(diff.s)/se(diff.s)
> t.cal.rm
[1] -8.215406
> p.val.rm <- pt(abs(t.cal.rm), 
+                length(s1)-1, 
+                lower.tail = F) * 2
> p.val.rm
[1] 8.276575e-13
> t.test(s1, s2, paired = T)

	Paired t-test

data:  s1 and s2
t = -8.2154, df = 99, p-value = 8.277e-13
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -12.167145  -7.433195
sample estimates:
mean difference 
       -9.80017 

>

…………………………..

8 t-test and anova

> # 2 샘플 히스토그램을 이용해서
> # anova 설명하기 
> s.all <- c(s1,s2)
> mean(s.all) # 두 집단을 합친 
[1] 104.7682
> # 종속변인의 평균 (아래 히스토
> # 그램에서 검정색).
> hist(s1, col='grey', breaks=30, xlim=c(50, 150),
+      main = "histogram of s1, s2")
> hist(s2, col='yellow', breaks=30, add=TRUE)
> abline(v=c(mean(s.all)), 
+        col=c("black"), lwd=3)
> abline(v=c(mean(s1), mean(s2)), 
+        col=c("green", "red"), lwd=2)
>

……………………………….

9

> comb <- data.frame(s1,s2)
> dat <- stack(comb)
> head(dat)
     values ind
1 106.26706  s1
2 101.89180  s1
3  98.64593  s1
4  93.82977  s1
5  80.35249  s1
6 100.47300  s1
> tail(dat)
       values ind
195 111.33398  s2
196 115.99752  s2
197 109.85412  s2
198 126.80207  s2
199  99.13395  s2
200 130.01417  s2
>

……………………………….

10

> m.tot <- mean(s.all)
> m.s1 <- mean(s1)
> m.s2 <- mean(s2)
> 
> ss.tot <- ss(s.all)
> bet.s1 <- (m.tot - m.s1)^2 * length(s1)
> bet.s2 <- (m.tot - m.s2)^2 * length(s2)
> ss.bet <- bet.s1 + bet.s2
> ss.s1 <- ss(s1)
> ss.s2 <- ss(s2)
> ss.wit <- ss.s1+ss.s2
> 
> ss.tot
[1] 25203.89
> ss.bet
[1] 4219.463
> ss.wit
[1] 20984.43
> ss.bet+ss.wit
[1] 25203.89
> 
> df.tot <- length(s.all) - 1
> df.bet <- nlevels(dat$ind) - 1
> df.s1 <- length(s1)-1
> df.s2 <- length(s2)-1
> df.wit <- df.s1 + df.s2
> 
> df.tot
[1] 199
> df.bet
[1] 1
> df.wit
[1] 198
> df.bet+df.wit
[1] 199
>

………………………..

ss.between 은 두개의 집단과 그 집단의 평균으로 이루어진 분산에서의 ss값을 말한다.
그림에서 녹색선 위에 s1의 원소들이 모여있고
붉은색 선위에 s2원소들이 모여 있다고치면
이 분산은 그룹간 분산이 (between group variance) 된다.
이를 구하기 위해서 ss.bet의 공식을 사용한다.
ss.within의 경우에는 간단히 s1과 s2 집단의 ss값을 구하는 것으로
스크립트 초반에 언급된 ss값을 이용해서 구한후 더한다.

df.between은 그룹의 숫자에서 1을 뺀 숫자
df.within은 각 그룹내의 구성원에서 1을 뺀 후, 모두 더한 숫자이다
df.total은 전체 구성원에서 1을 빼거나, df.bet + df.wit 를 더한 숫자

11

> ss.tot/df.tot
[1] 126.6527
> ms.tot <- ss.tot/df.tot
> 
> ms.bet <- ss.bet / df.bet
> ms.wit <- ss.wit / df.wit
> 
> f.cal <- ms.bet / ms.wit
> f.cal
[1] 39.81302
> pf(f.cal, df.bet, df.wit, lower.tail = F)
[1] 1.792613e-09
> 
> f.test <-  aov(dat$values~ dat$ind, data = dat)
> sum.f.test <- summary(f.test)
> sum.f.test
             Df Sum Sq Mean Sq F value   Pr(>F)    
dat$ind       1   4219    4219   39.81 1.79e-09 ***
Residuals   198  20984     106                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 
> 
> sum.f.test[[1]][1,4]
[1] 39.81302
> sum.f.test[[1]][1,5]
[1] 1.792613e-09
> sqrt(f.cal)
[1] 6.309756
> t.cal.ts
[1] -6.309756
> 
> # the above is anova after all. 
>

………………………..

위에서 구한 ss 값들을 가지고 분산값을 구할 수 있다 (ms = mean square = variance)
ms.between은 ss.bet/df.bet 값을 말하는 것으로 그룹이 나누어짐으로써 구할 수 있었던 분산이다. 이 부분은 그룹 때문에 생긴 (treatment때문에 생긴) 분산이다.
ms.within은 ss.wit/df.wit 값을 말하는 것으로 그룹의 구성 때문에 구할 수 있었던 ss.between 를 제외한 나머지 ss값을 df.wit값으로 나누어준 값을 말한다. 이 부분이 random 파트이다.
이 둘의 비율을 F값이라고 하고, 이는 기본적으로
group difference 를 random difference 로 나눈 값을 말하고 이는
t-test의 difference/random error와 같은 형태를 갖는다

따라서, 분산을 이용해서 구한 F값은 표준편차를 이용해서 구한 t값의 제곱값을 갖게 된다.

12

> m1 <- lm(dat$values~dat$ind, data = dat)
> sum.m1 <- summary(m1)
> sum.m1

Call:
lm(formula = dat$values ~ dat$ind, data = dat)

Residuals:
     Min       1Q   Median       3Q      Max 
-31.4177  -5.7058   0.4976   6.2952  29.2586 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  100.175      1.029   97.31  < 2e-16 ***
dat$inds2      9.186      1.456    6.31 1.79e-09 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 10.29 on 198 degrees of freedom
Multiple R-squared:  0.1674,	Adjusted R-squared:  0.1632 
F-statistic: 39.81 on 1 and 198 DF,  p-value: 1.793e-09

> 
> sum.m1$r.square
[1] 0.1674131
> ss.bet # 독립변인인 s1, s2의 그룹
[1] 4219.463
> # 구분으로 설명된 ss.tot 중의 일부
> ss.tot # y 전체의 uncertainty
[1] 25203.89
> ss.bet/ss.tot
[1] 0.1674131
> 
> sum.m1$fstatistic[1]
   value 
39.81302 
> ms.bet/ms.wit
[1] 39.81302
> 
>

…………………………..

ss.tot 은 s1그룹과 s2그룹의 값을 한줄에 배열하여 구하는 종속변인의 (dat$values) ss값을 말한다. 즉, 독립변이 없을 때의 종속변인의 uncertainty를 말한다.
ss.bet은 독립변인이 고려됨으로써 설명된 종속부분의 일부를 말한다.
ss.tot = ss.bet + ss.wit
total uncertainty (a) = treatment effect (b) + random effect
b/a를 R square값이라고 부른다.

Table of Contents

t-test summing up

t-test summing up output

1

2

3

4

5

6

7

8 t-test and anova

9

10

11

12