mean X를 중심으로 x값들을 구해서 (x-v)에 사용하는 경우
#library(ggplot2)
#library(ggpmisc)
rm(list=ls())
# rnorm 펑션을 변형한 펑션으로
# mean값과 sd값을 같는 n개의 샘플원소를
# 구한다. (샘플의 평균과 표준편차가
# 정확히 원하는 값이 되도록 함)
rnorm2 <- function(n,mean,sd){
mean+sd*scale(rnorm(n))
}
# set.seed(191)
nx <- 1000
mx <- 50
sdx <- mx * 0.1
sdx # 5
x <- rnorm2(nx, mx, sdx)
# x <- rnorm2(1000, 50, 5) 와 동일
mean(x)
sd(x)
length(x)
hist(x)
x.span <- seq(from = mean(x)-3*sd(x),
to = mean(x)+3*sd(x),
by = .1)
residuals <- function(x, v) {
return(x - v)
}
# sum of square residual 값을
# 구하는 펑션
ssr <- function(x, v) {
residuals <- (x - v)
return(sum(residuals^2))
}
# mean square residual 값을
# 구하는 펑션 (mean square
# residual = variance)
msr <- function(x, v) {
residuals <- (x - v)
# return((sum(residuals^2))/(length(x)-1))
return((mean(residuals^2)))
}
ssrs <- c() # sum of square residuals
msrs <- c() # mean square residuals = variance
vs <- c() # the value of v in (x - v)
x.span
# x.span의 값들을 v값으로 삼아
# sum(x-x.span)^2 처럼 구하면
# SS값을 구한 것이 된다.
# 우리가 배운 SS값은 x.span의
# 값으로 샘플의 평균을 사용했을 때의
# residual 값이다.
# x.span은 샘플의 평균을 중심으로
# 여러가지 값을 사용하는 것을
# 가정한다.
for (i in x.span) {
res.x <- residuals(x,i)
# srs.x <- sum(res.x)
ssr.x <- ssr(x,i)
msr.x <- msr(x,i)
# srs <- append(srs, srs.x)
ssrs <- append(ssrs, ssr.x)
msrs <- append(msrs, msr.x)
vs <- append(vs, i)
}
# 아래 plot은 SS값들이나 (두번째는)
# MS값들을 v값이 변화함에 따라서
# (x.span의 범위에 따라서 변화)
# 어떻게 변화하는지 구한 것
plot(ssrs)
plot(msrs)
# 아래는 위에서 계산한 msr 값들을 저장한
# msrs값들 중에서 최소값이 되는 것을 찾은
# 것. 우리는 이것이 샘플의 평균임을 안다.
min(msrs)
# 최소값일 때의 위치 (msrs에서 몇번째인지)
min.pos.msrs <- which(msrs == min(msrs))
min.pos.msrs
# 그 위치에 해당하는 (그 때 사용된) v값
print(vs[min.pos.msrs])
다시 설명하면 위의 코드는 [sum(x-mean(x)^2 / n]을 (= ms값 혹은 분산값임) 구하는 식에 mean(x)대신에 다양한 x값을 넣어 본 것이다. 그리고, 이 때 ms값 중에서 최소값이 되는 지점을 찾아서 이 때 사용된 v값을 (mean(x)대신에 사용된) 알아 본것이다. 이 v값이 mean(x)이 되는 것을 확인하여 mean(x)값으로 빼서 구한 SS값이 가장 작은 ms값을 (혹은 SS값을) 갖는다는 것을 보여준다.
리소스를 많이 사용하지 않고 msr값이 최소가 되는 v값을 찾는 방법
위 방법의 단점은 x.span의 값을 길게 나열하여 한번씩 넣어서 msr값을 구하여 최소값을 보는데 리소스를 너무 사용한다는 것이다.
아래는 그 단점을 극복하는 방법이다.
# the above no gradient
gradient <- function(x, v){
residuals = x - v
# y = (sum(x-v)^2)/n 혹은 (mean(x-v)^2)
# 의 식이 ms값을 구하는 식인데
# 이를 v에 대해서 미분하면 chain rule을 써야 한다
# 자세한 것은 http://commres.net/wiki/estimated_standard_deviation
# 문서 중에 미분 부분 참조
# dy/dv = ( 2(x-v)*-1 ) / n chain rule
# dy/dv = -2 (x-v) / n = -2 (mean(residual))
dx = -2 * mean(residuals)
# return(list("ds" = dx))
return(dx)
} # function returns ds value
>
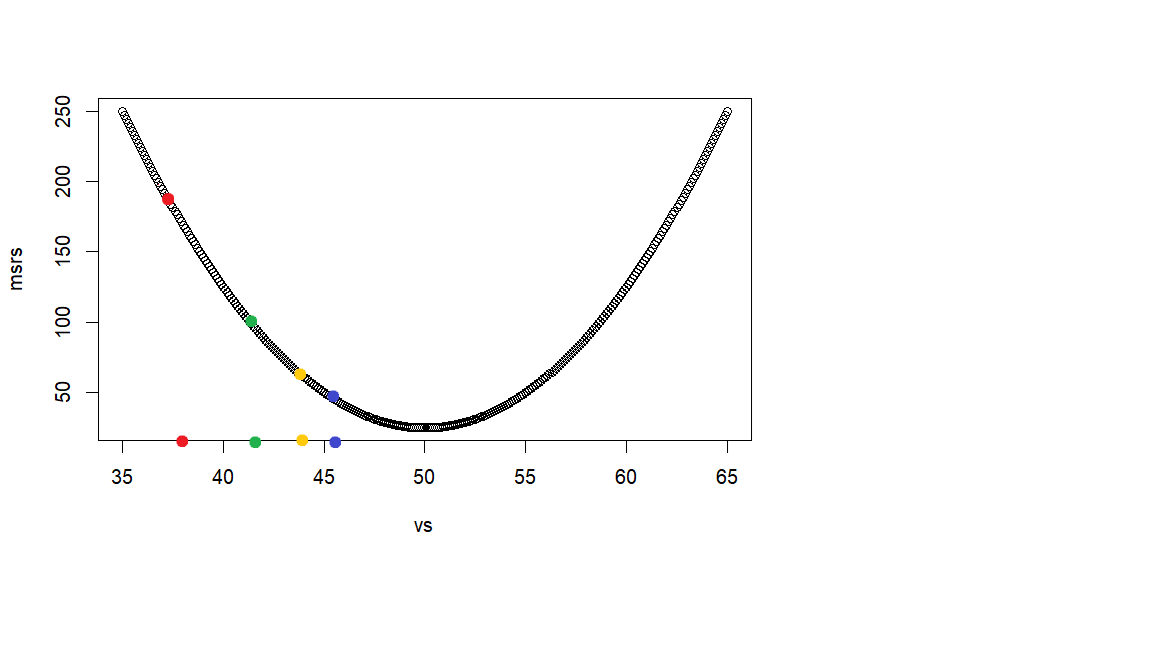
이후 일련의 코드의 목적은 v값이 최소값이 되는 지점을 자동적으로 찾아보려는 것이다. 이것을 위해서 우선 v값으로 사용할 첫 점수를 랜덤하게 구한 후 (아래 그래프에서 빨간색 지점), 자동적으로 그 다음 v 점수를 찾고 (녹색지점), 그 다음 v 점수를 찾고 (황금색 지점), . . . 이런 과정을 계속하면서 각 v 점수에서의 msr값을 구해서 이에 해당하는 v값을 찾아 보려고 한다. 빨간색, 녹색, 황금색, . . . 이를 자동적으로 구하기 위해서 두가지 방법을 사용하는데 그 것이
- gradient function과
- learning_rate 값이다.
gradient 펑션은 dy/dv 의 연쇄 미분식인 (chain rules) -2(x-v) / n = -2 mean(res) 값을 구하는 것이다. 이렇게 구한 값에 learning_rate값을 곱한후, 이것을 먼저 사용한 v값에서 (빨간색 지점) 빼 주어 다음 v값으로 (녹색지점) 사용하려고 한다. 이 녹색지점에서의 v값을 사용했을 때의 gradient값을 구한 후 다시 이값에 learning_rate인 0.1을 곱하여 그 다음 v값을 구하여 사용한다. 이렇게 구하는 v값들은 0.1씩 곱해주는 효과때문에 오른 쪽으로 옮겨가는 지점이 “점진적으로 줄어들게 되고” 이 지점이 msr의 최소값이 되는 지점으로 가게 된다.
residuals <- function(x, v) {
return(x - v)
}
ssr <- function(x, v) {
residuals <- (x - v)
return(sum(residuals^2))
}
msr <- function(x, v) {
residuals <- (x - v)
return((sum(residuals^2))/(length(x)-1))
# return(mean(residuals^2))
}
msr값을 구하기 위한 function
zx <- (x-mean(x))/sd(x) # pick one random v in (x-v) v <- rnorm(1) >
comment
- 랜덤하게 v값을 찾음
v ← rnorm(1) - 원래는 mean(x)값 근처의 값을 랜덤하게 골라야 하므로
v ← rnorm(1, mean(x), sd(x))와 같이 써야 하지만 (현재의 경우,rnorm(1, 50, 5)가 된다)- 그렇게 하질 않고 x 집합의 원소들을 표준점수화 한 후
zx ← (x-mean(x))/sd(x) - (이렇게 표준점수화 하면 x 변인의 평균이 0, 표준편차가 1 이 되는 집합으로 변한다)
v ← rnorm(1, 0, 1)로 구한다. 뒤의 인자인 0, 1 은 default이모로 생략.- 이렇게 하는 이유는 혹시 나중에 다른 x집합에 똑같은 작업을 하더라도 그 집합의 평균과 표준편차를 사용하지 않고
- 단순히
rnorm(1)을 이용해서 찾으려고 하는 것이다.
# Train the model with scaled features learning.rate = 1e-1
comment
- 이 0.1은 gradient function으로 구한 해단 v값에 대한 y 기울기 값을 (미분값)
- 구한 후, 여기에 곱하기 위해서 지정한다.
msrs <- c()
vs <- c()
nlen <- 75
for (epoch in 1:nlen) {
residual <- residuals(zx, v)
msr.x <- msr(zx, v)
grad <- gradient(zx, v)
step.v <- grad * learning.rate #
v <- v - step.v # 그 다음 v값
vs <- append(vs, v) # v값 저장
}
tail(msrs)
tail(vs)
plot(msrs)
plot(vs)
comment
# scaled vs # 변화하는 v 값들의 집합 vs.orig <- (vs*sd(x))+mean(x) vs.orig # 마지막 v값이 최소값에 근접한 값 v v.orig <- (v*sd(x))+mean(x) v.orig
comment