This is an old revision of the document!

using discrete probability distributions

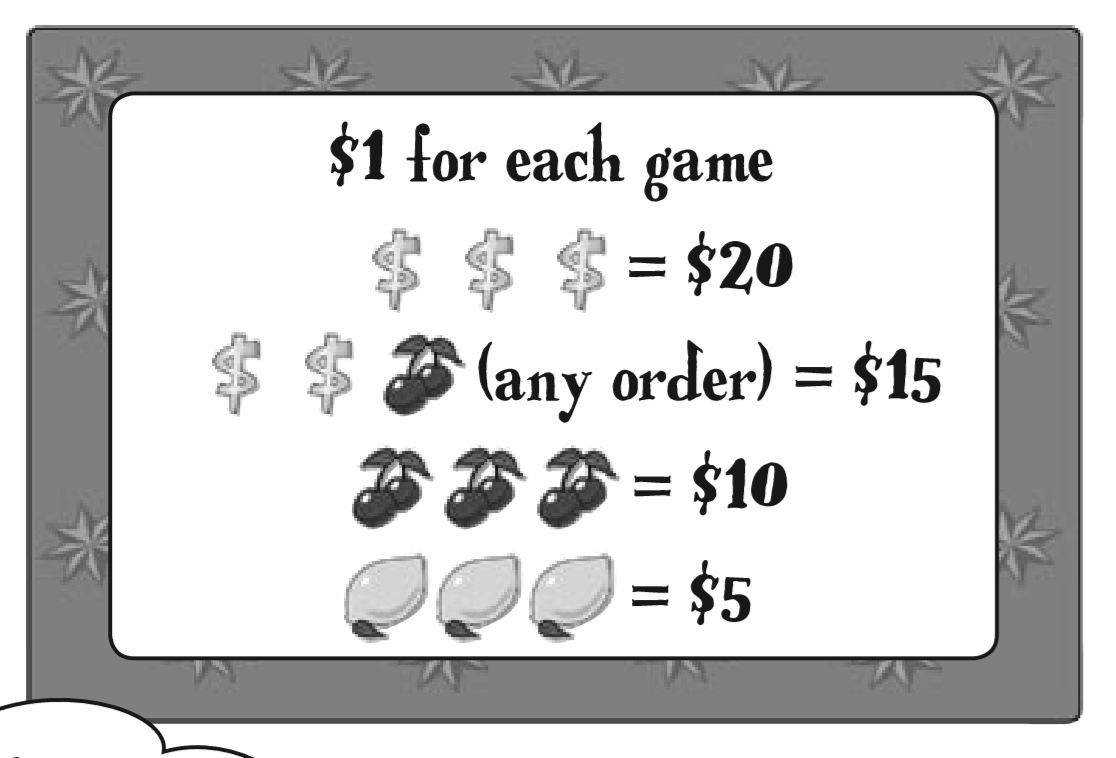
Dollar(D)	Cherry(C)	Lemon(L)	Other(O)
0.1	0.2	0.2	0.5

Probability of DDD
Probability of DDC (any order)
Probability of L
Probability of C
Probability of losing

P(D,D,D) = P(D) * P(D) * P(D)
- 0.1 x 0.1 x 0.1 = 0.001 = 1/1000

P(D,D,C) + P(D,C,D) + P(C,D,D)
- (0.1 * 0.1 * 0.2) + (0.1 * 0.2 * 0.1) + (0.2 * 0.1 * 0.1) = 6/1000

P(L,L,L) = P(L) + P(L) + P(L)
- .2 * .2 * .2 = .008 = 8/1000

P(C,C,C) = P(C) + P(C) + P(C)
- .2 * .2 * .2 = .008 = 8/1000

for nothing
- 1 - (1/1000 + 6/1000 + 8/1000 + 8/1000) = 1- 23/1000 = 977/1000

Prob. distribution

Combination	None	Lemons	Cherries	Dollars/cherry	Dollars
Probability	0.977	0.008	0.008	0.006	0.001

Combination	None	Lemons	Cherries	Dollars/cherry	Dollars
Gain	-1 dollar	4 dollar	9 dollar	14 dollar	19 dollar
Probability	0.977	0.008	0.008	0.006	0.001

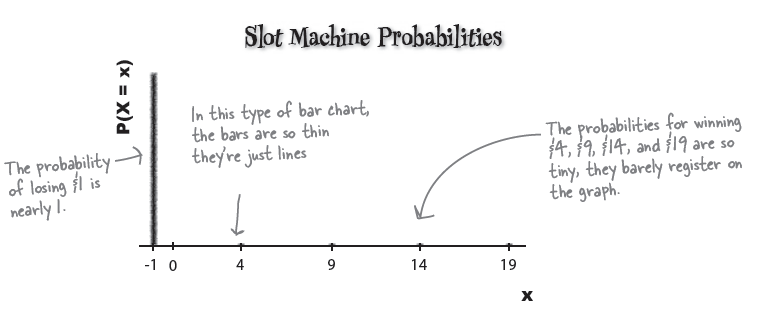
Combination	None	Lemons	Cherries	Dollars/cherry	Dollars
x	-1	4	9	14	19
P(X=x)	0.977	0.008	0.008	0.006	0.001

Expectation gives you . . .

$$ E(X) = \sum{k * P(X=x)} $$

Combination	None	Lemons	Cherries	Dollars/cherry	Dollars
k	-1	4	9	14	19
P(X=x)	0.977	0.008	0.008	0.006	0.001
E(X)	-0.977	4*0.008	9**0.008	14*0.006	19*0.001

$$E(X) = -0.77$$

k <- c(-1,4,9,14,19)
Px <- c(.977,.008,.008,.006,.001)
k*Px
sum(k*Px)
exp <- sum(k*Px)
exp

> k <- c(-1,4,9,14,19)
> Px <- c(.977,.008,.008,.006,.001)
> k*Px
[1] -0.977  0.032  0.072  0.084  0.019
> sum(k*Px)
[1] -0.77
> exp <- sum(k*Px)
> exp 
[1] -0.77

Variances and probability distributions

$$E(X-\mu)^2 = \sum{(x-\mu)^2}*P(X=x) $$

$$\mu = -.77 $$

a <- c(-1,4,9,14,19)
b <- c(.977,.008,.008,.006,.001)
a*b
sum(a*b)
mu <- sum(a*b)
a-mu
(a-mu)^2
((a-mu)^2)*b
sum(((a-mu)^2)*b)
varx <- sum(((a-mu)^2)*b)

> a <- c(-1,4,9,14,19)
> b <- c(.977,.008,.008,.006,.001)
> a*b
[1] -0.977  0.032  0.072  0.084  0.019
> sum(a*b)
[1] -0.77
varx
> mu <- sum(a*b)
> a-mu
[1] -0.23  4.77  9.77 14.77 19.77
> (a-mu)^2
[1]   0.0529  22.7529  95.4529 218.1529 390.8529
> ((a-mu)^2)*b
[1] 0.0516833 0.1820232 0.7636232 1.3089174 0.3908529
> sum(((a-mu)^2)*b)
[1] 2.6971
> varx <- sum(((a-mu)^2)*b)
> varx
[1] 2.6971

Var(X) = E(X - μ)^2 * P(X=x) 
= (-1 + 0.77)^2 × 0.977 + (4 + 0.77)^2 × 0.008 
  + (9 + 0.77)^2 × 0.008 + (14 + 0.77)^2 × 0.006 
  + (19 + 0.77)^2 × 0.001
= (-0.23)^2 × 0.977 + 4.772 × 0.008 + 9.772 × 0.008 
  + 14.772 × 0.006 + 19.772 × 0.001
= 0.0516833 + 0.1820232 + 0.7636232 
  + 1.3089174 + 0.3908529
= 2.6971

Standard deviation

\begin{eqnarray*} \text{s} & = & \sqrt{s^2} \\ & = & \sqrt{2.6971} \end{eqnarray*}

> sqrt(varx)
[1] 1.642285

e.g.

Here’s the probability distribution of a random variable X:

x	1	2	3	4	5
P(X = x)	0.1	0.25	0.35	0.2	0.1

$E(X)$ ?
$Var(X) $ ?

d <- c(1,2,3,4,5)
e <- c(.1,.25,.35,.2,.1)
de <- d*e
de
sum(de)

d <- c(1,2,3,4,5)
e <- c(.1,.25,.35,.2,.1)
de <- d*e
de
sum(de)

de.mu <- sum(de)
de1 <- (d-de.mu)^2
de1

de2 <- de1*e
de2

de.var <- sum(de2)
de.var

> d <- c(1,2,3,4,5)
> e <- c(.1,.25,.35,.2,.1)
> de <- d*e
> de
[1] 0.10 0.50 1.05 0.80 0.50
> sum(de)
[1] 2.95
> 
> de.mu <- sum(de)
> de1 <- (d-de.mu)^2
> de1
[1] 3.8025 0.9025 0.0025 1.1025 4.2025
> 
> de2 <- de1*e
> de2
[1] 0.380250 0.225625 0.000875 0.220500 0.420250
> 
> de.var <- sum(de2)
> de.var
[1] 1.2475
>

> d <- c(1,2,3,4,5)
> e <- c(.1,.25,.35,.2,.1)
> de <- d*2
> de
[1]  2  4  6  8 10
> de <- d*e
> de
[1] 0.10 0.50 1.05 0.80 0.50
> sum(de)
[1] 2.95
> de.mu <- sum(de)
> de1 <- (d-de.mu)^2
> de1
[1] 3.8025 0.9025 0.0025 1.1025 4.2025
> de2 <- de1*e
> de2
[1] 0.380250 0.225625 0.000875 0.220500 0.420250
> de.var <- sum(de2)
> de.var
[1] 1.2475
>

Fat Dan changed his prices

Another probability distribution.

Combination	None	Lemons	Cherries	Dollars/cherry	Dollars
y	-2	23	48	73	98
P(Y = y)	0.977	0.008	0.008	0.006	0.001

Original one

Combination	None	Lemons	Cherries	Dollars/cherry	Dollars
k	-1	4	9	14	19
P(X=x)	0.977	0.008	0.008	0.006	0.001

k <- c(-2,   23,   48,   73,   98)
j <- c(0.977,0.008,0.008,0.006,0.001)
k*j
sum(k*j)
kj.mu <- sum(k*j)
kj.mu

> k <- c(-2,   23,   48,   73,   98)
> j <- c(0.977,0.008,0.008,0.006,0.001)
> k*j
[1] -1.954  0.184  0.384  0.438  0.098
> sum(k*j)
[1] -0.85
> kj.mu <- sum(k*j)
> kj.mu
[1] -0.85

The expectation is slightly lower, so in the long term, we can expect to lose $ 0.85 each game. The variance is
much larger. This means that we stand to lose more money in the long term on this machine, but there’s less
certainty.
Do

kj.mu <- sum(k*j)
kj.var <- sum((k-kj.mu)^2*j)
kj.var

> kj.mu <- sum(k*j)
> kj.var <- sum((k-kj.mu)^2*j)
> kj.var
[1] 67.4275
>

Q: So expectation is a lot like the mean. Is there anything for probability distributions that's like the median or mode?
A: You can work out the most likely probability, which would be a bit like the mode, but you won't normally have to do this. When it comes to probability distributions, the measure that statisticians are most interested in is the expectation.

Q: Shouldn't the expectation be one of the values that X can take?
A: It doesn't have to be. Just as the mean of a set of values isn't necessarily the same as one of the values, the expectation of a probability distribution isn't necessarily one of the values X can take.

Q: Are the variance and standard deviation the same as we had before when we were dealing with values?
A: They're the same, except that this time we're dealing with probability distributions. The variance and standard deviation of a set of values are ways of measuring how far values are spread out from the mean. The variance and standard deviation of a probability distribution measure how the probabilities of particular values are dispersed.

Q: I find the concept of E(X - μ)2 confusing. Is it the same as finding E(X - μ) and then squaring the end result?
A: No, these are two different calculations. E(X - μ)2 means that you find the square of X - μ for each value of X, and then find the expectation of all the results. If you calculate E(X - μ) and then square the result, you'll get a completely different answer. Technically speaking, you're working out E((X - μ)2), but it's not often written that way.

Q: So what's the difference between a slot machine with a low variance and one with a high variance?
A: A slot machine with a high variance means that there's a lot more variability in your overall winnings. The amount you could win overall is less predictable. In general, the smaller the variance is, the closer your average winnings per game are likely to be to the expectation. If you play on a slot machine with a larger variance, your overall winnings will be less reliable.

Pool puzzle

\begin{eqnarray*} X & = & (\text{original win}) - (\text{original cost}) \\ & = & (\text{original win}) - 1 \\ (\text{original win}) & = & X + 1 \\ \\ Y & = & 5 * (\text{original win}) - (\text{new cost}) \\ & = & 5 * (\text{X + 1}) - 2 \\ & = & 5 * X + 5 - 2 \\ & = & 5 * X + 3 \\ \end{eqnarray*}

E(X) = -.77 and E(Y) = -.85. What is 5 * E(X) + 3?

$ 5 * E(X) = -3.85 $
$ 5 * E(X) + 3 = -0.85 $
$ E(Y) = 5 * E(X) + 3 $

$ 5 * Var(X) = 13.4855 $
$ 5^2 * Var(X) = 67.4275 $
$ Var(Y) = 5^2 * Var(X) $

\begin{eqnarray*} E(aX + b) & = & a \cdot E(X) + b \\ Var(aX + b) & = & a^{2} \cdot Var(X) \\ E(X + Y) & = & E(X) + E(Y) \\ Var(X + Y) & = & Var(X) + Var(Y) \\ \end{eqnarray*}

\begin{eqnarray*} E(X1 + X2 + \ldots Xn) & = & nE(X) \\ Var(X1 + X2 + \ldots Xn) & = & nVar(X) \\ \end{eqnarray*}

\begin{eqnarray*} E(X + Y) & = & E(X) + E(Y) \\ Var(X + Y) & = & Var(X) + Var(Y) \\ E(X - Y) & = & E(X) - E(Y) \\ Var(X - Y) & = & Var(X) + Var(Y) \\ E(aX + bY) & = & aE(X) + bE(Y) \\ Var(aX + bY) & = & a^{2}Var(X) + b^{2}Var(Y) \\ E(aX - bY) & = & aE(X) - bE(Y) \\ Var(aX - bY) & = & a^{2}Var(X) + b^{2}Var(Y) \\ \end{eqnarray*}

A restaurant offers two menus, one for weekdays and the other for weekends. Each menu offers four set prices, and the probability distributions for the amount someone pays is as follows:

Weekday:
x	10	15	20	25
P(X = x)	0.2	0.5	0.2	0.1

Weekend:
y	15	20	25	30
P(Y = y)	0.15	0.6	0.2	0.05

Who would you expect to pay the restaurant most: a group of 20 eating at the weekend, or a group of 25 eating on a weekday?

x1 <- c(10,15,20,25) 
x1p <- c(.2,.5,.2,.1)
x2 <- c(15,20,25,30)
x2p <- c(.15,.6,.2,.05)
x1n <- 25
x2n <- 20

x1mu <- sum(x1*x1p)
x2mu <- sum(x2*x2p)

x1e <- x1mu*x1num
x2e <- x2mu*x2num

x1e
x2e

> x1e
[1] 400
> x2e
[1] 415
>

x2e will spend more.

e.g.

Sam likes to eat out at two restaurants. Restaurant A is generally more expensive than
restaurant B, but the food quality is generally much better.
Below you’ll find two probability distributions detailing how much Sam tends to spend at each
restaurant. As a general rule, what would you say is the difference in price between the two
restaurants? What’s the variance of this?

Restaurant A:
x	20	30	40	45
P(X = x)	0.3	0.4	0.2	0.1

Restaurant B:
y	10	15	18
P(Y = y)	0.2	0.6	0.2

x3 <- c(20,30,40,45)
x3p <- c(.3,.4,.2,.1)
x4 <- c(10,15,18)
x4p <- c(.2,.6,.2)

x3e <- sum(x3*x3p)
x4e <- sum(x4*x4p)

x3e
x4e
## difference in price between the two
x3e-x4e


x3var <- sum(((x3-x3e)^2)*x3p)
x4var <- sum(((x4-x4e)^2)*x4p)

x3var
x4var
## difference in variance between the two
## == variance range 
x3var+x4var

> x3 <- c(20,30,40,45)
> x3p <- c(.3,.4,.2,.1)
> x4 <- c(10,15,18)
> x4p <- c(.2,.6,.2)
> 
> x3e <- sum(x3*x3p)
> x4e <- sum(x4*x4p)
> 
> x3e
[1] 30.5
> x4e
[1] 14.6
> ## difference in price between the two
> x3e-x4e
[1] 15.9
> 
> 
> x3var <- sum(((x3-x3e)^2)*x3p)
> x4var <- sum(((x4-x4e)^2)*x4p)
> 
> x3var
[1] 72.25
> x4var
[1] 6.64
> ## difference in variance between the two
> ## == variance range 
> x3var+x4var
[1] 78.89

e.g.

E(aX + b)	$aE(X) + b$
Var(aX + b)	$a^{2}Var(X)$
E(X)	$\sum{x} \cdot P(X=x) $
E(f(X))	$\sum{f(X)} \cdot P(X=x)$
Var(aX - bY)	$a^{2}Var(X) + b^{2}Var(Y)$ see 1
Var(X)	$E(X-\mu)^{2} = E(X^{2})-\mu^{2}$
E(aX - bY)	$aE(X)-bE(Y)$
E(X1 + X2 + X3)	$3E(X)$
Var(X1 + X2 + X3)	$3Var(X)$
E(X2)	$\sum{X^{2}}\cdot P(X=x)$
Var(aX - b)	$a^{2}Var(X)$

\begin{eqnarray*} Var(aX - bY) & = & Var(aX + -bY) \\ & = & Var(aX) + Var(-bY) \\ & = & a^{2}Var(X) + b^{2}Var(Y) \end{eqnarray*}

COMMunication
RESearch.NET

Table of Contents

using discrete probability distributions

Prob. distribution

Expectation gives you . . .

Variances and probability distributions

Standard deviation

e.g.

Fat Dan changed his prices

e.g.

e.g.