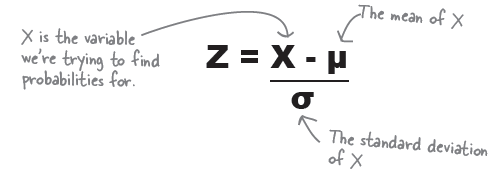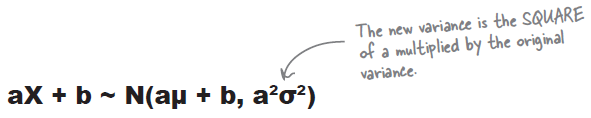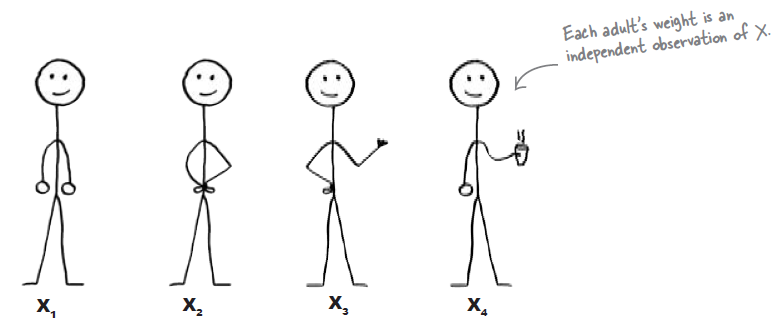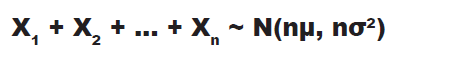Table of Contents
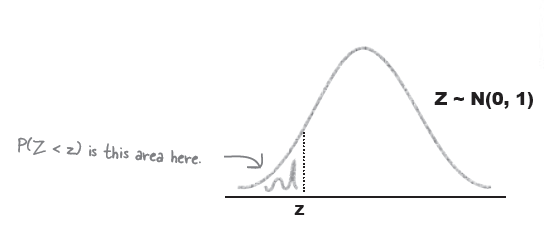
Using the normal distribution
7장까지는 이산데이터에 (discrete data) 기초한 확률을 살펴보았다. 이산데이터란 정확한 가치에 기초한 것을 말하는 것으로 룰렛에서 이기는 횟수, 성공하는 횟수, 방문하는 횟수, 등등을 말한다. 비록 이는 종류로 측정된 것이 아닌 수치적데이터라고 할 수는 있지만, 연속적인 (continuous) 데이터와는 다른 성격을 갖는다. 끈의 길이나, IQ 점수, 성적(GPA), 등등은 단위적인 측정이 (discrete) 아닌, 정밀한 수치를 조밀하게 등분하여 측정하는 것을 말한다.
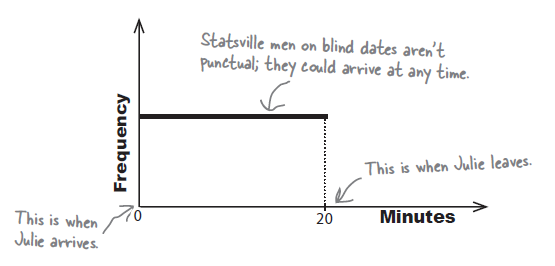
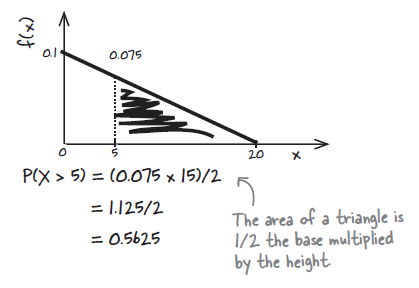
20분 동안만 기다리고 그 직후 떠나버리는 줄리의 상황에서 20분 동안의 시간 중에서 5분이상을 기달릴 확률을 구하는 것은 이산데이터와는 다른 성격을 갖는다. 아래는 베팅에서의 상금을 기초로 각 상황에 (discrete situation) 맞는 확률을 구하여 전체를 파악하는 것이지만, 시간의 경우는 이와 같은 방법을 수행할 수 없다.
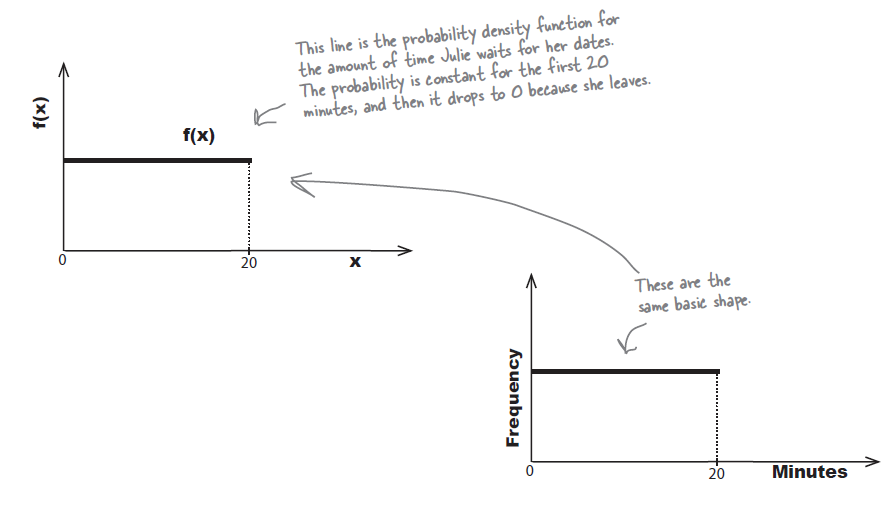
연속적인 데이터에는 확률밀도함수를 (probability density function) 사용할 수 있다.
대부분 확률 = 면적과 같이 생각할 수 있다.
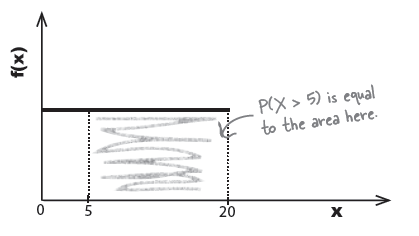
총 20 *1 의 면적 중에서 15 * 1의 면적이 P(X > 5)일 때의 확률이다. 이는
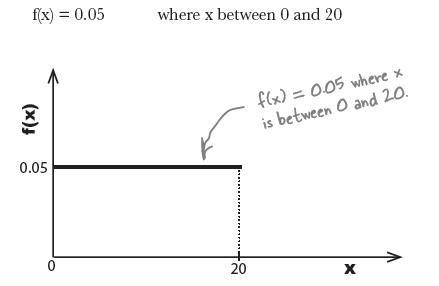
\begin{eqnarray*} 1 & = & 20 * \text{height} \\ \text{height} & = & 1/20 \\ & = & 0.05 \end{eqnarray*}
따라서 전체 면적을 1로 보는 상황에서, 이 경우는 f(x) = 0.05 라는 공식의 함수를 갖는다.
이 경우에 $P(X > 5)$는
\begin{eqnarray*} P(X > 5) & = & (20 - 5) * 0.05 \\ & = & 0.75 \end{eqnarray*}
우리가 면적을 이용하는 이유는 x축의 모든 경우를 discrete하게 (이산적으로) 나타낼 수 없기 때문이다.
exercise
BE the probability density function
A bunch of probability density functions have lost track of their probabilities. Your job is to play like you’re the probability density function and work out the probability between the specified ranges. Draw a sketch if you think that will help.
1. f(x) = 0.05 where 0 < x < 20 Find P(X < 5)
2. f(x) = 1 where 0 < x < 1 Find P(X < 0.5)
3. f(x) = 1 where 0 < x < 1 Find P(X > 2)
4. f(x) = 0.1 – 0.005x where 0 < x < 20 Find P(X > 5)
Probability density function
연속형 데이터에서는, probability density functions 을 사용한다.
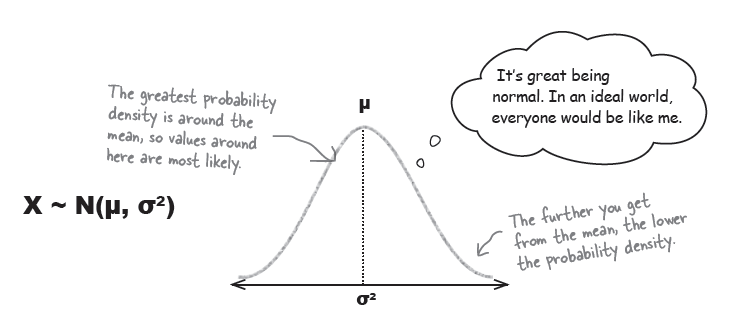
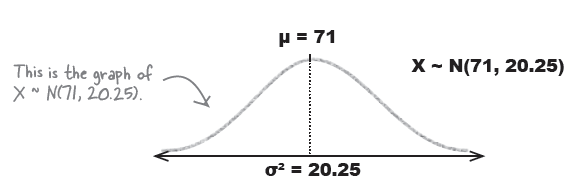
“키”와 같은 데이터 전체는 아래와 같은 분포곡선을 이용하여 표현한다.
주의: $X \sim N(\mu, \sigma^{2})$ 처럼 표현.
\begin{align*} \mu & = \text{mean} \\ \sigma^{2} & = \text{variance} \\ \sqrt{\sigma^{2}} & = \sigma \\ & = \text{standard deviation} \end{align*}
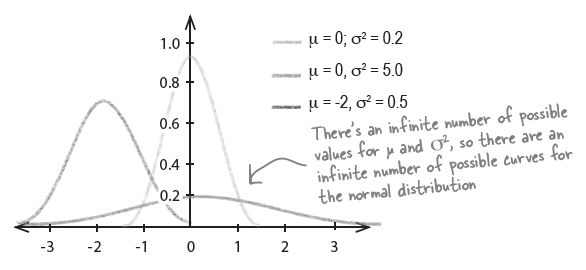
No matter how far you go out on the graph, the probability density never equals 0.
So how do we find normal probabilities?
평균이 0 이고 표준편차가 1일 Normal distribution 에서의 probabilities는 아래의 PDF 파일과 같이 구해 놓은 값이 있다
(R을 이용하지 않는다면). z table 링크
평균과 표준편차 값이 0, 1이 아닌 다른 값을 같는 분포는 0, 1 이 되도록 변환한 후에 probability를 구한다 (표준점수화).
e.g.,
$X \sim N(71, 20.25)$
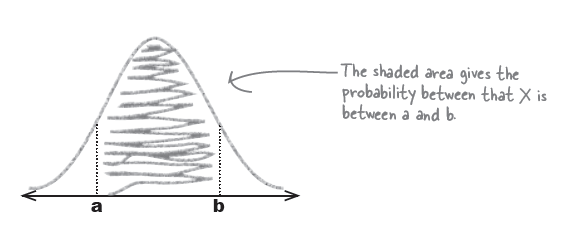
Julie's height = 64 inches 이므로, 아래의 면적에서 빗금친 부분을 구하면 된다.
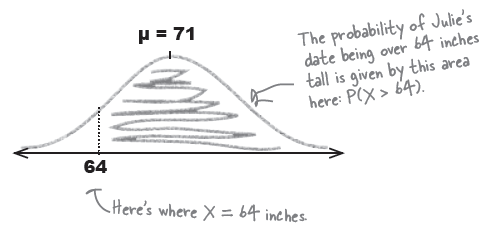
결론적으로, 이 면적을 알기 위해서 64 인치보다 큰 면적을 계산해 준 테이블을 참조하게 되는데, 이 방법의 단점은 모든 평균과 표준편차를 고려한 면적을 제시해 줄 수 있는 표를 만들어 둘 수는 없다. 따라서, Z ~ N(0, 1) 의 표만을 제시하고, 모든 데이터는 Z (표준화) 하여 살펴본다 (아래 그림 참조)
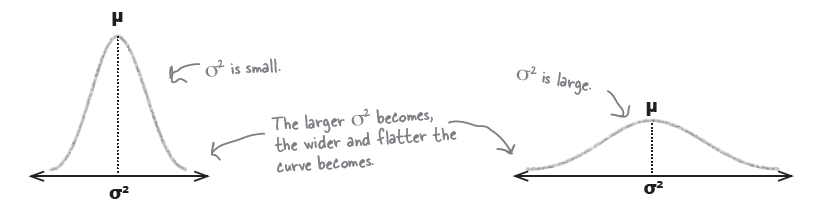
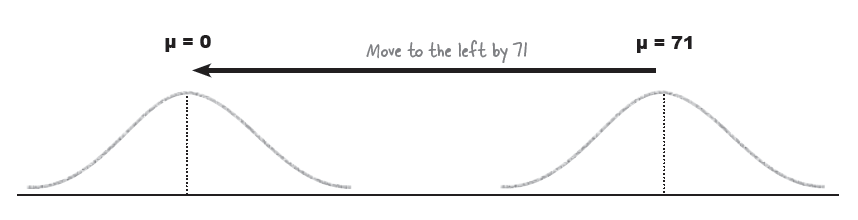
To standardize, first move the mean…
…then squash the width
그래프를 표준편차가 1이 되도록 찌부러뜨린다 (squash).
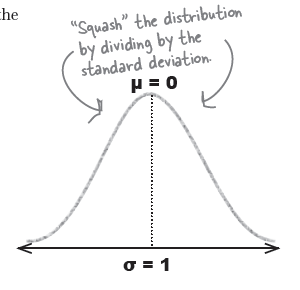
이를 위해서
\begin{eqnarray*} \displaystyle\frac {X - 71} {\sqrt{20.25}} & \sim & N(0, 1) \\ \displaystyle\frac {X - 71} {4.5} & \sim & N(0, 1) \end{eqnarray*}
이를 일반화하면
따라서, 이 데이터를 같이 변환하여 z 점수를 찾기 위해서는 (표준점수를 찾기 위해서는)
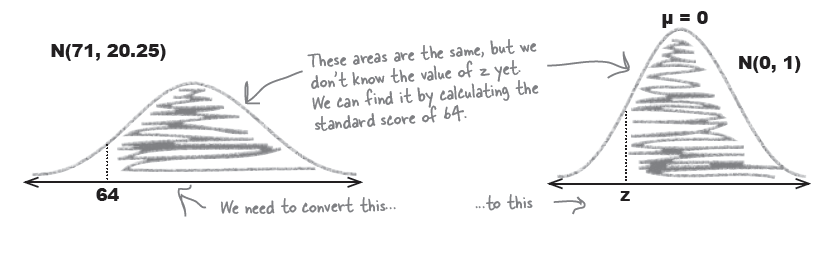
\begin{eqnarray*} z & = & \displaystyle \frac {x - \mu}{\sigma} \\ & = & \frac {64-71} {4.5} \\ & = & - 1.56 \end{eqnarray*}
따라서, 표준점수를 -1.56을 가지고 표준점수 테이블에서 -1.56보다 큰 부분의 면적을 구한것을 참조하면 된다.
> 1 - pnorm(-1.56) [1] 0.9406201 > pnorm(-1.56, lower.tail = FALSE) [1] 0.9406201 > pnorm(64, 71, sqrt(20.25), lower.tail = FALSE) [1] 0.9400931 >
exercise
1. N(10, 4), value 6
2. N(6.3, 9), value 0.3
3. N(2, 4). If the standard score is 0.5, what’s the value?
4. The standard score of value 20 is 2. If the variance is 16, what’s the mean?
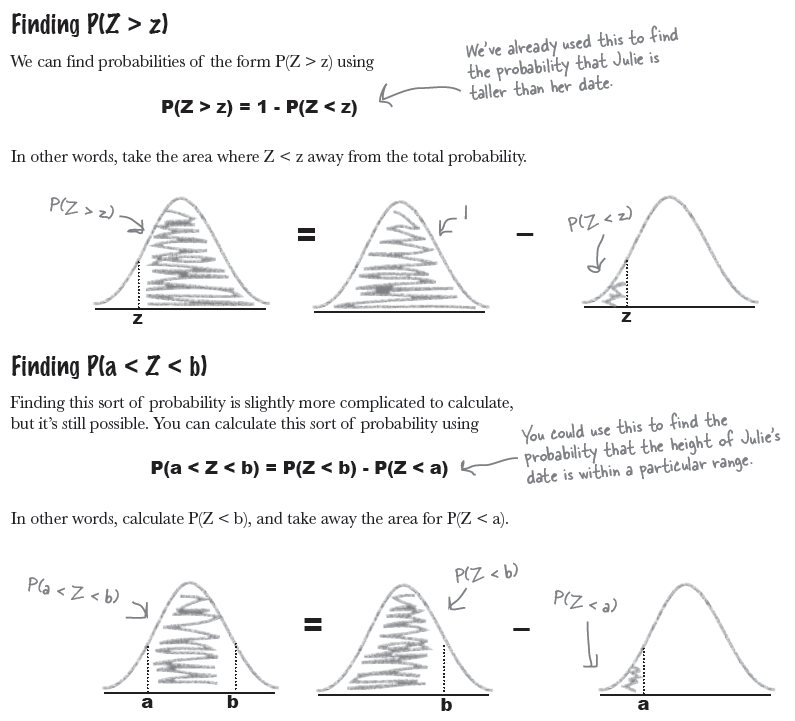
Step 3: Look up the probability in your handy table
해당 값은 (value) z 점수까지의 부분면적을 의미하므로, P(X > 1.56) 부분은 1에서 이 점수를 뺀 후에 구한다.
\begin{eqnarray*} P(Z > -1.56) & = & 1 - P(Z < -1.56) \\ & = & 1 - 0.0594 \\ & = & 0.9406 \end{eqnarray*}
That is, the probability that Julie’s date is taller than her is 0.9406.
> pnorm(0) [1] 0.5 > pnorm(-1) [1] 0.1586553 > pnorm(-1.56) [1] 0.05937994 > 1- pnorm(-1.56) > 1- pnorm(-1.56) [1] 0.9406201
Exercise
Julie with 5“ heels = 64 + 5 = 69
Remember X ~ N(71, 20.25)
mean = 71
variance = 20.25
sd = 4.5
z = (71-69)/4.5
z score = -0.44
\begin{eqnarray*} P(Z > -0.44) & = & 1 - P(Z < -0.44) \\ & = & 1 - 0.3300 \\ & = & 0.67 \end{eqnarray*}
> 1-pnorm(-0.44) [1] 0.6700314 >
rnorm
> set.seed(101) > rnorm(5) [1] -0.3260365 0.5524619 -0.6749438 0.2143595 0.3107692 > rnorm(5, mean=0, sd=1) [1] 1.1739663 0.6187899 -0.1127343 0.9170283 -0.2232594 >
> set.seed(101) > rnorm(5, mean=100, sd=10) [1] 96.73964 105.52462 93.25056 102.14359 103.10769 >
> set.seed(101) > s1 <- rnorm(100, mean=100, sd=10) > s1 [1] 96.73964 105.52462 93.25056 102.14359 103.10769 111.73966 106.18790 [8] 98.87266 109.17028 97.76741 105.26448 92.05156 114.27756 85.33180 [15] 97.63317 98.06662 91.50245 100.58465 91.82330 79.49692 98.36244 [22] 107.08522 97.32019 85.36078 107.44436 85.89610 104.67068 98.80680 [29] 104.67239 104.98136 108.94937 102.79152 110.07866 79.26894 111.89853 [36] 92.75626 101.67984 109.20335 83.28395 104.48469 104.82459 107.58214 [43] 76.80673 95.40495 88.94616 104.02928 105.68935 92.93917 97.09909 [50] 85.16122 88.49745 97.25529 105.77901 86.03097 107.49058 89.48813 [57] 101.65381 111.29809 111.73722 95.72137 97.40198 85.88827 93.58642 [64] 101.12458 104.22604 103.86835 93.12202 101.48902 99.42350 99.25177 [71] 115.09897 116.19937 111.53158 99.22396 81.81065 89.62555 103.02492 [78] 87.22054 101.38339 99.49016 118.52148 111.11675 94.88625 94.56119 [85] 82.71073 104.70750 100.05387 113.48046 107.24097 115.52549 113.25470 [92] 99.65735 96.38987 92.79835 102.82015 92.09474 95.55095 113.64993 [99] 104.97454 91.85604 > > mean(s1) [1] 99.62809 > sd(s1) [1] 9.34071 >
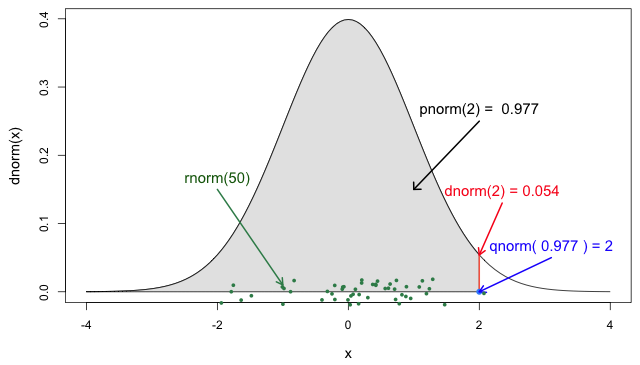
pnorm
qnorm
dnorm
> set.seed(101) > dnorm(0) [1] 0.3989423 > dnorm(0, mean=0, sd=1) [1] 0.3989423 > dnorm(0, mean=0, sd=5) [1] 0.07978846 >
pnorm
Mean <- 100 Sd <- 10 # X grid for non-standard normal distribution x <- seq(-4, 4, length = 100) * Sd + Mean # Density function f <- dnorm(x, Mean, Sd) plot(x, f, type = "l", lwd = 2, col = "blue", ylab = "", xlab = "Weight") abline(v = Mean) # Vertical line on the mean
# mean: mean of the Normal variable
# sd: standard deviation of the Normal variable
# lb: lower bound of the area
# ub: upper bound of the area
# acolor: color of the area
# ...: additional arguments to be passed to lines function
normal_area <- function(mean = 0, sd = 1, lb, ub, acolor = "lightgray", ...) {
x <- seq(mean - 3 * sd, mean + 3 * sd, length = 100)
if (missing(lb)) {
lb <- min(x)
}
if (missing(ub)) {
ub <- max(x)
}
x2 <- seq(lb, ub, length = 100)
plot(x, dnorm(x, mean, sd), type = "n", ylab = "")
y <- dnorm(x2, mean, sd)
polygon(c(lb, x2, ub), c(0, y, 0), col = acolor)
lines(x, dnorm(x, mean, sd), type = "l", ...)
}
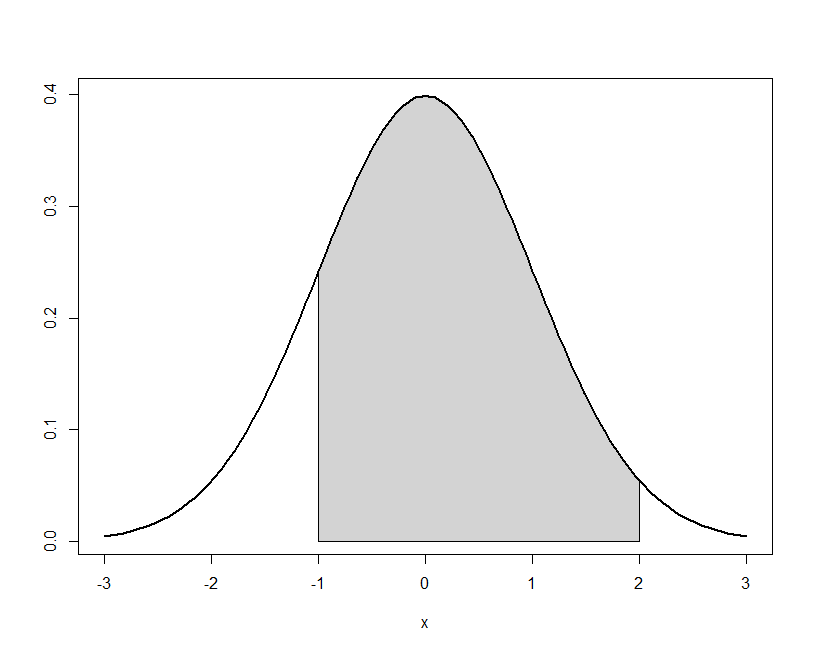
normal_area(mean = 0, sd = 1, lb = -1, ub = 2, lwd = 2)
pnorm(2) pnorm(-1) pnorm(2)-pnorm(-1) ar <- round(pnorm(2)-pnorm(-1),3)
> pnorm(2) [1] 0.9772499 > pnorm(-1) [1] 0.1586553 > pnorm(2)-pnorm(-1) [1] 0.8185946 > ar <- round(pnorm(2)-pnorm(-1),3) >
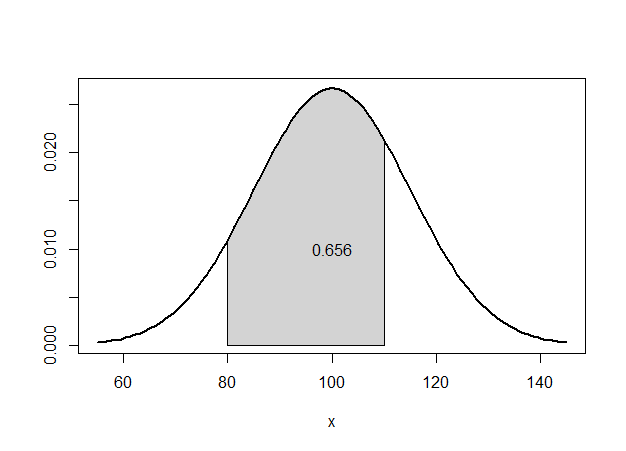
m.s <- 100 sd.s <- 15 lb <- 80 ub <- 110 normal_area(mean = m.s, sd = sd.s, lb = lb, ub = ub, lwd = 2) ar <- round(pnorm(ub, m.s, sd.s)-pnorm(lb, m.s, sd.s),3) text(m.s, .01, ar)
m.s <- 100 sd.s <- 15 lb <- m.s - sd.s ub <- m.s + sd.s normal_area(mean = m.s, sd = sd.s, lb = lb, ub = ub, lwd = 2) ar <- round(pnorm(ub, m.s, sd.s)-pnorm(lb, m.s, sd.s),3) text(m.s, .01, ar)
Headline
The Case of the Missing Parameters
Will at Manic Mango Games has a problem. He needs to give his boss the mean and standard deviation of the number of minutes people take to complete level one of their new game. This shouldn’t be difficult, but unfortunately a ferocious terrier has eaten the piece of paper he wrote them on.
Will only has three clues to help him.
- First of all, Will knows that the number of minutes people spend playing level one follows a normal distribution.
- Secondly, he knows that the probability of a player playing for less than 5 minutes is 0.0045.
- Finally, the probability of someone taking less than 15 minutes to complete level one is 0.9641.
How can Will find the mean and standard deviation?
조건 2에서, P(X < 5) = 0.0045 이므로, 이에 해당하는 z 점수는 -2.61.
조건 3에서는, P(X < 15) = 0.9641이므로, 이에 해당하는 z 점수는 1.8
> qnorm(0.0045) [1] -2.612054 > qnorm(0.9641) [1] 1.800384
\begin{eqnarray*} -2.61 & = & \frac {5-\mu}{\sigma} \\ 1.8 & = & \frac {15-\mu}{\sigma} \end{eqnarray*}
\begin{eqnarray} -2.61 \sigma & = & 5-\mu \\ 1.8 \sigma & = & 15-\mu \end{eqnarray}
위에서 (1) - (2)를 하면
\begin{eqnarray*}
(-2.61 - 1.8) \sigma & = & 5-\mu - 15 + \mu \\
-4.41 \sigma & = & -10 \\
\sigma & = & \frac {-10}{-4.41} \\
& = & 2.267574
\end{eqnarray*}
이를 (1)에 대입하면
\begin{eqnarray*}
1.8 * 2.267574 & = & 15-\mu \\
\mu & = & 15 - (1.8 * 2.267574) \\
& = & 10.91837
\end{eqnarray*}
따라서
\begin{eqnarray*}
\mu & = & 10.9184 \\
\sigma & = & 2.27
\end{eqnarray*}
Using the normal distribution II
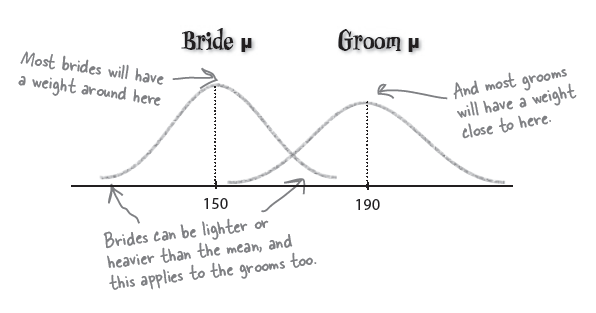
\begin{eqnarray*} \text{bride} \sim N(150, 400) \\ \text{groom} \sim N(190, 500) \end{eqnarray*}
For a roller coaster ride: should be under 380 lbs combined bride and groom.
이전 기대치 계산에서
\begin{eqnarray*}
E(X + Y) & = & E(X) + E(Y) \\
E(X - Y) & = & E(X) - E(Y) \\
Var(X + Y) & = & Var(X) + Var(Y) \\
Var(X - Y) & = & Var(X) + Var(Y)
\end{eqnarray*}
X + Y
\begin{eqnarray*} X \sim N(\mu_{X}, \sigma^{2}_{X}) \\ Y \sim N(\mu_{Y}, \sigma^{2}_{Y}) \end{eqnarray*}
\begin{eqnarray*} X + Y \sim N(\mu, \sigma^{2}) \end{eqnarray*}
\begin{eqnarray*} \mu & = & \mu_{X} + \mu_{Y} \\ \sigma^{2} & = & \sigma^{2}_{X} + \sigma^{2}_{Y} \end{eqnarray*}
즉, 전체 평균은 남자평균과 여자평균을 합한 것과 같고, 전체 분산값은 X 분산값과 Y 분산값을 더한 것이다.
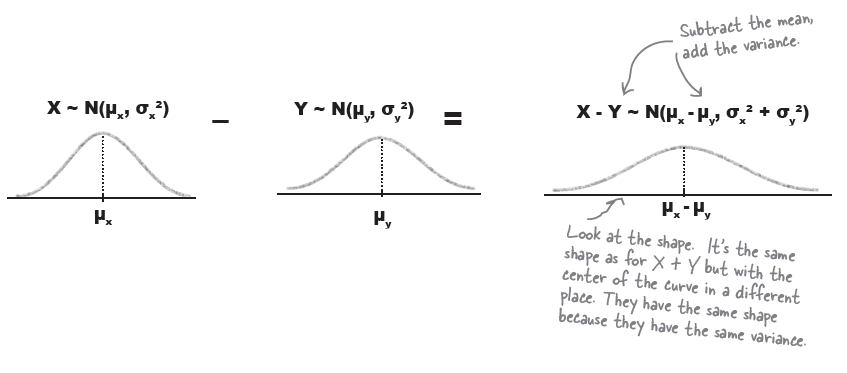
X - Y
\begin{eqnarray*} X \sim N(\mu_{X}, \sigma^{2}_{X}) \\ Y \sim N(\mu_{Y}, \sigma^{2}_{Y}) \end{eqnarray*}
\begin{eqnarray*} X - Y \sim N(\mu, \sigma^{2}) \end{eqnarray*}
\begin{eqnarray*} \mu & = & \mu_{X} - \mu_{Y} \\ \sigma^{2} & = & \sigma^{2}_{X} + \sigma^{2}_{Y} \end{eqnarray*}
즉, X - Y 분포의 평균은 남자평균과 여자평균의 차이와 같고, 전체 분산값은 X 분산값과 Y 분산값을 더한 것과 같다.
Find the probability that the combined weight of the bride and groom is less than 380 pounds using the following three steps.
X ~ N(150, 400), Y ~ N(190, 500)의 조건에서
$$X + Y \sim N(340, 900)$$
둘의 체중을 합한 값은 380 이므로,
\begin{eqnarray*} z & = & \frac {(X + Y) - \mu}{ \sigma } \\ & = & \frac {380 - 340}{ 30 } \\ & = & \frac {40}{30} \\ & = & 1.333 \end{eqnarray*}
P(X + Y < 380) 을 알아내기 위해서 z-table을 참조하거나 R을 이용한다.
> pnorm(1.333) [1] 0.9082409
pnorm in r: 표준점수에 해당하는 누적 퍼센티지 (Percentage)
> pnorm(1.333) [1] 0.9082409
참고로 R의 경우, 표준점수화는 r이 해 주므로, 아래와 같이 그 값을 구해도 된다.
> pnorm(380, 340, sqrt(900)) # 900은 variance이므로 sqrt값을 대입 # pnorm의 옵션은 (q, mean = 0, stdev = 1)이다. # 즉, mean, 0과 stdev, 1값에서 (표준점수에서) # q값에 해당하는 왼쪽부분의 percentile을 구하라 [1] 0.9087888
dnorm(x, mean = 0, sd = 1, log = FALSE) pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE) rnorm(n, mean = 0, sd = 1)
따라서
$$P(X + Y < 380) = 0.9082409 $$
exercise
Julie’s matchmaker is at it again. What's the probability that a man will be at least 5 inches taller than a woman? In Statsville, the height of men in inches is distributed as N(71, 20.25), and the height of women in inches is distributed as N(64, 16).
\begin{eqnarray*} M & \sim & N(71, 20.25) \\ F & \sim & N(64, 16) \end{eqnarray*}
probability that a man will be at least 5 inches taller than a woman? = “probability that a man will be at least 5 inches taller than (an average) woman” 이므로 $P(X > F + 5)$ 을 구하라는 문제.
\begin{align*}
P(X > F + 5) & = P(X - F > 5)
\end{align*}
그런데,
\begin{eqnarray*}
X - Y & \sim & N(\mu_{m} - \mu_{f}, \sigma^{2}_{m} + \sigma^{2}_{f}) \\
& \sim & N(7, 36.25)
\end{eqnarray*}
즉, 남성과 여성 평균의 차이로 이루어진 분포는 $X \sim N(7, 36.25)$ 를 따른다.
위에서 $\sigma$ 값은 $\sqrt{\sigma^2}$ 이므로 $6.02$
X - Y = 5점일 때의 표준점수는
\begin{eqnarray*}
z & = & \frac {(X-Y)-\mu}{\sigma} \\
& = & \frac {5-7}{6.02} \\
& = & -0.3322259
\end{eqnarray*}
따라서 정답은 1 - pnorm(-0.33) 인
> 1 - pnorm(-0.3322259, 0, 1) [1] 0.6301407 # 혹은 아래와 같이 직접 구한다. > 1 - pnorm(5, 7, sqrt(36.25)) [1] 0.6301241 # "1 -"를 사용하는 대신 lower.tail = FALSE 를 사용할 수도 있다. > pnorm(5, 7, sqrt(36.25), lower.tail = FALSE) [1] 0.6301241
Linear Transform
4인용 roller coaster의 지지하중 무게는 800 LBs 라고 한다. 그리고 Statsville 사람들의 평균 몸무게는 180, 분산은 625라고 할 수 있다. 네명을 합한 무게가 800 LBs 보다 작을 확률은 얼마나 될까?
The distribution of 4X is actually a linear transform of X. It’s a transformation of X in the form aX + b, where a is equal to 4, and b is equal to 0. This is exactly the same sort of transform as we encountered earlier with discrete probability distributions. Linear transforms describe underlying changes to the size of the values in the probability distribution. This means that 4X actually describes the weight of an individual adult whose weight has been multiplied by 4.
즉, transforamtion의 경우는 한 개인의 몸무게가 4배가 될 때를 의미하지 단순히 4명을 합하는 것을 의미하지는 않음. 전자의 경우에 distribution은 아래를 따른다.
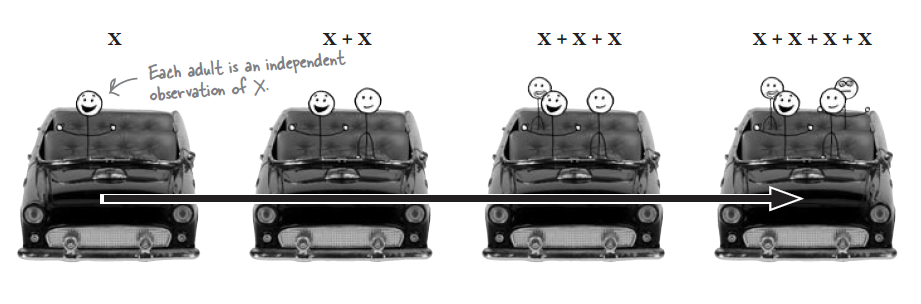
Independent Observation
Rather than transforming the weight of each adult, what we really need to figure out is the probability distribution for the combined weight of four separate adults. In other words, we need to work out the probability distribution of four independent observations of X.
즉, 개인이 하나씩 늘어 4명이 된다. 개인이 4X가 (X=몸무게) 되는 것이 아님.
각 개인의 몸무게는 독립적인 observation이다. 이 경우의 분포는 아래르 따른다.
Q: So what’s the difference between linear transforms and independent observations?
A: Linear transforms affect the underlying values in your probability distribution. As an example, if you have a length of rope of a particular length, then applying a linear transform affects the length of the rope. Independent observations have to do with the quantity of things you’re dealing with. As an example, if you have n independent observations of a piece of rope, then you’re talking about n pieces of rope. In general, if the quantity changes, you’re dealing with independent observations. If the underlying values change, then you’re dealing with a transform.
Q: Do I really have to know which is which? What difference does it make?
A: You have to know which is which because it make a difference in your probability calculations. You calculate the expectation for linear transforms and independent observations in the same way, but there’s a big difference in the way the variance is calculated. If you have n independent observations then the variance is n times the original. If you transform your probability distribution as aX + b, then your variance becomes a2 times the original.
Q: Can I have both independent observations and linear transforms in the same probability distribution?
A: Yes you can. To work out the probability distribution, just follow the basic rules for calculating expectation and variance. You use the same rules for both discrete and continuous probability distributions.
그러므로 앞의 문제에 대한 해답은:
$X_{1} + X_{2} + X_{3} + X_{4} \sim N(720, 2500)$ 로 표현할 수 있다.
$P(X_{1} + X_{2} + X_{3} + X_{4} < 800)$ 을 구하기 위해서는 800에 해당하는 표준점수를 구한 후, 누적 퍼센티지를 알아내면 된다.
\begin{eqnarray*} z & = & \frac {x-\mu}{\sigma} \\ & = & \frac {800-720}{50} \\ & = & \frac {80}{50} \\ & = & 1.6 \end{eqnarray*}
따라서, pnorm(1.6)의 점수인 0.9452007이 답.
> pnorm(1.6) [1] 0.9452007 # 혹은 > pnorm(800, 720, sqrt(2500), lower.tail = TRUE) [1] 0.9452007
Swivel chair again
Before going further:
So what’s the probability of getting 30 or more questions right out of 40? That will help us determine whether to keep playing, or walk away.
There are 40 questions, which means there are 40 trials.
The outcome of each trial can be a success or failure, and we want to find the probability of getting a certain number of successes.
In order to do this, we need to use the binomial distribution. We use n = 40, and as each question has four possible answers, p is 1/4 or 0.25..
If X is the number of questions we get right, then we want to find P(X > 30).
This means we have to calculate and add together the probabilities for P(X = 30) up to P(X = 40).
We can find the mean and variance using n, p and q, where q = 1 - p. The mean is equal to np, and the variance is equal to npq. This gives us a mean of 40 x 0.25 = 10, and a variance of 40 x 0.25 x 0.75 = 7.5.
> pbinom(29,40, 1/4, lower.tail = F) [1] 4.630881e-11
r에서 다음의 함수가 이항분포의 결과값을 구하는데 사용된다: dbinom, pbinom, qbinom, rbinom
# X ~ B(10, 0.2)의 분포를 따를 때, # X는 2일 때의 확률은? 즉, P(X=2)? dbinom(2, 10, 0.2) k <- c(0:50) # or k <- seq(0, 50, 1) b <- dbinom(k, 50, 0.2) plot(k,b, type = "l") b <- dbinom(k, 50, 0.6) plot(k,b, type = "l") k <- seq(0, 100, 1) b <- dbinom(k, 100, 0.6) plot(k, b, type = "l")
# X ~ B(10, 0.2)의 분포를 따를 때, # X는 2일 때의 확률은? 즉, P(X=2)? dbinom(2, 10, 0.2) k <- c(0:50) # or k <- seq(0, 50, 1) b <- dbinom(k, 50, 0.2) plot(k, b, type = "p") b <- dbinom(k, 50, 0.6) plot(k, b, type = "p") k <- seq(0, 100, 1) b <- dbinom(k, 100, 0.6) plot(k, b, type = "p")
위와 같은 식으로 문제의 해를 구한다고 하면
k <- seq(30, 40, 1) k b <- dbinom(k, 40, 0.25) b sum(b)
> k <- seq(30, 40, 1) > k [1] 30 31 32 33 34 35 36 37 38 39 40 > b <- dbinom(k, 40, 0.25) > b [1] 4.140329e-11 4.451967e-12 4.173719e-13 3.372702e-14 2.314599e-15 1.322628e-16 6.123279e-18 2.206587e-19 [9] 5.806808e-21 9.926167e-23 8.271806e-25 > sum(b) [1] 4.630881e-11 >
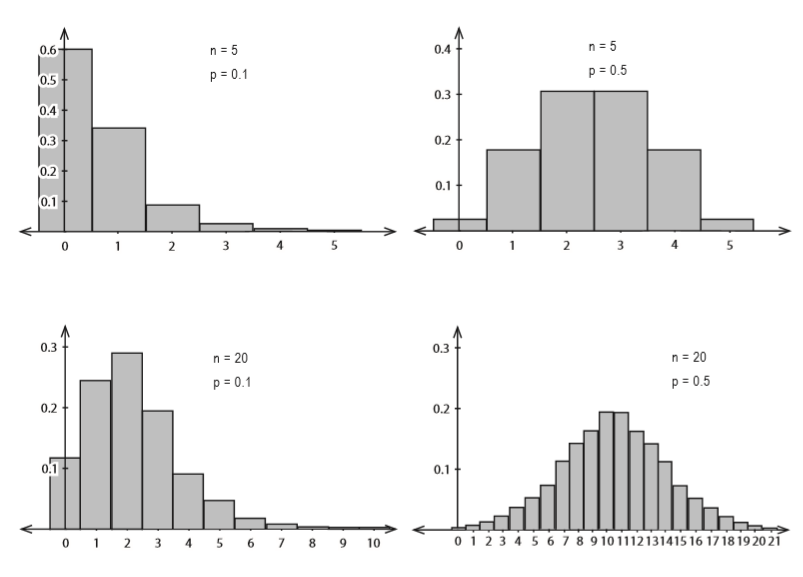
Normal distribution to the rescue
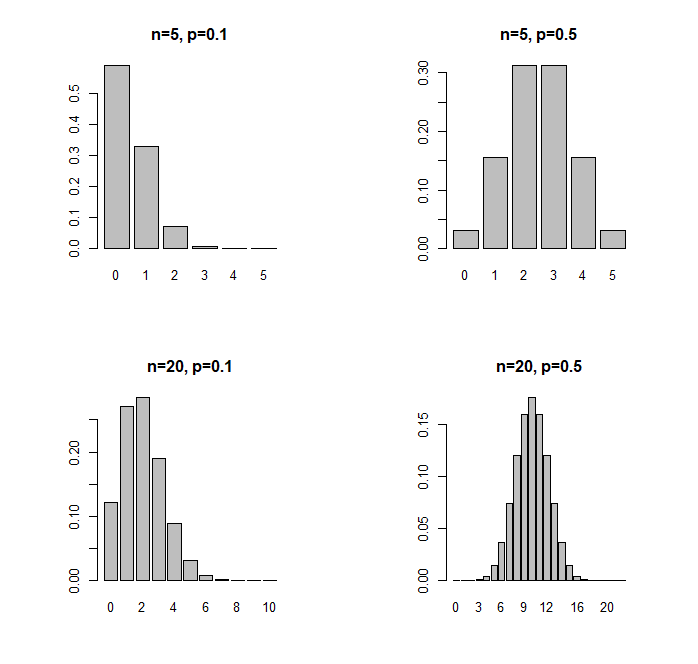
n20 <- 20 n5 <- 5 p1 <- .1 p5 <- .5 x <- c(0:30) a <- dbinom(x, n5, p1) c <- dbinom(x, n20, p1) b <- dbinom(x, n5, p5) d <- dbinom(x, n20, p5) par(mfcol=c(2,2)) barplot(a, names.arg=x, main="n=5, p=0.1") barplot(c, names.arg=x, main="n=20, p=0.1") barplot(b, names.arg=x, main="n=5, p=0.5") barplot(d, names.arg=x, main="n=20, p=0.5") par(mfcol=c(1,1))
When to approximate the binomial distribution with the normal
We saw in the last exercise that the binomial distribution looks very similar to the normal distribution where p is around 0.5, and n is around 20. As a general rule, you can use the normal distribution to approximate the binomial when np and nq are both greater than 5.
np 와 nq 모두가 5가 넘을 때
이 때 Normal distribution의 특징은 N(np, npq)


Before we use the normal distribution for the full 40 questions for Who Wants To Win A Swivel Chair, let’s tackle a simpler problem to make sure it works. Let’s try finding the probability that we get 5 or fewer questions correct out of 12, where there are only two possible choices for each question.
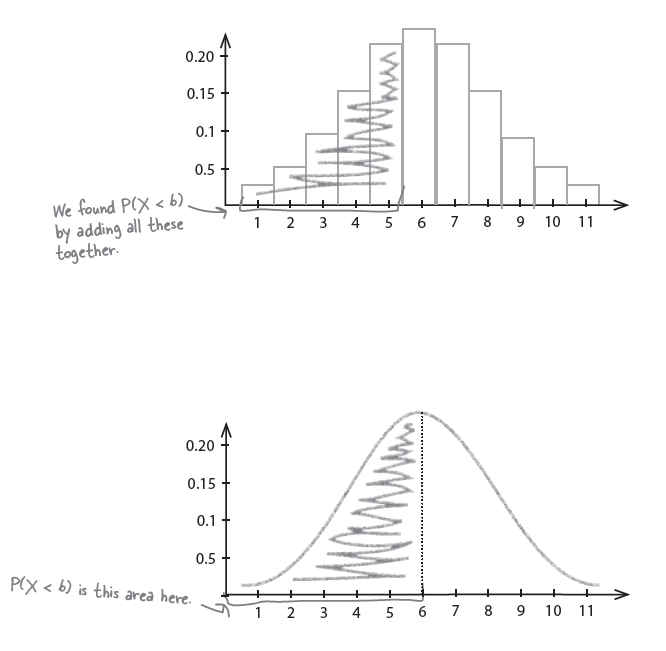
Let’s start off by working this out using the binomial distribution. Use the binomial distribution to find P(X < 6) where X ~ B(12, 0.5).
P(X < 6) 이므로, P(X=1), P(X=2), P(X=3), P(X=4), P(X=5) 까지 구하여 이를 더한다.
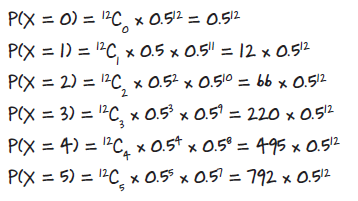

이를 R을 이용하여 구하면,
pbinom(5, 12, 1/2)
> pbinom(5, 12, 1/2) [1] 0.387207
위는 아래와 같음을 이해해야 한다
> sum(dbinom(c(0:5),12,1/2)) [1] 0.387207 >
교재의 조언에 따라서 Normal distribution으로 구하려면:
\begin{eqnarray*} X & \sim & B(12, 1/2) \\ n & = & 12 \\ p & = & 1/2 \\ q & = & 1/2 \end{eqnarray*}
이고, $np$와 $nq$ 모두가 5보다 크므로 Normal distribution에 대입하여 사용할 수 있다. 따라서 X 분포는 $X \sim N(np, nqp)$
를 따라야 한다. 즉, $X \sim N(6, 3)$일 때, P(X < 6)을 구해야 한다.
\begin{eqnarray*}
z & = & \frac {(6 - 6)}{\sqrt{3}} \\
& = & 0
\end{eqnarray*}
이에 대한 probability는 $P(X < 6) = 0.5$ 이다. 이 값은 앞에서 구한 binomial distribution 계산과 다른 값을 갖는다. 즉, $0.387 \ne 0.5$ 이다. 그 이유는 . . . .
Revisiting Normal Approximation
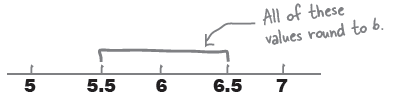
Apply a continuity correction
그렇다면, $X \sim N(6, 3)$의 조건에서 $P(X < 5.5) = ?$
\begin{eqnarray*}
z & = & \frac {(5.5-6)}{\sqrt{3}} \\
& = & - 0.29
\end{eqnarray*}
> pnorm(-0.29) [1] 0.3859081 # the below is the same as the above > n <- 12 > p <- 1/2 > q <- 1-p > pnorm(5.5, n*p, sqrt(n*p*q)) [1] 0.386415 >
이 값은 위의 0.387에 근사하다.
- In particular circumstances you can use the normal distribution to approximate the binomial. If X ~ B(n, p) and np > 5 and nq > 5 then you can approximate X using X ~ N(np, npq)
- If you’re approximating the binomial distribution with the normal distribution, then you need to apply a continuity correction to make sure your results are accurate.
Q:Does it really save time to approximate the binomial distribution with the normal?
A: It can save a lot of time. Calculating binomial probabilities can be time-consuming because you generally have to work out the probability of lots of different values. You have no way of simply calculating binomial probabilities over a range of values. If you approximate the binomial distribution with the normal distribution, then it’s a lot quicker. You can look probabilities up in standard tables and also deal with whole ranges at once.
Q:So is it really accurate?
A:Yes, It’s accurate enough for most purposes. The key thing to remember is that you need to apply a continuity correction. If you don’t then your results will be less accurate.
Q:What about continuity corrections for < and >? Do I treat those the same way as the ones for ≤ and ≥?
A: There’s a difference, and it all comes down to which values you want to include a nd exclude. When you’re working out probabilities using ≤ and ≥, you need to make sure that you include the value in the inequality in your probability range. So if, say, you need to work out P(X ≤ 10), you need to make sure your probability includes the value 10. This m eans you need to consider P(X < 10.5). When you’re working out probabilities using < or >, you need to make sure that you exclude the value in the inequality from your probability range. This means that if you need to work out P(X < 10), you need to make sure that your probability excludes 10. You need to consider P(X < 9.5).
Q:You can approximate the binomial distribution with both the normal and Poisson distributions. Which should I use?
A: It all depends on your circumstances. If X ~ B(n, p), then you can use the normal distribution to approximate the binomial d istribution if np > 5 and nq > 5. You can use the Poisson distribution to approximate the binomial distribution if n > 50 and p < 0.1
Remember, you need to apply a continuity correction when you approximate the binomial distribution with the normal distribution.
Pool Puzzle
X < 3 —- X < 2.5
X > 3 —- X > 3.5
X <_ 3 —- X < 3.5
X >_ 3 —- X > 2.5
3 <_ X < 10 —- 2.5 < X < 9.5
X = 0 —- -0.5 < X < 0.5
3 <_ X <_ 10 —- 2.5 < X < 10.5
3 < X <_ 10 —- 3.5 < X < 10.5
X > 0 —- X > 0.5
3 < X < 10 —- 3.5 < X < 9.5
exercise
What’s the probability of you winning the jackpot on today’s edition of Who Wants to Win a Swivel Chair? See if you can find the probability of getting at least 30 questions correct out of 40, where each question has a choice of 4 possible answers.
$X \sim B(40, 1/4)$ 분포에서 $P(X \ge 30)$를 구하는 문제.
$np = 40 * 1/4 = 10$
$npq = 40 * 1/4 * 3/4 = 10 * 3/4 = 7.5$
따라서 X ~ N(np, npq)라고 할 때, N(10, 7.5) . . . .
교재에는 왜 X ~ N(10, 30)이라고 하는지 모르겠음. . . .
\begin{eqnarray*} z & = & \frac {X - \mu}{\sigma} \\ & = & \frac {29.5 - 10}{\sqrt{7.5}} \\ & = & 7.120393 \end{eqnarray*}
z score = 7.120393 을 z-table에서 참조할 수는 없다. . . .
> pnorm(29.5, 10, sqrt(7.5)) [1] 1 > 1 - pnorm(29.5, 10, sqrt(7.5)) [1] 5.381251e-13 >
즉, 확율은 0에 가까움.
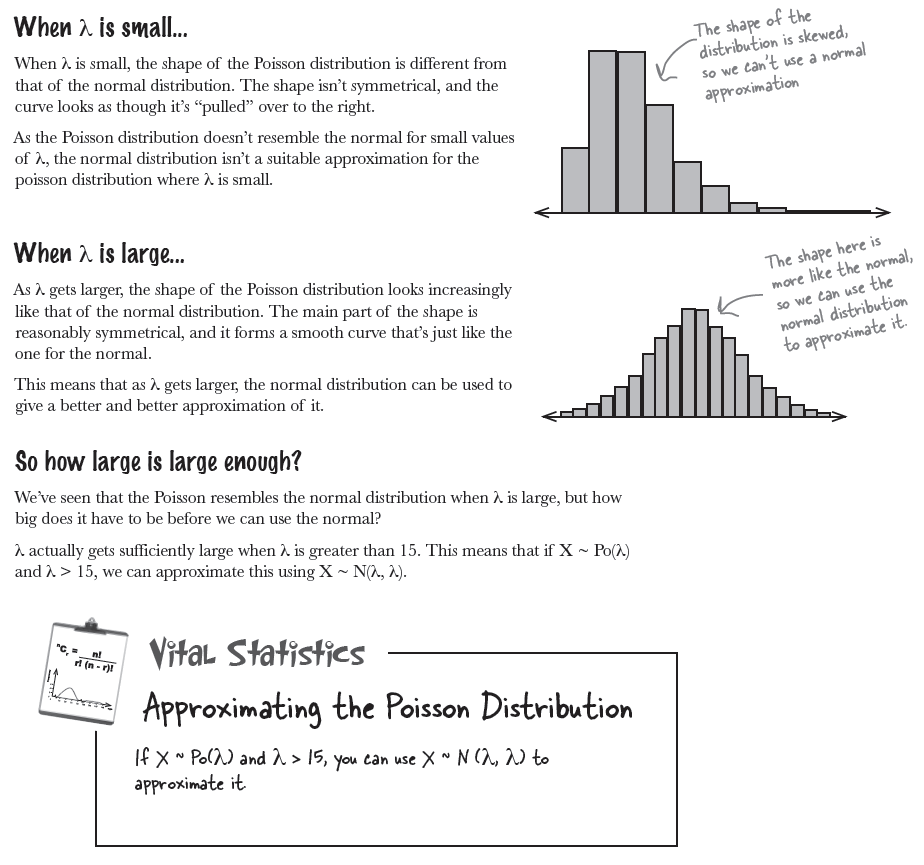
All aboard the Love Train
$\lambda > 15$ 일 때, Poisson distribution, $X \sim Po(\lambda)$는 $X \sim N(\lambda, \lambda)$ 의 성격을 취한다.
예)
par(mfcol=c(2,2)) barplot(dpois(c(1:10),.25), main = "lambda \n =0.25") barplot(dpois(c(1:20),5), main = "lambda \n = 5") barplot(dpois(c(1:10),1), main = "lambda \n = 1") barplot(dpois(c(1:40),20), main = "lambda \n = 20") par(mfcol=c(1,1))
Dexter’s found some statistics on the Internet about the model of roller coaster he’s been trying out, and according to one site, you can expect the ride to break down 40 times a year.
Given the huge profit the Love Train is bound to make, Dexter thinks that it’s still worth going ahead with the ride if there’s a high probability of it breaking down less than 52 times a year. So how do we work out that probability?
What sort of probability distribution does this follow? How would you work out the probability of the ride breaking down less than 52 times in a year?
$X \sim Po (\lambda = 40)$ 일 때 $P (X < 52)$ 를 구하는 문제
이 상황과 $N(\mu, \sigma^2)$ 상황을 같이 사용하는 것은 $X \sim N(\lambda, \lambda) $일 경우
$X \sim Po(40)$ 이므로
$X \sim N(40, 40)$ 일 때, $P(X < 52)$ 경우를 구하는 것
X < 52 일 때는 X < 51.5를 사용하고, $\mu = 40$, $\sigma = \sqrt{40}$을 사용한다.
\begin{eqnarray*}
z & = & \frac {51.5 - 40}{\sqrt{40}} \\
& = & 1.82
\end{eqnarray*}
> 11.5/sqrt(40) [1] 1.81831 > pnorm(1.82) [1] 0.9656205 # Or > pnorm(1.81831) [1] 0.9654916 # Or > pnorm(51.5, 40, sqrt(40)) [1] 0.9654916
$0.9654916 \sim 0.9656205$
Check up
| Situation | Distribution | Condition |
|---|---|---|
| $X + Y$ $\text{when}$ $X \sim N(\mu^{\;}_{X}, \sigma^{2}_{X})$ $Y\sim N(\mu^{ }_{Y}, \sigma^{2}_{Y}) \qquad\qquad $ | ||
| $X - Y$ $\text{when}$ $X \sim N(\mu^{\;}_{X}, \sigma^{2}_{X})$ $Y\sim N(\mu^{ }_{Y}, \sigma^{2}_{Y})$ | ||
| $aX + b$ $\text{when}$ $X \sim N(\mu_{X}, \sigma^{2}_{X})$ | $\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ | $\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$ |
| $X_{1} + X_{2} + . . . X_{n}$ $X \sim N(\mu, \sigma^{2})$ | $\qquad\qquad\qquad\qquad$ | $\qquad\qquad\qquad\qquad$ |
| $\text{Normal approximation of X} $ $X \sim B(n, p)$ | $\qquad\qquad\qquad\qquad$ | $\qquad\qquad\qquad\qquad$ |
| $\text{Normal approximation of X} $ $X \sim Po{\lambda}$ | $\qquad\qquad\qquad\qquad$ | $\qquad\qquad\qquad\qquad\;\;$ |
| Situation | Distribution | Condition |
|---|---|---|
| $X + Y$ $\text{when}$ $X \sim N(\mu^{\;}_{X}, \sigma^{2}_{X})$ $Y\sim N(\mu^{ }_{Y}, \sigma^{2}_{Y}) \qquad\qquad $ | $X + Y \sim N(\mu_{X} + \mu_{Y}, \sigma^{2}_{X} + \sigma^{2}_{Y}) \qquad\;\; $ | X, Y events are independent $\qquad$ |
| $X - Y$ $\text{when}$ $X \sim N(\mu^{\;}_{X}, \sigma^{2}_{X})$ $Y\sim N(\mu^{ }_{Y}, \sigma^{2}_{Y})$ | $X - Y \sim N(\mu_{X} - \mu_{Y}, \sigma^{2}_{X} + \sigma^{2}_{Y}) $ | X, Y events are independent |
| $aX + b$ $\text{when}$ $X \sim N(\mu_{X}, \sigma^{2}_{X})$ | $aX + b \sim N \left(a\mu_{X} + b, a^{2}\sigma^{2}_{X}\right)$ | a, b are constant. |
| $X_{1} + X_{2} + . . . X_{n}$ $X \sim N(\mu, \sigma^{2})$ | $X_{1} + X_{2} + . . . X_{n} \sim N(n\mu, n\sigma^2)$ | $X_{1} + X_{2} + . . . X_{n}$ are independent observation of X |
| $\text{Normal approximation of X} $ $X \sim B \left(n, p \right)$ | $X \sim N \left(np, npq\right)$ | $\text{when }\quad np > 5, \; nq > 5$ continuity correction required |
| $\text{Normal approximation of X} $ $X \sim Po \left(\lambda\right)$ | $X \sim N (\lambda, \lambda)$ | $\text{when }\quad \lambda > 15$ continuity correction required $\qquad\qquad\;\;\;$ |