r:regression
This is an old revision of the document!
Simple Regression in R
###########################
# regression sum up
###########################
rm(list = ls())
rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
set.seed(101)
n.s <- 36
m.x <- 100
df.x <- m.x - 1
ssq.x <- 100
x <- rnorm2(n.s, m.x, sqrt(9900/df.x))
y <- 5*x + rnorm2(n.s, 0, 36)
df <- data.frame(x,y)
mod.r <- lm(y ~ x, data = df)
summary(mod.r)
sp.xy <- sum((x-mean(x))*(y-mean(y)))
df.tot <- length(y) - 1
cov.xy <- sp.xy / df.tot
cov.xy
cov(x,y)
cor.xy <- cov.xy / ((sd(x)*sd(y)))
cor.xy
cor(x,y)
ss.x <- sum((x-mean(x))^2)
ss.x
b <- sp.xy / ss.x
b
a <- mean(y)- b*mean(x)
a
y.pred <- a + b*x
head(y.pred)
data.frame(head(mod.r$fitted.values))
mt <- paste("a = ", round(a,2),
"\n", "b = ", round(b,3))
plot(x,y, main=mt)
abline(h=mean(y), col="green", lwd=2)
# abline(v=mean(x), col="blue", lwd=2)
abline(mod.r, col="red", lwd=2)
x[35]
y[35]
y.obs.35 <- y[35]
y.hat.35 <- mod.r$fitted.values[35]
y.hat.35
y.mean <- mean(y)
points(x = x[35], y = y.obs.35, col = "blue", pch = 16)
points(x = x[35], y = y.hat.35, col = "red", pch = 16)
points(x = x[35], y = y.mean, col = "black", pch = 16)
abline(v=x[35])
text(x[35], y.obs.35, labels="y.obs", pos = 2)
text(x[35], y.hat.35, labels="y.hat", pos = 2)
text(x[35], y.mean, labels="y.mean", pos = 2)
y.hat <- mod.r$fitted.values
y.hat <- y.pred
y.obs <- y
y.mean <- y.mean
res <- y.obs - y.hat
reg <- y.hat - y.mean
df.a <- data.frame(y.obs, y.hat, y.mean, res, reg)
df.a
y.obs.35 - y.hat.35
y.hat.35 - y.mean
res.sq <- res^2
reg.sq <- reg^2
df.b <- data.frame(df.a, res.sq, reg.sq)
df.b
ss.res <- sum(res.sq)
ss.reg <- sum(reg.sq)
ss.tot <- sum((y.obs-y.mean)^2)
ss.res
ss.reg
ss.tot
ss.res + ss.reg
df.tot <- length(y)-1
df.res <- length(y)-ncol(df)
df.reg <- ncol(df)-1
df.tot
df.res
df.reg
df.res+df.reg
ms.tot <- ss.tot / df.tot
ms.reg <- ss.reg / df.reg
ms.res <- ss.res / df.res
ms.tot
ms.reg
ms.res
f.cal <- ms.reg/ms.res
f.cal
df.reg
df.res
pf(f.cal, df.reg, df.res, lower.tail = F)
summary(mod.r)
explained.area.in.y <- ss.reg / ss.tot
explained.area.in.y
r.sq <- explained.area.in.y
se.res <- sqrt(ss.res/(df.res)) # standard deviation of res
se.res
sqrt(ms.res)
ss.x <- sum((x-mean(x))^2) # ss for x
se.b.x <- sqrt(ms.res/ss.x) # se for b
se.b.x
b.x <- mod.r$coefficients[2]
b.x
t.cal <- b.x/se.b.x
t.cal
df.res
pv.t.cal <- pt(t.cal, df.res, lower.tail = F)*2
pv.t.cal
t.cal
df.res
mod.f <- aov(mod.r)
summary(mod.f)
##################################
# gradient descent
##################################
a <- rnorm(1)
b <- rnorm(1)
a.start <- a
b.start <- b
predict <- function(x, a, b){
return (a + b * x)
}
residuals <- function(predictions, y) {
return(y - predictions)
}
gradient <- function(x, y, predictions){
error = y - predictions
db = -2 * mean(x * error)
da = -2 * mean(error)
return(list("b" = db, "a" = da))
# return(c(db, da))
}
mseloss <- function(predictions, y) {
residuals <- (y - predictions)
return(mean(residuals^2))
}
# Train the model with scaled features
learning.rate = 1e-1
# Record Loss for each epoch:
# as = c()
# bs = c()
mses = c()
# sses = c()
# mres = c()
zx <- (x-mean(x))/sd(x)
nlen <- 75
for (epoch in 1:nlen) {
predictions <- predict(zx, a, b)
grad <- gradient(zx, y, predictions)
step.b <- grad$b * learning.rate
step.a <- grad$a * learning.rate
b <- b-step.b
a <- a-step.a
}
# mses
# mres
# as
# bs
# scaled
a
b
# unscale coefficients to make them comprehensible
# see http://commres.net/wiki/gradient_descent#why_normalize_scale_or_make_z-score_xi
# and
# http://commres.net/wiki/gradient_descent#how_to_unnormalize_unscale_a_and_b
#
a = a - (mean(x) / sd(x)) * b
b = b / sd(x)
a
b
cat(paste0("Intercept: ", a, "\n", "Slope: ", b, "\n"))
summary(lm(y~x))$coefficients
output
1
> ###########################
> # regression sum up
> ###########################
> rm(list = ls())
> rnorm2 <- function(n,mean,sd) {
> + mean+sd*scale(rnorm(n))
> + }
> set.seed(101)
> n.s <- 36
> m.x <- 100
> df.x <- m.x - 1
> ssq.x <- 100
> x <- rnorm2(n.s, m.x, sqrt(9900/df.x))
> y <- 5*x + rnorm2(n.s, 0, 36)
> df <- data.frame(x,y)
>
++++++++++++++++++++
2
> mod.r <- lm(y ~ x, data = df)
> summary(mod.r)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-91.412 -22.328 7.718 20.489 72.508
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -85.7661 60.2526 -1.423 0.164
x 5.8577 0.5996 9.769 2.12e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 35.47 on 34 degrees of freedom
Multiple R-squared: 0.7373, Adjusted R-squared: 0.7296
F-statistic: 95.43 on 1 and 34 DF, p-value: 2.115e-11
>
++++++++++++++++++++
3
> sp.xy <- sum((x-mean(x))*(y-mean(y)))
> df.tot <- length(y) - 1
> cov.xy <- sp.xy / df.tot
> cov.xy
[1] 585.7661
> cov(x,y)
[,1]
[1,] 585.7661
>
> cor.xy <- cov.xy / ((sd(x)*sd(y)))
> cor.xy
[1] 0.8586711
> cor(x,y)
[,1]
[1,] 0.8586711
>
++++++++++++++++++++
4
> ss.x <- sum((x-mean(x))^2) > ss.x [1] 3500 > b <- sp.xy / ss.x > b [1] 5.857661 > a <- mean(y)- b*mean(x) > a [1] -85.76606 > >
++++++++++++++++++++
5
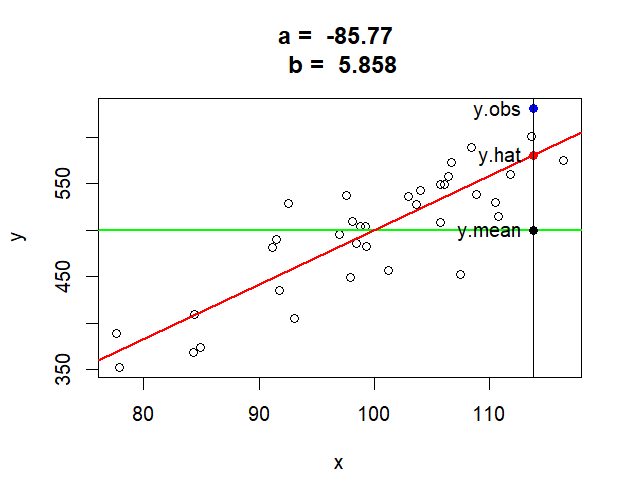
> y.pred <- a + b*x
> head(y.pred)
[,1]
[1,] 482.2777
[2,] 539.3226
[3,] 459.6216
[4,] 517.3681
[5,] 523.6284
[6,] 579.6797
>
> data.frame(head(mod.r$fitted.values))
head.mod.r.fitted.values.
1 482.2777
2 539.3226
3 459.6216
4 517.3681
5 523.6284
6 579.6797
>
> mt <- paste("a = ", round(a,2),
+ "\n", "b = ", round(b,3))
> plot(x,y, main=mt)
> abline(h=mean(y), col="green", lwd=2)
> # abline(v=mean(x), col="blue", lwd=2)
> abline(mod.r, col="red", lwd=2)
> x[35]
[1] 113.7788
> y[35]
[1] 630.7971
> y.obs.35 <- y[35]
> y.hat.35 <- mod.r$fitted.values[35]
> y.hat.35
35
580.7113
> y.mean <- mean(y)
>
> points(x = x[35], y = y.obs.35, col = "blue", pch = 16)
> points(x = x[35], y = y.hat.35, col = "red", pch = 16)
> points(x = x[35], y = y.mean, col = "black", pch = 16)
> abline(v=x[35])
> text(x[35], y.obs.35, labels="y.obs", pos = 2)
> text(x[35], y.hat.35, labels="y.hat", pos = 2)
> text(x[35], y.mean, labels="y.mean", pos = 2)
>
>
6
> y.hat <- mod.r$fitted.values
> y.hat <- y.pred
>
> y.obs <- y
> y.mean <- y.mean
>
> res <- y.obs - y.hat
> reg <- y.hat - y.mean
>
> df.a <- data.frame(y.obs, y.hat, y.mean, res, reg)
> df.a
y.obs y.hat y.mean res reg
1 495.2865 482.2777 500 13.0088479 -17.722299
2 572.8469 539.3226 500 33.5242925 39.322571
3 405.3625 459.6216 500 -54.2590625 -40.378431
4 536.0013 517.3681 500 18.6332683 17.368054
5 542.6492 523.6284 500 19.0208401 23.628375
6 601.0744 579.6797 500 21.3947218 79.679665
7 452.2171 543.6295 500 -91.4124153 43.629548
8 483.0325 496.1284 500 -13.0959080 -3.871624
9 515.3267 562.9955 500 -47.6688104 62.995518
10 509.9980 488.9515 500 21.0465311 -11.048516
11 557.9217 537.6334 500 20.2883651 37.633380
12 435.7639 451.8359 500 -16.0719728 -48.164119
13 574.9176 596.1593 500 -21.2417014 96.159349
14 368.6743 408.2015 500 -39.5272035 -91.798511
15 449.6582 488.0798 500 -38.4216090 -11.920198
16 485.6646 490.8944 500 -5.2298139 -9.105584
17 481.9870 448.2703 500 33.7166607 -51.729694
18 456.5535 507.2452 500 -50.6916186 7.245154
19 490.3326 450.3537 500 39.9789139 -49.646309
20 352.9357 370.3130 500 -17.3772823 -129.687034
21 504.1814 492.8153 500 11.3660873 -7.184671
22 589.5343 549.4563 500 40.0780792 49.456269
23 537.0947 486.0475 500 51.0471491 -13.952464
24 409.3543 408.3897 500 0.9646127 -91.610336
25 538.2055 551.7883 500 -13.5828576 51.788309
26 374.5917 411.8657 500 -37.2740105 -88.134288
27 508.1914 533.7775 500 -25.5860867 33.777536
28 504.6137 495.7007 500 8.9129424 -4.299270
29 549.0252 533.7887 500 15.2365812 33.788663
30 549.3653 535.7949 500 13.5703706 35.794919
31 530.1250 561.5610 500 -31.4359983 61.561044
32 528.0982 521.5753 500 6.5228603 21.575326
33 560.5632 568.8940 500 -8.3308199 68.894006
34 389.1352 368.8325 500 20.3026105 -131.167455
35 630.7971 580.7113 500 50.0858331 80.711286
36 528.9194 456.4118 500 72.5076032 -43.588169
>
> y.obs.35 - y.hat.35
35
50.08583
> y.hat.35 - y.mean
35
80.71129
>
> res.sq <- res^2
> reg.sq <- reg^2
> df.b <- data.frame(df.a, res.sq, reg.sq)
> df.b
y.obs y.hat y.mean res reg res.sq
1 495.2865 482.2777 500 13.0088479 -17.722299 169.2301237
2 572.8469 539.3226 500 33.5242925 39.322571 1123.8781868
3 405.3625 459.6216 500 -54.2590625 -40.378431 2944.0458598
4 536.0013 517.3681 500 18.6332683 17.368054 347.1986863
5 542.6492 523.6284 500 19.0208401 23.628375 361.7923589
6 601.0744 579.6797 500 21.3947218 79.679665 457.7341189
7 452.2171 543.6295 500 -91.4124153 43.629548 8356.2296621
8 483.0325 496.1284 500 -13.0959080 -3.871624 171.5028055
9 515.3267 562.9955 500 -47.6688104 62.995518 2272.3154845
10 509.9980 488.9515 500 21.0465311 -11.048516 442.9564724
11 557.9217 537.6334 500 20.2883651 37.633380 411.6177585
12 435.7639 451.8359 500 -16.0719728 -48.164119 258.3083084
13 574.9176 596.1593 500 -21.2417014 96.159349 451.2098789
14 368.6743 408.2015 500 -39.5272035 -91.798511 1562.3998194
15 449.6582 488.0798 500 -38.4216090 -11.920198 1476.2200395
16 485.6646 490.8944 500 -5.2298139 -9.105584 27.3509539
17 481.9870 448.2703 500 33.7166607 -51.729694 1136.8132091
18 456.5535 507.2452 500 -50.6916186 7.245154 2569.6401982
19 490.3326 450.3537 500 39.9789139 -49.646309 1598.3135561
20 352.9357 370.3130 500 -17.3772823 -129.687034 301.9699398
21 504.1814 492.8153 500 11.3660873 -7.184671 129.1879413
22 589.5343 549.4563 500 40.0780792 49.456269 1606.2524356
23 537.0947 486.0475 500 51.0471491 -13.952464 2605.8114284
24 409.3543 408.3897 500 0.9646127 -91.610336 0.9304776
25 538.2055 551.7883 500 -13.5828576 51.788309 184.4940217
26 374.5917 411.8657 500 -37.2740105 -88.134288 1389.3518589
27 508.1914 533.7775 500 -25.5860867 33.777536 654.6478348
28 504.6137 495.7007 500 8.9129424 -4.299270 79.4405414
29 549.0252 533.7887 500 15.2365812 33.788663 232.1534061
30 549.3653 535.7949 500 13.5703706 35.794919 184.1549582
31 530.1250 561.5610 500 -31.4359983 61.561044 988.2219908
32 528.0982 521.5753 500 6.5228603 21.575326 42.5477061
33 560.5632 568.8940 500 -8.3308199 68.894006 69.4025607
34 389.1352 368.8325 500 20.3026105 -131.167455 412.1959914
35 630.7971 580.7113 500 50.0858331 80.711286 2508.5906729
36 528.9194 456.4118 500 72.5076032 -43.588169 5257.3525227
reg.sq
1 314.07989
2 1546.26461
3 1630.41773
4 301.64929
5 558.30011
6 6348.84894
7 1903.53748
8 14.98947
9 3968.43534
10 122.06970
11 1416.27132
12 2319.78237
13 9246.62035
14 8426.96671
15 142.09111
16 82.91166
17 2675.96119
18 52.49225
19 2464.75603
20 16818.72676
21 51.61950
22 2445.92253
23 194.67126
24 8392.45357
25 2682.02895
26 7767.65273
27 1140.92197
28 18.48372
29 1141.67377
30 1281.27626
31 3789.76215
32 465.49470
33 4746.38400
34 17204.90124
35 6514.31162
36 1899.92850
> ss.res <- sum(res.sq)
> ss.reg <- sum(reg.sq)
> ss.tot <- sum((y.obs-y.mean)^2)
> ss.res
[1] 42785.46
> ss.reg
[1] 120092.7
> ss.tot
[1] 162878.1
> ss.res + ss.reg
[1] 162878.1
>
> df.tot <- length(y)-1
> df.res <- length(y)-ncol(df)
> df.reg <- ncol(df)-1
> df.tot
[1] 35
> df.res
[1] 34
> df.reg
[1] 1
> df.res+df.reg
[1] 35
>
>
++++++++++++++++++++
7
> ms.tot <- ss.tot / df.tot > ms.reg <- ss.reg / df.reg > ms.res <- ss.res / df.res > ms.tot [1] 4653.661 > ms.reg [1] 120092.7 > ms.res [1] 1258.396 >
++++++++++++++++++++
8
> f.cal <- ms.reg/ms.res
> f.cal
[1] 95.43312
> df.reg
[1] 1
> df.res
[1] 34
> pf(f.cal, df.reg, df.res, lower.tail = F)
[1] 2.115182e-11
> summary(mod.r)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-91.412 -22.328 7.718 20.489 72.508
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -85.7661 60.2526 -1.423 0.164
x 5.8577 0.5996 9.769 2.12e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 35.47 on 34 degrees of freedom
Multiple R-squared: 0.7373, Adjusted R-squared: 0.7296
F-statistic: 95.43 on 1 and 34 DF, p-value: 2.115e-11
>
> explained.area.in.y <- ss.reg / ss.tot
> explained.area.in.y
[1] 0.7373161
> r.sq <- explained.area.in.y
>
++++++++++++++++++++
9
> se.res <- sqrt(ss.res/(df.res)) # standard deviation of res > se.res [1] 35.47388 > sqrt(ms.res) [1] 35.47388 >
++++++++++++++++++++
10
> ss.x <- sum((x-mean(x))^2) # ss for x
> se.b.x <- sqrt(ms.res/ss.x) # se for b
> se.b.x
[1] 0.599618
> b.x <- mod.r$coefficients[2]
> b.x
x
5.857661
> t.cal <- b.x/se.b.x
> t.cal
x
9.768988
> df.res
[1] 34
> pv.t.cal <- pt(t.cal, df.res, lower.tail = F)*2
> pv.t.cal
x
2.115182e-11
> t.cal
x
9.768988
> df.res
[1] 34
> t.cal^2
x
95.43312
>
> mod.f <- aov(mod.r)
> summary(mod.f)
Df Sum Sq Mean Sq F value Pr(>F)
x 1 120093 120093 95.43 2.12e-11 ***
Residuals 34 42785 1258
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
++++++++++++++++++++
11
> ##################################
> # gradient descent
> ##################################
> predict <- function(x, a, b){
+ return (a + b * x)
+ }
>
> residuals <- function(predictions, y) {
+ return(y - predictions)
+ }
>
> gradient <- function(x, y, predictions){
+ error = y - predictions
+ db = -2 * mean(x * error)
+ da = -2 * mean(error)
+ return(list("b" = db, "a" = da))
+ }
>
> mseloss <- function(predictions, y) {
+ residuals <- (y - predictions)
+ return(mean(residuals^2))
+ }
>
++++++++++++++++++++
12
> # Train the model with scaled features > learning.rate = 1e-1 >
++++++++++++++++++++
13
> a <- rnorm(1) > b <- rnorm(1) > a.init <- a > b.init <- b > > zx <- (x-mean(x))/sd(x) >
++++++++++++++++++++
14
> nlen <- 75
> for (epoch in 1:nlen) {
+ predictions <- predict(zx, a, b)
+
+ grad <- gradient(zx, y, predictions)
+
+ step.b <- grad$b * learning.rate
+ step.a <- grad$a * learning.rate
+ b <- b-step.b
+ a <- a-step.a
+ }
>
> # scaled a and b
> a
[1] 500
> b
[1] 58.5766
>
> # unscale coefficients to make them comprehensible
> # see http://commres.net/wiki/gradient_descent#why_normalize_scale_or_make_z-score_xi
> # and
> # http://commres.net/wiki/gradient_descent#how_to_unnormalize_unscale_a_and_b
> #
> a = a - (mean(x) / sd(x)) * b
> b = b / sd(x)
> a
[1] -85.76604
> b
[1] 5.85766
>
> cat(paste0("Intercept: ", a, "\n", "Slope: ", b, "\n"))
Intercept: -85.7660381466164
Slope: 5.85766011248848
> summary(lm(y~x))$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) -85.766064 60.252573 -1.423442 1.637203e-01
x 5.857661 0.599618 9.768988 2.115182e-11
>
++++++++++++++++++++
r/regression.1760308739.txt.gz · Last modified: by hkimscil