r:sampling_distribution
This is an old revision of the document!
Table of Contents
PS1. week02
rm(list=ls())
rnorm2 <- function(n,mean,sd){
mean+sd*scale(rnorm(n))
}
se <- function(sample) {
sd(sample)/sqrt(length(sample))
}
ss <- function(x) {
sum((x-mean(x))^2)
}
################################
N.p <- 1000000
m.p <- 100
sd.p <- 10
p1 <- rnorm2(N.p, m.p, sd.p)
mean(p1)
sd(p1)
p2 <- rnorm2(N.p, m.p+20, sd.p)
mean(p2)
sd(p2)
m.p1 <- mean(p1)
sd.p1 <- sd(p1)
var(p1)
hist(p1, breaks=100, col=rgb(1,1,1,1))
abline(v=mean(p1),lwd=2)
abline(v=mean(p1)-sd(p1), lwd=2)
abline(v=mean(p1)+sd(p1), lwd=2)
abline(v=c(m.p1-2*sd.p1, m.p1+2*sd.p1), lwd=2, col='red')
abline(v=c(m.p1-3*sd.p1, m.p1+3*sd.p1), lwd=2, col='green')
# area bet black = 68%
# between red = 95%
# between green = 99%
pnorm(m.p1+sd.p1, m.p1, sd.p1)
pnorm(m.p1-sd.p1, m.p1, sd.p1)
pnorm(m.p1+sd.p1, m.p1, sd.p1) -
pnorm(m.p1-sd.p1, m.p1, sd.p1)
pnorm(m.p1+2*sd.p1, m.p1, sd.p1) -
pnorm(m.p1-2*sd.p1, m.p1, sd.p1)
pnorm(m.p1+3*sd.p1, m.p1, sd.p1) -
pnorm(m.p1-3*sd.p1, m.p1, sd.p1)
m.p1
sd.p1
(m.p1-m.p1)/sd.p1
((m.p1-sd.p1) - m.p1) / sd.p1
(120-100)/10
pnorm(1)-pnorm(-1)
pnorm(2)-pnorm(-2)
pnorm(3)-pnorm(3)
1-pnorm(-2)*2
pnorm(2)-pnorm(-2)
pnorm(120, 100, 10)
pnorm(2)-pnorm(-2)
zscore <- (120-100)/10
pnorm(zscore)-pnorm(-zscore)
zscore
# reminder.
pnorm(-1)
pnorm(1, 0, 1, lower.tail = F)
pnorm(110, 100, 10, lower.tail = F)
zscore <- (110-100)/10
pnorm(zscore, lower.tail = F)
pnorm(118, 100, 10, lower.tail = F)
pnorm(18/10, lower.tail = F)
z.p1 <- (p1-mean(p1))/sd(p1)
mean(z.p1)
round(mean(z.p1),10)
sd(z.p1)
pnorm(1.8)-pnorm(-1.8)
hist(z.p1, breaks=100, col=rgb(0,0,0,0))
abline(v=c(m.p1, -1.8, 1.8), col='red')
1-(pnorm(1.8)-pnorm(-1.8))
pnorm(1)-pnorm(-1)
1-(pnorm(-1)*2)
pnorm(2)-pnorm(-2)
1-(pnorm(-2)*2)
1-(pnorm(-3)*2)
#
hist(p1, breaks=100, col=rgb(1,1,1,1))
abline(v=mean(p1),lwd=2)
abline(v=mean(p1)-sd(p1), lwd=2)
abline(v=mean(p1)+sd(p1), lwd=2)
abline(v=c(m.p1-2*sd.p1, m.p1+2*sd.p1), lwd=2, col='red')
abline(v=c(m.p1-3*sd.p1, m.p1+3*sd.p1), lwd=2, col='green')
# 68%
a <- qnorm(.32/2)
b <- qnorm(1-.32/2)
c(a, b)
c(-1, 1)
# 95%
c <- qnorm(.05/2)
d <- qnorm(1-.05/2)
c(c, d)
c(-2,2)
# 99%
e <- qnorm(.01/2)
f <- qnorm(1-.01/2)
c(e,f)
c(-3,3)
pnorm(b)-pnorm(a)
c(a, b)
pnorm(d)-pnorm(c)
c(c, d)
pnorm(f)-pnorm(e)
c(e, f)
qnorm(.5)
qnorm(1)
################################
hist(p1, breaks=50, col = rgb(1, 0, 0, 0.5),
main = "histogram of p1 and p2",)
abline(v=mean(p1), col="black", lwd=3)
hist(p2, add=T, breaks=50, col=rgb(0,0,1,.5))
abline(v=mean(p2), col="violet", lwd=3)
s.size <- 10
means.temp <- c()
s1 <- sample(p1, s.size, replace = T)
mean(s1)
means.temp <- append(means.temp, mean(s1))
means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T)))
means.temp
iter <- 1000000
# means <- c()
means <- rep(NA, iter)
for (i in 1:iter) {
# means <- append(means, mean(sample(p1, s.size, replace = T)))
means[i] <- mean(sample(p1, s.size, replace = T))
}
length(means)
mean(means)
sd(means)
se.s <- sd(means)
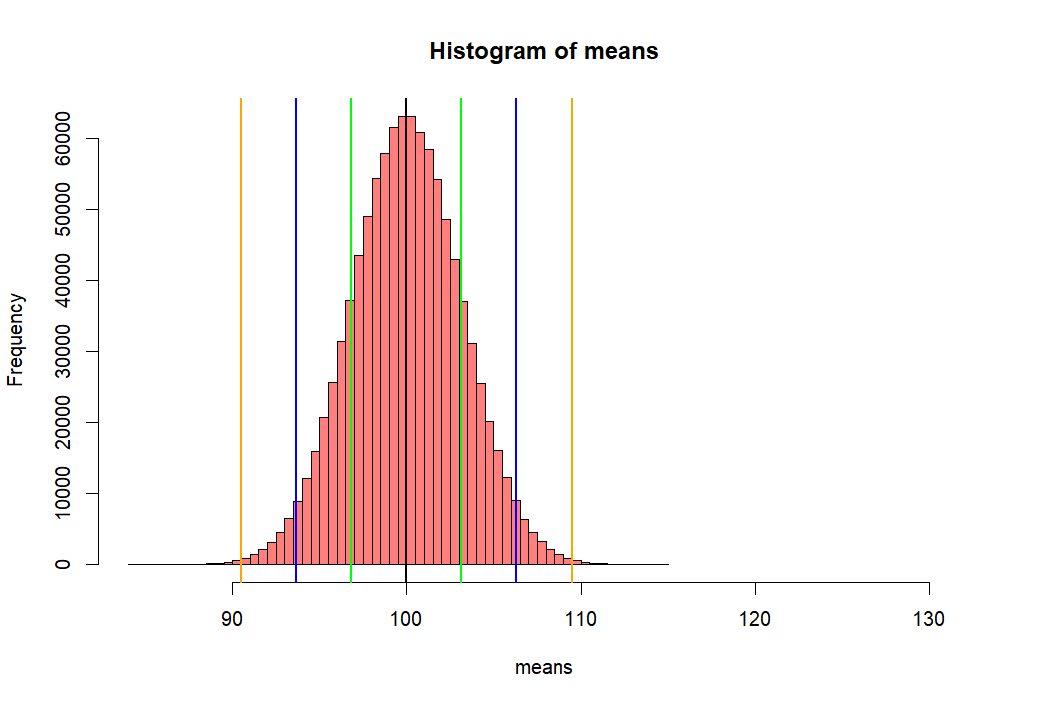
hist(means, breaks=100, col=rgb(.1, 0, 0, .5))
abline(v=mean(means), col="red", lwd=2)
# now we want to get sd of this distribution
lo1 <- mean(means)-se.s
hi1 <- mean(means)+se.s
lo2 <- mean(means)-2*se.s
hi2 <- mean(means)+2*se.s
lo3 <- mean(means)-3*se.s
hi3 <- mean(means)+3*se.s
hist(means,
xlim = c(mean(means)-5*sd(means), mean(means)+10*sd(means)),
col = rgb(1, 0, 0, .5))
abline(v=mean(means), col="black", lwd=2)
# abline(v=mean(p2), colo='darkgreen', lwd=3)
abline(v=c(lo1, hi1, lo2, hi2, lo3, hi3),
col=c("green","green", "blue", "blue", "orange", "orange"),
lwd=2)
# meanwhile . . . .
se.s
se.z <- sqrt(var(p1)/s.size)
se.z <- c(se.z)
se.z
# sd of sample means (sd(means))
# is sqrt(var(s1)/s.size) or
# sd(s1) / sqrt(s.size)
# = se.s
# when iter value goes to
# unlimited value:
# mean(means) = mean(p1)
# and
# sd(means) = sd(p1) / sqrt(s.size)
# that is, sd(means) = se.z
# This is called CLT (Central Limit Theorem)
mean(means)
mean(p1)
sd(means)
var(p1)
sqrt(var(p1)/s.size)
se.z
sd(means)
se.s
se.z
# because CLT
loz1 <- mean(p1)-se.z
hiz1 <- mean(p1)+se.z
loz2 <- mean(p1)-2*se.z
hiz2 <- mean(p1)+2*se.z
loz3 <- mean(p1)-3*se.z
hiz3 <- mean(p1)+3*se.z
c(lo1, loz1)
c(lo2, loz2)
c(lo3, loz3)
c(hi1, hiz1)
c(hi2, hiz2)
c(hi3, hiz3)
hist(means,
xlim = c(mean(means)-5*sd(means), mean(means)+10*sd(means)),
col = rgb(1, 0, 0, .5))
abline(v=mean(means), col="black", lwd=2)
# abline(v=mean(p2), colo='darkgreen', lwd=3)
abline(v=c(lo1, hi1, lo2, hi2, lo3, hi3),
col=c("green","green", "blue", "blue", "orange", "orange"),
lwd=2)
round(c(lo1, hi1))
round(c(lo2, hi2))
round(c(lo3, hi3))
round(c(loz1, hiz1))
round(c(loz2, hiz2))
round(c(loz3, hiz3))
m.sample.i.got <- mean(means)+ 1.5*sd(means)
m.sample.i.got
hist(means,
xlim = c(mean(means)-10*sd(means), mean(means)+10*sd(means)),
col = rgb(1, 0, 0, .5))
abline(v=mean(means), col="black", lwd=3)
abline(v=m.sample.i.got, col='darkgreen', lwd=3)
# what is the probablity of getting
# greater than
# m.sample.i.got?
m.sample.i.got
pnorm(m.sample.i.got, mean(means), sd(means), lower.tail = F)
pnorm(m.sample.i.got, mean(p1), se.z, lower.tail = F)
# then, what is the probabilty of getting
# greater than m.sample.i.got and
# less than corresponding value, which is
# mean(means) - m.sample.i.got - mean(means)
# (green line)
tmp <- mean(means) - (m.sample.i.got - mean(means))
abline(v=tmp, col='green', lwd=3)
2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F)
m.sample.i.got
### one more time
mean(p2)
sd(p2)
sample(p2, s.size)
m.sample.i.got <- mean(sample(p2, s.size))
m.sample.i.got
hist(means,
xlim = c(mean(means)-15*sd(means), mean(means)+15*sd(means)),
col = rgb(1, 0, 0, .5))
abline(v=mean(means), col="black", lwd=2)
abline(v=m.sample.i.got, col='darkgreen', lwd=2)
# what is the probablity of getting
# greater than
# m.sample.i.got?
m.sample.i.got
pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F)
# then, what is the probabilty of getting
# greater than m.sample.i.got and
# less than corresponding value, which is
# mean(means) - m.sample.i.got - mean(means)
# (green line)
tmp <- mean(means) - (m.sample.i.got - mean(means))
abline(v=tmp, col='green', lwd=2)
2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F)
output
> rm(list=ls())
> rnorm2 <- function(n,mean,sd){
+ mean+sd*scale(rnorm(n))
+ }
>
> ss <- function(x) {
+ sum((x-mean(x))^2)
+ }
>
….
필요한 펑션
- rnorm2는 평균과 표준편차값을 (mean, sd) 갖는 n 개의 샘플을 랜덤하게 추출하는 것
- ss는 sum of square 값을 구하는 펑션
- ss는 ss/n-1 의 variance 혹은 mean square값을 구할 때의 분자부분으로
- error 혹은 residual의 제곱의 합이라고 부를 수 있다 (variance 참조)
> ################################
> N.p <- 1000000
> m.p <- 100
> sd.p <- 10
>
> p1 <- rnorm2(N.p, m.p, sd.p)
> mean(p1)
[1] 100
> sd(p1)
[1] 10
>
> p2 <- rnorm2(N.p, m.p+20, sd.p)
> mean(p2)
[1] 120
> sd(p2)
[1] 10
>
> m.p1 <- mean(p1)
> sd.p1 <- sd(p1)
> var(p1)
[,1]
[1,] 100
>
- rnorm2 펑션을 이용하여 p1과 p2 모집단을 구한다.
- 각 모집단의 평균은 100과 120이고, 표준편차는 모두 10이다.
- 모집단의 크기는 각각 백만이다.
pnorm
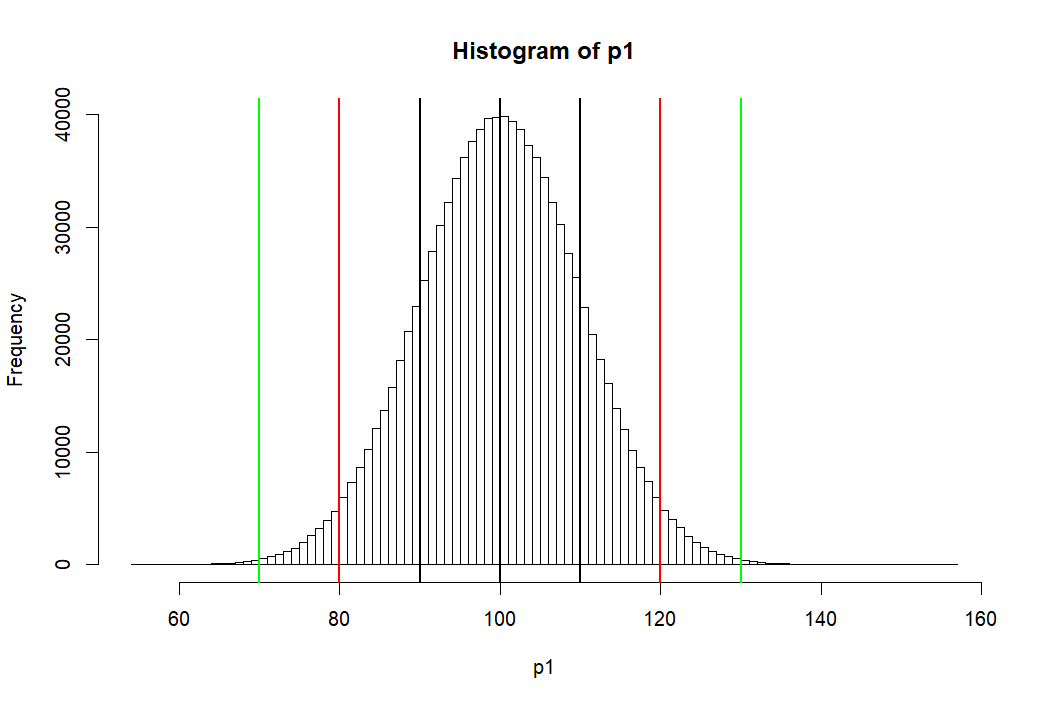
모집단 P1의 히스토그램 (histgram of P1)
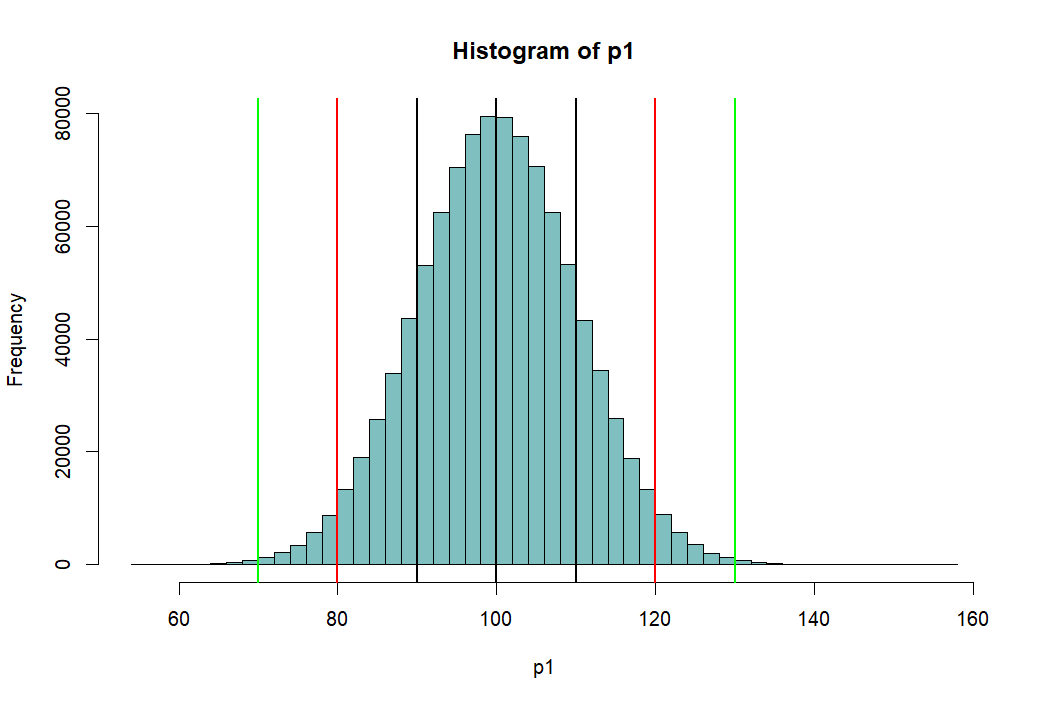
> hist(p1, breaks=100, col=rgb(1,1,1,1)) > abline(v=mean(p1),lwd=2) > abline(v=mean(p1)-sd(p1), lwd=2) > abline(v=mean(p1)+sd(p1), lwd=2) > abline(v=c(m.p1-2*sd.p1, m.p1+2*sd.p1), lwd=2, col='red') > abline(v=c(m.p1-3*sd.p1, m.p1+3*sd.p1), lwd=2, col='green') > > # area bet black = 68% > # between red = 95% > # between green = 99% > > pnorm(m.p1+sd.p1, m.p1, sd.p1) [1] 0.8413447 > pnorm(m.p1-sd.p1, m.p1, sd.p1) [1] 0.1586553 > pnorm(m.p1+sd.p1, m.p1, sd.p1) - + pnorm(m.p1-sd.p1, m.p1, sd.p1) [1] 0.6826895 > > pnorm(m.p1+2*sd.p1, m.p1, sd.p1) - + pnorm(m.p1-2*sd.p1, m.p1, sd.p1) [1] 0.9544997 > > pnorm(m.p1+3*sd.p1, m.p1, sd.p1) - + pnorm(m.p1-3*sd.p1, m.p1, sd.p1) [1] 0.9973002 > > m.p1 [1] 100 > sd.p1 [1] 10 > > (m.p1-m.p1)/sd.p1 [1] 0 > ((m.p1-sd.p1) - m.p1) / sd.p1 [1] -1 > (120-100)/10 [1] 2 > pnorm(1)-pnorm(-1) [1] 0.6826895 > pnorm(2)-pnorm(-2) [1] 0.9544997 > pnorm(3)-pnorm(-3) [1] 0.9973002 > > 1-pnorm(-2)*2 [1] 0.9544997 > pnorm(2)-pnorm(-2) [1] 0.9544997 > > pnorm(120, 100, 10) [1] 0.9772499 > pnorm(2)-pnorm(-2) [1] 0.9544997 > > > > > > > >
….
pnorm 펑션
- 위의 histogram에서 검정색의 선은 p1의 standard deviation값인 10씩 좌우로 그린것 (90과 110)
- 붉은 색선은 80, 120
- 녹색선은 70, 130 선을 말한다
- 고등학교 때, Normal distribution (정상분포의) 경우
- 평균을 중심으로 위아래로 SD값 하나씩 간 간격의 probability는 (면적은) 68%
- 두 개씩 간 값은 95%
- 세 개씩 간 값은 99% 라고 배웠다.
- pnorm은 percentage를 구하는 R의 명령어
- pnorm(m.p1+sd.p1, m.p1, sd.p1) 은
- 정규분포곡선에서
- 평균값과 표준편차값을 더한 값 (100+10=110) 을 기준으로
- 왼쪽의 부분이 몇 퍼센트인가를 구해주는 명령어
- m.p1+sd.p1은 110이므로
- 오른 쪽 검정색을 기준으로 왼쪽의 퍼센티지를 묻는 것
- 답은 0.8413447
- pnorm(m.p1-sd.p1, m.p1, sd.p1) - pnorm(90, 100, 10)이므로
- 왼쪽 검정색 선을 기준으로 왼쪽의 퍼센티지를 묻는 것
- 답은 0.1586553
- 전자에서 후자를 빼 준 값은 두개의 검정색 선의 안쪽 면적으로 묻는 것
- 답은 0.6826895
- 이 0.6826895 이 우리가 배운 68%
- 그렇다면 두 개씩 간 면적은 (붉은 색 선의 안쪽 부분)
- pnorm(m.p1+2*sd.p1, m.p1, sd.p1) - pnorm(m.p1-2*sd.p1, m.p1, sd.p1) = 0.9544997
- 0.9544997 혹은 95.44997%
- 이것이 우리가 배운 95%
- 마찬가지로 녹색선 가운데 부분은 pnorm(m.p1+3*sd.p1, m.p1, sd.p1) - pnorm(m.p1-3*sd.p1, m.p1, sd.p1) 로 구할 수 있는데 답은
- 0.9973002
- pnorm명령어는 pnorm(score, mean, sd)와 같이 사용하여 퍼센티지값을 구할 수 있는데
- pnorm(score)만으로 구하면, mean과 sd가 각각 0, 1을 default값으로 하고 생략이 된 것
- 위의 p1 모집단도 두번째 방법으로 구해 볼 수 있는데, 그렇게 하기 위해서
- p1을 표준점수화 하면 됨
- 표준점수화 한다는 뜻은 p1집합의 평균과 표준편차 값을 0과 1로 만든다는 것
- p1 모든 원소를 표준점수화하는 것은 각 점수와 평균점수 간의 차이에 sd가 몇개나 들어가는 지 구하는 것. 즉,
- $ \dfrac {(\text{score} - \text{m.p1})} {\text{sd.p1}} $
- 100점은 표준점수로 0이 된다 $ (100-100) / 10 = 0 $
- 110점은 1
- 90점은 -1
- 115점은 1.5
- 130점은 30/10 = 3 점으로 계산될 수 있다.
- 그렇다면 위의 pnorm(m.p1+sd.p1, m.p1, sd.p1)은 pnorm(1)과 같은 것
- pnorm(110, 100, 10) 이고 이 때 110점은 표준점수로 1 이다.
- 따라서 위의 68%, 95%, 99%는 pnorm(1)-pnorm(-1)과 같이 구할 수 있다.
z score, 표준점수
> zscore <- (120-100)/10 > pnorm(zscore)-pnorm(-zscore) [1] 0.9544997 > zscore [1] 2 > > > pnorm(-1) [1] 0.1586553 > pnorm(1, 0, 1, lower.tail = F) [1] 0.1586553 > pnorm(110, 100, 10, lower.tail = F) [1] 0.1586553 > zscore <- (110-100)/10 > pnorm(zscore, lower.tail = F) [1] 0.1586553 > > pnorm(118, 100, 10, lower.tail = F) [1] 0.03593032 > pnorm(18/10, lower.tail = F) [1] 0.03593032 >
….
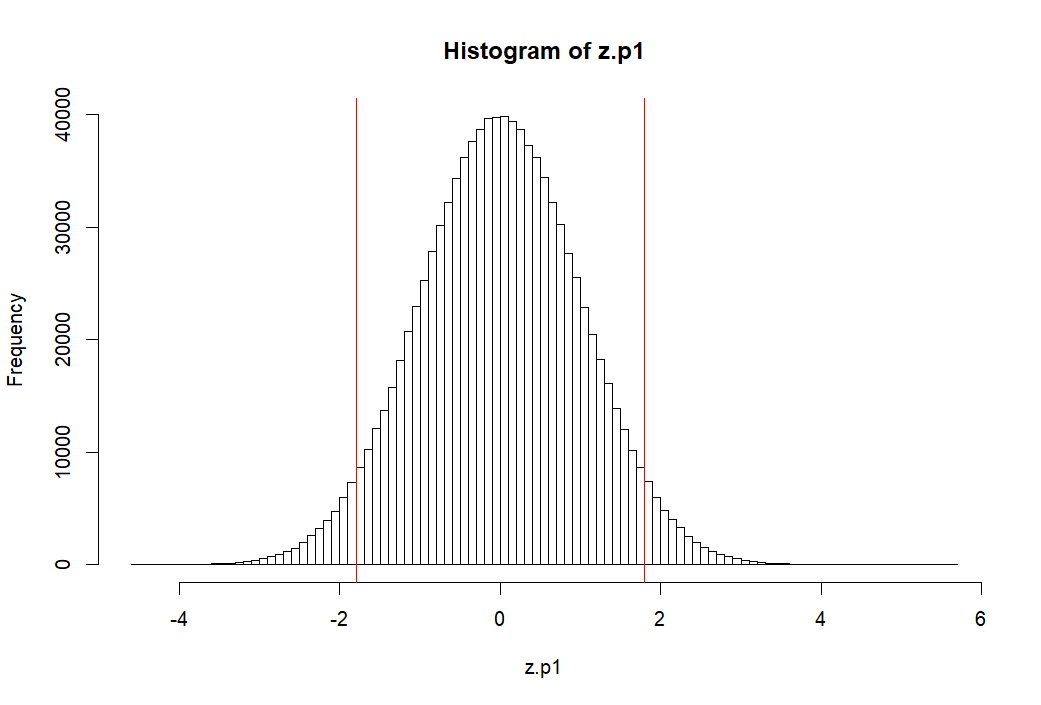
> z.p1 <- (p1-mean(p1))/sd(p1) > mean(z.p1) [1] -2.319195e-17 > round(mean(z.p1),10) [1] 0 > sd(z.p1) [1] 1 > pnorm(1.8)-pnorm(-1.8) [1] 0.9281394 > > hist(z.p1, breaks=100, col=rgb(0,0,0,0)) > abline(v=c(m.p1, -1.8, 1.8), col='red') > 1-(pnorm(1.8)-pnorm(-1.8)) [1] 0.07186064 > >
….
p1 모집단의 모든 원소를 표준점수화 하기
- z.p1 ← (p1-mean(p1))/sd(p1)
- 평균과 표준편차는 각각 0, 1이 된다 (mean(z.p1), sd(z.p1))
- 그렇다면 이 표준점수화한 분포에서 -1.8과 1.8 사이를 제외한 바깥 쪽 부분의 면적은 (probability는)
- 1-(p(1.8)-p(-1.8))과 같이 구할 수 있다.
- 답은 약 7% 정도
> pnorm(1)-pnorm(-1) [1] 0.6826895 > 1-(pnorm(-1)*2) [1] 0.6826895 > > pnorm(2)-pnorm(-2) [1] 0.9544997 > 1-(pnorm(-2)*2) [1] 0.9544997 > > 1-(pnorm(-3)*2) [1] 0.9973002 >
….
qnorm
> # > hist(p1, breaks=100, col=rgb(1,1,1,1)) > abline(v=mean(p1),lwd=2) > abline(v=mean(p1)-sd(p1), lwd=2) > abline(v=mean(p1)+sd(p1), lwd=2) > abline(v=c(m.p1-2*sd.p1, m.p1+2*sd.p1), lwd=2, col='red') > abline(v=c(m.p1-3*sd.p1, m.p1+3*sd.p1), lwd=2, col='green') > > # 68% > a <- qnorm(.32/2) > b <- qnorm(1-.32/2) > c(a, b) [1] -0.9944579 0.9944579 > c(-1, 1) [1] -1 1 > > # 95% > c <- qnorm(.05/2) > d <- qnorm(1-.05/2) > c(c, d) [1] -1.959964 1.959964 > c(-2,2) [1] -2 2 > # 99% > e <- qnorm(.01/2) > f <- qnorm(1-.01/2) > c(e,f) [1] -2.575829 2.575829 > c(-3,3) [1] -3 3 > > pnorm(b)-pnorm(a) [1] 0.68 > c(a, b) [1] -0.9944579 0.9944579 > pnorm(d)-pnorm(c) [1] 0.95 > c(c, d) [1] -1.959964 1.959964 > pnorm(f)-pnorm(e) [1] 0.99 > c(e, f) [1] -2.575829 2.575829 > > qnorm(.5) [1] 0 > qnorm(1) [1] Inf > >
….
- qnorm는 pnorm의 반대값을 구하는 명령어
- 히스토그램에서 검정 색 부분의 바깥 쪽 부분은 32%이고 왼 쪽의 것은 이것의 반인 16% 이다.
- 이 16% 에 해당하는 표준점수가 무엇인가를 묻는 질문이
qnorm(.32/2)혹은qnorm(.32/2, 0, 1) - 원점수일 경우에 대입해서 물어본다면
qnorm(.32/2, 100, 10)과 같이 하면 된다 (혹은 qnorm(.32/2, m.p1, sd.p1) ). - 위의 명령어에 대한 답은 우리가 가장 쉽게 이해한 방법에 의하면
- -1 혹은 90 이렇게 될 것이다.
- 하지만 위에서 봤던 것처럼 pnorm(1)-pnorm(-1)이 정확히
- 0.6826895 인 것처럼, 우리가 이해한 방법은 정확한 값을 구해주지는 않는다.
- 마찬가지로 qnorm(0.05/2)와 qnorm(1-(0.05/2))는
- 표준편차 값인 1이 왼쪽으로 두개 내려가고 오른 쪽으로 두개 올라간 값의 quotient값을 구하는 것이므로
- 즉, 위의 histogram에서 붉은 색 부분의 바깥 쪽 면적에 해당하는 점수를 물어보는 것이므로
- -2와 2라고 대답해도 되지만 정확한 답은 아래와 같다 (1.96).
> qnorm(0.05/2) [1] -1.959964 > qnorm(1-(0.05/2)) [1] 1.959964 >
- 이에 해당하는 원점수 (p1 원소에 해당하는) 값은 80과 120이 아니라 아래와 같을 것이다.
> qnorm(0.05/2, 100, 10) [1] 80.40036 > qnorm(1-(0.05/2), 100, 10) [1] 119.5996 >
> ################################ > hist(p1, breaks=50, col = rgb(1, 0, 0, 0.5), + main = "histogram of p1 and p2",) > abline(v=mean(p1), col="black", lwd=3) > hist(p2, add=T, breaks=50, col=rgb(0,0,1,.5)) > abline(v=mean(p2), col="violet", lwd=3) >
distribution of sample means
> s.size <- 10 > > means.temp <- c() > s1 <- sample(p1, s.size, replace = T) > mean(s1) [1] 99.64273 > means.temp <- append(means.temp, mean(s1)) > means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T))) > means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T))) > means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T))) > means.temp <- append(means.temp, mean(sample(p1, s.size, replace = T))) > means.temp [1] 99.64273 107.15516 103.81192 103.12311 105.88372 >
….
- s.size는 10으로 우선 고정하고
- 한 샘플을 취하여 그 평균값을 means.temp 메모리에 add한다 (저장하는 것이 아니라 means.temp에 붙힌다).
- 그 다음 샘플의 평균을 다시 means.temp에 저장한다
- 그 다음 . . . 모두 5번을 하고 출력을 해본다
> iter <- 1000000
> # means <- c()
> means <- rep(NA, iter)
> for (i in 1:iter) {
+ # means <- append(means, mean(sample(p1, s.size, replace = T)))
+ means[i] <- mean(sample(p1, s.size, replace = T))
+ }
> length(means)
[1] 1000000
> mean(means)
[1] 99.99544
> sd(means)
[1] 3.161886
> se.s <- sd(means)
>
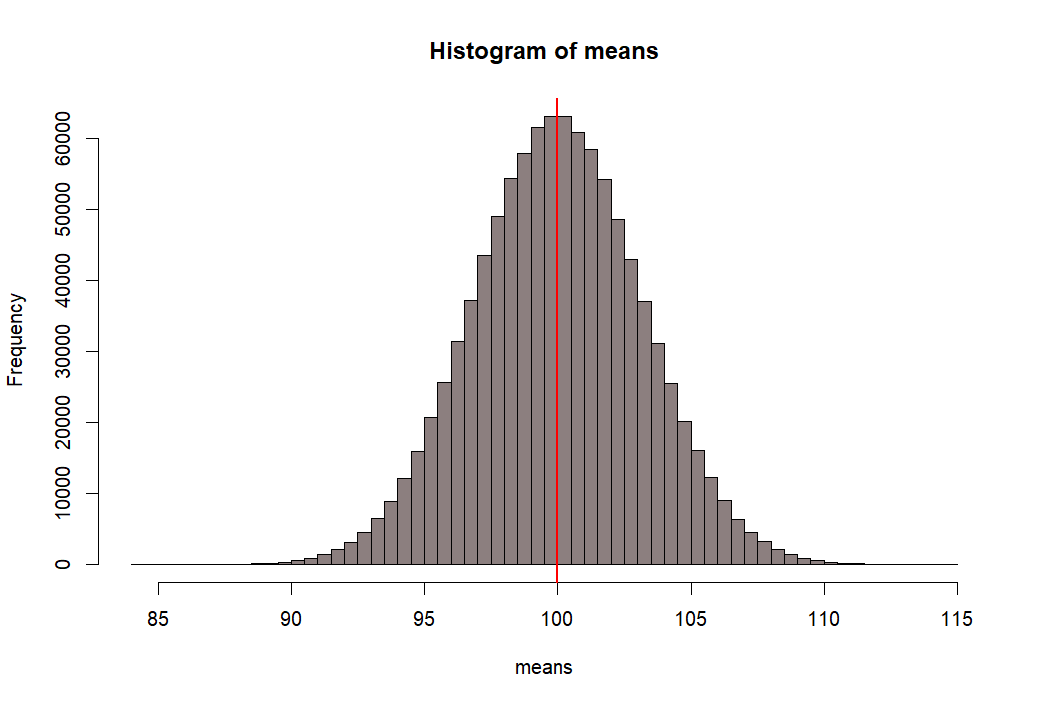
> hist(means, breaks=100, col=rgb(.1, 0, 0, .5))
> abline(v=mean(means), col="red", lwd=2)
>
….
> # now we want to get sd of this distribution
> lo1 <- mean(means)-se.s
> hi1 <- mean(means)+se.s
> lo2 <- mean(means)-2*se.s
> hi2 <- mean(means)+2*se.s
> lo3 <- mean(means)-3*se.s
> hi3 <- mean(means)+3*se.s
>
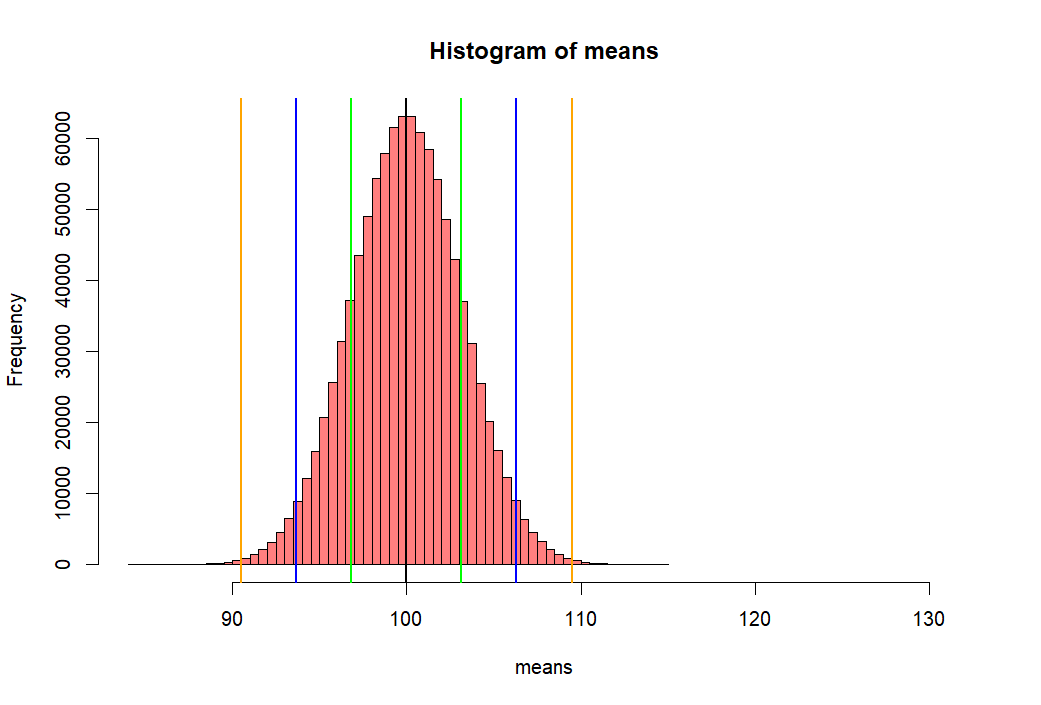
> hist(means,
+ xlim = c(mean(means)-5*sd(means), mean(means)+10*sd(means)),
+ col = rgb(1, 0, 0, .5))
> abline(v=mean(means), col="black", lwd=2)
> # abline(v=mean(p2), colo='darkgreen', lwd=3)
> abline(v=c(lo1, hi1, lo2, hi2, lo3, hi3),
+ col=c("green","green", "blue", "blue", "orange", "orange"),
+ lwd=2)
>
….
- 위 백만개의 샘플평균이 모인 집합의 히스토그램을 그리고
- 그 집합의 표준편차값을 수직선으로 표시하기 위해서
- mean(means) +- se.s 와 같은 방법을 쓴 후 그래프로 그린다.
- 아래에서 선 하나씩의 길이는 means 집합의 (distribution of sample means)
- 표준편차값이다.
- 이 표준편차 값을 위에서 sd(means)로 구한 후에 se.s로 저장한 적이 있다.
- 그리고 그 값은 3.161886 이었다.
> se.s [1] 3.161886
> # meanwhile . . . .
> se.s
[1] 3.161886
>
> se.z <- sqrt(var(p1)/s.size)
> se.z <- c(se.z)
> se.z
[1] 3.162278
>
> # sd of sample means (sd(means))
> # = se.s
>
> # when iter value goes to
> # unlimited value:
> # mean(means) = mean(p1)
> # and
> # sd(means) = sd(p1) / sqrt(s.size)
> # that is, sd(means) = se.z
> # This is called CLT (Central Limit Theorem)
> mean(means)
[1] 99.99544
> mean(p1)
[1] 100
> sd(means)
[1] 3.161886
> var(p1)
[,1]
[1,] 100
> sqrt(var(p1)/s.size)
[,1]
[1,] 3.162278
> se.z
[1] 3.162278
>
> sd(means)
[1] 3.161886
> se.s
[1] 3.161886
> se.z
[1] 3.162278
>
> # because CLT
> loz1 <- mean(p1)-se.z
> hiz1 <- mean(p1)+se.z
> loz2 <- mean(p1)-2*se.z
> hiz2 <- mean(p1)+2*se.z
> loz3 <- mean(p1)-3*se.z
> hiz3 <- mean(p1)+3*se.z
>
> c(lo1, loz1)
[1] 96.83356 96.83772
> c(lo2, loz2)
[1] 93.67167 93.67544
> c(lo3, loz3)
[1] 90.50978 90.51317
>
> c(hi1, hiz1)
[1] 103.1573 103.1623
> c(hi2, hiz2)
[1] 106.3192 106.3246
> c(hi3, hiz3)
[1] 109.4811 109.4868
>
>
….
- 그런데 이 값은 (se.s = 3.161886)
- se.z 를 구하는 방법과 거의 같은 값을 갖는다 3.162278
> se.z <- sqrt(var(p1)/s.size) > se.z <- c(se.z) > se.z [1] 3.162278
- 사실, 우리가 백만 번의 샘플을 취해서 구한 means 집합의 평균과 표준편차 값은
- 이것을 정확하게는 mean of the distribution of sample means,
- standard deviation of the distribution of sample means 라고 부른다
- 그리고 standard deviation of the distribution of sample means를 흔히
- standard error라고 부른다.
- script에서 se.s 그리고 se.z 와 같은 se를 쓴 이유도 standard error 값을 구한 것이기 때문이다.
- 만약에 백만 번이 아니라 무한 대로 더 큰 숫자를 사용한다고 하면
- 위의 se.z 값을 구하는 식의 값을 갖게 된다. 이것을 말로 풀어서 설명하면
- 샘플평균들의 집합에서 표준편차 값은
- 원래 모집단의 분산값을 샘플사이즈로 나누어준 값에 제곱근을 씌워서 구할 수 있다이다.
\begin{eqnarray*} \overline{X} \sim \displaystyle \text{N} \left(\mu, \dfrac{\sigma^{2}}{n} \right) \end{eqnarray*}
\begin{eqnarray} & & \text{Normal distribution of sample means.} \\ & & \mu_{\overline{X}} = \mu \\ & & (\sigma_{\overline{X}})^2 = \frac{\sigma^2}{n} \;\; \text{or} \;\; \sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}} \end{eqnarray}
see Central Limit Theorem and Sampling Distribution
- 즉, 샘플평균을 모은 집합의 분산값은 그 샘플이 추출된 원래 population의 분산값을 샘플크기로 (sample size) 나누어 준 값이다.
- 즉,
var(means) = var(p1) / s.size - 따라서,
std(means) = sqrt(var(p1) / s.size) - 더하여 그 샘플평균 집합의 평균 값은 population의 평균값이 된다
- 즉,
mean(means) = mean(p1)
- 따라서 lo, hi에 해당하는 means분포의 값을 mean(means) +- sd(means)로 구했었는데,
- 샘플평균의 분포를 무한대 번을 했다고 하면 사실 이 값은
- mean(p1) +- se.z 로 구하는 것이 정확할 것이다.
- 여기서
se.z = sqrt(var(p1)/s.size)) - loz1 - hiz1, loz2 - hiz2 값들은 이렇게 구한 값들이다.
참고
> lo1 <- mean(means)-se.s > hi1 <- mean(means)+se.s > lo2 <- mean(means)-2*se.s > hi2 <- mean(means)+2*se.s > lo3 <- mean(means)-3*se.s > hi3 <- mean(means)+3*se.s
> hist(means,
+ xlim = c(mean(means)-5*sd(means), mean(means)+10*sd(means)),
+ col = rgb(1, 0, 0, .5))
> abline(v=mean(means), col="black", lwd=2)
> # abline(v=mean(p2), colo='darkgreen', lwd=3)
> abline(v=c(lo1, hi1, lo2, hi2, lo3, hi3),
+ col=c("green","green", "blue", "blue", "orange", "orange"),
+ lwd=2)
>
> round(c(lo1, hi1))
[1] 97 103
> round(c(lo2, hi2))
[1] 94 106
> round(c(lo3, hi3))
[1] 91 109
>
> round(c(loz1, hiz1))
[1] 97 103
> round(c(loz2, hiz2))
[1] 94 106
> round(c(loz3, hiz3))
[1] 91 109
>
….
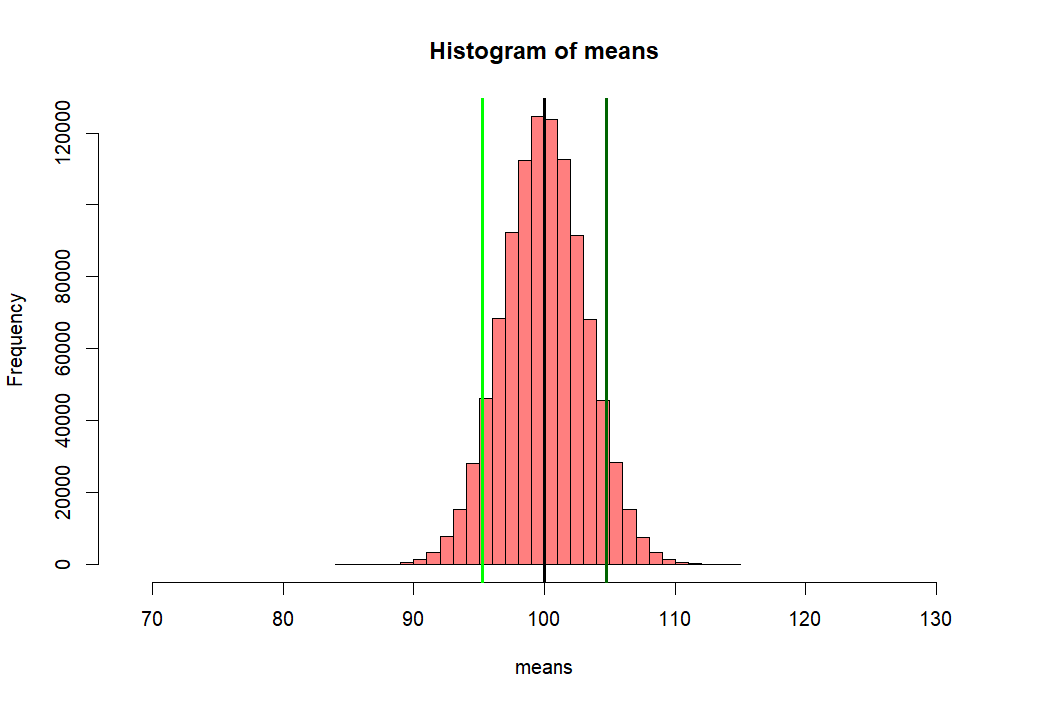
> m.sample.i.got <- mean(means)+ 1.5*sd(means) > m.sample.i.got [1] 104.7383 > > hist(means, + xlim = c(mean(means)-10*sd(means), mean(means)+10*sd(means)), + col = rgb(1, 0, 0, .5)) > abline(v=mean(means), col="black", lwd=3) > abline(v=m.sample.i.got, col='darkgreen', lwd=3) > > # what is the probablity of getting > # greater than > # m.sample.i.got? > m.sample.i.got [1] 104.7383 > pnorm(m.sample.i.got, mean(means), sd(means), lower.tail = F) [1] 0.0668072 > pnorm(m.sample.i.got, mean(p1), se.z, lower.tail = F) [1] 0.06701819 > > # then, what is the probabilty of getting > # greater than m.sample.i.got and > # less than corresponding value, which is > # mean(means) - m.sample.i.got - mean(means) > # (green line) > tmp <- mean(means) - (m.sample.i.got - mean(means)) > tmp [1] 95.26505 > abline(v=tmp, col='green', lwd=3) > 2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F) [1] 0.1339882 > m.sample.i.got [1] 104.7383 >
….
- 만약에 내가 한 샘플을 취해서 평균값을 살펴보니
- m.sample.i.got 값이었다고 하자 (104.7383).
- 이 값보다 큰 값이거나 아니면
- 이 값에 해당하는 평균 반대편 값보다 작은 값이 값이
- 나올 확률은 무엇인가?
- 즉, 녹색선과 연두색 선 바깥 쪽 부분의 probability 값은?
- 아래처럼 구해서 13.4% 정도가 된다
- 즉, 모집단 p1에서
- 무작위로 샘플링을 하여 (see sampling and probability sampling)
- s.size의 (10) 샘플을 취했는데 그 샘플의 평균이
- 104.7383 점보다 크거나 혹은
- 95.26505 점보다 작을 확률은 13.4% 이다.
> 2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F) [1] 0.1339882
Last one . . . Important
> ### one more time > mean(p2) [1] 120 > sd(p2) [1] 10 > sample(p2, s.size) [1] 120.9639 119.8341 134.0344 122.5446 121.4557 113.6820 114.7603 105.2138 122.7027 125.4131 > m.sample.i.got <- mean(sample(p2, s.size)) > m.sample.i.got [1] 120.2492 > > hist(means, + xlim = c(mean(means)-15*sd(means), mean(means)+15*sd(means)), + col = rgb(1, 0, 0, .5)) > abline(v=mean(means), col="black", lwd=2) > abline(v=m.sample.i.got, col='darkgreen', lwd=2) > > # what is the probablity of getting > # greater than > # m.sample.i.got? > m.sample.i.got [1] 120.2492 > pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F) [1] 7.560352e-11 > > # then, what is the probabilty of getting > # greater than m.sample.i.got and > # less than corresponding value, which is > # mean(means) - m.sample.i.got - mean(means) > # (green line) > tmp <- mean(means) - (m.sample.i.got - mean(means)) > abline(v=tmp, col='green', lwd=2) > 2 * pnorm(m.sample.i.got, mean(p1), sd(means), lower.tail = F) [1] 1.51207e-10 >
….
r/sampling_distribution.1757473121.txt.gz · Last modified: by hkimscil