x <- seq(20, 180, length=1000)
init <- dnorm(x, 100, 20)
plot(x, init, type="l", lwd=4, lty=1, xlab="x value",
ylab="Density", main="Scores with ~(100, sqrt(20))",
cex.main=2.5, cex.lab=2, cex.axis=2, col="red")
abline(v=40, lty=2, lwd=1)
abline(v=60, lty=2, lwd=1)
abline(v=80, lty=2, lwd=1)
abline(v=100, lty=2, lwd=1)
abline(v=120, lty=2, lwd=1)
abline(v=140, lty=2, lwd=1)
abline(v=160, lty=2, lwd=1)
axis(1, at=seq(20,160,10), lwd=2, cex.axis=2)
legend("topright", inset=.05, title="Score Dist.",
"mean=100, var=20", lwd=3, lty=1, col="black", cex=2)
This is an old revision of the document!
Variance
- 숫자로 측정된 한 변인이 (variable Y) 있다.
- 변인 Y는 총 100개의 원소로 구성되어 하나의 샘플이라고 할 수 있다.
- 변인 Y의 (그룹 Y의) 특징으로는 (sample statistics)
- 평균값이 50 이고
- 표준편차 값이 4 이다.
- 각 개인의 점수는
- 그룹의 특징이라고 할 수 있는 평균값과 (mean)
- 그룹의 특징을 제거한 랜덤하게 나타나는 차이값으로 (deviation score, difference score) 나타낼 수 있다.
- 가령 한 개인의 점수 54점에는 그룹의 특징인 50점과 그 그룹의 특징을 제외하고 나타나는 4점의 차이점수로 나눠진다.
- 따라서 변인 Y내의 모든 개인들의 점수는
- 그룹의 평균점수와
- 평균에서 랜덤하게 떨어져 있는 점수로 나누어 진다고 할 수 있다.
- 개인의 차이 점수를 모아서 보면 그 집합이 전체특징에서 (평균) 얼마나 멀리 떨어져 있는지를 (개인점수의 분포) 알려준다.
- 단 차이점수의 합은 언제나 0이 되므로 차이점수를 제곱해서 모아 본 점수를 가지고 “개인점수의 분포” 정도를 가늠한다.
- 위의 설명을 수식으로 요약하면 $ \sum{(Yi - \overline{Y})^2} $ 라고 쓸 수 있다.
- 우리는 이것을 Sum of Square 라고 (제곱의 합) 부른다.
- 그런데 위는 다음 처럼도 설명할 수 있다.
- 각 개인의 점수를 예측하라고 하면 평균값을 가지고 예측하는 것이 가장 오차가 적은 결과를 낳을 것을다.
- 따라서 개인의 점수를 평균으로 예측했을 때, 각 오차를 제곱해서 더해 보면 오차가 얼마나 큰지를 알려주는 지표가 된다.
- 이 때의 오차는 위의 설명과 마찬가지로 개인의 점수가 평균을 중심으로 얼마나 떨어져 있는지를 알려주는 지표가 된다.
- 따라서 먼저 언급한 제곱의 합은 “(평균으로 개인점수를 예측했을 때 얻는) 오차의 제곱의 합”이라고 이해라 수 있다.
- 이를 Sum of Square Error 라고도 부른다
- 혹은 Sum of Square Deviation Score 라고도 부르는데 deviation score라는 것은 개인 점수가 (Yi) 평균에서 얼마나 떨어져 있는가를 (deviated 되어 있는가) 알려준다고 설명하기 때문이다. 따라서 deviation score는 error score (from the mean) 와 같은 것이다.
- 또한 SS Error는 Sum of Square Residual이라고도 부른다. 여기서 residual의 의미는 샘플의 전체특징힌 평균값을 뺀 나머지라는 (residual) 뜻에서의 residual이다.
- 마지막으로 Sum of Square Total이라고도 부르는데 이 때 Total의 의미는 Y 변인의 (평균에서의) 오차 전체를 의미한다고 보면 된다.
- 분산은 (variance) 위의 Sum of Square 값을 (평균을 구할 때와 마찬가지로) 샘플의 크기인 n으로 나누어준 값을 말한다.
- 그런데 실제로는 n으로 나누어 주기 보다는 n-1로 나누어 주는데 흔히 이 n-1을 degrees of freedom이라고 부른다.
- 이에 대해서는 다른 부분에서 자세히 설명한다.
- 따라서 분산값은 아래처럼 요약된다.
\begin{eqnarray*} \sigma & = & \dfrac {\text{SS}} {\text{df}} \\ & = & \dfrac{\text{Sum of Error Square}}{\text{df}} \\ & = & \dfrac{\text{Sum of Residual Square}}{\text{df}} \\ & = & \dfrac{\text{Sum of DS Square}}{\text{df}}, \;\;\; \text{DS = Deviation Score} \\ & = & \dfrac{\sum{(Yi - \overline{Y})^2}}{n-1}, \;\;\; \text{where } (Yi - \overline{Y}) = \text{Error, Residual, or DS} \end{eqnarray*}
Mean,Mode,Median 등의 중심경향값과 더불어서 많이 사용되는 statistics(통계치)로는 데이터가 얼마나 퍼져 있는지 (spread)를 나타내는 것들이 있다. 가장 평이하고 이해하기 쉬운 개념으로는 range(범위)가 있으며, 다소 직관적이지는 않지만 여러가지 통계 계산에 사용되는 것으로는 Variance(분산)이 있다.
아래의 그래프는 각각 그 평균과 분산값이 다른 그래프이다. 검은색 라인의 경우 (가장 왼쪽), 평균은 -2, 분산값은 16 이고; 붉은 색 라인은 평균이 5, 분산값은 4, 마지막으로 청색 라인의 경우는 평균은 8, 분산 값은 1 인 경우이다.
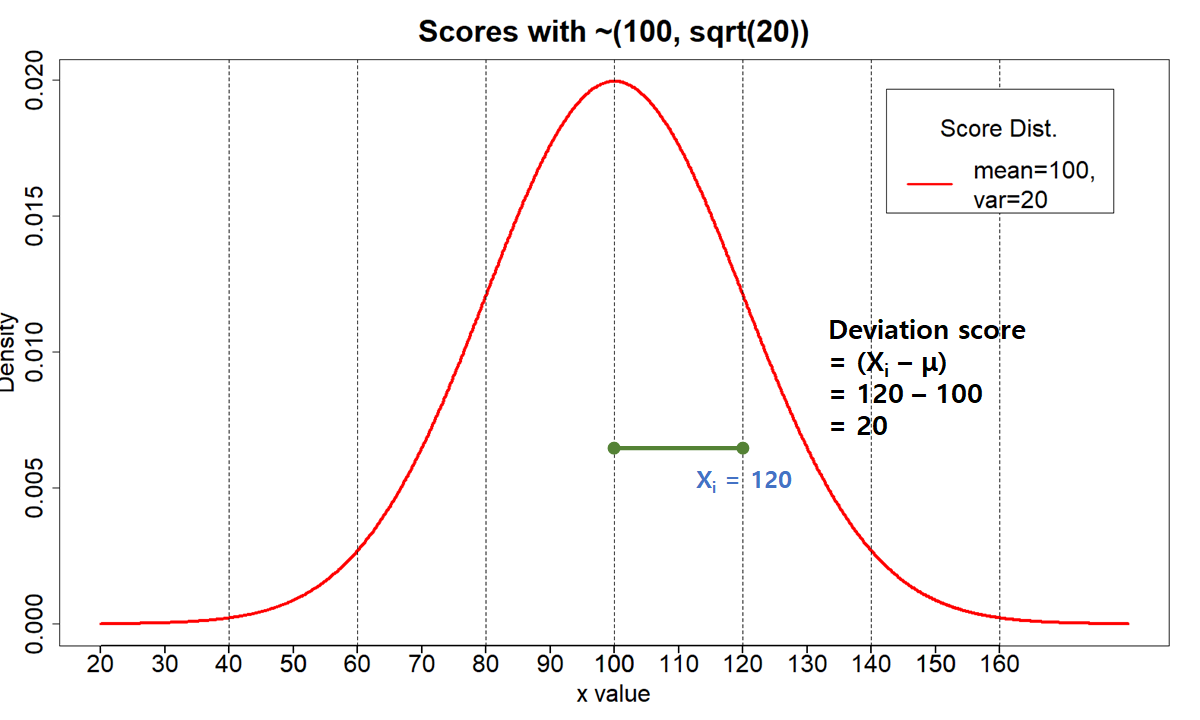
그림에서 직관적으로 보고 알 수 있듯이 분산은 그래프의 분포가 평균을 중심으로 얼마나 퍼져있는지를 (spread) 나타내주는 일종의 지표이다. 어떤 집합이 평균을 중심으로 얼마나 퍼져 있는가를 알아보기 위한 방법으로는 상식적으로 떠올릴 수 있는 것은 각 개인의 점수가 평균에서 얼마나 떨어져 있는가를 측정하여 모두 더한 후 이를 개인 수로 (number of elements) 나누는 방법을 떨올릴 수 있다. 개인의 점수가 평균에서 얼마나 떨어져 있는가를 deviation score라고 한다. 아래의 그래프는 평균이 100인 그래프를 그린 것인데, 어느 한 개인의 점수가 120이라고 하면 그 개인의 deviation score는 120-100, 즉 20이라고 할 수 있다.
개인의 deviation score를 모두 더하는 것은 아래의 수식으로 표현할 수 있다. 즉, 어떤 집합의 개인의 숫자가 N이라고 하고, 각 개인을 X,,i,, 로 나타낼 때, deviation score의 합은 아래와 같다.
$$\text{Sum of Deviation Score} = \displaystyle \sum\limits_{i=1}^n ({X_i-\mu})$$
이를 집합을 이루는 개인의 숫자인 n으로 나누면 다음과 같이 표현할 수 있다.
$$\text{Average of Deviation Score} = \displaystyle \frac{\displaystyle \sum\limits_{i=1}^N ({X_i-\mu})}{N}$$
이렇게 하면 “개인들의 점수가 평균에서 얼마나 떨어져 있는지를 종합적으로 나타내 주는 지수가 될 수 있는것 처럼 보인다. 그러나, 이 방법의 문제는 deviation score의 합은 언제나 0이라는 점에 있다. 즉, 어떤 집합이든지 분산값을 위와 같이 구하려고 한다면, 그 분자 값은 언제나 0이 된다. 사실 평균이 하는 역할 중의 하나는 바로 각 개인의 수치의 무게중심을 찾아 주는 역할이므로 이와 같은 결과가 당연하다. 아래는 이를 나타내 주는 예이다.
| X | score | deviation score |
| X1 | 3 | 3-4=-1 |
| X2 | 4 | 4-4=0 |
| X3 | 3 | 3-4=-1 |
| X4 | 4 | 4-4=0 |
| X5 | 6 | 6-4=2 |
| total | 20 | 0 |
| Mean | 4 | |
| n | 5 |
deviation score의 합을 구하기 전에 각 deviation score의 값을 제곱을 하여 주면 이와 같은 결과를 방지할 수 있는데, 이를 수식으로 표현하면 아래와 같다.
$$\displaystyle \frac{\displaystyle \sum_{i=1}^N (X_i-\mu)^2}{N}$$
분산 값은 위와 같은 방법을 이용하여 구하게 된다. 따라서,
$$Var[X] = \sigma^2= \displaystyle \frac{\displaystyle \sum_{i=1}^N (X_i-\mu)^2}{N}$$
이를 우리나라 말로 옮기자면,
- “X 변인의 분산값은 X 변인의 각 개체값에서 평균값을 뺀 수의 제곱을 모두 더한 후, 이를 개체 수인 `n`으로 나누어 주어서 구한다” 라고 읽는다.
- 혹은 위 분포의 분산값은 deviation score를 제곱한 값을 모두 더한 값을 N으로 나눈 값이다. 라고 읽는다.
- 수학자들은 위의 “deviation score를 제곱한 값을” “Sum of Square 값이라고도” 부르며 이를 종종 “SS”로 줄여서 쓴다. 따라서, 분산값은 SS 값을 N으로 나누어 준 값을 말한다고도 한다.
- 마지막으로 위의 분산값이 갖는 의미를 이렇게도 이야기할 수 있다.
- 어느 정상분포의 (normal distribution) 평균을 알고 있다고 하자.
- 만약에 당신이 각 분포내 각 개인의 값을 예측해야 한다고 할 때, 가장 오차가 작은 예측값을 대는 방법은 평균값으로 예측 값을 쓰는 것이다. 따라서, SS 값은 (평균값으로 개인의 점수를 예측했을 때 발생하는 개인) 오차의 제곱의 합을 의미하며, 이 오차의 제곱합을 N으로 나눈 값이 분산값이다. 이는 현재로서는 중요하지 않지만, 후에 correlation과 regression을 배울 때 유용한 개념이므로 이해해 두도록 한다.
따라서 위의 보기에서 들었던 X 변인의 집합에서 분산 값은 1.5이다.
| X | score | deviation score | squared value |
| X1 | 3 | 3-4=-1 | 1 |
| X2 | 4 | 4-4=0 | 0 |
| X3 | 3 | 3-4=-1 | 1 |
| X4 | 4 | 4-4=0 | 0 |
| X5 | 6 | 6-4=2 | 4 |
| total | 20 | 0 | 6 |
| Mean, Variance | 4 | 6/4 = 1.5 | |
| n | 5 | 5 |
note: You guess each value with the mean value of the X note: which means "error" note: therefore, sum of square value of error is SS part
다른 공식
분산의 공식을 5명으로 이루어진 집합에 사용하는 것은 큰 무리가 없지만, 100명으로 이루어진 집합에 적용하는 것은 손이 많이 간다는 단점이 있다. 따라서, 위의 분산 공식을 변형한 공식을 쓰기도 하는데, 형식만 다를 뿐이지 똑같은 공식이다.
$ \sigma^2 = \displaystyle \frac{\displaystyle \sum (X_i-\mu)^2}{N}$ 에서
\begin{eqnarray*} \sum (X_i-\mu)^2 & = & \sum [(X_i^2)-(2*X_i*\mu)+(\mu^2)] \\ & = & \sum (X_i^2) - \sum (2*X_i*\mu) + \sum (\mu^2) \\ & = & \sum (X_i^2) - 2 \mu \sum (X_i) + N (\mu^2) \\ & = & \sum (X_i^2) - 2 \mu (N * \mu) + N (\mu^2) \\ & = & \sum (X_i^2) - N * \mu^2 \end{eqnarray*}
위에서, $\text{2 and}$ $\mu$ $\text{are constants. }$
\begin{eqnarray*} \displaystyle \mu & = \displaystyle \frac{\sum (X_i)}{N} \\ \displaystyle \sum (X_i) & = \displaystyle N * \mu \\ \end{eqnarray*}
따라서 분산값은 아래의 공식으로도 구할 수 있다2).
\begin{eqnarray} \sigma^2 & = & \displaystyle \frac{\sum (X_i^2) - N * \mu^2}{N} \nonumber \\ & = & \displaystyle \frac{\sum (X_i^2)}{N} - \mu^2 \end{eqnarray}
분산값이 크고 작고가 의미하는 것은 그 집합의 분포가 평균을 중심으로 얼마나 넓게 퍼져 있는가를 나타내 준다는 것이다. 만약에 분산 값이 크다면 그 집합의 분포가 평균을 중심으로 넓게 퍼져있음을 의미한다.
Read more
샘플의 분산으로 모집단의 분산값을 추정할 때에는, 샘플의 숫자인 $n$ 대신에 $n-1$ 을 사용한다 (참조. estimated standard deviation). 샘플의 분산은 $s^2$ 을 기호로 사용한다.
$ s^2 = Var[X] = \displaystyle \frac{\displaystyle \sum_{i=1}^n (X_i - \overline{X})^2}{n-1}$
위에서 언급한 것처럼, 분산 공식의 분자부분을 Sum of Squares라고 부르고 줄여서 $SS$라고 쓰고, n-1을 degrees of freedom 혹은 이를 줄여서 $df$라고 쓴다. 따라서 위의 분산을 구하는 식은 아래와 같이 표현될 수 있다.
$$s^2 = \displaystyle \frac{SS}{df}$$
위에서 샘플의 분산으로 모집단의 분산을 추정할 때 n-1을 쓴다고 하였지만, 사실은 모집단의 분산을 계산할 때에도 n-1을 쓴다. 그 이유는 모집단이라면 N이 상당히 클텐데, 이 경우 SS값도 아주 큰 값을 갖는다. 이 숫자을 (SS값을) N으로 나누거나 N-1로 나누거나 큰 차이가 없다. 따라서 모든 경우에 n-1로 나누어 분산을 구한다.
$$\sigma^2 = \displaystyle \frac{SS}{N-1} = \displaystyle \frac{SS}{df}$$
아래는 R에서 보는 간단한 예이다.
> a <- rnorm2(100000000, 100, 10) > a.mean <- mean(a) > ss <- sum((a-a.mean)^2) > n <- length(a) > df <- n-1 > ss/n [1] 100 > ss/df [1] 100
See also Standard Deviation