Table of Contents
Calculating Probability
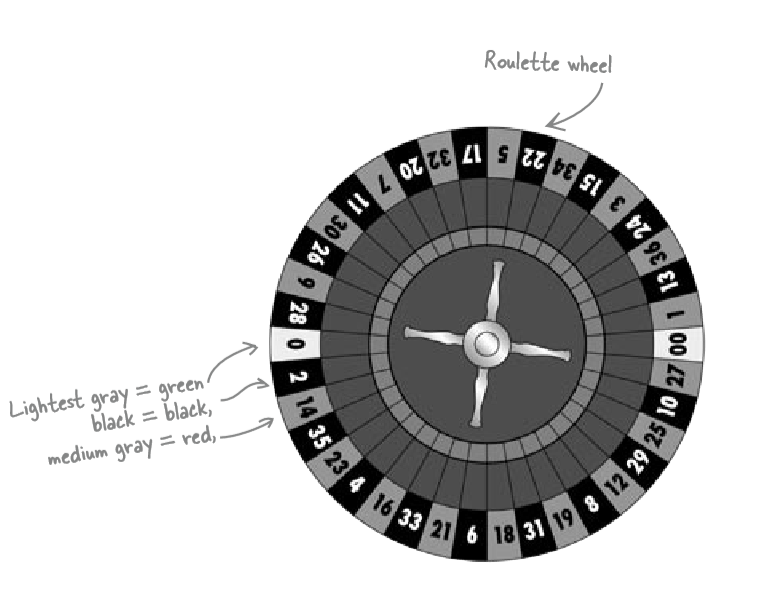
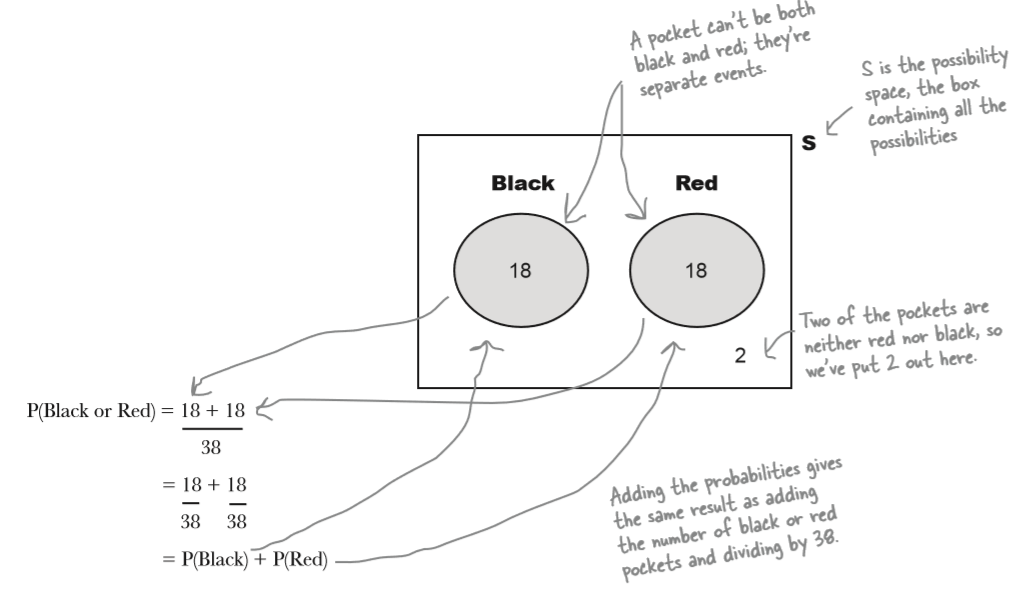
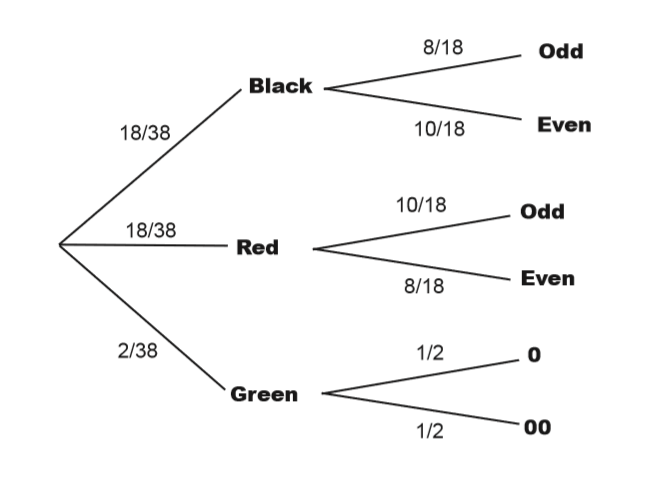
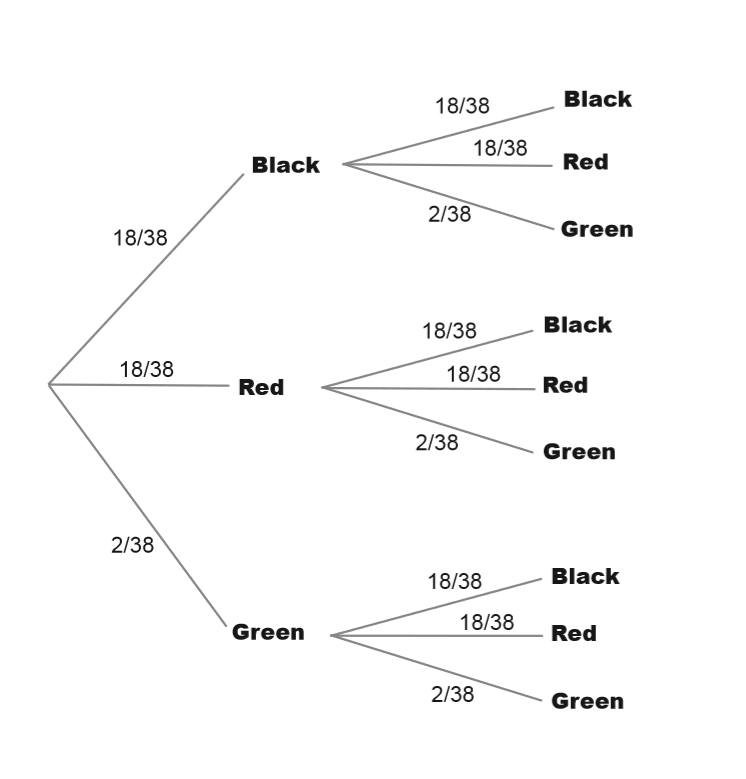
How many pockets (holes) are there? 38
. . .
- black = 18 blacks, consisted with
- 8 odd numbers and
- 10 even numbers
- medium grey part = red, consisted with
- 10 odd numbers and
- 8 even numbers
- white (almost) = green, consisted with
- O and
- OO
- #s = numbers (odd and even to 36, plus O, OO)
$$P(A) = \frac {n(A)}{n(S)} $$
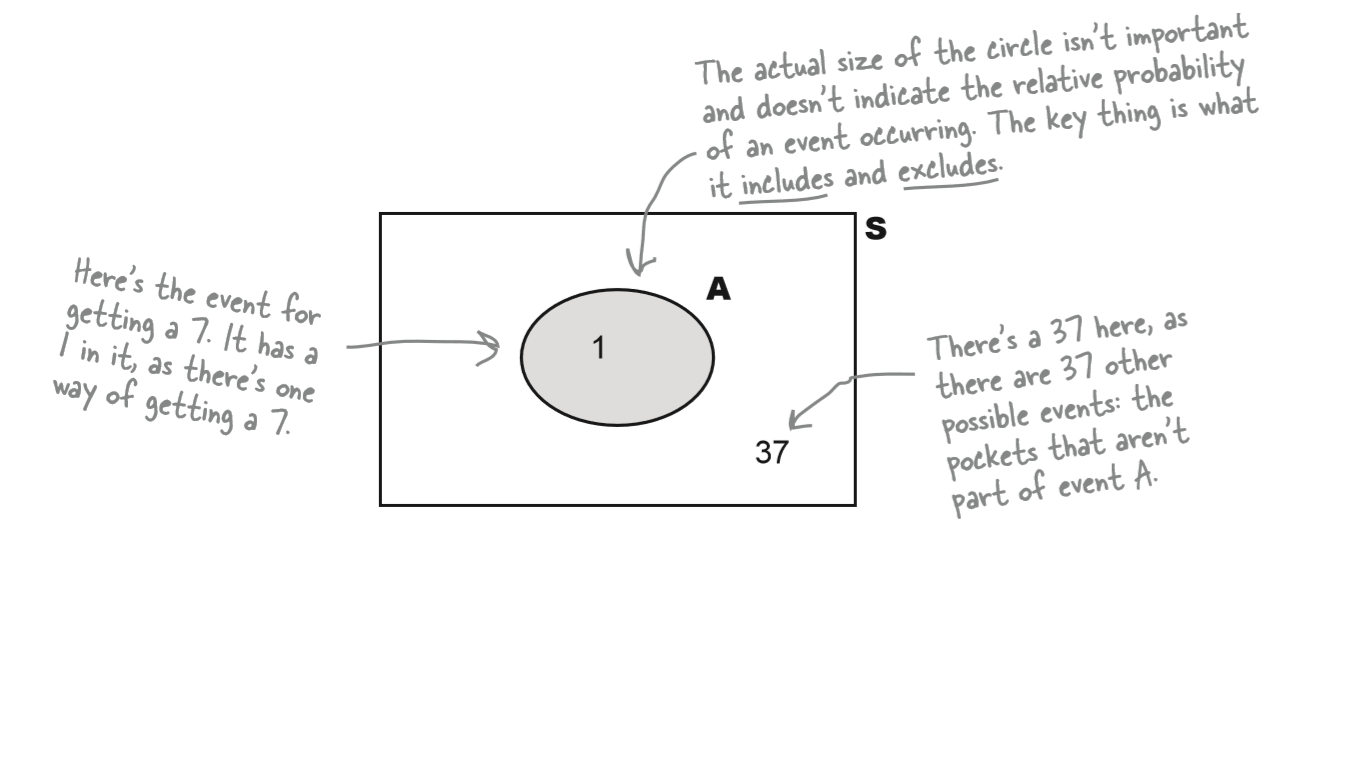
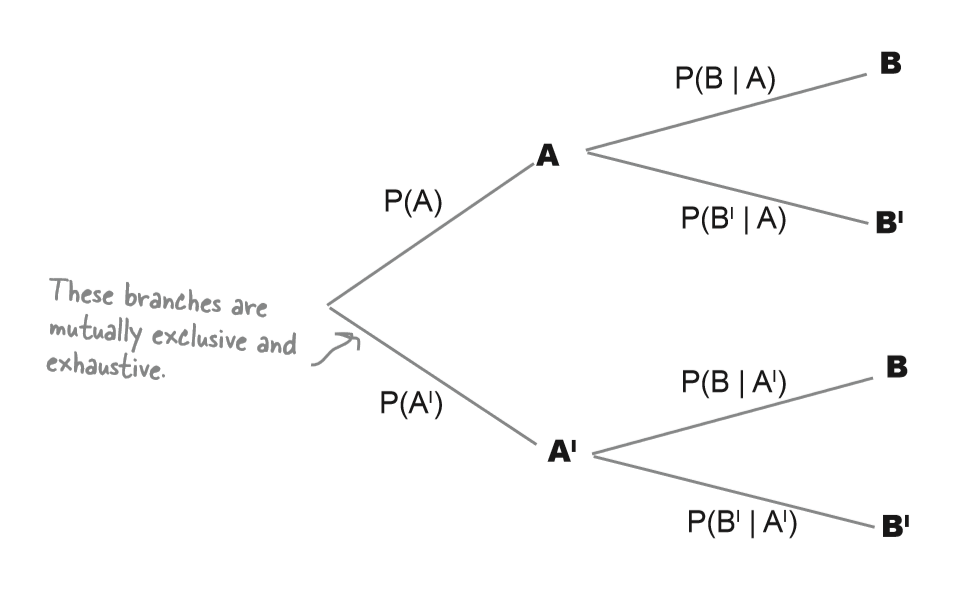
Probability of event A happening:
S = space S
A = event A
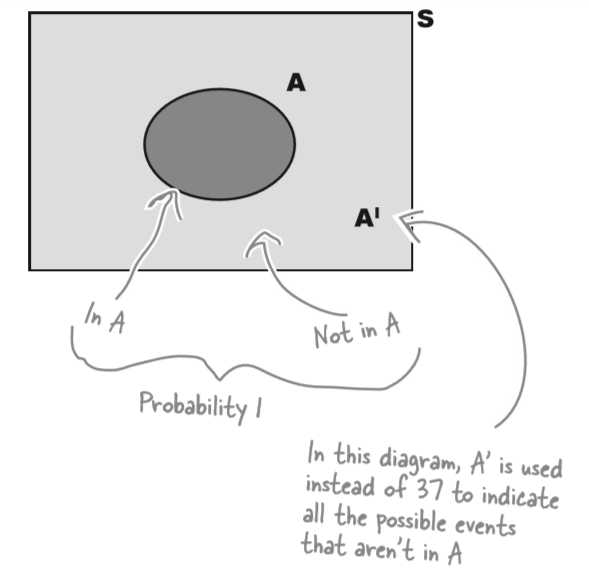
$$ P(A) + P(A') = 1 $$
$$ P(A') = 1 - P(A) $$
$ P(9) $
$ P(Green) $
$ P(Black) $
$ P(38) $
\begin{eqnarray*} P(\text{Green}) & = & 2 / 38 \\ & = & 0.052632 & = & 0.053 \end{eqnarray*}
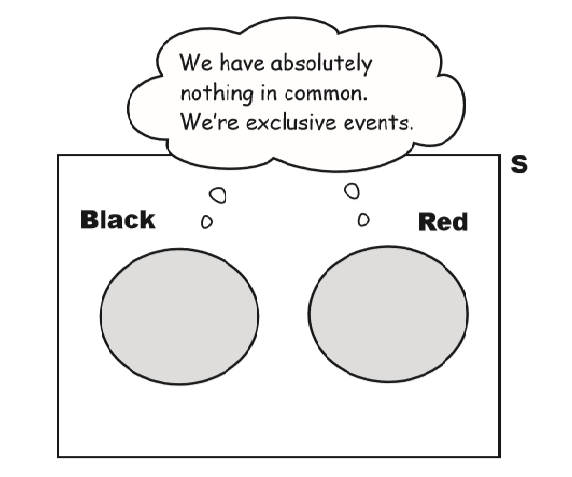
\begin{eqnarray*} P(\text{Black or Red}) & = & P(\text{Green'}) \\ & = & 1 - P(Green) \\ & = & 1 - 0.053 \\ & = & 0.947 \end{eqnarray*}
\begin{eqnarray*} P(\text{Black or Red}) & = & P(\text{B} \cup \text{R}) \\ & = & P(B) + P(R) \\ & = & \frac {18 + 18} {38} \\ & = & \frac {36}{38} \\ & = & 0.947 \end{eqnarray*}
{{:b:head_first_statistics:pasted:20190924-180111.png}}
{{:b:head_first_statistics:pasted:20190924-180227.png}}
{{:b:head_first_statistics:pasted:20190924-180416.png}}
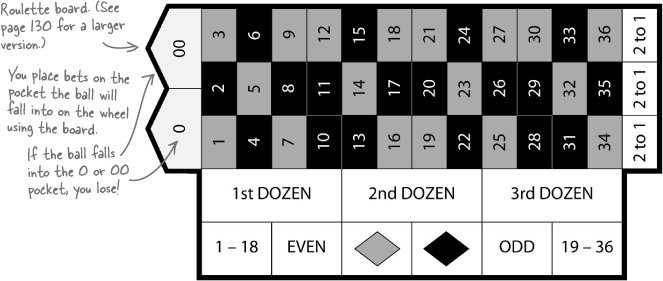
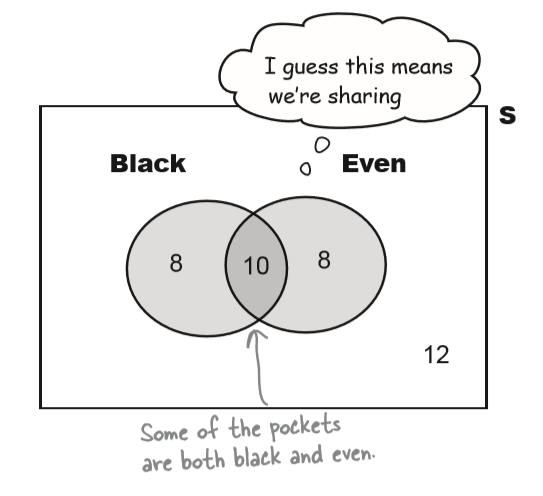
Let’s find the probability of getting a black or even (assume 0 and 00 are not even).
- What’s the probability of
- getting a black?
- What’s the probability of getting an even number?
- What do you get if you add these two probabilities together?
- Finally, use your roulette board to count all the holes that are either black or even, then divide by the total number of holes. What do you get?
- Intersection $ \cap $
- Union $\cup $
- $P(A \cup B) = P(A) + P(B) - P(A \cap B)$
음영으로 해당 영역을 표시하시오.
$P(A \cap B) + P(A \cap B')$
$ P(A' \cap B') $
$ P(A \cup B) - P(B) $
probability of A given B
$ P(A \vert B) $ : The probability of A given that we know B has happened
$ P(A \vert B) = \displaystyle \frac {P(A \cap B)}{P(B)} $
$ P(A \cap B) = P(B \cap A) $
$ P(A \cap B) = P(A \vert B) * P(B) $
$ P(B \cap A) = P(B \vert A) * P(A) $
Hence,
$ P(A \vert B) * P(B) = P(B \vert A) * P(A) $
Because we’re trying to find the probability of A given B, we’re only interested in the set of events where B occurs.
Note that
\begin{eqnarray*}
P(A \vert B) & = & \frac {\text{black}}{\text{black + grey}} \\
& = & \frac {P(A \cap B)}{P(B)}
\end{eqnarray*}
\begin{eqnarray*} P(A \cap B) & = & {\text{black}} \end{eqnarray*}
[
]
[
]
….
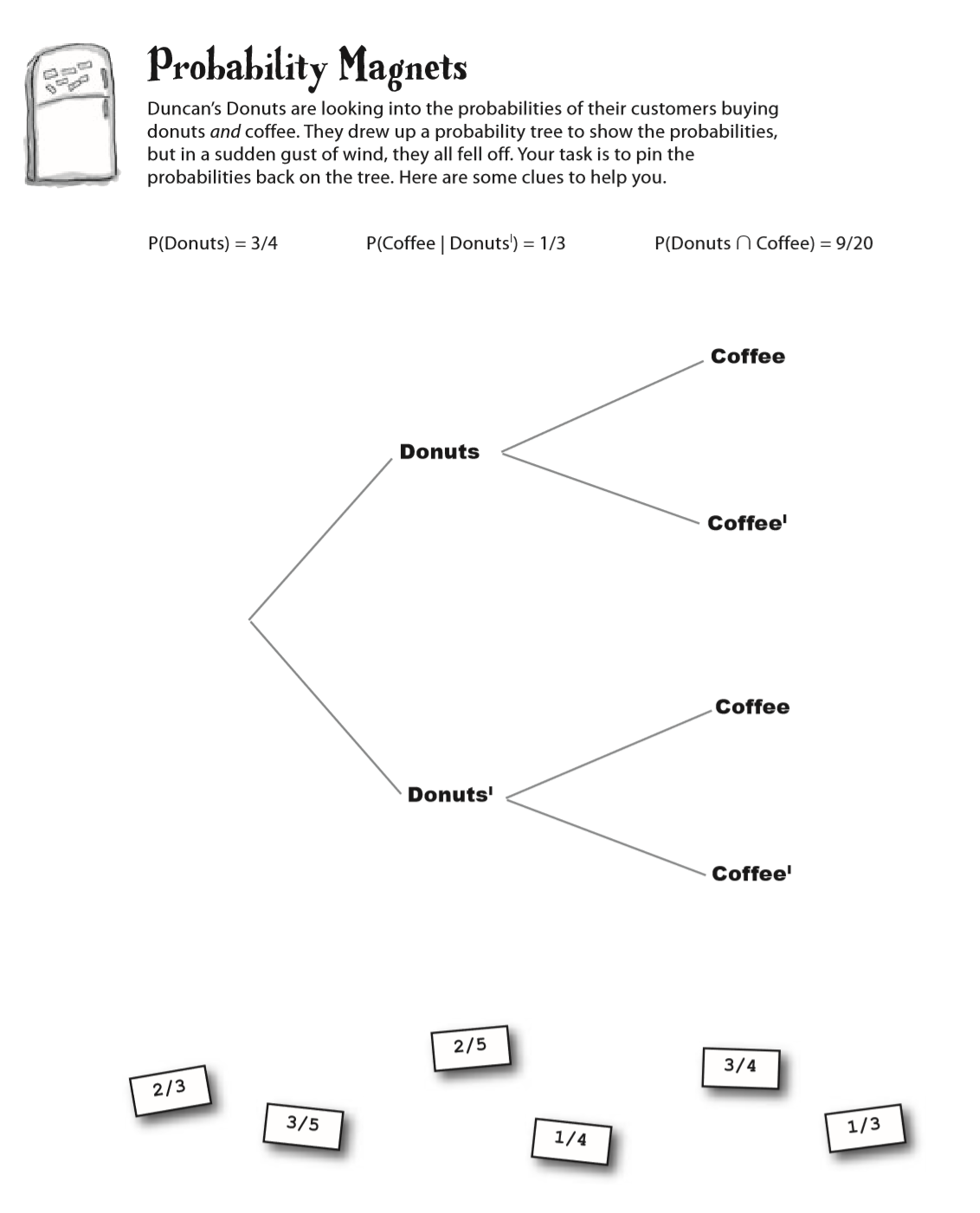
Probability magnet
Duncan’s Donuts are looking into the probabilities of their customers buying donuts and coffee. They drew up a probability tree to show the probabilities, but in a sudden gust of wind, they all fell off. Your task is to pin the probabilities back on the tree. Here are some clues to help you.
- P(Donuts) = 3/4
- P(Coffee | Donuts') = 1/3
- P(Donuts ∩ Coffee) = 9/20
3/4, 1/4, 2/5, 3/5, 1/3, 2/3
[
]
[
]
- P(Donuts')
- P(Donuts' ∩ Coffee)
- P(Coffee' | Donuts)
- P(Coffee)
- P(Donuts | Coffee)
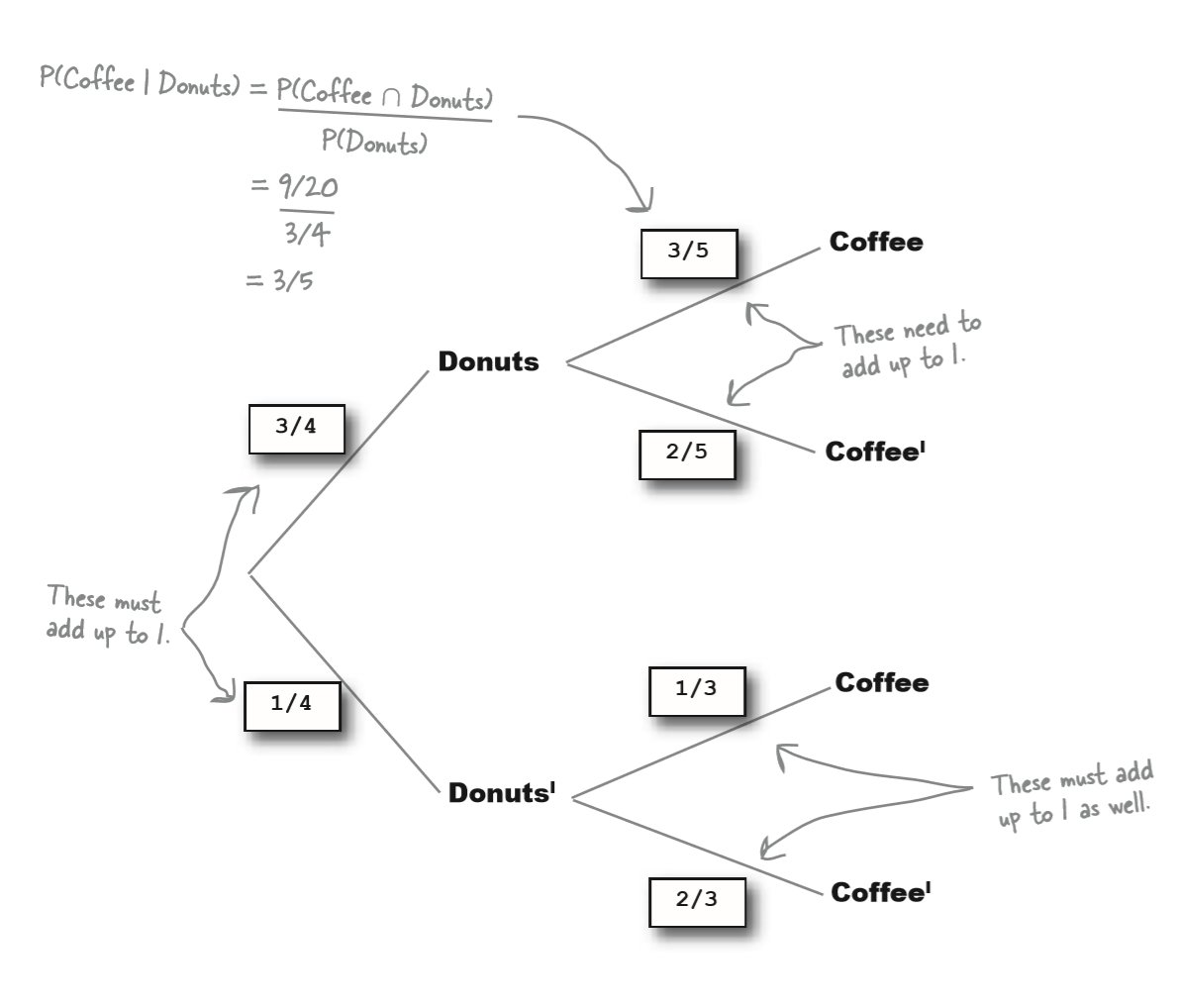
d (3/4) -- c [x = 3/5] [k = p(c and d)]
-- ~c [y = 2/5]
~d (1/4) -- c (1/3) --> [a = p(c and ~d)]
-- ~c [2/3]
x * 3/4 = p(d and c) = 9/20
x = 9/20 * 4/3
= 36/60
= 6/10 = 3/5
P(~d ∩ c) = a = 1/4 * 1/3 = 1/12
P(c) = k + a
k = 3/4 * 3/5 = 9/20
a = 1/12
P(c) = 54/120 + 10/120 = 64/120 = 16/30 = 8/15
c (8/15) -- d [j]
-- ~d
~c (7/15)
j = p(d | c)
p(d and c) = 9/20 이므로
8/15 * j = 9/20
j = 9/20 * 15/8 = 9/4 * 3/8 = 27/32
Q: I still don’t get the difference between P(A ∩ B) and P(A | B).
A: P(A ∩ B) is the probability of getting both A and B. With this probability, you can make no assumptions about whether one of the events has already occurred. You have to find the probability of both events happening without making any assumptions. P(A | B) is the probability of event A given event B. In other words, you make the assumption that event B has occurred, and you work out the probability of getting A under this assumption.
Q: So does that mean that P(A | B) is just the same as P(A)?
A: No, they refer to different probabilities. When you calculate P(A | B), you have to assume that event B has already happened. When you work out P(A), you can make no such assumption.
Q: Is P(A | B) the same as P(B | A)? They look similar.
A: It’s quite a common mistake, but they are very different probabilities. P(A | B) is the probability of getting event A given event B has already happened. P(B | A) is the probability of getting event B given event A occurred. You’re actually finding the probability of a different event under a different set of assumptions.
Q: Are probability trees better than Venn diagrams?
A: Both diagrams give you a way of visualizing probabilities, and both have their uses. Venn diagrams are useful for showing basic probabilities and relationships, while probability trees are useful if you’re working with conditional probabilities. It all depends what type of problem you need to solve.
Q: Is there a limit to how many sets of branches you can have on a probability tree?
A: In theory there’s no limit. In practice you may find that a very large probability tree can become unwieldy, but you may still find it easier to draw a large probability tree than work through complex probabilities without it.
Q: If A and B are mutually exclusive, what is P(A | B)?
A: If A and B are mutually exclusive, then P(A ∩ B) = 0 and P(A | B) = 0. This makes sense because if A and B are mutually exclusive, it’s impossible for both events to occur. If we assume that event B has occurred, then it’s impossible for event A to happen, so P(A | B) = 0.
Swap the order of buying. What do you get?
...
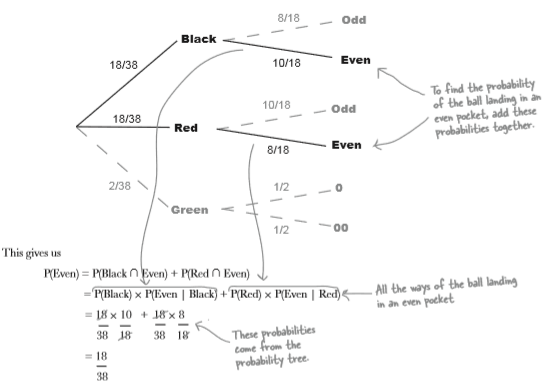
Maybe we can win some chips back with another bet. This time, the croupier says that the ball has landed in an even pocket. What’s the probability that the pocket is also black?
$$ P(Black \vert Even) = \frac {P(Black \cap Even)}{P(Even)} $$
Step 1: Finding P(Black ∩ Even)
\begin{eqnarray*}
P(Black \cap Even)
& = & \frac {18}{38} * \frac {10}{18} \\
& = & \frac {10}{38} \\
P(Black \vert Even) & = & \frac {P(Black \cap Even)}{P(Even)} \\
P(Black \cap Even) & = & P(Black) * P(Even \vert Black) \\
P(Black \vert Even) & = & \frac{P(Black) * P(Even \vert Black)} {P(Even)}
\end{eqnarray*}
Step 2: Finding P(Even)
\begin{eqnarray*} P(Even) & = & P(Black \cap Even) + P(Red \cap Even) \\ & = & P(Black) * P(Even \vert Black) + P(Red) * P(Even \vert Red) \\ & = & \frac{18}{38} * \frac{10}{18} + \frac{18}{38} * \frac{8}{18} \\ & = & \frac{18}{38} \\ & = & \frac{9}{19} \end{eqnarray*}
Step 3: Finding P(Black l Even)
$$ P(Black \vert Even) = \frac {P(Black \cap Even)} {P(Even)} $$
We started off by finding an expression for P(Black ∩ Even)
\begin{eqnarray*}
P(Black \cap Even) & = & P(Even \cap Black) \\
& = & P(Black) * P(Even \vert Black)
\end{eqnarray*}
After that we moved on to finding an expression for P(Even), and found that
$$ P(Even) = P(Black) * P(Even \vert Black) + P(Red) * P(Even \vert Red) $$
Putting these together means that we can calculate P(Black | Even) using probabilities from the probability tree
\begin{eqnarray*} P(Black \vert Even) & = & \frac {P(Black \cap Even)}{P(Even)} \\ & = & \frac { P(Black) * P(Even \vert Black)}{P(Black) * P(Even \vert Black) + P(Red) * P(Even \vert Red)} \\ & = & \frac{5}{19} / \frac{9}{19} \\ & = & \frac{5}{19} * \frac{19}{9} \\ & = & \frac{10}{18} \\ \end{eqnarray*}
Think backward again
Draw a tree line for Odd, Even, Green probability first, then Black and White.
Bayes' Theorem
Bayes' Theorem
Generalization
$$P(A \vert B) = \frac {P(A \cap B)}{P(B)} $$
First,
$$ P(A \cap B) = P(A) * P(B \vert A) $$
For an easy way to understand, take a look at the tree.
Then, find P(B),
IF we take a look at the picture,
$$ P(B) = P(A) * P(B \vert A) + P(A') * P(B \vert A') $$
Hence, the answer is:
$$P(A \vert B) = \frac {P(A \cap B)}{P(B)} $$
$$P(A \vert B) = \frac {P(A) * P(B \vert A)}{P(A) * P(B \vert A) + P(A') * P(B \vert A')} $$
This is called “Bayes' Theorem”
e.g.
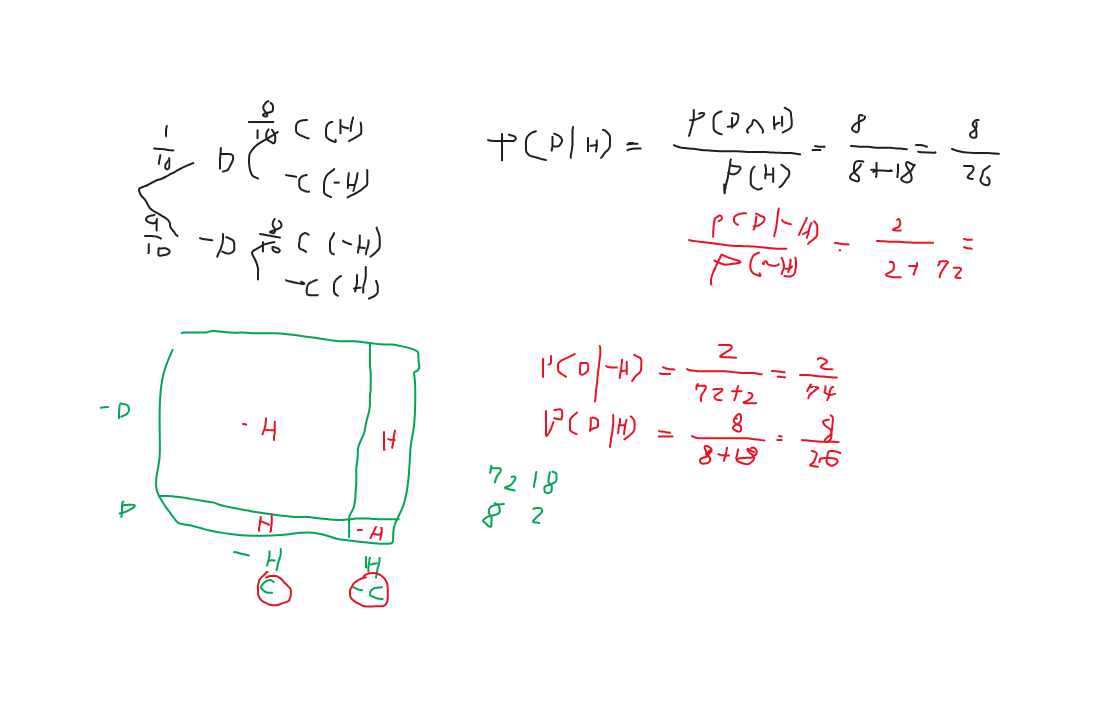
The Manic Mango games company is testing two brand-new games. They’ve asked a group of volunteers to choose the game they most want to play, and then tell them how satisfied they were with game play afterwards. 80 percent of the volunteers chose Game 1, and 20 percent chose Game 2. Out of the Game 1 players, 60 percent enjoyed the game and 40 percent didn’t. For Game 2, 70 percent of the players enjoyed the game and 30 percent didn’t. Your first task is to fill in the probability tree for this scenario.
Manic Mango selects one of the volunteers at random to ask if she enjoyed playing the game, and she says she did. Given that the volunteer enjoyed playing the game, what’s the probability that she played game 2? Use Bayes’ Theorem.
Dependent and Independent event
$P(E|B) = 10 /18$
$P(E) = 18 / 38$
if $P(E|B) \ne P(E)$ true,
then the two events are dependent.
$P(B) = 18 / 38$
$P(B|B) = 18 / 38$
If $P(A|B) = P(A)$ is true,
then the two events are independent.
$ P(\text{A} \vert \text{B}) = \displaystyle \frac {P(\text{A} \cap \text{B})}{P(\text{B})} $ 이므로
그리고, 만약에 위가 참이라면
$ P(A) = \displaystyle \frac {P(A \cap B)}{P(B)} $
따라서,
$ P(A \cap B) = P(A) * P(B) $
The Head First Health Club prides itself on its ability to find a class for everyone. As a result, it is extremely popular with both young and old. The Health Club is wondering how best to market its new yoga class, and the Head of Marketing wonders if someone who goes swimming is more likely to go to a yoga class. “Maybe we could offer some sort of discount to the swimmers to get them to try out yoga.” The CEO disagrees. “I think you’re wrong,” he says. “I think that people who go swimming and people who go to yoga are independent. I don’t think people who go swimming are any more likely to do yoga than anyone else.” They ask a group of 96 people whether they go to the swimming or yoga classes. Out of these 96 people, 32 go to yoga and 72 go swimming. 24 people are exceptionally eager and go to both. So who’s right? Are the yoga and swimming classes dependent or independent?
- Throwing a coin and getting heads twice in a row.
- Removing socks from a drawer until you find a matching pair.
- 양말을 한 짝 꺼낸 후, 다시 넣지 않았으므로 다음 양말을 꺼낼 때의 확률이 달라지게 됨. 따라서, 종속된 이벤트.
- Choosing chocolates at random from a box and picking dark chocolates twice in a row.
- Choosing a card from a deck of cards, and then choosing another one.
- Choosing a card from a deck of cards, putting the card back in the deck, and then choosing another one.
- The event of getting rain given it’s a Thursday
- 목요일이라고 해서 비가 오거나 오지 않을 확률이 낮아지거나 높아지지 않음
The Absent-Minded Diners
Three absent-minded friends decide to go out for a meal, but they forget where they’re going to meet. Fred decides to throw a coin. If it lands heads, he’ll go to the diner; tails, and he’ll go to the Italian restaurant. George throws a coin, too; heads, it’s the Italian restaurant; tails, it’s the diner. Ron decides he’ll just go to the Italian restaurant because he likes the food.
What’s the probability all three friends meet?
What’s the probability one of them eats alone?
- The probability of the ball having landed on the number 17 given the pocket is black.
- The probability of the ball landing on pocket number 22 twice in a row.
- The probability of the ball having landed in a pocket with a number greater than 4 given that it’s red.
- The probability of the ball landing in pockets 1, 2, 3, or 4.
https://youtu.be/NIqeFYUhSzU?t=904
https://youtu.be/NIqeFYUhSzU?t=1296
https://youtu.be/NIqeFYUhSzU?t=2550
