Table of Contents
Geometric Distribution
기하분포
\begin{align*}
\text{Geometric Distribution: } \;\;\; \text{X} & \thicksim Geo(p) \\
p(X = k) & = q^{k-1} \cdot p \\
E\left[ X \right] & = \frac{1}{p} \\
V\left[ X \right] & = \frac{q}{p^2} \\
\\
\end{align*}
Geometric Distributions
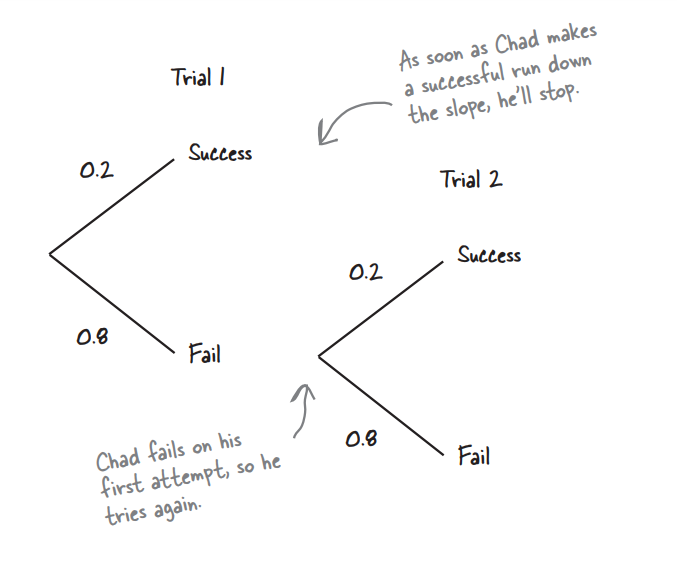
The probability of Chad making a clear run down the slope is 0.2, and he's going to keep on trying until he succeeds. After he’s made his first successful run down the slopes, he’s going to stop snowboarding, and head back to the lodge triumphantly
It’s time to exercise your probability skills. The probability of Chad making a successful run down the slopes is 0.2 for any given trial (assume trials are independent). What’s the probability he’ll need two trials? What’s the probability he’ll make a successful run down the slope in one or two trials? Remember, when he’s had his first successful run, he’s going to stop.
Hint: You may want to draw a probability tree to help visualize the problem.
P(X = 1) = P(success in the first trial) = 0.2
P(X = 2) = P(success in the second trial union failure in the first trial) = 0.8 * 0.2 = 0.16
1회 혹은 2회에서 성공할 확률
P(X <= 2) = P(X = 1) + P(X = 2) = 0.2 + 0.16 = 0.36
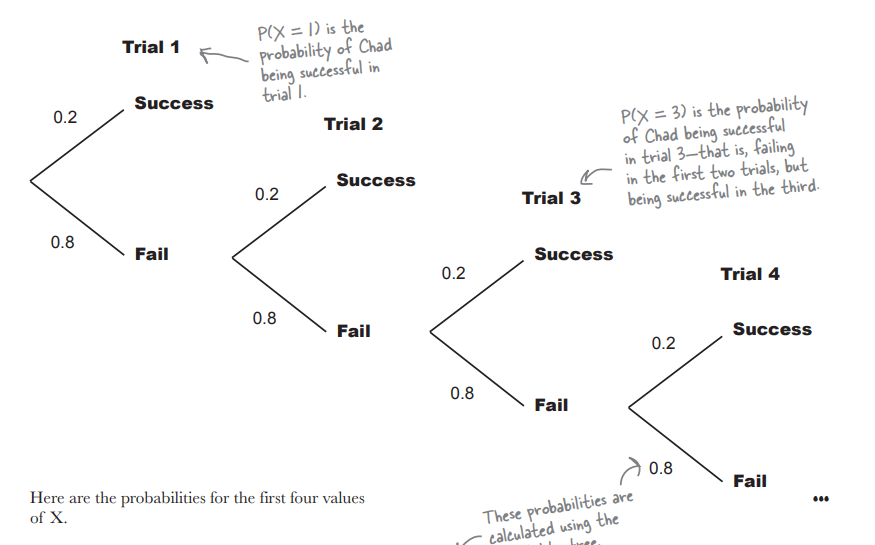
| X | P(X=x) |
| 1 | 0.2 |
| 2 | 0.8 * 0.2 = 0.16 |
| 3 | 0.8 * 0.8 * 0.2 = 0.128 |
| 4 | 0.8 * 0.8 * 0.8 * 0.2 = 0.1024 |
| . . . | . . . . . |
| X | P(X=x) | Power of 0.8 | Power of 0.2 |
| 1 | 0.80 * 0.2 | 0 | 1 |
| 2 | 0.81 * 0.2 | 1 | 1 |
| 3 | 0.82 * 0.2 | 2 | 1 |
| 4 | 0.83 * 0.2 | 3 | 1 |
| 5 | 0.84 * 0.2 | 4 | 1 |
| r | . . . . . | r - 1 | 1 |
$P(X = r) = 0.8^{r-1} × 0.2$
$P(X = r) = q^{r-1} × p $
This formula is called the geometric distribution.
- You run a series of independent trials. * (각 시행이 독립적임 = 이번 시행이 이전 시행과 상관없이 일어남)
- There can be either a success or failure for each trial, and the probability of success is the same for each trial. (성공/실패만 일어나는 상황에서, 성공하는 확률은 p로 실행햇수동안 일정)
- The main thing you’re interested in is how many trials are needed in order to get the first successful outcome. (성공하면 중단하고 성공할 때까지의 확률을 분포로 봄)
$ P(X=r) = {p \cdot q^{r-1}} $
$ P(X=r) = {p \cdot (1-p)^{r-1}} $
p = 0.20 n = 29 ## geometric . . . . ## note that it starts with 0 rather than 1 ## since the function uses p * q^(r), ## rather than p * q^(r-1) dgeom(x = 0:n, prob = p) hist(dgeom(x = 0:n, prob = p))
> p = 0.20 > n = 29 > # exact > dgeom(0:n, prob = p) [1] 0.2000000000 0.1600000000 0.1280000000 0.1024000000 0.0819200000 0.0655360000 0.0524288000 [8] 0.0419430400 0.0335544320 0.0268435456 0.0214748365 0.0171798692 0.0137438953 0.0109951163 [15] 0.0087960930 0.0070368744 0.0056294995 0.0045035996 0.0036028797 0.0028823038 0.0023058430 [22] 0.0018446744 0.0014757395 0.0011805916 0.0009444733 0.0007555786 0.0006044629 0.0004835703 [29] 0.0003868563 0.0003094850 > > hist(dgeom(x = 0:n, prob = p))
r번 시도한 이후, 그 이후 어디서든지 간에 성공을 얻을 확률
$$ P(X > r) = q^{r} $$
예, 20번 시도 후에 어디선가 성공할 확률은?
Solution.
- 21번째 성공 + 22번째 + 23번째 + . . . .
- 위는 구할 수 없음
- 따라서
- 전체 확률이 1이고 20번째까지 성공한 확률을 1에서 빼면 원하는 확률이 됨
- 1 - (1번째 성공 + 2번째 성공 + . . . + 20번째 성공)
- 그런데 이것은
- 20번까지는 실패하는 확률 = $q^{r} $ 과 같다
p <- .2 q <- 1-p n <- 19 s <- dgeom(x = 0:n, prob = p) # 20번째까지 성공할 확률을 모두 더한 확률 sum(s) # 따라서 아래는 20번 이후 어디서든지 간에서 성공할 확률 1-sum(s) ## 혹은 (교재가 이야기하는) 20번까지 실패하는 확률 q^20
> p <- .2 > q <- 1-p > n <- 19 > s <- dgeom(x = 0:n, prob = p) > # 20번째까지 성공할 확률 > sum(s) [1] 0.9884708 > # 따라서 아래는 20번 이후 어디서든지 간에서 성공할 확률 > 1-sum(s) [1] 0.01152922 > ## 혹은 (교재가 이야기하는) 20번까지 실패하는 확률 > q^20 [1] 0.01152922 >
그렇다면
r 번 이전에 성공이 있을 확률은? = r 번까지의 실패할 확률의 보수
$$ P(X \le r) = 1 - q^{r} $$
혹은 1번째 성공 + 2번째 성공 + . . . + r 번째 성공으로 구해도 된다
# r = 20 이라고 하면 p <- .2 q <- 1-p n <- 19 s <- dgeom(x = 0:n, prob = p) sum(s)
Note that
$$P(X > r) + P(X \le r) = 1 $$
Expected value
X가 성공할 확률 p를 가진 Geometric distribution을 따른다 :: $X \sim \text{Geo}(p)$
Reminding . . . Expected value in discrete probability
$E(X) = \sum x*P(X=x)$
| textbook | x | P(X = x) | xP(X = x) | xP(X ≤ x): $E(X) = \sum (x*P(X=x))$ |
| r code | trial | px ← q^(trial-1)*p | npx ← trial*(q^(trial-1))*p | plex ← cumsum(trial*(q^(trial-1))*p) |
px | npx ← trial*px | plex ← cumsum(npx) |
||
| x번째 (trial번째) 성공할 확률 | x번째의 기대치 (주사위 경우처럼) | 그 x번째까지 성공할 확률에 대한 기대값 |
- 우리가 작업하고 있는 채드의 슬로프 타기 예가 얼른 이해가 안된다면 아래 workout의 예를 들어 본다.
| x | p(x) px | npx.0 | npx = weighted probability at a given spot | plex.0 | plex | |
|---|---|---|---|---|---|---|
| 0 | 0.1 | 0 * 0.1 | 0.00 | 0.00 | 0.00 | |
| 1 | 0.15 | 1 * 0.15 | 0.15 | 0.00 + 0.15 | 0.15 | |
| 2 | 0.4 | 2 * 0.4 | 0.80 | 0.00 + 0.15 + 0.80 | 0.95 | |
| 3 | 0.25 | 3 * 0.25 | 0.75 | 0.00 + 0.15 + 0.80 + 0.75 | 1.7 | |
| 4 | 0.1 | 4 * 0.1 | 0.40 | 0.00 + 0.15 + 0.80 + 0.75 + 0.40 | 2.1 | = this is E(x) |
- x 일주일에 내가 갈 운동횟수 (workout frequency, 0 to 4)
- px 각 횟수에 대한 probability
- npx weighted probability
- plex cumulative sum of npx (to find out the below last one)
- sum of npx = 2.1 = mean of all = expected value of x = E(x)
p <- .2 q <- 1-p trial <- c(1:8) px <- q^(trial-1)*p px ## npx <- trial*(q^(trial-1))*p ## 위는 아래와 같음 npx <- trial*px npx ## plex <- cumsum(trial*(q^(trial-1))*p) ## 위는 아래와 같음 plex <- cumsum(npx) plex sumgeod <- data.frame(trial,px,npx,plex) round(sumgeod,3)
> p <- .2 > q <- 1-p > trial <- c(1,2,3,4,5,6,7,8) > px <- q^(trial-1)*p > px [1] 0.20000000 0.16000000 0.12800000 0.10240000 0.08192000 0.06553600 0.05242880 0.04194304 > npx <- trial*(q^(trial-1))*p > npx [1] 0.2000000 0.3200000 0.3840000 0.4096000 0.4096000 0.3932160 0.3670016 0.3355443 > plex <- cumsum(trial*(q^(trial-1))*p) > plex [1] 0.200000 0.520000 0.904000 1.313600 1.723200 2.116416 2.483418 2.818962 > sumgeod <- data.frame(trial,px,npx,plex) > round(sumgeod,3) trial px npx plex 1 1 0.200 0.200 0.200 2 2 0.160 0.320 0.520 3 3 0.128 0.384 0.904 4 4 0.102 0.410 1.314 5 5 0.082 0.410 1.723 6 6 0.066 0.393 2.116 7 7 0.052 0.367 2.483 8 8 0.042 0.336 2.819 >
- 아래의 예는 위의 workout 예처럼 횟수가 0-4로 정해져 있지 않고 계속 진행됨 (0-무한대)
- 하지만 여기서는 100 까지로 한정 (1:100)
- 각 지점에서의 probability = geometric probability = q^(trial-1)*p = px
- 각 지점에서의 weighted prob = trial * px = npx
- 각 단계에서의 기대값을 구하기 위한 누적합계 cumsum(npx) = plex
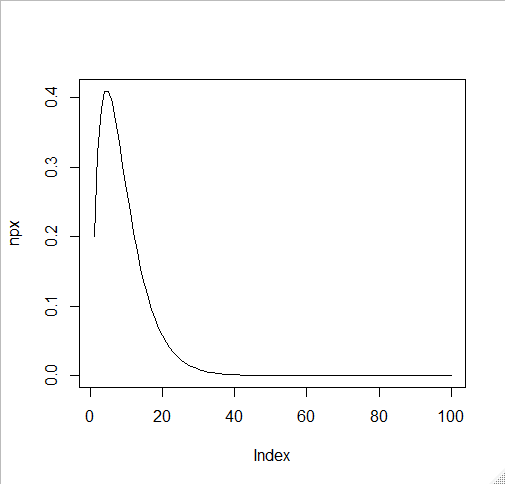
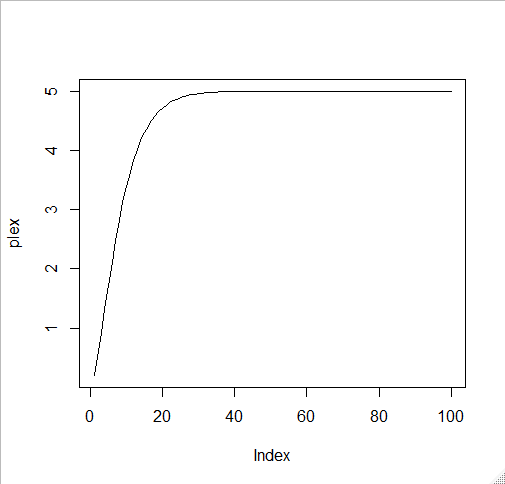
- 아래 그림에서 plex는 각 단계의 probability density를 더해온 값을 말한다.
- 그림이 암시하는 것처럼 오른 쪽으로 한 없이 가면서 생기는 그래프의 용적은 기대값이 된다.
p <- .2 q <- 1-p trial <- c(1:100) px <- q^(trial-1)*p px npx <- trial*px npx ## plex <- cumsum(trial*(q^(trial-1))*p) ## 위는 아래와 같음 plex <- cumsum(npx) plex sumgeod <- data.frame(trial,px,npx,plex) sumgeod plot(npx, type="l") plot(plex, type="l")
>
> p <- .2
> q <- 1-p
> trial <- c(1:100)
> px <- q^(trial-1)*p
> px
[1] 2.000000e-01 1.600000e-01 1.280000e-01 1.024000e-01
[5] 8.192000e-02 6.553600e-02 5.242880e-02 4.194304e-02
[9] 3.355443e-02 2.684355e-02 2.147484e-02 1.717987e-02
[13] 1.374390e-02 1.099512e-02 8.796093e-03 7.036874e-03
[17] 5.629500e-03 4.503600e-03 3.602880e-03 2.882304e-03
[21] 2.305843e-03 1.844674e-03 1.475740e-03 1.180592e-03
[25] 9.444733e-04 7.555786e-04 6.044629e-04 4.835703e-04
[29] 3.868563e-04 3.094850e-04 2.475880e-04 1.980704e-04
[33] 1.584563e-04 1.267651e-04 1.014120e-04 8.112964e-05
[37] 6.490371e-05 5.192297e-05 4.153837e-05 3.323070e-05
[41] 2.658456e-05 2.126765e-05 1.701412e-05 1.361129e-05
[45] 1.088904e-05 8.711229e-06 6.968983e-06 5.575186e-06
[49] 4.460149e-06 3.568119e-06 2.854495e-06 2.283596e-06
[53] 1.826877e-06 1.461502e-06 1.169201e-06 9.353610e-07
[57] 7.482888e-07 5.986311e-07 4.789049e-07 3.831239e-07
[61] 3.064991e-07 2.451993e-07 1.961594e-07 1.569275e-07
[65] 1.255420e-07 1.004336e-07 8.034690e-08 6.427752e-08
[69] 5.142202e-08 4.113761e-08 3.291009e-08 2.632807e-08
[73] 2.106246e-08 1.684997e-08 1.347997e-08 1.078398e-08
[77] 8.627183e-09 6.901746e-09 5.521397e-09 4.417118e-09
[81] 3.533694e-09 2.826955e-09 2.261564e-09 1.809251e-09
[85] 1.447401e-09 1.157921e-09 9.263367e-10 7.410694e-10
[89] 5.928555e-10 4.742844e-10 3.794275e-10 3.035420e-10
[93] 2.428336e-10 1.942669e-10 1.554135e-10 1.243308e-10
[97] 9.946465e-11 7.957172e-11 6.365737e-11 5.092590e-11
> npx <- trial*px
> npx
[1] 2.000000e-01 3.200000e-01 3.840000e-01 4.096000e-01
[5] 4.096000e-01 3.932160e-01 3.670016e-01 3.355443e-01
[9] 3.019899e-01 2.684355e-01 2.362232e-01 2.061584e-01
[13] 1.786706e-01 1.539316e-01 1.319414e-01 1.125900e-01
[17] 9.570149e-02 8.106479e-02 6.845471e-02 5.764608e-02
[21] 4.842270e-02 4.058284e-02 3.394201e-02 2.833420e-02
[25] 2.361183e-02 1.964504e-02 1.632050e-02 1.353997e-02
[29] 1.121883e-02 9.284550e-03 7.675228e-03 6.338253e-03
[33] 5.229059e-03 4.310012e-03 3.549422e-03 2.920667e-03
[37] 2.401437e-03 1.973073e-03 1.619997e-03 1.329228e-03
[41] 1.089967e-03 8.932412e-04 7.316071e-04 5.988970e-04
[45] 4.900066e-04 4.007165e-04 3.275422e-04 2.676089e-04
[49] 2.185473e-04 1.784060e-04 1.455793e-04 1.187470e-04
[53] 9.682448e-05 7.892109e-05 6.430607e-05 5.238022e-05
[57] 4.265246e-05 3.472060e-05 2.825539e-05 2.298743e-05
[61] 1.869645e-05 1.520236e-05 1.235804e-05 1.004336e-05
[65] 8.160232e-06 6.628619e-06 5.383242e-06 4.370871e-06
[69] 3.548119e-06 2.879633e-06 2.336616e-06 1.895621e-06
[73] 1.537559e-06 1.246898e-06 1.010998e-06 8.195824e-07
[77] 6.642931e-07 5.383362e-07 4.361904e-07 3.533694e-07
[81] 2.862292e-07 2.318103e-07 1.877098e-07 1.519771e-07
[85] 1.230291e-07 9.958120e-08 8.059129e-08 6.521410e-08
[89] 5.276414e-08 4.268560e-08 3.452790e-08 2.792587e-08
[93] 2.258353e-08 1.826109e-08 1.476428e-08 1.193576e-08
[97] 9.648071e-09 7.798028e-09 6.302080e-09 5.092590e-09
> ## plex <- cumsum(trial*(q^(trial-1))*p)
> ## 위는 아래와 같음
> plex <- cumsum(npx)
> plex
[1] 0.200000 0.520000 0.904000 1.313600 1.723200 2.116416 2.483418
[8] 2.818962 3.120952 3.389387 3.625610 3.831769 4.010440 4.164371
[15] 4.296313 4.408903 4.504604 4.585669 4.654124 4.711770 4.760192
[22] 4.800775 4.834717 4.863051 4.886663 4.906308 4.922629 4.936169
[29] 4.947388 4.956672 4.964347 4.970686 4.975915 4.980225 4.983774
[36] 4.986695 4.989096 4.991069 4.992689 4.994018 4.995108 4.996002
[43] 4.996733 4.997332 4.997822 4.998223 4.998550 4.998818 4.999037
[50] 4.999215 4.999361 4.999479 4.999576 4.999655 4.999719 4.999772
[57] 4.999814 4.999849 4.999877 4.999900 4.999919 4.999934 4.999947
[64] 4.999957 4.999965 4.999971 4.999977 4.999981 4.999985 4.999988
[71] 4.999990 4.999992 4.999993 4.999995 4.999996 4.999997 4.999997
[78] 4.999998 4.999998 4.999998 4.999999 4.999999 4.999999 4.999999
[85] 4.999999 5.000000 5.000000 5.000000 5.000000 5.000000 5.000000
[92] 5.000000 5.000000 5.000000 5.000000 5.000000 5.000000 5.000000
[99] 5.000000 5.000000
> sumgeod <- data.frame(trial,px,npx,plex)
> sumgeod
trial px npx plex
1 1 2.000000e-01 2.000000e-01 0.200000
2 2 1.600000e-01 3.200000e-01 0.520000
3 3 1.280000e-01 3.840000e-01 0.904000
4 4 1.024000e-01 4.096000e-01 1.313600
5 5 8.192000e-02 4.096000e-01 1.723200
6 6 6.553600e-02 3.932160e-01 2.116416
7 7 5.242880e-02 3.670016e-01 2.483418
8 8 4.194304e-02 3.355443e-01 2.818962
9 9 3.355443e-02 3.019899e-01 3.120952
10 10 2.684355e-02 2.684355e-01 3.389387
11 11 2.147484e-02 2.362232e-01 3.625610
12 12 1.717987e-02 2.061584e-01 3.831769
13 13 1.374390e-02 1.786706e-01 4.010440
14 14 1.099512e-02 1.539316e-01 4.164371
15 15 8.796093e-03 1.319414e-01 4.296313
16 16 7.036874e-03 1.125900e-01 4.408903
17 17 5.629500e-03 9.570149e-02 4.504604
18 18 4.503600e-03 8.106479e-02 4.585669
19 19 3.602880e-03 6.845471e-02 4.654124
20 20 2.882304e-03 5.764608e-02 4.711770
21 21 2.305843e-03 4.842270e-02 4.760192
22 22 1.844674e-03 4.058284e-02 4.800775
23 23 1.475740e-03 3.394201e-02 4.834717
24 24 1.180592e-03 2.833420e-02 4.863051
25 25 9.444733e-04 2.361183e-02 4.886663
26 26 7.555786e-04 1.964504e-02 4.906308
27 27 6.044629e-04 1.632050e-02 4.922629
28 28 4.835703e-04 1.353997e-02 4.936169
29 29 3.868563e-04 1.121883e-02 4.947388
30 30 3.094850e-04 9.284550e-03 4.956672
31 31 2.475880e-04 7.675228e-03 4.964347
32 32 1.980704e-04 6.338253e-03 4.970686
33 33 1.584563e-04 5.229059e-03 4.975915
34 34 1.267651e-04 4.310012e-03 4.980225
35 35 1.014120e-04 3.549422e-03 4.983774
36 36 8.112964e-05 2.920667e-03 4.986695
37 37 6.490371e-05 2.401437e-03 4.989096
38 38 5.192297e-05 1.973073e-03 4.991069
39 39 4.153837e-05 1.619997e-03 4.992689
40 40 3.323070e-05 1.329228e-03 4.994018
41 41 2.658456e-05 1.089967e-03 4.995108
42 42 2.126765e-05 8.932412e-04 4.996002
43 43 1.701412e-05 7.316071e-04 4.996733
44 44 1.361129e-05 5.988970e-04 4.997332
45 45 1.088904e-05 4.900066e-04 4.997822
46 46 8.711229e-06 4.007165e-04 4.998223
47 47 6.968983e-06 3.275422e-04 4.998550
48 48 5.575186e-06 2.676089e-04 4.998818
49 49 4.460149e-06 2.185473e-04 4.999037
50 50 3.568119e-06 1.784060e-04 4.999215
51 51 2.854495e-06 1.455793e-04 4.999361
52 52 2.283596e-06 1.187470e-04 4.999479
53 53 1.826877e-06 9.682448e-05 4.999576
54 54 1.461502e-06 7.892109e-05 4.999655
55 55 1.169201e-06 6.430607e-05 4.999719
56 56 9.353610e-07 5.238022e-05 4.999772
57 57 7.482888e-07 4.265246e-05 4.999814
58 58 5.986311e-07 3.472060e-05 4.999849
59 59 4.789049e-07 2.825539e-05 4.999877
60 60 3.831239e-07 2.298743e-05 4.999900
61 61 3.064991e-07 1.869645e-05 4.999919
62 62 2.451993e-07 1.520236e-05 4.999934
63 63 1.961594e-07 1.235804e-05 4.999947
64 64 1.569275e-07 1.004336e-05 4.999957
65 65 1.255420e-07 8.160232e-06 4.999965
66 66 1.004336e-07 6.628619e-06 4.999971
67 67 8.034690e-08 5.383242e-06 4.999977
68 68 6.427752e-08 4.370871e-06 4.999981
69 69 5.142202e-08 3.548119e-06 4.999985
70 70 4.113761e-08 2.879633e-06 4.999988
71 71 3.291009e-08 2.336616e-06 4.999990
72 72 2.632807e-08 1.895621e-06 4.999992
73 73 2.106246e-08 1.537559e-06 4.999993
74 74 1.684997e-08 1.246898e-06 4.999995
75 75 1.347997e-08 1.010998e-06 4.999996
76 76 1.078398e-08 8.195824e-07 4.999997
77 77 8.627183e-09 6.642931e-07 4.999997
78 78 6.901746e-09 5.383362e-07 4.999998
79 79 5.521397e-09 4.361904e-07 4.999998
80 80 4.417118e-09 3.533694e-07 4.999998
81 81 3.533694e-09 2.862292e-07 4.999999
82 82 2.826955e-09 2.318103e-07 4.999999
83 83 2.261564e-09 1.877098e-07 4.999999
84 84 1.809251e-09 1.519771e-07 4.999999
85 85 1.447401e-09 1.230291e-07 4.999999
86 86 1.157921e-09 9.958120e-08 5.000000 ###########
87 87 9.263367e-10 8.059129e-08 5.000000
88 88 7.410694e-10 6.521410e-08 5.000000
89 89 5.928555e-10 5.276414e-08 5.000000
90 90 4.742844e-10 4.268560e-08 5.000000
91 91 3.794275e-10 3.452790e-08 5.000000
92 92 3.035420e-10 2.792587e-08 5.000000
93 93 2.428336e-10 2.258353e-08 5.000000
94 94 1.942669e-10 1.826109e-08 5.000000
95 95 1.554135e-10 1.476428e-08 5.000000
96 96 1.243308e-10 1.193576e-08 5.000000
97 97 9.946465e-11 9.648071e-09 5.000000
98 98 7.957172e-11 7.798028e-09 5.000000
99 99 6.365737e-11 6.302080e-09 5.000000
100 100 5.092590e-11 5.092590e-09 5.000000
> plot(npx, type="l")
> plot(plex, type="l")
- 기댓값이 86번째 부터는 더이상 늘지 않고
- 계산된 값을 보면 5로 수렴한다.
- workout 예처럼 다섯가지의 순서가 있는 것이 아니라서
- 평균을 어떻게 나오나 보기 위해서 100까지 해 봤지만
- 86번째 이후에는 평균값이 더 늘지 않는다 (5에서)
- 따라서 위의 geometric distribution에서의 기대값은 5이다.
- 그런데 이 기대값은 아래처럼 구할 수 있다.
- 위에서 $X \sim \text{Geo}(p)$ 일때, 기대값은 $E(X) = \dfrac{1}{p}$
- 아래는 그 증명이다.
Proof of mean and variance of geometric distribution
$(4)$, $(5)$에 대한 증명은 Mean and Variance of Geometric Distribution
e.g.,
The probability that another snowboarder will make it down the slope without falling over is 0.4. Your job is to play like you’re the snowboarder and work out the following probabilities for your slope success.
- The probability that you will be successful on your second attempt, while failing on your first.
- The probability that you will be successful in 4 attempts or fewer.
- The probability that you will need more than 4 attempts to be successful.
- The number of attempts you expect you’ll need to make before being successful.
- The variance of the number of attempts.
- $P(X = 2) = p * q^{2-1}$
- $P(X \le 4) = 1 - q^{4}$
- $P(X > 4) = q^{4}$
- $E(X) = \displaystyle \frac{1}{p}$
- $Var(X) = \displaystyle \frac{q}{p^{2}}$