This is an old revision of the document!
Table of Contents
Geometric Distributions
정리
기하분포, 이항분포, 포아송분포
\begin{align*}
\text{Geometric Distribution: } \;\;\; \text{X} & \thicksim Geo(p) \\
p(X = k) & = q^{k-1} \cdot p \\
E\left[ X \right] & = \frac{1}{p} \\
V\left[ X \right] & = \frac{q}{p^2} \\
\\
\end{align*}
Geometric Distributions
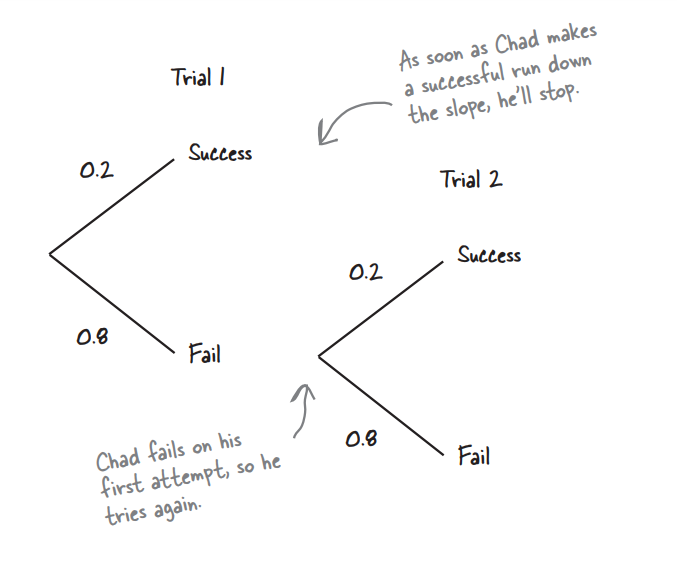
The probability of Chad making a clear run down the slope is 0.2, and he's going to keep on trying until he succeeds. After he’s made his first successful run down the slopes, he’s going to stop snowboarding, and head back to the lodge triumphantly
It’s time to exercise your probability skills. The probability of Chad making a successful run down the slopes is 0.2 for any given trial (assume trials are independent). What’s the probability he’ll need two trials? What’s the probability he’ll make a successful run down the slope in one or two trials? Remember, when he’s had his first successful run, he’s going to stop.
Hint: You may want to draw a probability tree to help visualize the problem.
P(X = 1) = P(success in the first trial) = 0.2
P(X = 2) = P(success in the second trial union failure in the first trial) = 0.8 * 0.2 = 0.16
1회 혹은 2회에서 성공할 확률
P(X <= 2) = P(X = 1) + P(X = 2) = 0.2 + 0.16 = 0.36
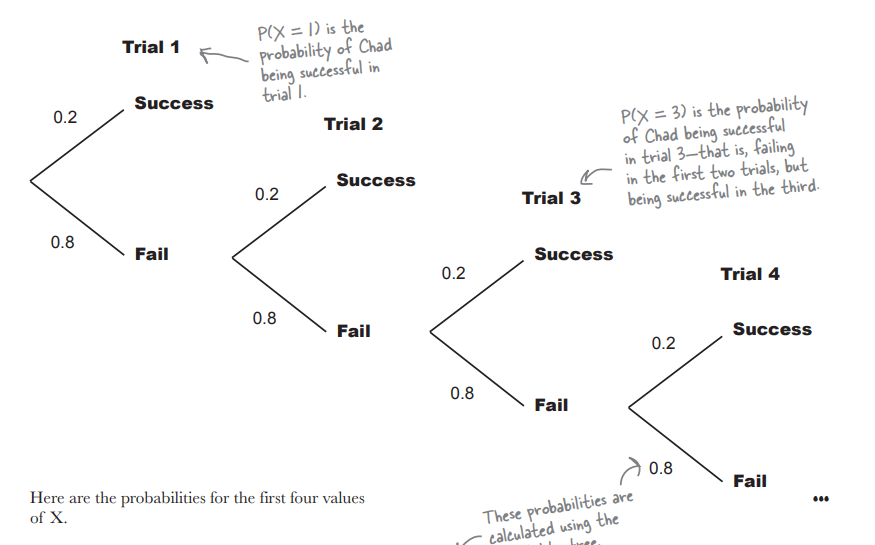
| X | P(X=x) |
| 1 | 0.2 |
| 2 | 0.8 * 0.2 = 0.16 |
| 3 | 0.8 * 0.8 * 0.2 = 0.128 |
| 4 | 0.8 * 0.8 * 0.8 * 0.2 = 0.1024 |
| . . . | . . . . . |
| X | P(X=x) | Power of 0.8 | Power of 0.2 |
| 1 | 0.80 * 0.2 | 0 | 1 |
| 2 | 0.81 * 0.2 | 1 | 1 |
| 3 | 0.82 * 0.2 | 2 | 1 |
| 4 | 0.83 * 0.2 | 3 | 1 |
| 5 | 0.84 * 0.2 | 4 | 1 |
| r | . . . . . | r - 1 | 1 |
$P(X = r) = 0.8^{r-1} × 0.2$
$P(X = r) = q^{r-1} × p $
This formula is called the geometric distribution.
- You run a series of independent trials. * (각 시행이 독립적임 = 이번 시행이 이전 시행과 상관없이 일어남)
- There can be either a success or failure for each trial, and the probability of success is the same for each trial. (성공/실패만 일어나는 상황에서, 성공하는 확률은 p로 실행햇수동안 일정)
- The main thing you’re interested in is how many trials are needed in order to get the first successful outcome. (성공하면 중단하고 성공할 때까지의 확률을 분포로 봄)
$ P(X=r) = {p \cdot q^{r-1}} $
$ P(X=r) = {p \cdot (1-p)^{r-1}} $
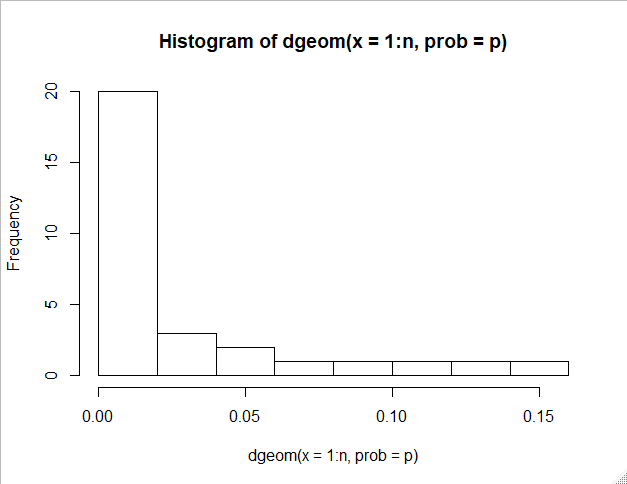
p = 0.20 n = 29 ## geometric . . . . ## note that it starts with 0 rather than 1 ## since the function uses p * q^(r), ## rather than p * q^(r-1) dgeom(x = 0:n, prob = p) hist(dgeom(x = 0:n, prob = p))
> p = 0.20 > n = 29 > # exact > dgeom(0:n, prob = p) [1] 0.2000000000 0.1600000000 0.1280000000 0.1024000000 0.0819200000 0.0655360000 0.0524288000 [8] 0.0419430400 0.0335544320 0.0268435456 0.0214748365 0.0171798692 0.0137438953 0.0109951163 [15] 0.0087960930 0.0070368744 0.0056294995 0.0045035996 0.0036028797 0.0028823038 0.0023058430 [22] 0.0018446744 0.0014757395 0.0011805916 0.0009444733 0.0007555786 0.0006044629 0.0004835703 [29] 0.0003868563 0.0003094850 > > hist(dgeom(x = 0:n, prob = p))
r번 시도한 이후, 그 이후 어디서든지 간에 성공을 얻을 확률
$$ P(X > r) = q^{r} $$
예, 20번 시도 후에 어디선가 성공할 확률은?
Solution.
- 21번째 성공 + 22번째 + 23번째 + . . . .
- 위는 구할 수 없음
- 따라서
- 전체 확률이 1이고 20번째까지 성공한 확률을 1에서 빼면 원하는 확률이 됨
- 1 - (1번째 성공 + 2번째 성공 + . . . + 20번째 성공)
- 그런데 이것은
- 20번까지는 실패하는 확률 = $q^{r} $ 과 같다
p <- .2 q <- 1-p n <- 19 s <- dgeom(x = 0:n, prob = p) # 20번째까지 성공할 확률을 모두 더한 확률 sum(s) # 따라서 아래는 20번 이후 어디서든지 간에서 성공할 확률 1-sum(s) ## 혹은 (교재가 이야기하는) 20번까지 실패하는 확률 q^20
> p <- .2 > q <- 1-p > n <- 19 > s <- dgeom(x = 0:n, prob = p) > # 20번째까지 성공할 확률 > sum(s) [1] 0.9884708 > # 따라서 아래는 20번 이후 어디서든지 간에서 성공할 확률 > 1-sum(s) [1] 0.01152922 > ## 혹은 (교재가 이야기하는) 20번까지 실패하는 확률 > q^20 [1] 0.01152922 >
그렇다면
r 번 이전에 성공이 있을 확률은? = r 번까지의 실패할 확률의 보수
$$ P(X \le r) = 1 - q^{r} $$
혹은 1번째 성공 + 2번째 성공 + . . . + r 번째 성공으로 구해도 된다
# r = 20 이라고 하면 p <- .2 q <- 1-p n <- 19 s <- dgeom(x = 0:n, prob = p) sum(s)
Note that
$$P(X > r) + P(X \le r) = 1 $$