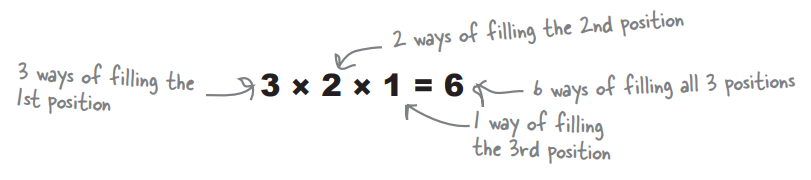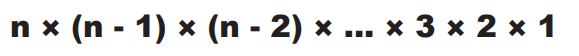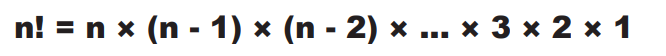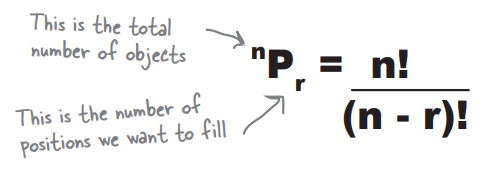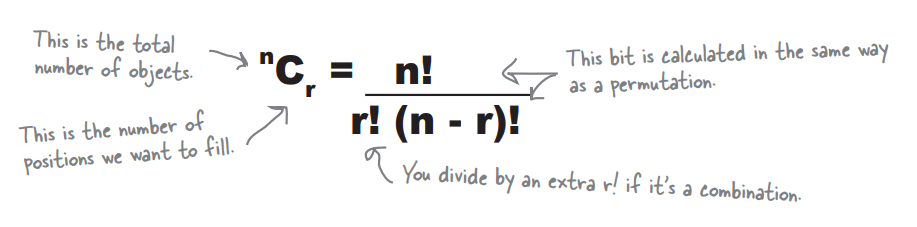Table of Contents
Permutation and Combination
순열과 조합
Permutation
세마리 말이 들어오는 순서
So what if there are n horses?
팩토리얼 (n!)
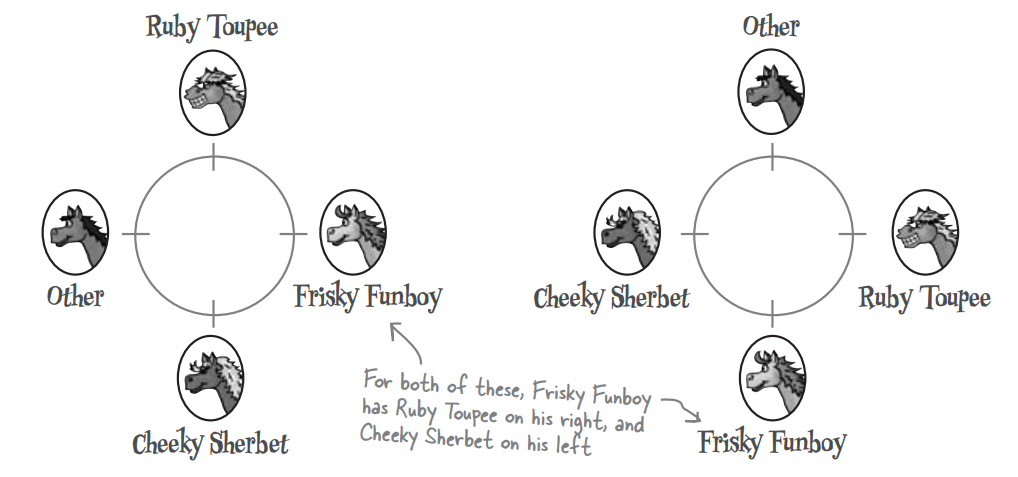
Arranging in a circle: 말한마리를 고정해 놓고 다른 말들을 배치한다고 할 때, 그 조합은?
Q: Paula wants to telephone the Statsville Health Club, but she has a very poor memory. She knows that the telephone number contains the numbers 1,2,3,4,5,6 and 7, but she can’t remember the order. What’s the probability of getting the right number at random?
A:
factorial(7)
> factorial(7) [1] 5040
Q: Paula has just been reminded that the first three numbers is some arrangement of the numbers 1, 2 and 3, and the last four numbers is some arrangement of the numbers 4, 5, 6, and 7. She can't remember the order of each set of numbers though. What's the probability of getting the right telephone number now?
factorial(3)*factorial(4)
> factorial(3)*factorial(4) [1] 144
Q: The Statsville Derby is organizing a parade for the end of the season. 10 horses are taking part, and they will parade round the race track in a circle. The exact horse order will be chosen at random, and if you guess the horse order correctly, you win a prize. What’s the probability that if you make a guess on the exact horse order, you’ll win the prize?
n <- 10 factorial(n-1)
> n <- 10 > factorial(n-1) [1] 362880 >
Arranging by individuals is different than arranging by type
by type . . . .
a, a, b ⇒
aab
aba
baa
a1, a2, b ⇒
a1, a2, b
a2, a1, b
a1, b, a2
a2, b, a1
b, a1, a2
b, a2, a1
$$ \frac {n!} {p! * q!} $$
6 horses
2 groups 3 horses per each group
factorial(6)/(factorial(3)*factorial(3))
> factorial(6)/(factorial(3)*factorial(3)) [1] 20 >
X = {a a b c c c} 라면?
n(X) = 6 이므로 총 6!
a가 둘, c가 셋으로 묶이므로
6! / (2! * 3!)
= 6*5*2 = 60
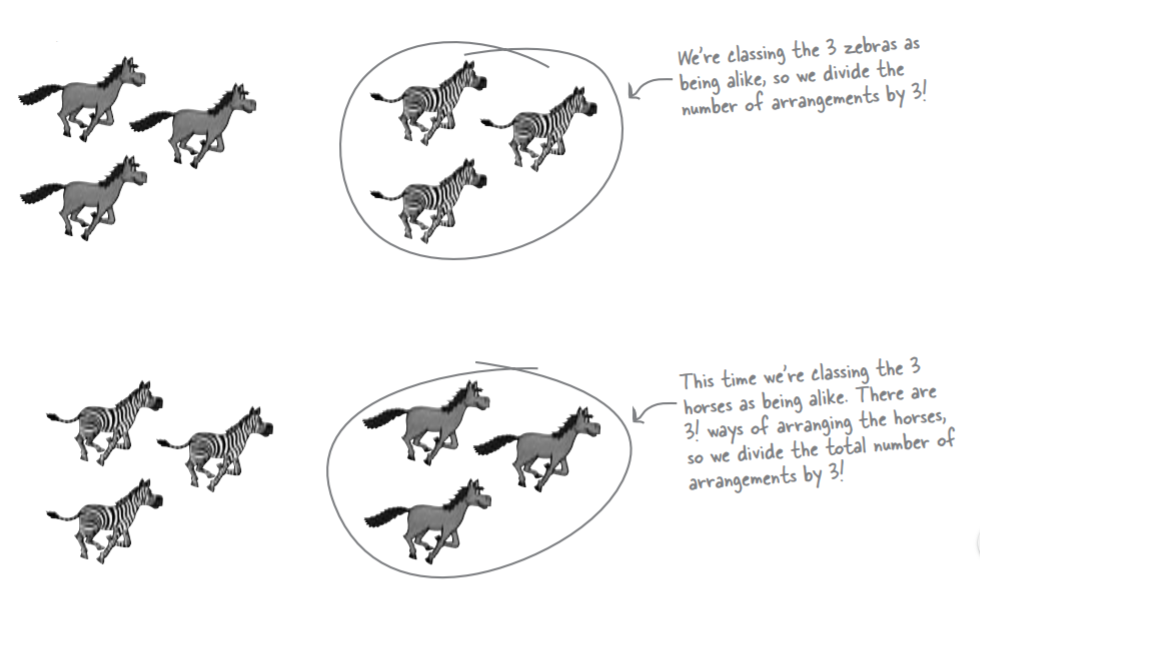
Q: The Statsville Derby have decided to experiment with their races. They've decided to hold a race between 3 horses, 2 zebras and 5 camels, where all the animals are equally likely to finish the race first.
1. How many ways are there of finishing the race if we’re interested in individual animals?
2. How many ways are there of finishing the race if we’re just interested in the species of animal in each position?
3. What's the probability that all 5 camels finish the race consecutively if each animal has an equal chance of
winning? (Assume we’re interested in the species in each position, not the individual animals themselves.)
## for Q1, there are ten animals factorial(10) ## factorial(10)/(factorial(3)*factorial(2)*factorial(5)) ## 3, 2, 1 type (5 camels as one) factorial(6)/(factorial(3)*factorial(2))
> factorial(10) [1] 3628800 > factorial(10)/(factorial(3)*factorial(2)*factorial(5)) [1] 2520 > factorial(6)/(factorial(3)*factorial(2)) [1] 60 >
Combination
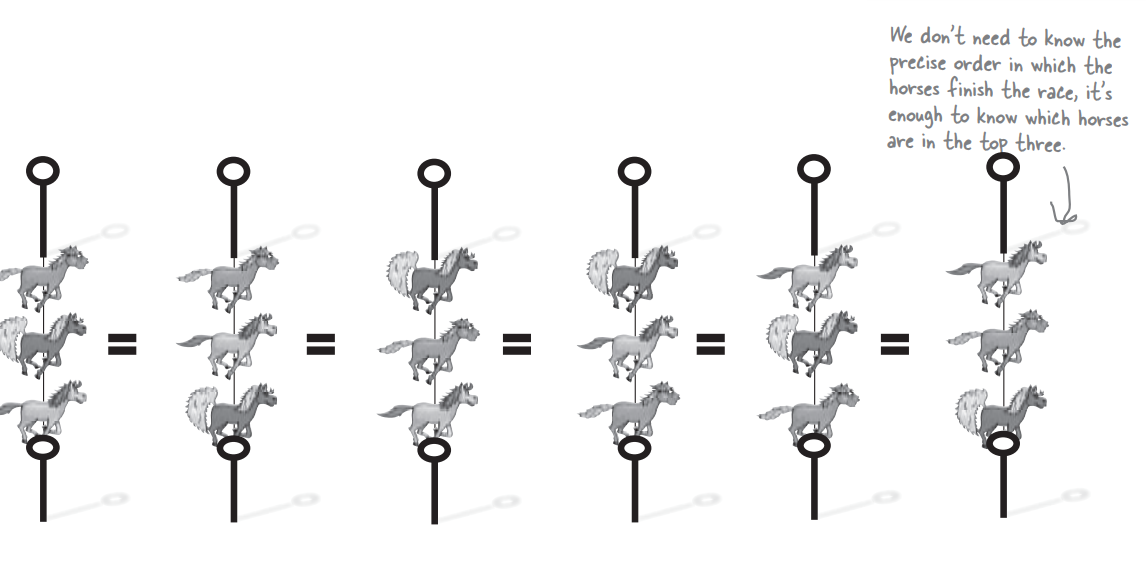
How many ways can we fill the top three positions?
20 horses
ans <- 20*19*18 ans factorial(20)/factorial(17)
> ans <- 20*19*18 > ans [1] 6840 > > factorial(20)/factorial(17) [1] 6840 > >
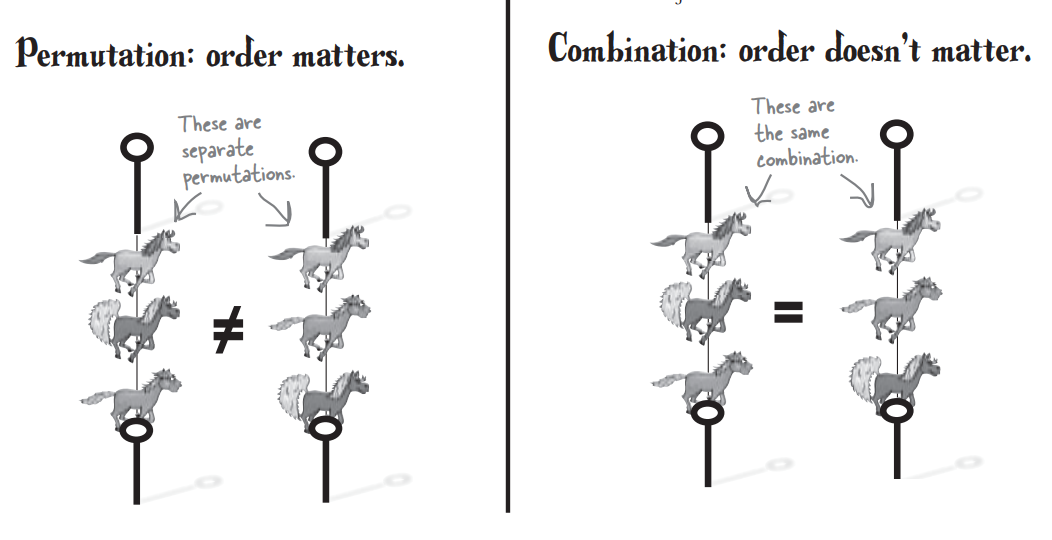
What if horse order doesn’t matter
A B C
1 head 1 sub-head
A B
B A
B C
C B
A C
C A
\begin{eqnarray*} _{3}P_{2} & = & \frac{3!}{(3-2)!} \\ & = & \frac {3!}{(3-2)!} = 6 \end{eqnarray*}
Among the two, the order doesn't matter. Then, we follow the same logic as the above
2 representatives
A B | B A
B C | C B
A C | C A
\begin{eqnarray*} \text{Answer we want} & = & \frac {_{3}P_{2}}{2!} \\ \text{We call this} & = & _{3}C_{2} \\ _{3}C_{2} & = & \frac {\frac{3!}{(3-2)!}} {\frac {2!} {1}} \\ _{3}C_{2} & = & \frac {3!}{2! * (3-2)!} = 3 \end{eqnarray*}
factorial(20)/(factorial(17)*factorial(3))
> factorial(20)/(factorial(17)*factorial(3)) [1] 1140 >
$\displaystyle {^{n} P_{r}} $
$\displaystyle ^{n} P_{r} = \displaystyle \frac {n!} {(n-r)!}$
A permutation is the number of ways in which you can choose objects from a pool, and where the order in which you choose them counts. It’s a lot more specific than a combination as you want to count the number of ways in which you fill each position.
$\displaystyle ^{n} C_{r}$
$\displaystyle ^{n} C_{r} = \displaystyle \frac {n!} {r! \cdot (n-r)!}$
A combination is the number of ways in which you can choose objects from a pool, without caring about the exact order in which you choose them. It’s a lot more general than a permutation as you don’t need to know how each position has been filled. It’s enough to know which objects have been chosen.
e.g.
The Statsville All Stars are due to play a basketball match. There are 12 players in the roster, and 5 are allowed on the court at any one time.
1. How many different arrangements are there for choosing who’s on the court at the same time?
2. The coach classes 3 of the players as expert shooters. What’s the probability that all 3 of these players will be on the court at the same time, if they’re chosen at random?
## n! / r!(n-r)! factorial(12)/(factorial(5)*factorial(12-5)) ## 3명은 같이 뛰게 되니, 2명에 대한 조합만 생각하기로 한다 ## 3명이 빠진 9명중 2명의 조합이니 ## n! / r!(n-r)! factorial(9)/(factorial(2)*factorial(9-2)) a <- factorial(12)/(factorial(5)*factorial(12-5)) b <- factorial(9)/(factorial(2)*factorial(9-2)) a b b/a
> factorial(12)/(factorial(5)*factorial(12-5)) [1] 792 > factorial(9)/(factorial(2)*factorial(9-2)) [1] 36 > a <- factorial(12)/(factorial(5)*factorial(12-5)) > b <- factorial(9)/(factorial(2)*factorial(9-2)) > a [1] 792 > b [1] 36 > b/a [1] 0.04545455 >
It’s time for you to work out some poker probabilities. See how you get on. A poker hand consists of 5 cards and there are 52 cards in a pack. How many different arrangements are there?
A royal flush is a hand that consists of a 10, Jack, Queen, King and Ace, all of the same suit. What’s the probability of getting this combination of cards? Use your answer above to help you.
Four of a kind is when you have four cards of the same denomination. Any extra card makes up the hand. What’s the probability of getting this combination?
A flush is where all 5 cards belong to the same suit. What’s the probability of getting this?
## 52장의 카드 중에서 5장 고를 조합은
factorial(52)/(factorial(5)*factorial(52-5))
all <- factorial(52)/(factorial(5)*factorial(52-5))
## royal flush = 10, 11, 12, 13, 1 각 문양
## 즉, 4가지. 따라서 전체 조합 중 4가지만 해당됨
4 / all
## four cards = 13 가지
## {1,1,1,1} {2,2,2,2} . . . . {13,13,13,13} = 13 가지
## 그리고 나머지 한장은 4장을 제외한 48장에서 조합되는 것이니
13 * (52-4)
## 위의 숫자가 four of a kinds에 해당되는 경우의 수
## 따라서 그 확률은 four cards out of five cards
(13 * (52-4)) / all
## 13 개 같은 모양 중에서 5개가 나올 조합은 13C5
## 그리고, 모양이 4 종류가 있으니 * 4를 하면
4 * (factorial(13)/(factorial(5)*factorial(13-5)))
## 그 확률은
(4 * (factorial(13)/(factorial(5)*factorial(13-5)))) / all
> ## 52장의 카드 중에서 5장 고를 조합은
> factorial(52)/(factorial(5)*factorial(52-5))
[1] 2598960
> all <- factorial(52)/(factorial(5)*factorial(52-5))
> ## royal flush = 10, 11, 12, 13, 1 각 문양
> ## 즉, 4가지. 따라서 전체 조합 중 4가지만 해당됨
> 4 / all
[1] 1.539077e-06
>
> ## four cards = 13 가지
> ## {1,1,1,1} {2,2,2,2} . . . . {13,13,13,13} = 13 가지
> ## 그리고 나머지 한장은 4장을 제외한 48장에서 조합되는 것이니
> 13 * (52-4)
[1] 624
> ## 위의 숫자가 four of a kinds에 해당되는 경우의 수
> ## 따라서 그 확률은 four cards out of five cards
> (13 * (52-4)) / all
[1] 0.000240096
>
> ## 13 개 같은 모양 중에서 5개가 나올 조합은 13C5
> ## 그리고, 모양이 4 종류가 있으니 * 4를 하면
> 4 * (factorial(13)/(factorial(5)*factorial(13-5)))
[1] 5148
> ## 그 확률은
> (4 * (factorial(13)/(factorial(5)*factorial(13-5)))) / all
[1] 0.001980792
>