$$X \sim Po(\lambda)$$

단위 시간, 단위 공간에 어떤 사건이 몇 번 발생할 것인가를 표현하는 이산 확률분포
모수(population parameter).

• 단위시간 또는 단위공간에서 평균발생횟수
• lambda (λ)로 표시
  • 한 시간 동안 은행에 다녀간 고객의 수
  • 한 시간 동안 사무실에 걸려온 전화의 수
  • 어떤 책의 한 페이지에 존재하는 오타의 수
  • 팝콘 기계가 일주일 동안 고장나는 횟수

조건

• 개별 사건이 주어진 구간에 임의로 그리고 독립적으로 발생
  • 일주일 동안
  • 1마일마다 등 시간이나 공간
• 해당 구간에서 사건이 발생하는 수의 평균값이나 비율을 알고 있음 (lambda($\lambda$))

$$ P(X=r) = e^{- \lambda} \dfrac{\lambda^{r}} {r!},\qquad k = 0, 1, 2, . . ., $$

For curiosity,
\begin{eqnarray*} \sum_{r=0}^{\infty} e^{- \lambda} \dfrac{\lambda^{r}} {r!} & = & e^{- \lambda} \sum_{r=0}^{\infty} \dfrac{\lambda^{r}} {r!} \\ & = & e^{- \lambda} \left(1 + \lambda + \dfrac{\lambda^{2}}{2!} + \dfrac{\lambda^{3}}{3!} + . . . \right) \\ & = & e^{- \lambda}e^{\lambda} \\ & = & 1 \end{eqnarray*}

왜 $e^{\lambda} = \left(1 + \lambda + \dfrac{\lambda^{2}}{2!} + \dfrac{\lambda^{3}}{3!} + . . . \right)$ 인지는 Taylor series 문서를 참조.
이것이 의미하는 것은 r이 0에서 무한대로 갈 때의 확률값의 분포를 말하므로 전체 분포가 1이 됨을 의미한다. 아래 “What does the Poisson distribution look like?” 참조

> e <- exp(1)
> e
[1] 2.718282

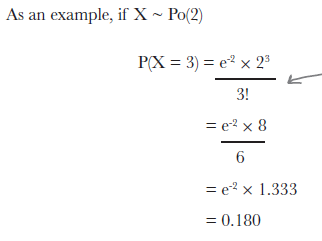
위의 그림은 lambda는 2, 즉 한달에 아주대학교 앞의 건널목 주변 찻길에서 교통사고가 날 횟수가 2회라고 할 때, X=3 이므로 3번 교통사고가 일어날 확률을 (P(X=3)) 묻는 문제이다.
\begin{eqnarray*} P(X = 3) & = & e^{-2} * \frac {2^{3}}{3!} \\ & = & 0.180 \end{eqnarray*}

\begin{eqnarray*} P(X=r) = e^{- \lambda} \dfrac{\lambda^{r}} {r!},\qquad r = 0, 1, 2, . . ., \end{eqnarray*}

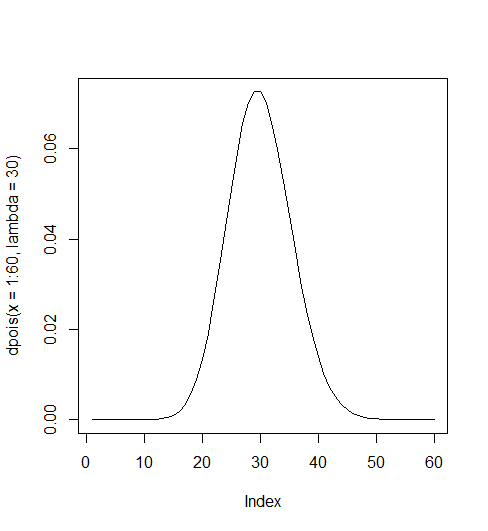
마포 신한은행 지점에 시간당 은행에 방문하는 손님의 숫자: lambda = 30

> dpois(x=1:60, lambda=30)
 [1] 2.807287e-12 4.210930e-11 4.210930e-10 3.158198e-09 1.894919e-08
 [6] 9.474593e-08 4.060540e-07 1.522702e-06 5.075675e-06 1.522702e-05
[11] 4.152825e-05 1.038206e-04 2.395861e-04 5.133987e-04 1.026797e-03
[16] 1.925245e-03 3.397491e-03 5.662486e-03 8.940767e-03 1.341115e-02
[21] 1.915879e-02 2.612562e-02 3.407689e-02 4.259611e-02 5.111534e-02
[26] 5.897924e-02 6.553248e-02 7.021338e-02 7.263453e-02 7.263453e-02
[31] 7.029148e-02 6.589826e-02 5.990751e-02 5.285957e-02 4.530820e-02
[36] 3.775683e-02 3.061365e-02 2.416867e-02 1.859128e-02 1.394346e-02
[41] 1.020253e-02 7.287524e-03 5.084319e-03 3.466581e-03 2.311054e-03
[46] 1.507209e-03 9.620485e-04 6.012803e-04 3.681308e-04 2.208785e-04
[51] 1.299285e-04 7.495876e-05 4.242949e-05 2.357194e-05 1.285742e-05
[56] 6.887904e-06 3.625212e-06 1.875110e-06 9.534457e-07 4.767229e-07
> plot(dpois(x=1:60, lambda=30), type = "l")
> 

위에서 언급한

\begin{eqnarray*} \sum_{r=0}^{\infty} e^{- \lambda} \dfrac{\lambda^{r}} {r!} & = & e^{- \lambda} \sum_{r=0}^{\infty} \dfrac{\lambda^{r}} {r!} \\ & = & e^{- \lambda} \left(1 + \lambda + \dfrac{\lambda^{2}}{2!} + \dfrac{\lambda^{3}}{3!} + . . . \right) \\ & = & e^{- \lambda}e^{\lambda} \\ & = & 1 \end{eqnarray*}

에서 1 이란 이야기는 아래 그림의 그래프가 전체가 1이 됨을 의미함. 즉 위에서는 1부터 60까지 갔지만, 1부터 무한대로 하면 완전한 분포곡선이 되는데 이것이 1이라는 뜻 (가령 dpois(x=1:1000, lambda=30)과 같은 케이스).

Figure 1. lambda=30

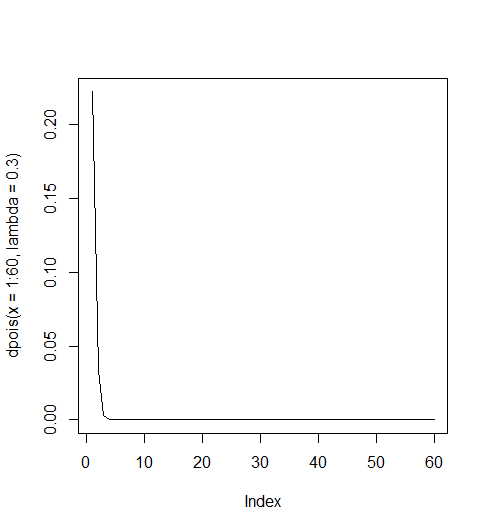
lambda가 클 수록 좌우대칭의 종형분포를 이루고 ¹⁾, 작을 수록 오른 쪽으로 편향된 (skewed to the right) 혹은 양의방향으로 편향된(positively skewed) 분포를 ²⁾ 이룬다.

> dpois(x=1:60, lambda=.3)
 [1]  2.222455e-01  3.333682e-02  3.333682e-03  2.500261e-04  1.500157e-05
 [6]  7.500784e-07  3.214622e-08  1.205483e-09  4.018277e-11  1.205483e-12
[11]  3.287682e-14  8.219204e-16  1.896739e-17  4.064441e-19  8.128883e-21
[16]  1.524166e-22  2.689704e-24  4.482840e-26  7.078168e-28  1.061725e-29
[21]  1.516750e-31  2.068296e-33  2.697777e-35  3.372222e-37  4.046666e-39
[26]  4.669230e-41  5.188033e-43  5.558607e-45  5.750283e-47  5.750283e-49
[31]  5.564790e-51  5.216991e-53  4.742719e-55  4.184752e-57  3.586930e-59
[36]  2.989108e-61  2.423601e-63  1.913370e-65  1.471823e-67  1.103867e-69
[41]  8.077076e-72  5.769340e-74  4.025121e-76  2.744401e-78  1.829600e-80
[46]  1.193218e-82  7.616283e-85  4.760177e-87  2.914394e-89  1.748636e-91
[51]  1.028610e-93  5.934286e-96  3.359030e-98 1.866128e-100 1.017888e-102
[56] 5.452971e-105 2.869985e-107 1.484475e-109 7.548177e-112 3.774089e-114
> plot(dpois(x=1:60, lambda=.3), type = "l")
> 

Figure 2. lambda = 3

일반적으로 lambda가 1보다 작으면 geometric distribution 형태의 그래프를, 1보다 크면 정규분포 형태의 모양을 갖는다.