Q. 하나의 사면체를 두 번 연속해서 던진다고 하자. 첫 번째 번호와 두 번째 번호가 같을 확률은 무엇인가? 사면체는 주사위와 같지만 1, 2, 3, 4가 아웃풋으로 나올 수 있는 물체를 의미한다.
Q. 아래의 벤다이어그램에 해당하는 부분에 표시를 하시오
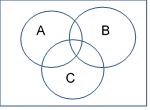
(A ∩ B ∩ ~C ) ∪ (~A ∩ B)
Q. A회사의 직원이 받는 이메일메시지의 30%는 스팸이라고 한다. A회사는 스팸버스터라는 프로그램을 이용하여 스팸메일 들이 인박스에 가기 전에 걸러내고 있다. 이 스팸버스터 프로그램은 스팸인 메일을 스팸으로 걸러낼 확률이 0.99%라고 한다. 그리고 스팸이 아닌 메일메시지를 스팸으로 오인할 확률은 5%라고 한다. 만약에 한 메일메시지가 스팸으로 표시되었는데 이 메일메시지가 스팸메일이 아닐 확률은 얼마인가?
0.3--spam -- 0.99 detect
-- 0.01 not.detect (false negative)
0.7--not.spam -- 0.05 detect (false positive)
-- 0.95 not.detect
a <- 0.3 * 0.99
b <- 0.7 * 0.05
answer = b/a+b
Q. 아래 질문에 답하시오.
- A 회사가 컴퓨터판매의 40퍼센트를 차지하지만 배달은 5퍼센트가 늦는다
- B회사는 30퍼센트를 차지하고 3퍼센트가 늦는다
- C는 30퍼센트를 차지하고 2.5퍼센트가 늦는다.
- 컴퓨터를 주문했더니 늦게 왔다. 이 컴퓨터가 A회사의 것일 확률은?
Q. 포커카드 게임에서 스트레이트플러쉬를 받을 확률은 얼마나 되는가? straight flush는 받은 다섯 장의 카드가 연속숫자를 이루면서 모두 모양이 같은 경우를 말한다.
A. P(straight flush) = ?
- 우선 스트레이트를 보면
- straight = {a, b, c, x, y} alphabet = 숫자라고 할 수 있는데
- {1,2,3,4,5}, {2,3,4,5,6}, . . . 와 같이 적어볼 수 있습니다. 여기서 가장 높은 숫자만 짚어서 보면
- 5로 끝나는 세트
- 6으로 끝나는 세트
- 7로 끝나는 세트
- . . .
- j로 끝나는 세트
- q로 끝나는 세트
- k로 끝나는 세트
- a로 끝나는 세트 가짓수가 있습니다.
- 이를 모두 세보면 10가지입니다. 그런데
- 각 번호 set마다 모양이 같은 것이 4 set가 있으므로
- (스페이드, 하트, 클로버, 다이아몬드)
- 10 * 4 = 40 이 스트레이트플러시의 경우의 숫자입니다.
Q. successful 이라는 단어의 알파벳을 이용하여 나열할 수 있는 모든 경우의 수를 구하시오.
- 10개의 알파벳이 이용되었으므로
- 10! 이라고 할 수 있지만
- s가 3번 중복될수있고,
- u가 2번
- c가 2번 중복이 있으므로
- 10! 을 (3!*2!*2!)로 나눠준다.
- R에서
factorial(10)/(factorial(3)*factorial(2)*factorial(2)) [1] 151200- 혹은
- 총 10개의 자리에 s 3개를 순서 관계없이 배치하고,
- 나머지에 (7개 자리에) 2개
- 나머지에 2개
- 3개 자리에 하나
- 2개 자리에 하나
- 하나에 하나 배치한다는 식으로 생각해도 된다.
choose(10,3)*choose(7,2)*choose(5,2)*choose(3,1)*choose(2,1)*choose(1,1)[1] 151200
Q. 두가지 질병 FLU와 COVID가 동시에 유행한다. 질병에 걸리는 90% 의 사람이 FLU에 걸린 사람이고 10%가 COVID에 걸린다. COVID에걸린 사람들의 95%가 호흡기곤란과 폐에 대한 통증이 동반되고, FLU의 경우에는 8%만이 이 증상을 동반한다. 만약에 A라는사람이 호흡기곤란과 고통의 증상이 동시에 나타난다면, 이 사람이 FLU에 걸렸을 확률은 무엇인가?
0.1 -- COVID(C) -- 0.95 호흡기곤란+폐통증(A)
-- 0.05 무증상혹은다른증상(B)
0.9 -- FLU(F) -- 0.08 호흡기곤란+폐통증(A)
-- 0.92 무증상혹은다른증상(B)
P(A) = (0.1 * 0.95) + (0.9 * 0.08)
P(F|A) = (0.9 * 0.08) / ((0.1 * 0.95) + (0.9 * 0.08))
Q. M&M 초콜릿은 1996년 이전에는 Brown, Yellow, Red 색이 각각 0.3, 0.4, 0.3 씩 들어 있었다. 1996년 이후 Blue 가 추가되어, Blue, Brown, Yellow, Red 비율이 각각 0.3, 0.2, 0.3, 0.2라고 한다. 두개의 M&M 봉지가 있다. 하나는 1994년도에 만들어진 것이고, 하나는 1997년에 만들어진 것이다. 강사가 두개의 봉지 중 하나에서 꺼낸 초콜릿이 Yellow였다고 할 때, 이 것이 1994년도에 만들어진 봉지에서 나올 확률을 구하시오.
0.5 1994 0.4 Y
0.6 nY
0.5 1997 0.3 Y
0.7 nY
P(Y) = 0.5 * 0.4 + 0.5 * 0.3
P(1994 & Y) = 0.5 * 0.4
답
0.5 * 0.4 / (0.5 * 0.4 + 0.5 * 0.3)
= 20 / 35
Q. 강사가 두개의 봉지 중 하나에서 꺼낸 초콜릿이 Red가 아니었다고 했을 때, 이 것이 1994년도에 만들어진 봉지에서 나올 확률을 구하시오.
0.5 1994 0.3 R
0.7 nR
0.5 1997 0.2 R
0.8 nR
P(nR) = 0.5*0.7 + 0.5*0.8
P(1994&nR) = 0.5*0.7
답 0.5*0.7/(0.5*0.7 + 0.5*0.8)
