c:ps1-1:note_on_statistical_test
Table of Contents
Types of Variables
- Independent Variable (IV, 독립변인): 영향을 주는 변인
- Dependent Variable (DV, 종속변인): 독립변인의 영향을 받는 변인
Level of (Variable) Measurement
- Level of Measurement 측정수준
- 종류 (N): 성별 (gendent, (M, F))
- 순서 (O): 달리기 등수 (1,2,3등)
- 숫자: GPA, 한달용돈, IQ, 통화량 (분), etc.
- (I)
- (R)
숫자 변인
- 평균, 분산, 표준편차 등의 성격을 가질 수 있음
- 종류변인의 경우에는 불가능
가설 (과 검증)
- 가설: (논리와 상식에 기반을 둔 이론에 근거하여) 두 변인 간의 관계를 예측한 선언문
- 차이
- 예1, 남자와 여자 간에 측은지심의 정도가 다를 것이다.
- 예2, 학년에 따라서 직업에 대한 관심도가 다를 것이다.
- 예3, VR을 이용해서 통계를 배운 학생과 일반 수업을 이용해서 통계를 배운 학생들 간에 통계점수가 다를 것이다.
- 예4, 업무내용을 Email로 전달하는 방법과 F2F로 전달하는 방법 간에는 업무내용에 대한 불확실성정도가 다를 것이다 (uncertainty)
- 연관
- 예1, 용돈의 정도와 학교생활의 만족도는 연관이 (상관관계가) 있을 것이다.
- 예2, 국어성적과 수학성적 간에는 연관이 있을 것이다.
- 예3, 고등학교 수능성적과 대학교 GPA 간에는 연관이 있을 것이다.
Variance
\begin{align} \sigma^2 = \frac {SS}{df} \end{align}
- $\sigma^2 = $ 한 집합에 속한 개인점수 예측에 대한 불확실성
- 한 집합에 속한 개인점수를 평균으로 예측했을 때의 불확실성
- 숫자변인의 경우에 한함
다시 가설
- 우리가 배운 것: 두 집합 간의 차이를 선언하는 가설
- 전체 (모집단) 평균과 내 집합 평균의 ($ \overline{X} $) 차이
- 아주대학교 학생의 IQ ($ \mu $) vs. 강사의 약을 먹은 학생의 (샘플 집합) IQ ($ \overline{X} $) 차이
- HOW?
- $\mu - \overline{X} $ 를
- $se $ 로 나누어 준 점수로 판단 (z-score를 구해서 테스트)
- remind:
- $\mu = 50; \sigma^2=100 $
- $\overline{X}_{(n=100)} = 54 $
- $se = \sqrt{\frac{\sigma^2} {n}} = \sqrt{\frac{100} {100}} = 1$
- $z = (54-50)/se = 4/1 = 4 $
- $zscore = 4$ 는 $\pm 2$ 범위 밖에 있으므로
- 평범한 샘플에서 나올 수 있는 샘플이 아니다 (영가설 부정)
- 원래가설 (연구가설) 채택
- = 아주대학교 대학생의 확률점수와 강사의 약을 먹은 학생샘플의 확률점수는 다를 것이다
- 이것은 $\frac {\text{difference}} {\text{random error}}$ 인 것
- random error = standard error
- = 연구자가 샘플을 prob sampling으로 잘 뽑아도 피할 수 없는 모집단 평균으로부터의 error
- 이 논리를 확장시키면
- 두 샘플 간의 평균을 구한 후
- 그 차이를 검증하는 것도 가능 (see t-test)
- 이 때의 se값은 아래처럼 구한다.
- 아래에서 $S_p^2$ 은 pooled variance 라고 부르며, 두 그룹을 하나로 묶었을 때의 variance를 말한다.
- $se = s_{\overline{X_a}-\overline{X_b}} = \displaystyle {\sqrt{\frac{S_p^2}{n_a} + \frac{S_p^2}{n_b}} }$
- pooled variance는 아래처럼 구한다.
- $s_p^2 = \displaystyle \frac{SS_a+SS_b}{df_a+df_b}$
- 여기서
- $se = \text{random error}$
- $\text{difference} = \overline{X_A} - \overline{X_B}$
- $\text{hypothesis test} = \displaystyle \frac {(\overline{X_A} - \overline{X_B}) } {se} = \displaystyle \frac {\text{difference}} {\text{random error}}$
see t-test example 3
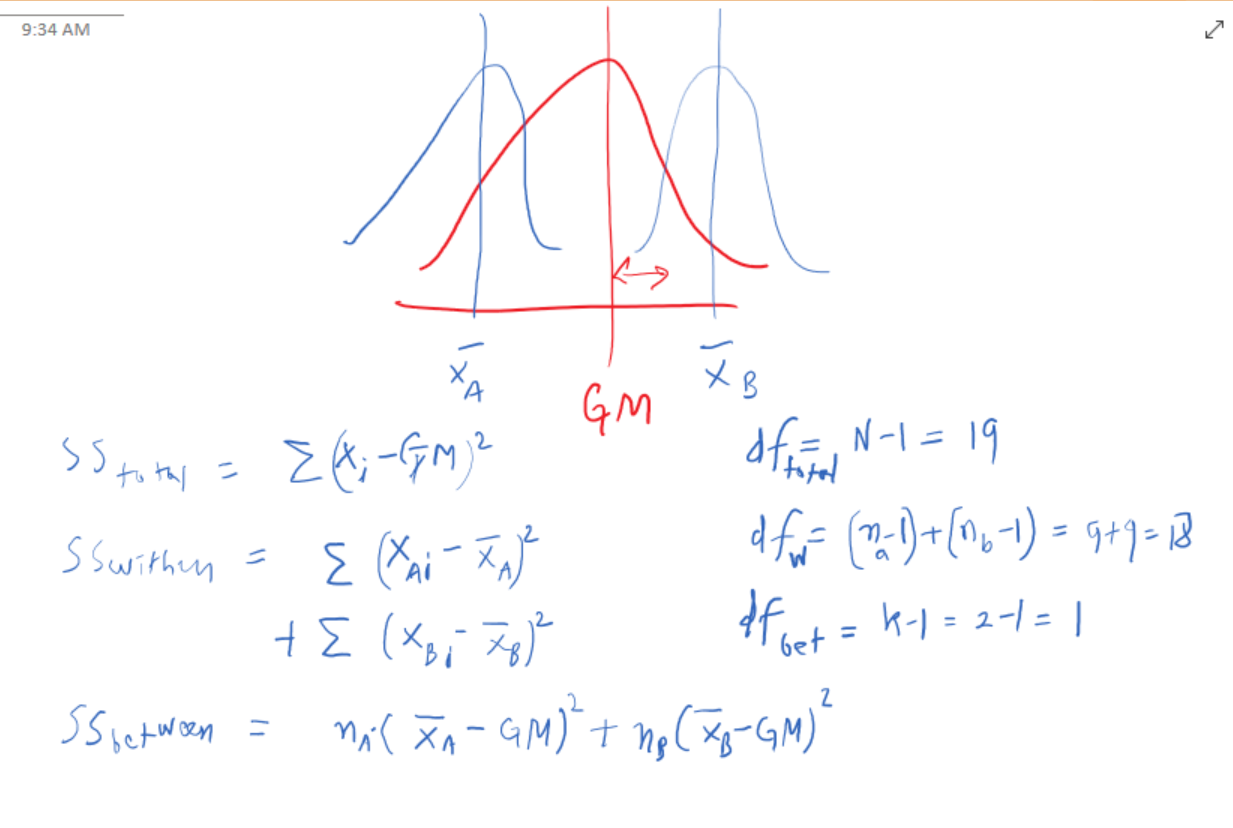
Different Way of Doing it
c/ps1-1/note_on_statistical_test.txt · Last modified: by hkimscil