Why n-1

문제.

우리는 모집단의 (population) 평균값을 알고 있다면 샘플의 분산값을 다음과 같이 구할 수 있다. 그리고, 이것을 모집단의 분산값으로 추정할 수 있다.

\begin{eqnarray*} \hat{\sigma^{2}} = \dfrac {\displaystyle\sum_{i=1}^{n}{(X_{i}-\mu)}} {n} \end{eqnarray*}

그러나, 현재 우리가 가지고 있는 것은 샘플 밖에 없다. 즉, 모집단의 평균은 알지 못하는 상태이기에 모집단 분산을 추정하는 계산에 사용할 수 없다. 따라서 샘플의 평균을 사용한다. 그런데, 샘플의 평균을 사용할 때는 분모에 N 대신에 n-1을 사용해야 한다. 왜 n-1을 사용하는것이 모집단의 분산값 추정에 도움이 되는가가 문제이다.

\begin{eqnarray*} \hat{\sigma}^{2} \neq \frac {\displaystyle\sum_{i=1}^{n}{(X_{i}-\overline{X})}} {n} \end{eqnarray*}

\begin{eqnarray*} \hat{\sigma}^{2} = \frac {\displaystyle\sum_{i=1}^{n}{(X_{i}-\overline{X})}} {n-1} \end{eqnarray*}

이 모집단의 분산값을 ($\sigma^2$) 대표함을 알아보는 것이 문제이다.

직관적 이해

분산은 $ \text{SS}/ \text{df} $ 라고 배웠다. SS = Sum of Something Square라고 설명하고, 여기서 Something 은 error (개인의 점수를 평균으로 추측했을 때 틀린 만큼의 에러값) 하였다. 이렇게 평균을 가지고 개인점수를 예측하는 것이 가장 작은 오차를 갖는 방법이라고 하였다 (개인점수 중에서 평균이 제일 많이 나오므로, 평균으로 개인점수를 예측하면 제일 들 틀린다). 따라서 어느 한 집합에서 (샘플에서) 개인점수에서 평균을 빼고 이를 제곱하여 모두 더한 값은 (평균이 아닌) 다른 값으로 구한 값보다 항상 작게 된다 (최소값을 갖는다).

이를 그림으로도 설명할 수 있다. 아래에서 녹색의 세로선은 모집단의 평균값이고, 붉은색의 세로선은 3개로 이루어진 샘플의 평균값이다. 그리고 녹색 가로선은 3개의 샘플요소와 모집단평균과의 ($\mu$) 차이값들이고, 적색가로선은 3개의 샘플요소와 샘플평균과의 ($\overline{X}$) 차이값이다. 이 차이값들을 모아서 길이를 비교한 것이 그래프의 하단이다. 적색가로선 세개의 합이 녹색가로선 세개의 합보다 작다. 이는 샘플평균을 사용했을 때와 모집단의 평균을 사용했을 때를 비교하는 것이지만 모집단 평균외에 다른 값을 썼어도 마찬가지이다.

실험적, R에서 시뮬레이션으로 이해

아래 output의 코멘트를 읽을 것

rm(list=ls())

rnorm2 <- function(n,mean,sd){ 
  mean+sd*scale(rnorm(n)) 
}

# set.seed(191)
nx <- 1000
mx <- 50
sdx <- mx * 0.1
sdx  # 5
x <- rnorm2(nx, mx, sdx)
# x <- rnorm2(1000, 50, 5) 와 동일

mean(x)
sd(x)
length(x)
hist(x)

x.span <- seq(from = mean(x)-3*sd(x), 
              to = mean(x)+3*sd(x), 
              by = .1)
x.span

residuals <- function(x, v) {
  return(x - v)
}

# sum of square residual 값을 
# 구하는 펑션
ssr <- function(x, v) { 
  residuals <- (x - v)
  return(sum(residuals^2))
}

#  mean square residual 값을 
# 구하는 펑션 (mean square 
# residual = variance)
msr <- function(x, v) {
  residuals <- (x - v)
  return((mean(residuals^2)))
}

ssrs <- c() # sum of square residuals
msrs <- c() # mean square residuals = variance
vs <- c() # the value of v in (x - v)

# x.span의 값들을 v값으로 삼아 sum(x-x.span)^2 처럼 구하면
# SS값을 구한 것이 된다. 우리가 배운 SS값은 x.span의 값으로 
# 샘플의 평균을 사용했을 때의 residual 값이다. x.span은 
# 샘플의 평균을 중심으로 여러가지 값을 사용하는 것을 가정한다.

for (i in x.span) {
  res.x <- residuals(x,i)
  msr.x <- msr(x,i)
  msrs <- append(msrs, msr.x)
  vs <- append(vs, i)
}
# 아래 plot은 SS값들이나 (두번째는) MS값들을 v값이 변화함에 
# 따라서 (x.span의 범위에 따라서 변화) 어떻게 변화하는지 
# 구한 것

plot(msrs)

# v값이 x.span에 따라서 변화하여 대입되었을 때의
# MS값들을 (msr 펑션으로 구한 mean square값)
# 모아 놓은 값이 msrs
msrs 

# 아래는 위에서 계산한 msr 값들을 저장한 msrs값들 중에서 최소값이 
# 되는 것을 찾은 것. 우리는 이것이 샘플의 평균임을 안다. 
min(msrs)
# 최소값일 때의 위치 (msrs에서 몇번째인지)
min.pos.msrs <- which(msrs == min(msrs))
min.pos.msrs
# msr 최소값이 구해졌을 때 사용된 v값
vs[min.pos.msrs]

output

> rm(list=ls())
> 
> rnorm2 <- function(n,mean,sd){ 
+     mean+sd*scale(rnorm(n)) 
+ }
> 
> # set.seed(191)
> nx <- 1000
> mx <- 50
> sdx <- mx * 0.1
> sdx  # 5
[1] 5
> x <- rnorm2(nx, mx, sdx)
> # x <- rnorm2(1000, 50, 5) 와 동일
> 
> mean(x)
[1] 50
> sd(x)
[1] 5
> length(x)
[1] 1000
> hist(x)
>

SS = sum(x-mean(x))^2 인데, mean(x)을 즉, x집합의 평균을, x 원소값을 예측하는데 (빼는데) 사용하면 SS값이 최소값이 된다고 하였다. 이것을 R에서 simulation으로 알아보기 위해서 mean(x) 대신에 다른 숫자들을 넣어보려고 한다. 이를 v라고 하면 sum(x-v)^2이라는 SS값들을 구해서 비교하려는 것이다. 대입할 숫자들은 (v) mean(x) +- 3 sd(x) 를 범위로 하고, 그 범위의 시작 숫자에서 (시작은 mean(x)-3sd(x)가 된다) 0.1씩 증가시키면서 대입하고, 각 숫자마다 (처음 숫자는 35, 다음 숫자는 35.1 . . . ) SS값을 구해서 저장하여 그것을 그래프로 그려보고 최소값이 어떤 것인지 보는 것이 진행하려는 작업이다.

단, 이 코드에서 SS대신 MS값을 (SS값을 n으로 나눈 값, 즉, variance값 혹은 Mean Square값) 구해서 보려고 하는데 이것은 같은 의미를 갖는다. 즉, 모든 SS값들에 n을 공토으로 나누어준 값을 저장하고 비교하려는 것이다.

> x.span <- seq(from = mean(x)-3*sd(x), 
+               to = mean(x)+3*sd(x), 
+               by = .1)
> x.span
  [1] 35.0 35.1 35.2 35.3 35.4 35.5 35.6 35.7 35.8
 [10] 35.9 36.0 36.1 36.2 36.3 36.4 36.5 36.6 36.7
 [19] 36.8 36.9 37.0 37.1 37.2 37.3 37.4 37.5 37.6
 [28] 37.7 37.8 37.9 38.0 38.1 38.2 38.3 38.4 38.5
 [37] 38.6 38.7 38.8 38.9 39.0 39.1 39.2 39.3 39.4
 [46] 39.5 39.6 39.7 39.8 39.9 40.0 40.1 40.2 40.3
 [55] 40.4 40.5 40.6 40.7 40.8 40.9 41.0 41.1 41.2
 [64] 41.3 41.4 41.5 41.6 41.7 41.8 41.9 42.0 42.1
 [73] 42.2 42.3 42.4 42.5 42.6 42.7 42.8 42.9 43.0
 [82] 43.1 43.2 43.3 43.4 43.5 43.6 43.7 43.8 43.9
 [91] 44.0 44.1 44.2 44.3 44.4 44.5 44.6 44.7 44.8
[100] 44.9 45.0 45.1 45.2 45.3 45.4 45.5 45.6 45.7
[109] 45.8 45.9 46.0 46.1 46.2 46.3 46.4 46.5 46.6
[118] 46.7 46.8 46.9 47.0 47.1 47.2 47.3 47.4 47.5
[127] 47.6 47.7 47.8 47.9 48.0 48.1 48.2 48.3 48.4
[136] 48.5 48.6 48.7 48.8 48.9 49.0 49.1 49.2 49.3
[145] 49.4 49.5 49.6 49.7 49.8 49.9 50.0 50.1 50.2
[154] 50.3 50.4 50.5 50.6 50.7 50.8 50.9 51.0 51.1
[163] 51.2 51.3 51.4 51.5 51.6 51.7 51.8 51.9 52.0
[172] 52.1 52.2 52.3 52.4 52.5 52.6 52.7 52.8 52.9
[181] 53.0 53.1 53.2 53.3 53.4 53.5 53.6 53.7 53.8
[190] 53.9 54.0 54.1 54.2 54.3 54.4 54.5 54.6 54.7
[199] 54.8 54.9 55.0 55.1 55.2 55.3 55.4 55.5 55.6
[208] 55.7 55.8 55.9 56.0 56.1 56.2 56.3 56.4 56.5
[217] 56.6 56.7 56.8 56.9 57.0 57.1 57.2 57.3 57.4
[226] 57.5 57.6 57.7 57.8 57.9 58.0 58.1 58.2 58.3
[235] 58.4 58.5 58.6 58.7 58.8 58.9 59.0 59.1 59.2
[244] 59.3 59.4 59.5 59.6 59.7 59.8 59.9 60.0 60.1
[253] 60.2 60.3 60.4 60.5 60.6 60.7 60.8 60.9 61.0
[262] 61.1 61.2 61.3 61.4 61.5 61.6 61.7 61.8 61.9
[271] 62.0 62.1 62.2 62.3 62.4 62.5 62.6 62.7 62.8
[280] 62.9 63.0 63.1 63.2 63.3 63.4 63.5 63.6 63.7
[289] 63.8 63.9 64.0 64.1 64.2 64.3 64.4 64.5 64.6
[298] 64.7 64.8 64.9 65.0

x-mean(x) = residual = error
sum(residual^2) = SS (sum of square)
SS/n = variance, mean square (ms, MS)

이 residual을 구하기 위해서 쓰는 mean(x)의 대체값들을 (v값들) x.span에 모아 놓은 것이다.
이 값을 출력해보았는데 35.1 에서 시작하여 65에서 끝나며, 0.1씩 증가한다.

> 
> residuals <- function(x, v) {
+     return(x - v)
+ }
> 
> # sum of square residual 값을 
> # 구하는 펑션
> ssr <- function(x, v) { 
+     residuals <- (x - v)
+     return(sum(residuals^2))
+ }
> 
> #  mean square residual 값을 
> # 구하는 펑션 (mean square 
> # residual = variance)
> msr <- function(x, v) {
+     residuals <- (x - v)
+     return((mean(residuals^2)))
+ }
>

이 후 쓸 function들. (x-v) = residual이라고 부르니까 이 residual을 모으는 function
function ssr = x 집합과 v값 (x.span의 한 숫자)를 인수를 주었을 때 구할 수 있는 Sum of Square값들 (실제로는 사용하지 않는다. 대신 msr 펑션으로 MS값을 구한다).
function msr = 의 ssr을 n으로 나누어 구한 mean square residual을 (분산) 구하는 function

> ssrs <- c() # sum of square residuals
> msrs <- c() # mean square residuals = variance
> vs <- c() # the value of v in (x - v)
> 
> # x.span의 값들을 v값으로 삼아 sum(x-x.span)^2 처럼 구하면
> # SS값을 구한 것이 된다. 우리가 배운 SS값은 x.span의 값으로 
> # 샘플의 평균을 사용했을 때의 residual 값이다. x.span은 
> # 샘플의 평균을 중심으로 여러가지 값을 사용하는 것을 가정한다.
> 
> for (i in x.span) {
+     res.x <- residuals(x,i)
+     msr.x <- msr(x,i)
+     msrs <- append(msrs, msr.x)
+     vs <- append(vs, i)
+ }
> # 아래 plot은 SS값들이나 (두번째는) MS값들을 v값이 변화함에 
> # 따라서 (x.span의 범위에 따라서 변화) 어떻게 변화하는지 
> # 구한 것
> 
> plot(vs, msrs)
>

comment

x.span의 처음값인 35.1을 넣어서 (x-v)를 구한 후
msr 펑션으로 mean square residual 값을 구한다.
그리고 이 값을 어딘가에 (msrs) 저장한 후
그 다음 value인 35.2값을 v 대신에 넣어 다시
msr값을 구하여 위의 msrs에 추가하여 저장한다.
이것을 x.span의 모든값에 걸쳐 진행하면
msrs에는 x.span의 모든 값을 대응하여 구한
msr값들이 저장된다. 이 msr값 중에서 최소값을 찾고
이 최소값을 구할 때 쓴 v값을 (x.span 중 하나의 값) 찾고자 한다.
이를 위해서 for 를 이용한 loop문을 쓴다.

> # v값이 x.span에 따라서 변화하여 대입되었을 때의
> # MS값들을 (msr 펑션으로 구한 mean square값)
> # 모아 놓은 값이 msrs
> msrs 
  [1] 249.975 246.985 244.015 241.065 238.135
  [6] 235.225 232.335 229.465 226.615 223.785
 [11] 220.975 218.185 215.415 212.665 209.935
 [16] 207.225 204.535 201.865 199.215 196.585
 [21] 193.975 191.385 188.815 186.265 183.735
 [26] 181.225 178.735 176.265 173.815 171.385
 [31] 168.975 166.585 164.215 161.865 159.535
 [36] 157.225 154.935 152.665 150.415 148.185
 [41] 145.975 143.785 141.615 139.465 137.335
 [46] 135.225 133.135 131.065 129.015 126.985
 [51] 124.975 122.985 121.015 119.065 117.135
 [56] 115.225 113.335 111.465 109.615 107.785
 [61] 105.975 104.185 102.415 100.665  98.935
 [66]  97.225  95.535  93.865  92.215  90.585
 [71]  88.975  87.385  85.815  84.265  82.735
 [76]  81.225  79.735  78.265  76.815  75.385
 [81]  73.975  72.585  71.215  69.865  68.535
 [86]  67.225  65.935  64.665  63.415  62.185
 [91]  60.975  59.785  58.615  57.465  56.335
 [96]  55.225  54.135  53.065  52.015  50.985
[101]  49.975  48.985  48.015  47.065  46.135
[106]  45.225  44.335  43.465  42.615  41.785
[111]  40.975  40.185  39.415  38.665  37.935
[116]  37.225  36.535  35.865  35.215  34.585
[121]  33.975  33.385  32.815  32.265  31.735
[126]  31.225  30.735  30.265  29.815  29.385
[131]  28.975  28.585  28.215  27.865  27.535
[136]  27.225  26.935  26.665  26.415  26.185
[141]  25.975  25.785  25.615  25.465  25.335
[146]  25.225  25.135  25.065  25.015  24.985
[151]  24.975  24.985  25.015  25.065  25.135
[156]  25.225  25.335  25.465  25.615  25.785
[161]  25.975  26.185  26.415  26.665  26.935
[166]  27.225  27.535  27.865  28.215  28.585
[171]  28.975  29.385  29.815  30.265  30.735
[176]  31.225  31.735  32.265  32.815  33.385
[181]  33.975  34.585  35.215  35.865  36.535
[186]  37.225  37.935  38.665  39.415  40.185
[191]  40.975  41.785  42.615  43.465  44.335
[196]  45.225  46.135  47.065  48.015  48.985
[201]  49.975  50.985  52.015  53.065  54.135
[206]  55.225  56.335  57.465  58.615  59.785
[211]  60.975  62.185  63.415  64.665  65.935
[216]  67.225  68.535  69.865  71.215  72.585
[221]  73.975  75.385  76.815  78.265  79.735
[226]  81.225  82.735  84.265  85.815  87.385
[231]  88.975  90.585  92.215  93.865  95.535
[236]  97.225  98.935 100.665 102.415 104.185
[241] 105.975 107.785 109.615 111.465 113.335
[246] 115.225 117.135 119.065 121.015 122.985
[251] 124.975 126.985 129.015 131.065 133.135
[256] 135.225 137.335 139.465 141.615 143.785
[261] 145.975 148.185 150.415 152.665 154.935
[266] 157.225 159.535 161.865 164.215 166.585
[271] 168.975 171.385 173.815 176.265 178.735
[276] 181.225 183.735 186.265 188.815 191.385
[281] 193.975 196.585 199.215 201.865 204.535
[286] 207.225 209.935 212.665 215.415 218.185
[291] 220.975 223.785 226.615 229.465 232.335
[296] 235.225 238.135 241.065 244.015 246.985
[301] 249.975
>

comment

msrs값에 저장된 msr값들 (mean square residual값들) 중에서
가장 작은 값을 찾아서 그 값을 구하도록 한 v값을 찾고자 한다.
msrs값을 눈으로 살펴보기에는 너무 힘드므로 . . . .

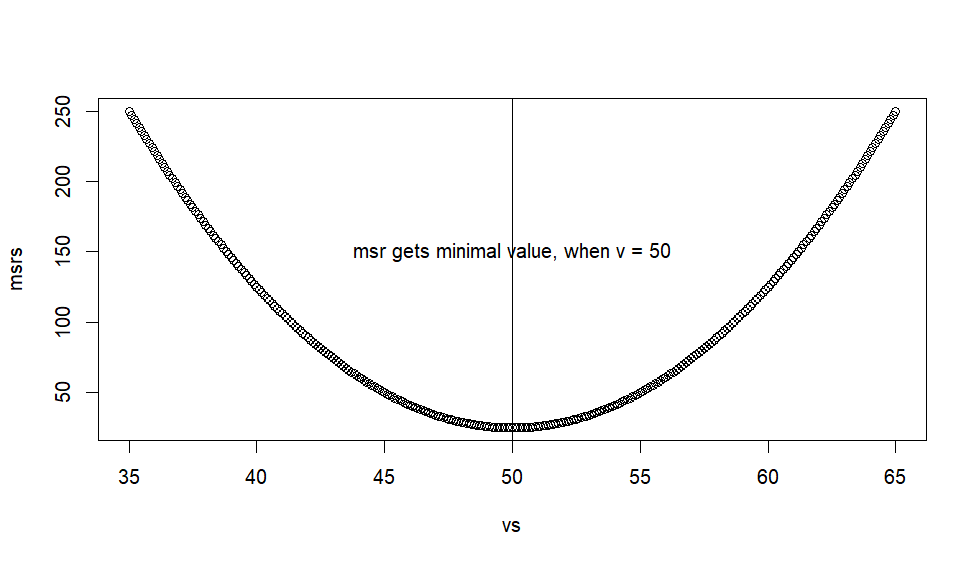
> # 아래는 위에서 계산한 msr 값들을 저장한 msrs값들 중에서 최소값이 되는 것을 찾은 
> # 것. 우리는 이것이 샘플의 평균임을 안다. 
> min(msrs)
[1] 24.975
> # 최소값일 때의 위치 (msrs에서 몇번째인지)
> min.pos.msrs <- which(msrs == min(msrs))
> min.pos.msrs
[1] 151
> # msr 최소값이 구해졌을 때 사용된 v값
> vs[min.pos.msrs]
[1] 50
> 
> plot(vs, msrs, cex=1, lwd=1, lty=3)
> abline(v=vs[min.pos.msrs])
> text(x=50, y=150, "msr gets minimal value, when v = 50" )
>
>
>
>
>
>
>

comment

msrs 의 min(msrs)값을 찾는다 24.975
이 최소값이 어느 위치에 있는지 (몇번째 자리에 있는지) 찾는다 which(msrs == min(msrs))
이 위치가 151이다
이 151번째 사용된 (최소값인 msr값 = mean(x-v)^2)을 결과한) vs값을 찾는다 (vs[151])
이 값을 출력하니 50 이고 이 값은 x의 평균값이다.
이를 plot으로 출력한 것

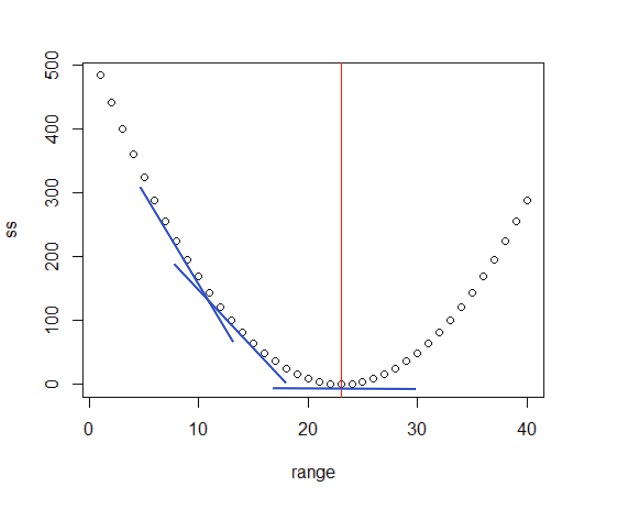
다음으로 MS값을 구하는 식인

y = sum( (x-v)^2 ) / n 값을
~~v에 대해서~~ v를 가지고 y를 미분하면 (dy/dv)
변화하는 v값마다의 기울기 값을 구할 수 있는데
이 값이 0이 되는 지점의 v값이 무엇인지를 구하면 위의 R코드에서 구한 값을 구할 수 있게 된다. 아래는 그 과정이다.
그래프에서 가장 작은 기울기값을 갖는 v 값을 구한다고 (derivatives) 가정하고 이해를 하면 수학적으로 이해할 수 있다. ¹⁾

\begin{eqnarray*} \dfrac{dy}{dv} = \dfrac{\text{d}}{\text{dv}} \dfrac{\sum{(x-v)^2}}{n} & = & \dfrac {\sum{2(x-v)*(-1)}}{n} \\ & = & \dfrac{\sum{-2(x-v)}}{n} \\ & = & -\dfrac{2}{n} \sum{(x-v)} \\ \end{eqnarray*}
위의 식이 0이 (기울기가 0이 되는 부분) 될 때의 v 값을 찾아야 하므로

\begin{eqnarray*} -\dfrac{2}{n} \sum{(x-v)} & = & 0 \\ \sum{(x-v)} & = & 0 \\ \sum{x} - n*v & = & 0 \\ n*v & = & \sum{x} \\ v & = & \dfrac {\sum{x}}{n} \\ \end{eqnarray*}

즉, 기울기가 0이 될때의 v값은 x집합의 평균값일 때이다.

R에서 msr이 최소값이 되는 v값 효율적으로 찾기

위의 미분을 이용한 방법을 써서 MS값이 최소값이 되는 순간을 R에서 구현해 볼 수 있다. 아래 아웃풋의 코멘트 부분을 읽을 것.
~~why n-1 gradient explanation~~

# the above no gradient

gradient <- function(x, v){
    residuals = x - v
    # y = (sum(x-v)^2)/n 혹은 (mean(x-v)^2) 
    # 의 식이 ms값을 구하는 식인데 
    # 이를 v에 대해서 미분하면 chain rule을 써야 한다
    # 자세한 것은 http://commres.net/wiki/estimated_standard_deviation
    # 문서 중에 미분 부분 참조
    # dy/dv = ( 2(x-v)*-1 ) / n chain rule
    # dy/dv = -2 (x-v) / n = -2 (mean(residual)) 
    dx = -2 * mean(residuals)
    # return(list("ds" = dx))
    return(dx)
} # function returns ds value

zx <- (x-mean(x))/sd(x)
# pick one random v in (x-v)
v <- rnorm(1)

# Train the model with scaled features
learning.rate = 1e-1

msrs <- c()
vs <- c()

nlen <- 75
for (epoch in 1:nlen) {
    residual <- residuals(zx, v)
    msr.x <- msr(zx, v)
    msrs <- append(msrs, msr.x)
    
    grad <- gradient(zx, v)
    step.v <- grad * learning.rate # 
    v <- v - step.v # 그 다음 v값
    vs <- append(vs, v) # v값 저장
}

tail(msrs)
tail(vs)

plot(vs, msrs, type='b')

# scaled
vs # 변화하는 v 값들의 집합 
vs.orig <- (vs*sd(x))+mean(x) 
vs.orig

# 마지막 v값이 최소값에 근접한 값
v 
v.orig <- (v*sd(x))+mean(x) 
v.orig

plot(vs.orig, msrs, type='b')

output

> # the above no gradient
> 
> gradient <- function(x, v){
+     residuals = x - v
+     # y = (sum(x-v)^2)/n 혹은 (mean(x-v)^2) 
+     # 의 식이 ms값을 구하는 식인데 
+     # 이를 v에 대해서 미분하면 chain rule을 써야 한다
+     # 자세한 것은 http://commres.net/wiki/estimated_standard_deviation
+     # 문서 중에 미분 부분 참조
+     # dy/dv = ( 2(x-v)*-1 ) / n chain rule
+     # dy/dv = -2 (x-v) / n = -2 (mean(residual)) 
+     dx = -2 * mean(residuals)
+     # return(list("ds" = dx))
+     return(dx)
+ } # function returns ds value
> 




















>

comment
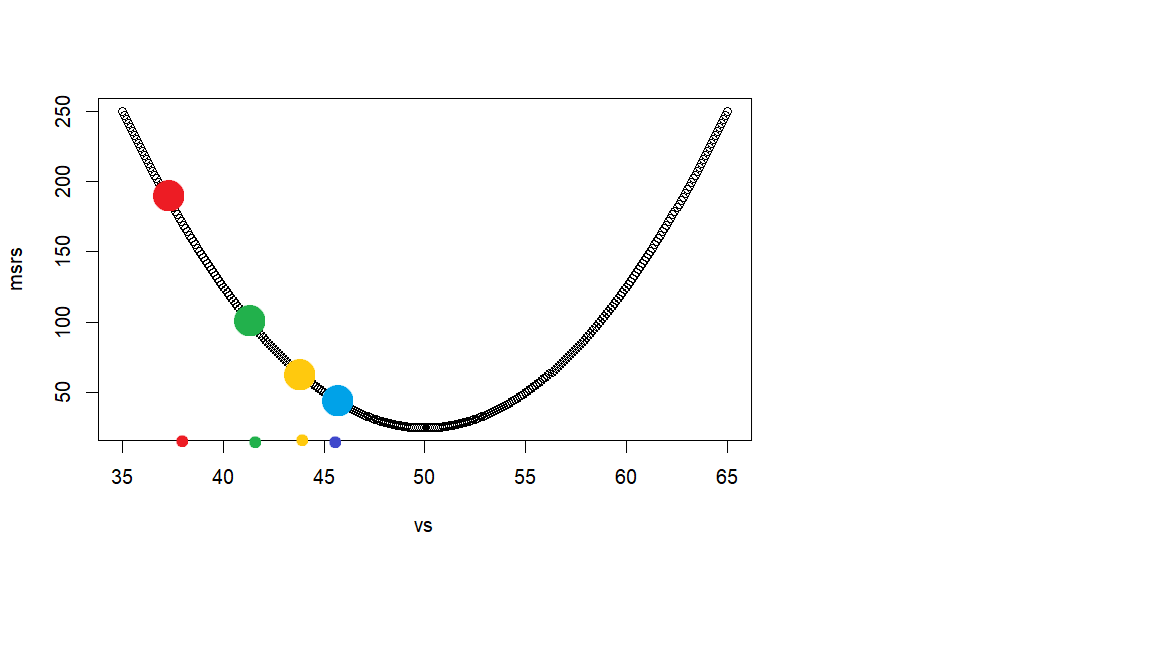
이 R script의 목적은 v값이 최소값이 되는 지점을 자동적으로 찾아보려는 것이다. 이것을 위해서 우선 v값으로 사용할 첫 점수를 랜덤하게 구한 후 (아래 그래프에서 빨간색 지점), 자동적으로 그 다음 v 점수를 찾고 (녹색지점), 그 다음 v 점수를 찾고 (황금색 지점), . . . 이런 과정을 계속하면서 각 v 점수에서의 msr값을 구해서 이에 해당하는 v값을 찾아 보려고 한다. 빨간색, 녹색, 황금색, . . . 이를 자동적으로 구하기 위해서 두가지 방법을 사용하는데 그 것이

gradient function과
learning_rate 값이다.

gradient 펑션은 dy/dv 의 연쇄 미분식인 (chain rules) -2(x-v) / n = -2 mean(res) 값을 구하는 것이다. 이렇게 구한 값에 learning_rate값을 곱한후, 이것을 먼저 사용한 v값에서 (빨간색 지점) 빼 주어 다음 v값으로 (녹색지점) 사용하려고 한다. 이 녹색지점에서의 v값을 사용했을 때의 gradient값을 구한 후 다시 이값에 learning_rate인 0.1을 곱하여 그다음 스텝의 값을 얻고, 이 값을 바로 전의 v값에서 빼 준 값을 그 다음 v값으로 사용한다. 이렇게 구하는 v값들은 0.1씩 곱해주는 효과때문에 오른 쪽으로 옮겨가는 지점이 “점진적으로 줄어들게 되고” 이 지점이 msr의 최소값이 되는 지점으로 가게 된다.

클릭하면 큰 이미지로 볼 수 있음

> zx <- (x-mean(x))/sd(x)
> # pick one random v in (x-v)
> v <- rnorm(1)
> 













>

comment

랜덤하게 v값을 찾음 v ← rnorm(1)
원래는 mean(x)값 근처의 값을 랜덤하게 골라야 하므로
v ← rnorm(1, mean(x), sd(x)) 와 같이 써야 하지만 (현재의 경우, rnorm(1, 50, 5) 가 된다)
그렇게 하질 않고 x 집합의 원소들을 표준점수화 한 후 zx ← (x-mean(x))/sd(x) (이렇게 표준점수화 하면 x 변인의 평균이 0, 표준편차가 1 이 되는 집합으로 변한다)
v ← rnorm(1, 0, 1) 로 구한다. 뒤의 인자인 0, 1 은 default이모로 생략.
이렇게 하는 이유는 혹시 나중에 다른 x집합에 똑같은 작업을 하더라도 그 집합의 평균과 표준편차를 사용하지 않고
단순히 rnorm(1) 을 이용해서 찾으려고 하는 것이다.

> # Train the model with scaled features
> learning.rate = 1e-1
>

comment

이 0.1은 gradient function으로 구한 해당 v값에 대한 y 미분값을 (기울기 값을) 구한 후, 여기에 곱하기 위해서 지정한다.

> msrs <- c()
> vs <- c()
> 
> nlen <- 75
> for (epoch in 1:nlen) {
+     residual <- residuals(zx, v)
+     msr.x <- msr(zx, v)
+     msrs <- append(msrs, msr.x)
+     
+     grad <- gradient(zx, v)
+     step.v <- grad * learning.rate # 
+     v <- v - step.v # 그 다음 v값
+     vs <- append(vs, v) # v값 저장
+ }
> 
> tail(msrs)
[1] 0.999 0.999 0.999 0.999 0.999 0.999
> tail(vs)
[1] 6.415945e-08 5.132756e-08 4.106205e-08 3.284964e-08 2.627971e-08 2.102377e-08
> 
> plot(vs, msrs)
> 
>

comment

nlen는 그냥 자의적으로 지정한다. 여기서는 75로 했다.
for 문에서 처음 v값은 위에서 랜덤으로 구한 값이다 (v).
이 v값으로 gradient 펑션의 아웃풋 값을 구하고 (-2(residual)) = grad ← gradient(x, v)
이 값에 learning_rate값을 곱한 값을 구하여 step.v ← grad * learaning_rate
이 값을 원래 v값에서 빼준 후에
다시 (for 문에서 반복하는 동안) v값으로 바꾼 후 v ← v - step.v
for문을 nlen번 만큼 반복한다.
이 과정에서 저장한
msr값들과
vs값들의 마지막 6개를 살펴본다.
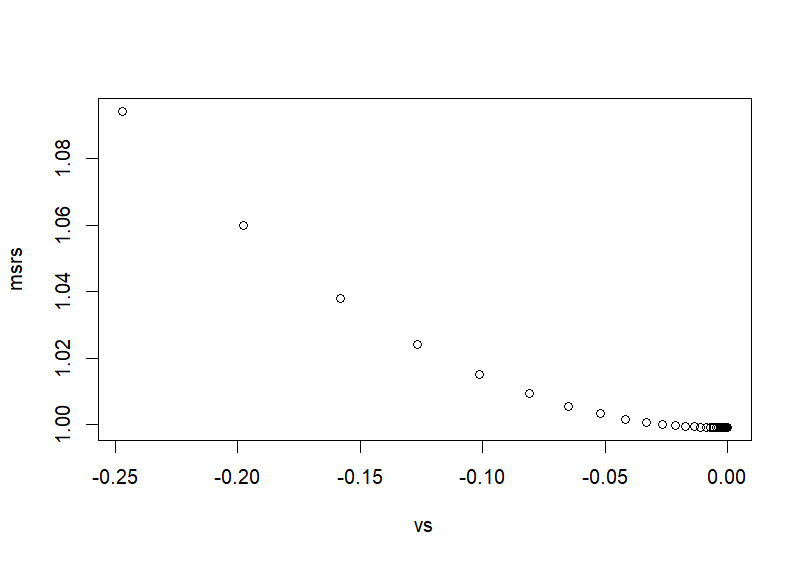
v 값으로 x집합의 평균값을 사용하는 것이 최소 msr값이 된다는 것이 맞다면
v 값은 0이 될것이다 (왜냐하면 x집합을 zx로 바꿨기 때문에, 즉 평균이 0이고 sd값이 1일 집합으로 바꿨기 때문에)
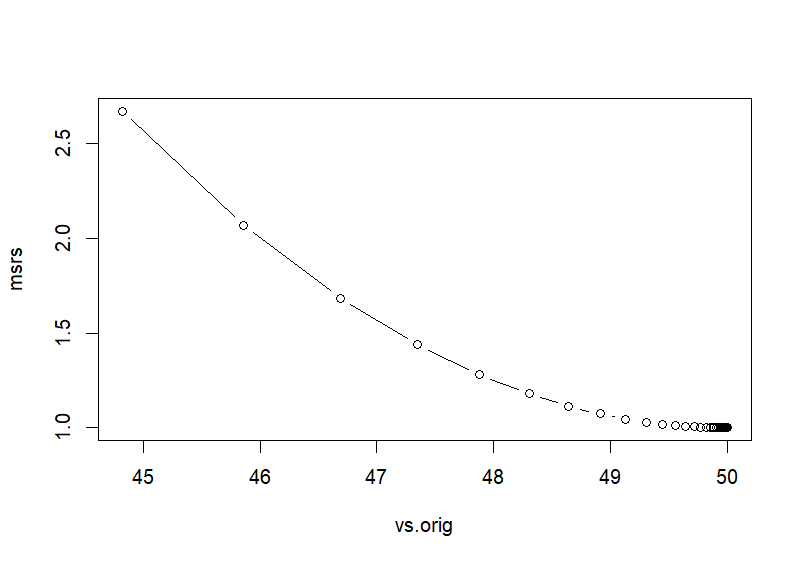
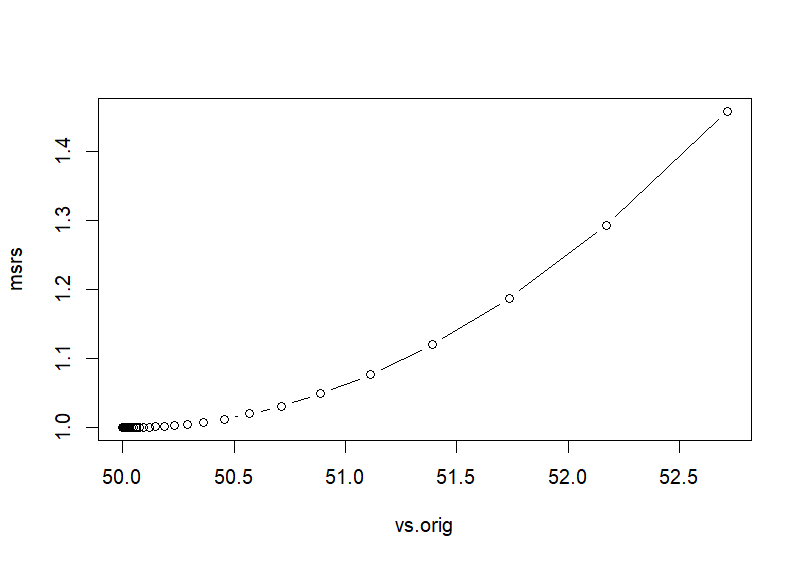
아래 그래프의 각 포인트는 v값의 이동을 나타내는데 grad*learning_rate의 영향으로 점진적으로 하가하여 최소값으로 도달한다.

> # scaled
> vs # 변화하는 v 값들의 집합 
 [1] 3.119260e-01 2.495408e-01 1.996326e-01 1.597061e-01 1.277649e-01 1.022119e-01 8.176952e-02
 [8] 6.541561e-02 5.233249e-02 4.186599e-02 3.349279e-02 2.679424e-02 2.143539e-02 1.714831e-02
[15] 1.371865e-02 1.097492e-02 8.779935e-03 7.023948e-03 5.619158e-03 4.495327e-03 3.596261e-03
[22] 2.877009e-03 2.301607e-03 1.841286e-03 1.473029e-03 1.178423e-03 9.427383e-04 7.541907e-04
[29] 6.033525e-04 4.826820e-04 3.861456e-04 3.089165e-04 2.471332e-04 1.977066e-04 1.581652e-04
[36] 1.265322e-04 1.012258e-04 8.098061e-05 6.478449e-05 5.182759e-05 4.146207e-05 3.316966e-05
[43] 2.653573e-05 2.122858e-05 1.698286e-05 1.358629e-05 1.086903e-05 8.695226e-06 6.956181e-06
[50] 5.564945e-06 4.451956e-06 3.561565e-06 2.849252e-06 2.279401e-06 1.823521e-06 1.458817e-06
[57] 1.167054e-06 9.336428e-07 7.469143e-07 5.975314e-07 4.780251e-07 3.824201e-07 3.059361e-07
[64] 2.447489e-07 1.957991e-07 1.566393e-07 1.253114e-07 1.002491e-07 8.019931e-08 6.415945e-08
[71] 5.132756e-08 4.106205e-08 3.284964e-08 2.627971e-08 2.102377e-08
> vs.orig <- (vs*sd(x))+mean(x) 
> vs.orig
 [1] 51.55963 51.24770 50.99816 50.79853 50.63882 50.51106 50.40885 50.32708 50.26166 50.20933
[11] 50.16746 50.13397 50.10718 50.08574 50.06859 50.05487 50.04390 50.03512 50.02810 50.02248
[21] 50.01798 50.01439 50.01151 50.00921 50.00737 50.00589 50.00471 50.00377 50.00302 50.00241
[31] 50.00193 50.00154 50.00124 50.00099 50.00079 50.00063 50.00051 50.00040 50.00032 50.00026
[41] 50.00021 50.00017 50.00013 50.00011 50.00008 50.00007 50.00005 50.00004 50.00003 50.00003
[51] 50.00002 50.00002 50.00001 50.00001 50.00001 50.00001 50.00001 50.00000 50.00000 50.00000
[61] 50.00000 50.00000 50.00000 50.00000 50.00000 50.00000 50.00000 50.00000 50.00000 50.00000
[71] 50.00000 50.00000 50.00000 50.00000 50.00000
> 
> # 마지막 v값이 최소값에 근접한 값
> v 
[1] 2.102377e-08
> v.orig <- (v*sd(x))+mean(x) 
> v.orig
[1] 50
>
> plot(vs.orig, msrs, type='b')
> 
> 
>

comment

만약에 처음에 구한 랜덤 v값이 평균의 오른 쪽에있었더라면, 아래 그림과 같이 평균에 접근했을 것이다.

그렇다면 왜 n-2 혹은 n-(1/2)가 아니고 n-1인가? 이를 수학적인 증명을 통해서 살펴보면 다음 장과 같다.

수학적 증명

우선,

\begin{eqnarray*} Var[X] & = & E[(X-\mu)^{2}] \\ & = & E[(X^{2} - 2 X \mu + \mu^{2})] \\ & = & E[X^{2}] - 2 \mu E[X] + E[\mu^2] \\ & = & E[X^{2}] - 2 \mu E[X] + E[\mu^{2}], \;\; \text{because}\; E[X] = \mu \text{, } \; E[\mu^2] = \mu^2, \\ & = & E[X^{2}] - 2 \mu^{2} + \mu^{2} \\ & = & E[X^{2}] - \mu^{2} \end{eqnarray*}

이므로

\begin{align} E\left[X^2\right] & = Var\left[X\right] + \mu^2 \nonumber \\ & = \sigma^{2} + \mu^2 \\ \end{align}

마찬가지로
\begin{align} Var \left[ \overline{X}\right] & = E \left[\overline{X}^2 \right] - \left[E(\overline{X})\right]^2 \nonumber \\ & = E\left[\overline{X}^{2}\right] - \mu^{2} \nonumber \end{align}

따라서
\begin{align} E\left[\overline{X}^{2}\right] & = Var\left[\overline{X}\right] + \mu^2 \nonumber \\ & = \frac {\sigma^{2}} {n} + \mu^{2} \end{align}

참고로 위에서 $Var\left[\overline{X}\right] = \dfrac {\sigma^{2}} {n} $ 에 해당하는 설명은 mean and variance of the sample mean 문서를 볼 것.

참고로 Expected value (기대값)와 Variance (분산)의 연산에 과한 법칙으로는 ²⁾

X,Y are Independent variables.

\begin{align*} E[aX] & = a E[X] \\ E[X+Y] & = E[X] + E[Y] \\ Var[aX] & = a^{\tiny{2}} Var[X] \\ Var[X+Y] & = Var[X] + Var[Y] \end{align*}

우리가 알고자 하는 것은 아래의 식이 population의 parameter인 $\sigma^{2}$ 의 값과 같은가이다.
\begin{align*} E[s^{2}] & = E \left[\frac{\displaystyle\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}{n-1} \right] \qquad \cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot \;\; (a) \\ & = \sigma^{2} \end{align*}

위의 식에서 일부만을 추출해서 먼저 보자.

\begin{align*} E \left[\sum{(X_{i}-\overline{X})^{2}} \right] & = E \left[\sum(X_{i}^{2}- 2 X_{i} \overline{X} + \overline{X}^{2})\right] \\ & = E \left[ \sum{X_{i}^2} - \sum{2X_{i} \overline{X}} + \sum {\overline{X^2}} \right] \\ & = E \left[ \sum{X_{i}^2} - 2 \overline{X} \sum{X_{i}} + \sum{\overline{X^2}} \right] \\ & = E \left[ \sum{X_{i}^2} - 2 \overline{X} \sum{X_{i}} + n \overline{X^2} \right] \\ & = E \left[ \sum{X_{i}^2} - 2 \overline{X} \cdot (n \overline{X}) + n \overline {X^2} \right] \\ & = E \left[ \sum{X_{i}^2} - n \overline{X}^2 \right] \\ & = \sum {E\left(X_{i}^2\right)} - E\left(n\overline{X}^2\right) \\ & = \sum {E\left(X_{i}^2\right)} - n E\left(\overline{X}^2\right) \;\;\; \dots\dots\dots\dots\dots (3) \end{align*}

한 편, 위의 $(1), (2)$에서

\begin{align*} E\left[X_{i}^{2}\right] & = \sigma^{2} + \mu^2 \;\;\; \dots\dots\dots\dots\dots (1) \\ E\left[\overline{X}^{2}\right] & = \dfrac {\sigma^{2}} {n} + \mu^{2} \;\;\; \dots\dots\dots\dots\dots (2) \end{align*}

위의 $(1), (2)$를 $(3)$에 대입해보면

\begin{align*} E \left[\sum{(X_{i}-\overline{X})^{2}} \right] & = \sum{E\left(X_{i}^{2}\right)} - n E\left(\overline{X}^{2}\right) \\ & = \sum{\left(\sigma^{2} + \mu^{2}\right)} - n \left(\dfrac{\sigma^2}{n} + \mu^2\right) \\ & = n\sigma^{2} + n\mu^{2} - \sigma^{2} - n\mu^{2} \\ & = \left(n-1\right) \sigma^{2} \end{align*}

위는 식 (a)의 일부이므로 이를 온전한 식에 대입해보면,
\begin{eqnarray*} E \left[\sum{(X_{i}-\overline{X})^{2}} \right] & = & (n-1) \sigma^{2} \\ \end{eqnarray*}

\begin{eqnarray*} E[s^{2}] & = & E \left[ \frac{\displaystyle\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}}{n-1} \right] \\ & = & \dfrac{1}{n-1} E \left[\sum{(X_{i}-\overline{X})^{2}} \right] \\ & = & \dfrac{1}{n-1} (n-1) \sigma^{2} \\ & = & \sigma^{2} \end{eqnarray*}

그러므로, n-1로 나눠 준 샘플분산의 (sample's variance) 기대값은
\begin{eqnarray*} E(s^2) = \sigma^{2} \end{eqnarray*}

만약에 우리가 population의 variance를 구하듯이 n을 이용한다고 하면,

\begin{eqnarray*} E[s^{2}] & = & E \left[ \frac{\displaystyle\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}} {n} \right], \;\;\; \text{note that we use n instead of n-1} \\ & = & \dfrac{1}{n} E \left[\sum{(X_{i}-\overline{X})^{2}} \right] \\ & = & \dfrac{1}{n} (n-1) \sigma^{2} \\ & = & \left(\dfrac{n-1}{n}\right) \sigma^{2} \\ \end{eqnarray*}

즉, 원래 $\sigma^2$ 값보다 조금 작은 값을 갖게 될 것이다 (이를 biased result라고 한다). 따라서 샘플을 취한 후에 모집단의 분산을 추정할 때에는 n 대신에 n-1을 사용하는 것이 맞다. 그렇다면 모집단의 분산을 구할 때는 n으로 (N으로) 나누어 주면 된다고 생각된다. 그러나 일반적으로 모집단의 분산을 구할 때에도 N-1로 나누어 구하게 된다. 이유는 모집단의 경우에 N이 충분히 큰 경우인데 이 때에는 N으로 나누어 주나, N-1로 나누어주나 큰 차이가 없기 때문이다. 따라서, R에서 분산을 구하는 var(x)에는 x의 성격에 상관없이 SS를 n-1로 나누어 분산을 구하게 된다.

COMMunication
RESearch.NET

Table of Contents

Why n-1

직관적 이해

실험적, R에서 시뮬레이션으로 이해

output

R에서 msr이 최소값이 되는 v값 효율적으로 찾기

output

수학적 증명

tags