krackhardt_datasets
Table of Contents
Krackhardt Datasets
Krackhardt dataset in NetData packages
Analysis of Structural Features with advice and reports to data
install.packages("NetData")
# install.packages("igraph")
library(NetData)
library(igraph)
data(package="NetData")
data(kracknets, package = "NetData")
head(krack_full_data_frame)
> head(krack_full_data_frame) ego alter advice_tie friendship_tie reports_to_tie 1 1 1 0 0 0 2 1 2 1 1 1 3 1 3 0 0 0 4 1 4 1 1 0 5 1 5 0 0 0 6 1 6 0 0 0 >
krack_full_nonzero_edges <- subset(krack_full_data_frame, (friendship_tie > 0 | advice_tie > 0 | reports_to_tie > 0)) head(krack_full_nonzero_edges)
> krack_full_nonzero_edges <- subset(krack_full_data_frame, (friendship_tie > 0 | advice_tie > 0 | reports_to_tie > 0)) > head(krack_full_nonzero_edges) ego alter advice_tie friendship_tie reports_to_tie 2 1 2 1 1 1 4 1 4 1 1 0 8 1 8 1 1 0 12 1 12 0 1 0 16 1 16 1 1 0 18 1 18 1 0 0 >
subset function은 1 10 0 0 0 와 같은 데이터 열을 제외하려고 사용
################################################# # data frame 형식의 krack_full_nonzero_edges # (원 데이터가 data.frame형식의 # krack_full_data_frame이었음)을 # igraph 포맷의 graph로 변환함 (graph.data.frame) ################################################# krack_full <- graph.data.frame(krack_full_nonzero_edges) summary(krack_full)
> krack_full <- graph.data.frame(krack_full_nonzero_edges) > summary(krack_full) IGRAPH 750f8b3 DN-- 21 232 -- + attr: name (v/c), advice_tie (e/n), friendship_tie (e/n), reports_to_tie (e/n) >
krack_friend <- delete_edges(krack_full, E(krack_full)[E(krack_full)$friendship_tie==0]) summary(krack_friend) krack_friend[] krack_advice <- delete_edges(krack_full, E(krack_full)[E(krack_full)$advice_tie==0]) summary(krack_advice) krack_advice[] krack_reports_to <- delete_edges(krack_full, E(krack_full)[E(krack_full)$reports_to_tie==0]) summary(krack_reports_to) krack_reports_to[]
krack_friend <- delete.edges(krack_full, E(krack_full)[E(krack_full)$friendship_tie==0])
> summary(krack_friend)
IGRAPH 9c78e3a DN-- 21 102 --
+ attr: name (v/c), advice_tie (e/n), friendship_tie (e/n),
| reports_to_tie (e/n)
> krack_friend[]
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . 1 . . . 1 . . . . .
2 1 . . . . . . . . . . . . . . . . 1 . . 1
3 . . . . . . . . . . . . . 1 . . . . 1 . .
4 1 1 . . . . . 1 . . . 1 . . . 1 1 . . . .
5 . 1 . . . . . . 1 . 1 . . 1 . . 1 . 1 . 1
6 . 1 . . . . 1 . 1 . . 1 . . . . 1 . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . 1 . . . . . . . . . . . . . . . . .
9 . . . . . . . . . . . . . . . . . . . . .
10 . . 1 . 1 . . 1 1 . . 1 . . . 1 . . . 1 .
11 1 1 1 1 1 . . 1 1 . . 1 1 . 1 . 1 1 1 . .
12 1 . . 1 . . . . . . . . . . . . 1 . . . 1
13 . . . . 1 . . . . . 1 . . . . . . . . . .
14 . . . . . . 1 . . . . . . . 1 . . . . . .
15 1 . 1 . 1 1 . . 1 . 1 . . 1 . . . . 1 . .
16 1 1 . . . . . . . . . . . . . . . . . . .
17 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 . . 1 1 1
18 . 1 . . . . . . . . . . . . . . . . . . .
19 1 1 1 . 1 . . . . . 1 1 . 1 1 . . . . 1 .
20 . . . . . . . . . . 1 . . . . . . 1 . . .
21 . 1 . . . . . . . . . 1 . . . . 1 1 . . .
>
> krack_advice <- delete.edges(krack_full, E(krack_full)[E(krack_full)$advice_tie==0])
> summary(krack_advice)
IGRAPH 9c7adf4 DN-- 21 190 --
+ attr: name (v/c), advice_tie (e/n), friendship_tie (e/n),
| reports_to_tie (e/n)
> krack_advice[]
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . . . . . 1 . 1 . . 1
2 . . . . . 1 1 . . . . . . . . . . . . . 1
3 1 1 . 1 . 1 1 1 1 1 1 1 . 1 . . 1 1 . 1 1
4 1 1 . . . 1 . 1 . 1 1 1 . . . 1 1 1 . 1 1
5 1 1 . . . 1 1 1 . 1 1 . 1 1 . 1 1 1 1 1 1
6 . . . . . . . . . . . . . . . . . . . . 1
7 . 1 . . . 1 . . . . 1 1 . 1 . . 1 1 . . 1
8 . 1 . 1 . 1 1 . . 1 1 . . . . . . 1 . . 1
9 1 1 . . . 1 1 1 . 1 1 1 . 1 . 1 1 1 . . 1
10 1 1 1 1 1 . . 1 . . 1 . 1 . 1 1 1 1 1 1 .
11 1 1 . . . . 1 . . . . . . . . . . . . . .
12 . . . . . . 1 . . . . . . . . . . . . . 1
13 1 1 . . 1 . . . 1 . . . . 1 . . . 1 . . .
14 . 1 . . . . 1 . . . . . . . . . . 1 . . 1
15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1
16 1 1 . . . . . . . 1 . . . . . . . 1 . . .
17 1 1 . 1 . . 1 . . . . . . . . . . . . . 1
18 1 1 1 1 1 . 1 1 1 1 1 . 1 1 1 1 . . 1 1 1
19 1 1 1 . 1 . 1 . . 1 1 . . 1 1 . . 1 . 1 .
20 1 1 . . . 1 . 1 . . 1 1 . 1 1 1 1 1 . . 1
21 . 1 1 1 . 1 1 1 . . . 1 . 1 . . 1 1 . 1 .
>
> krack_reports_to <- delete.edges(krack_full, E(krack_full)[E(krack_full)$reports_to_tie==0])
> summary(krack_reports_to)
IGRAPH 9c7cb3e DN-- 21 20 --
+ attr: name (v/c), advice_tie (e/n), friendship_tie (e/n),
| reports_to_tie (e/n)
> krack_reports_to[]
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . . . . . . . . . . . . . . . . . . .
2 . . . . . . 1 . . . . . . . . . . . . . .
3 . . . . . . . . . . . . . 1 . . . . . . .
4 . 1 . . . . . . . . . . . . . . . . . . .
5 . . . . . . . . . . . . . 1 . . . . . . .
6 . . . . . . . . . . . . . . . . . . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . . . . . . . . . . . . . . . . . . 1
9 . . . . . . . . . . . . . 1 . . . . . . .
10 . . . . . . . . . . . . . . . . . 1 . . .
11 . . . . . . . . . . . . . . . . . 1 . . .
12 . . . . . . . . . . . . . . . . . . . . 1
13 . . . . . . . . . . . . . 1 . . . . . . .
14 . . . . . . 1 . . . . . . . . . . . . . .
15 . . . . . . . . . . . . . 1 . . . . . . .
16 . 1 . . . . . . . . . . . . . . . . . . .
17 . . . . . . . . . . . . . . . . . . . . 1
18 . . . . . . 1 . . . . . . . . . . . . . .
19 . . . . . . . . . . . . . 1 . . . . . . .
20 . . . . . . . . . . . . . 1 . . . . . . .
21 . . . . . . 1 . . . . . . . . . . . . . .
>
par(mfrow = c(1,3)) krack_friend_layout <- layout.fruchterman.reingold(krack_friend) plot(krack_friend, layout=krack_friend_layout, main = "friend", edge.arrow.size=.5) krack_advice_layout <- layout.fruchterman.reingold(krack_advice) plot(krack_advice, layout=krack_advice_layout, main = "advice", edge.arrow.size=.5) krack_reports_to_layout <- layout.fruchterman.reingold(krack_reports_to) plot(krack_reports_to, layout=krack_reports_to_layout, main = "reports to", edge.arrow.size=.5) par(mfrow = c(1,1))
# We'll use the "task" and "social" sub-graphs together as the # basis for our structural equivalence methods. First, we'll use # the task graph to generate an adjacency matrix. # # This matrix represents task interactions directed FROM the # row individual TO the column individual. krack_reports_to_matrix_row_to_col <- get.adjacency(krack_reports_to, attr='reports_to_tie') krack_reports_to_matrix_row_to_col # To operate on a binary graph, simply leave off the "attr" # parameter: krack_reports_to_matrix_row_to_col_bin <- get.adjacency(krack_reports_to) krack_reports_to_matrix_row_to_col_bin # For this lab, we'll use the valued graph. The next step is to # concatenate it with its transpose in order to capture both # incoming and outgoing task interactions. krack_reports_to_matrix_col_to_row <- t(as.matrix(krack_reports_to_matrix_row_to_col)) krack_reports_to_matrix_col_to_row krack_reports_to_matrix <- rbind(krack_reports_to_matrix_row_to_col, krack_reports_to_matrix_col_to_row) krack_reports_to_matrix
# Next, we'll use the same procedure to add advice # information. krack_advice_matrix_row_to_col <- get.adjacency(krack_advice, attr='advice_tie') krack_advice_matrix_row_to_col krack_advice_matrix_row_to_col_bin <- get.adjacency(krack_advice) krack_advice_matrix_row_to_col_bin krack_advice_matrix_col_to_row <- t(as.matrix(krack_advice_matrix_row_to_col)) krack_advice_matrix_col_to_row krack_advice_matrix <- rbind(krack_advice_matrix_row_to_col, krack_advice_matrix_col_to_row) krack_advice_matrix
krack_friend_matrix_row_to_col <- get.adjacency(krack_friend, attr='friendship_tie') krack_friend_matrix_row_to_col # To operate on a binary graph, simply leave off the "attr" # parameter: krack_friend_matrix_row_to_col_bin <- get.adjacency(krack_friend) krack_friend_matrix_row_to_col_bin # For this lab, we'll use the valued graph. The next step is to # concatenate it with its transpose in order to capture both # incoming and outgoing task interactions. krack_friend_matrix_col_to_row <- t(as.matrix(krack_friend_matrix_row_to_col)) krack_friend_matrix_col_to_row krack_friend_matrix <- rbind(krack_friend_matrix_row_to_col, krack_friend_matrix_col_to_row) krack_friend_matrix
# ra (ar) krack_reports_to_advice_matrix <- rbind(krack_reports_to_matrix, krack_advice_matrix) krack_reports_to_advice_matrix # fa krack_friend_advice_matrix <- rbind(krack_friend_matrix, krack_advice_matrix) krack_friend_advice_matrix # fr krack_friend_reports_to_matrix <- rbind(krack_friend_matrix, krack_reprots_to_matrix) krack_friend_reports_to_matrix # far krack_friend_advice_reports_to_matrix <- rbind(krack_friend_advice_matrix, krack_reports_to_matrix) krack_friend_advice_reports_to_matrix
# Now we have a single 4n x n matrix that represents both in- and # out-directed task and social communication. From this, we can # generate an n x n correlation matrix that shows the degree of # structural equivalence of each actor in the network. krack_reports_to_advice_cors <- cor(as.matrix(krack_reports_to_advice_matrix)) krack_reports_to_advice_cors krack_friend_advice_cors <- cor(as.matrix(krack_friend_advice_matrix)) krack_friend_advice_cors krack_friend_reports_to_cors <- cor(as.matrix(krack_friend_reports_to_matrix)) krack_friend_reports_to_cors krack_friend_advice_reports_to_cors <- cor(as.matrix(krack_friend_advice_reports_to_matrix)) krack_friend_advice_reports_to_cors
# To use correlation values in hierarchical NetCluster, they must
# first be coerced into a "dissimilarity structure" using dist().
# We subtract the values from 1 so that they are all greater than
# or equal to 0; thus, highly dissimilar (i.e., negatively
# correlated) actors have higher values.
dissimilarity_ra <- 1 - krack_reports_to_advice_cors
krack_reports_to_advice_dist <- as.dist(dissimilarity_ra)
krack_reports_to_advice_dist
dissimilarity_fa <- 1 - krack_friend_advice_cors
krack_friend_advice_dist <- as.dist(dissimilarity_fa)
krack_friend_advice_dist
dissimilarity_rf <- 1 - krack_reports_to_friend_cors
krack_reports_to_friend_dist <- as.dist(dissimilarity_rf)
krack_reports_to_friend_dist
dissimilarity_far <- 1 - krack_friend_advice_reports_to_cors
krack_friend_advice_reports_to_dist <- as.dist(dissimilarity_far)
krack_friend_advice_reports_to_dist
# Note that it is also possible to use dist() directly on the
# matrix. However, since cor() looks at associations between
# columns and dist() looks at associations between rows, it is
# necessary to transpose the matrix first.
#
# A variety of distance metrics are available; Euclidean
# is the default.
#m182_task_social_dist <- dist(t(m182_task_social_matrix))
#m182_task_social_dist
# hclust() performs a hierarchical agglomerative NetCluster
# operation based on the values in the dissimilarity matrix
# yielded by as.dist() above. The standard visualization is a
# dendrogram. By default, hclust() agglomerates clusters via a
# "complete linkakage" algorithm, determining cluster proximity
# by looking at the distance of the two points across clusters
# that are farthest away from one another. This can be changed via
# the "method" parameter.
krack_reports_to_advice_hclust <- hclust(krack_reports_to_dist)
plot(krack_reports_to_advice_hclust)
# cutree() allows us to use the output of hclust() to set
# different numbers of clusters and assign vertices to clusters
# as appropriate. For example:
cutree(krack_reports_to_advice_hclust, k=2)
# Now we'll try to figure out the number of clusters that best
# describes the underlying data. To do this, we'll loop through
# all of the possible numbers of clusters (1 through n, where n is
# the number of actors in the network). For each solution
# corresponding to a given number of clusters, we'll use cutree()
# to assign the vertices to their respective clusters
# corresponding to that solution.
#
# From this, we can generate a matrix of within- and between-
# cluster correlations. Thus, when there is one cluster for each
# vertex in the network, the cell values will be identical to the
# observed correlation matrix, and when there is one cluster for
# the whole network, the values will all be equal to the average
# correlation across the observed matrix.
#
# We can then correlate each by-cluster matrix with the observed
# correlation matrix to see how well the by-cluster matrix fits
# the data. We'll store the correlation for each number of
# clusters in a vector, which we can then plot.
# First, we initialize a vector for storing the correlations and
# set a variable for our number of vertices.
clustered_observed_cors = vector()
num_vertices = length(V(krack_reports_to))
# Next, we loop through the different possible cluster
# configurations, produce matrices of within- and between-
# cluster correlations, and correlate these by-cluster matrices
# with the observed correlation matrix.
# pdf("6.3_m182_studentnet_task_social_clustered_observed_corrs.pdf")
clustered_observed_cors <-clustConfigurations(num_vertices, krack_reports_to_advice_hclust, krack_reports_to_advice_cors)
clustered_observed_cors
plot(clustered_observed_cors$correlations)
# dev.off()
clustered_observed_cors$correlations
# From a visual inspection of the correlation matrix, we can
# decide on the proper number of clusters in this network.
# For this network, we'll use 4. (Note that the 1-cluster
# solution doesn't appear on the plot because its correlation
# with the observed correlation matrix is undefined.)
num_clusters = 4
clusters <- cutree(krack_reports_to_advice_hclust, k = num_clusters)
clusters
cluster_cor_mat <- clusterCorr(krack_reports_to_advice_cors,
clusters)
cluster_cor_mat
# Let's look at the correlation between this cluster configuration
# and the observed correlation matrix. This should match the
# corresponding value from clustered_observed_cors above.
gcor(cluster_cor_mat, krack_reports_to_advice_cors)
#####################
# Questions:
# (1) What rationale do you have for selecting the number of
# clusters / positions that you do?
#####################
### NOTE ON DEDUCTIVE CLUSTERING
# It's pretty straightforward, using the code above, to explore
# your own deductive NetCluster. Simply supply your own cluster
# vector, where the elements in the vector are in the same order
# as the vertices in the matrix, and the values represent the
# cluster to which each vertex belongs.
#
# For example, if you believed that actors 2, 7, and 8 formed one
# group, actor 16 former another group, and everyone else formed
# a third group, you could represent this as follows:
deductive_clusters = c(1, 2, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1,
1, 3)
# You could then examine the fitness of this cluster configuration
# as follows:
deductive_cluster_cor_mat <- generate_cluster_cor_mat(
krack_reports_to_advice_cors,
deductive_clusters)
deductive_cluster_cor_mat
gcor(deductive_cluster_cor_mat, krack_reports_to_advice_cors)
### END NOTE ON DEDUCTIVE CLUSTERING
# Now we'll use the 4-cluster solution to generate blockmodels,
# using the raw tie data from the underlying task and social
# networks.
# Task valued
task_mean <- mean(as.matrix(krack_reports_to_matrix_row_to_col)_
task_mean
task_valued_blockmodel <- blockmodel(krack_reports_to_matrix_row_to_col, clusters)
task_valued_blockmodel
# Task binary
task_density <- graph.density(krack_reports_to)
task_density
task_binary_blockmodel <- blockmodel(as.matrix(krack_reports_to_matrix_row_to_col_bin), clusters)
task_binary_blockmodel
# Social valued
advice_mean <- mean(as.matrix(krack_advice_matrix_row_to_col))
advice_mean
advice_valued_blockmodel <- blockmodel(as.matrix(krack_advice_matrix_row_to_col), clusters)
advice_valued_blockmodel
# Social binary
advice_density <- graph.density(krack_advice)
advice_density
advice_binary_blockmodel <- blockmodel(as.matrix(krack_advice_matrix_row_to_col_bin), clusters)
advice_binary_blockmodel
# We can also permute the network to examine the within- and
# between-cluster correlations.
cluster_cor_mat_per <- permute_matrix(clusters, cluster_cor_mat)
cluster_cor_mat_per
#####################
# Questions:
# (2) What is the story you get from viewing these clusters,
# and their within and between cluster densities on task and
# social interaction? What can you say about M182 from this?
#####################
#####################
# Questions:
# (3) What does clustering of the triadic census afford us?
# What roles do you see? Redo the initial blockmodel analysis
# without social interaction (only task) and then compare to
# this solution. Do they differ?
#
# Extra credit: Try running the triad census on task AND
# social interaction separately and then correlating persons.
# What result do you get? Is it different from our initial
# blockmodel result? Show your code.
######################
###
# 5. FACTOR ANALYSIS
###
# Note that although we are conducting a principal components
# analysis (PCA), which is technically not exactly the same as
# factor analysis, we will use the term "factor" to describe the
# individual components in our PCA.
# PCA is often used in network analysis as a form of detecting
# individuals global positioning. We say "global" because these
# clusters aren't defined on local cohesion but from the overall
# pattern of ties individuals have with all others (structural
# equivalence). Identifying the first two largest components that
# organize the variance in tie patterns is one way of doing this.
# We'll analyze the 4n x n matrix generated above.
# First, we want to determine the ideal number of components
# (factors) to extract. We'll do this by examining the eigenvalues
# in a scree plot and examining how each number of factors stacks
# up to a few proposed non-graphical solutions to selecting the
# optimal number of components, available via the nFactors
# package.
ev <- eigen(cor(as.matrix(krack_reports_to_advice_matrix))) # get eigenvalues
ap <- parallel(subject=nrow(krack_reports_to_advice_matrix),
var=ncol(krack_reports_to_advice_matrix),
rep=100,cent=.05)
nS <- nScree(ev$values, ap$eigen$qevpea)
# pdf("6.6_m182_studentnet_task_social_pca_scree.pdf")
plotnScree(nS)
# To draw a line across the graph where eigenvalues are = 1,
# use the following code:
plotnScree(nS)
abline(h=1)
# dev.off()
# For more information on this procedure, please see
# the references provided in the parallel() documentation
# (type "?parallel" in the R command line with the package
# loaded).
# Now we'll run a principal components analysis on the matrix,
# using the number of factors determined above (note this may not
# be the same number as you get):
pca_krack_reports_to_advice = principal(as.matrix(krack_reports_to_advice_matrix), nfactors=5, rotate="varimax")
# Let's take a look at the results in the R terminal:
pca_krack_reports_to_advice
# You can see the standardized loadings for each factor for each
# node. Note that R sometimes puts the factors in a funky order
# (e.g. RC1, RC2, RC5, RC4, RC3) but all of the factors are there.
# You can see that the SS loadings, proportion of variance
# explained and cumulative variance explained is provided below. A
# Chi Square test of the factors and various other statistics are
# provided below.
# Note that the eigenvalues can be accessed via the following
# command:
pca_krack_reports_to_advice$values
# Now we will use the factor loadings to cluster and compare that
# to our other NetCluster techniques, using dendrograms.
# Take the distance based on Euclidian Distance
krack_reports_to_factor_dist = dist(pca_krack_reports_to_advice$loadings)
# And cluster
krack_reports_to_factor_hclust <- hclust(krack_reports_to_factor_dist)
# pdf("6.7_m182_studentnet_task_social_pca_hclust.pdf")
plot(krack_reports_to_factor_hclust)
# dev.off()
# And compare to NetCluster based on correlations and triads:
# pdf("6.8_m182_task_cluster_by_correlation_PCA_Triads.pdf")
par(mfrow = c(1,2))
plot(krack_reports_to_advice_hclust, main = "Correlation")
plot(krack_reports_to_factor_hclust, main = "PCA")
# plot(m182_task_triad_hclust, main = "Triads")
par(mfrow = c(1,1))
# dev.off()
#####################
# Questions:
# (4) How do the results across blockmodel techniques differ?
# Why might you use one over the other? Why might you want to
# run more than one in your analyses?
#####################
Analysis based on friendship and advice data
preparation
install.packages("NetData")
# install.packages("igraph")
library(NetData)
library(igraph)
data(package="NetData")
data(kracknets, package = "NetData")
head(krack_full_data_frame)
> head(krack_full_data_frame) ego alter advice_tie friendship_tie reports_to_tie 1 1 1 0 0 0 2 1 2 1 1 1 3 1 3 0 0 0 4 1 4 1 1 0 5 1 5 0 0 0 6 1 6 0 0 0 >
krack_full_nonzero_edges <- subset(krack_full_data_frame, (friendship_tie > 0 | advice_tie > 0 | reports_to_tie > 0)) head(krack_full_nonzero_edges)
> krack_full_nonzero_edges <- subset(krack_full_data_frame, (friendship_tie > 0 | advice_tie > 0 | reports_to_tie > 0)) > head(krack_full_nonzero_edges) ego alter advice_tie friendship_tie reports_to_tie 2 1 2 1 1 1 4 1 4 1 1 0 8 1 8 1 1 0 12 1 12 0 1 0 16 1 16 1 1 0 18 1 18 1 0 0 >
subset function은 1 10 0 0 0 와 같은 데이터 열을 제외하려고 사용
################################################# # data frame 형식의 krack_full_nonzero_edges # (원 데이터가 data.frame형식의 # krack_full_data_frame이었음)을 # igraph 포맷의 graph로 변환함 (graph.data.frame) ################################################# krack_full <- graph.data.frame(krack_full_nonzero_edges) summary(krack_full)
> krack_full <- graph.data.frame(krack_full_nonzero_edges) > summary(krack_full) IGRAPH 750f8b3 DN-- 21 232 -- + attr: name (v/c), advice_tie (e/n), friendship_tie (e/n), reports_to_tie (e/n) >
extracting friend, advice, reports_to graph
krack_friend <- delete.edges(krack_full, E(krack_full)[E(krack_full)$friendship_tie==0]) summary(krack_friend) krack_friend[] krack_advice <- delete.edges(krack_full, E(krack_full)[E(krack_full)$advice_tie==0]) summary(krack_advice) krack_advice[] krack_reports_to <- delete.edges(krack_full, E(krack_full)[E(krack_full)$reports_to_tie==0]) summary(krack_reports_to) krack_reports_to[]
krack_friend <- delete.edges(krack_full, E(krack_full)[E(krack_full)$friendship_tie==0])
> summary(krack_friend)
IGRAPH 9c78e3a DN-- 21 102 --
+ attr: name (v/c), advice_tie (e/n), friendship_tie (e/n),
| reports_to_tie (e/n)
> krack_friend[]
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . 1 . . . 1 . . . . .
2 1 . . . . . . . . . . . . . . . . 1 . . 1
3 . . . . . . . . . . . . . 1 . . . . 1 . .
4 1 1 . . . . . 1 . . . 1 . . . 1 1 . . . .
5 . 1 . . . . . . 1 . 1 . . 1 . . 1 . 1 . 1
6 . 1 . . . . 1 . 1 . . 1 . . . . 1 . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . 1 . . . . . . . . . . . . . . . . .
9 . . . . . . . . . . . . . . . . . . . . .
10 . . 1 . 1 . . 1 1 . . 1 . . . 1 . . . 1 .
11 1 1 1 1 1 . . 1 1 . . 1 1 . 1 . 1 1 1 . .
12 1 . . 1 . . . . . . . . . . . . 1 . . . 1
13 . . . . 1 . . . . . 1 . . . . . . . . . .
14 . . . . . . 1 . . . . . . . 1 . . . . . .
15 1 . 1 . 1 1 . . 1 . 1 . . 1 . . . . 1 . .
16 1 1 . . . . . . . . . . . . . . . . . . .
17 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 . . 1 1 1
18 . 1 . . . . . . . . . . . . . . . . . . .
19 1 1 1 . 1 . . . . . 1 1 . 1 1 . . . . 1 .
20 . . . . . . . . . . 1 . . . . . . 1 . . .
21 . 1 . . . . . . . . . 1 . . . . 1 1 . . .
>
> krack_advice <- delete.edges(krack_full, E(krack_full)[E(krack_full)$advice_tie==0])
> summary(krack_advice)
IGRAPH 9c7adf4 DN-- 21 190 --
+ attr: name (v/c), advice_tie (e/n), friendship_tie (e/n),
| reports_to_tie (e/n)
> krack_advice[]
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . . . . . 1 . 1 . . 1
2 . . . . . 1 1 . . . . . . . . . . . . . 1
3 1 1 . 1 . 1 1 1 1 1 1 1 . 1 . . 1 1 . 1 1
4 1 1 . . . 1 . 1 . 1 1 1 . . . 1 1 1 . 1 1
5 1 1 . . . 1 1 1 . 1 1 . 1 1 . 1 1 1 1 1 1
6 . . . . . . . . . . . . . . . . . . . . 1
7 . 1 . . . 1 . . . . 1 1 . 1 . . 1 1 . . 1
8 . 1 . 1 . 1 1 . . 1 1 . . . . . . 1 . . 1
9 1 1 . . . 1 1 1 . 1 1 1 . 1 . 1 1 1 . . 1
10 1 1 1 1 1 . . 1 . . 1 . 1 . 1 1 1 1 1 1 .
11 1 1 . . . . 1 . . . . . . . . . . . . . .
12 . . . . . . 1 . . . . . . . . . . . . . 1
13 1 1 . . 1 . . . 1 . . . . 1 . . . 1 . . .
14 . 1 . . . . 1 . . . . . . . . . . 1 . . 1
15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1
16 1 1 . . . . . . . 1 . . . . . . . 1 . . .
17 1 1 . 1 . . 1 . . . . . . . . . . . . . 1
18 1 1 1 1 1 . 1 1 1 1 1 . 1 1 1 1 . . 1 1 1
19 1 1 1 . 1 . 1 . . 1 1 . . 1 1 . . 1 . 1 .
20 1 1 . . . 1 . 1 . . 1 1 . 1 1 1 1 1 . . 1
21 . 1 1 1 . 1 1 1 . . . 1 . 1 . . 1 1 . 1 .
>
> krack_reports_to <- delete.edges(krack_full, E(krack_full)[E(krack_full)$reports_to_tie==0])
> summary(krack_reports_to)
IGRAPH 9c7cb3e DN-- 21 20 --
+ attr: name (v/c), advice_tie (e/n), friendship_tie (e/n),
| reports_to_tie (e/n)
> krack_reports_to[]
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . . . . . . . . . . . . . . . . . . .
2 . . . . . . 1 . . . . . . . . . . . . . .
3 . . . . . . . . . . . . . 1 . . . . . . .
4 . 1 . . . . . . . . . . . . . . . . . . .
5 . . . . . . . . . . . . . 1 . . . . . . .
6 . . . . . . . . . . . . . . . . . . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . . . . . . . . . . . . . . . . . . 1
9 . . . . . . . . . . . . . 1 . . . . . . .
10 . . . . . . . . . . . . . . . . . 1 . . .
11 . . . . . . . . . . . . . . . . . 1 . . .
12 . . . . . . . . . . . . . . . . . . . . 1
13 . . . . . . . . . . . . . 1 . . . . . . .
14 . . . . . . 1 . . . . . . . . . . . . . .
15 . . . . . . . . . . . . . 1 . . . . . . .
16 . 1 . . . . . . . . . . . . . . . . . . .
17 . . . . . . . . . . . . . . . . . . . . 1
18 . . . . . . 1 . . . . . . . . . . . . . .
19 . . . . . . . . . . . . . 1 . . . . . . .
20 . . . . . . . . . . . . . 1 . . . . . . .
21 . . . . . . 1 . . . . . . . . . . . . . .
>
Visualization of the three (friend, advice, reports_to)
Note that reports to graph looks extremely formal.
par(mfrow = c(1,3)) krack_friend_layout <- layout.fruchterman.reingold(krack_friend) plot(krack_friend, layout=krack_friend_layout, main = "friend", edge.arrow.size=.5) krack_advice_layout <- layout.fruchterman.reingold(krack_advice) plot(krack_advice, layout=krack_advice_layout, main = "advice", edge.arrow.size=.5) krack_reports_to_layout <- layout.fruchterman.reingold(krack_reports_to) plot(krack_reports_to, layout=krack_reports_to_layout, main = "reports to", edge.arrow.size=.5) par(mfrow = c(1,1))
Two data sets (friend and advice), for friend
# We'll use the "task" and "social" sub-graphs together as the # basis for our structural equivalence methods. First, we'll use # the task graph to generate an adjacency matrix. # # This matrix represents task interactions directed FROM the # row individual TO the column individual. krack_friend_matrix_row_to_col <- get.adjacency(krack_friend, attr='friendship_tie') krack_friend_matrix_row_to_col # To operate on a binary graph, simply leave off the "attr" # parameter: krack_friend_matrix_row_to_col_bin <- get.adjacency(krack_friend) krack_friend_matrix_row_to_col_bin # For this lab, we'll use the valued graph. The next step is to # concatenate it with its transpose in order to capture both # incoming and outgoing task interactions. krack_friend_matrix_col_to_row <- t(as.matrix(krack_friend_matrix_row_to_col)) krack_friend_matrix_col_to_row krack_friend_matrix <- rbind(krack_friend_matrix_row_to_col, krack_friend_matrix_col_to_row) krack_friend_matrix
> krack_friend_matrix_row_to_col <- get.adjacency(krack_friend, attr='friendship_tie')
> krack_friend_matrix_row_to_col
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . 1 . . . 1 . . . . .
2 1 . . . . . . . . . . . . . . . . 1 . . 1
3 . . . . . . . . . . . . . 1 . . . . 1 . .
4 1 1 . . . . . 1 . . . 1 . . . 1 1 . . . .
5 . 1 . . . . . . 1 . 1 . . 1 . . 1 . 1 . 1
6 . 1 . . . . 1 . 1 . . 1 . . . . 1 . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . 1 . . . . . . . . . . . . . . . . .
9 . . . . . . . . . . . . . . . . . . . . .
10 . . 1 . 1 . . 1 1 . . 1 . . . 1 . . . 1 .
11 1 1 1 1 1 . . 1 1 . . 1 1 . 1 . 1 1 1 . .
12 1 . . 1 . . . . . . . . . . . . 1 . . . 1
13 . . . . 1 . . . . . 1 . . . . . . . . . .
14 . . . . . . 1 . . . . . . . 1 . . . . . .
15 1 . 1 . 1 1 . . 1 . 1 . . 1 . . . . 1 . .
16 1 1 . . . . . . . . . . . . . . . . . . .
17 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 . . 1 1 1
18 . 1 . . . . . . . . . . . . . . . . . . .
19 1 1 1 . 1 . . . . . 1 1 . 1 1 . . . . 1 .
20 . . . . . . . . . . 1 . . . . . . 1 . . .
21 . 1 . . . . . . . . . 1 . . . . 1 1 . . .
>
> # To operate on a binary graph, simply leave off the "attr"
> # parameter:
> krack_friend_matrix_row_to_col_bin <- get.adjacency(krack_friend)
> krack_friend_matrix_row_to_col_bin
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . 1 . . . 1 . . . . .
2 1 . . . . . . . . . . . . . . . . 1 . . 1
3 . . . . . . . . . . . . . 1 . . . . 1 . .
4 1 1 . . . . . 1 . . . 1 . . . 1 1 . . . .
5 . 1 . . . . . . 1 . 1 . . 1 . . 1 . 1 . 1
6 . 1 . . . . 1 . 1 . . 1 . . . . 1 . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . 1 . . . . . . . . . . . . . . . . .
9 . . . . . . . . . . . . . . . . . . . . .
10 . . 1 . 1 . . 1 1 . . 1 . . . 1 . . . 1 .
11 1 1 1 1 1 . . 1 1 . . 1 1 . 1 . 1 1 1 . .
12 1 . . 1 . . . . . . . . . . . . 1 . . . 1
13 . . . . 1 . . . . . 1 . . . . . . . . . .
14 . . . . . . 1 . . . . . . . 1 . . . . . .
15 1 . 1 . 1 1 . . 1 . 1 . . 1 . . . . 1 . .
16 1 1 . . . . . . . . . . . . . . . . . . .
17 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 . . 1 1 1
18 . 1 . . . . . . . . . . . . . . . . . . .
19 1 1 1 . 1 . . . . . 1 1 . 1 1 . . . . 1 .
20 . . . . . . . . . . 1 . . . . . . 1 . . .
21 . 1 . . . . . . . . . 1 . . . . 1 1 . . .
>
> # For this lab, we'll use the valued graph. The next step is to
> # concatenate it with its transpose in order to capture both
> # incoming and outgoing task interactions.
> krack_friend_matrix_col_to_row <- t(as.matrix(krack_friend_matrix_row_to_col))
> krack_friend_matrix_col_to_row
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1 0 1 0 1 0 0 0 0 0 0 1 1 0 0 1 1 1 0 1 0 0
2 1 0 0 1 1 1 0 0 0 0 1 0 0 0 0 1 1 1 1 0 1
3 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 1 0 1 0 0
4 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 0 0
5 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 0 1 0 1 0 0
6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0
7 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0
8 1 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0
9 0 0 0 0 1 1 0 0 0 1 1 0 0 0 1 0 1 0 0 0 0
10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
11 0 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 1 0 1 1 0
12 1 0 0 1 0 1 0 0 0 1 1 0 0 0 0 0 1 0 1 0 1
13 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
14 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0
15 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 0
16 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0
17 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1
18 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1
19 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0
20 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0
21 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0
>
> krack_friend_matrix <- rbind(krack_friend_matrix_row_to_col, krack_friend_matrix_col_to_row)
> krack_friend_matrix
42 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . 1 . . . 1 . . . . .
2 1 . . . . . . . . . . . . . . . . 1 . . 1
3 . . . . . . . . . . . . . 1 . . . . 1 . .
4 1 1 . . . . . 1 . . . 1 . . . 1 1 . . . .
5 . 1 . . . . . . 1 . 1 . . 1 . . 1 . 1 . 1
6 . 1 . . . . 1 . 1 . . 1 . . . . 1 . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . 1 . . . . . . . . . . . . . . . . .
9 . . . . . . . . . . . . . . . . . . . . .
10 . . 1 . 1 . . 1 1 . . 1 . . . 1 . . . 1 .
11 1 1 1 1 1 . . 1 1 . . 1 1 . 1 . 1 1 1 . .
12 1 . . 1 . . . . . . . . . . . . 1 . . . 1
13 . . . . 1 . . . . . 1 . . . . . . . . . .
14 . . . . . . 1 . . . . . . . 1 . . . . . .
15 1 . 1 . 1 1 . . 1 . 1 . . 1 . . . . 1 . .
16 1 1 . . . . . . . . . . . . . . . . . . .
17 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 . . 1 1 1
18 . 1 . . . . . . . . . . . . . . . . . . .
19 1 1 1 . 1 . . . . . 1 1 . 1 1 . . . . 1 .
20 . . . . . . . . . . 1 . . . . . . 1 . . .
21 . 1 . . . . . . . . . 1 . . . . 1 1 . . .
1 . 1 . 1 . . . . . . 1 1 . . 1 1 1 . 1 . .
2 1 . . 1 1 1 . . . . 1 . . . . 1 1 1 1 . 1
3 . . . . . . . . . 1 1 . . . 1 . 1 . 1 . .
4 1 . . . . . . 1 . . 1 1 . . . . 1 . . . .
5 . . . . . . . . . 1 1 . 1 . 1 . 1 . 1 . .
6 . . . . . . . . . . . . . . 1 . 1 . . . .
7 . . . . . 1 . . . . . . . 1 . . 1 . . . .
8 1 . . 1 . . . . . 1 1 . . . . . 1 . . . .
9 . . . . 1 1 . . . 1 1 . . . 1 . 1 . . . .
10 . . . . . . . . . . . . . . . . 1 . . . .
11 . . . . 1 . . . . . . . 1 . 1 . 1 . 1 1 .
12 1 . . 1 . 1 . . . 1 1 . . . . . 1 . 1 . 1
13 . . . . . . . . . . 1 . . . . . . . . . .
14 . . 1 . 1 . . . . . . . . . 1 . 1 . 1 . .
15 . . . . . . . . . . 1 . . 1 . . 1 . 1 . .
16 1 . . 1 . . . . . 1 . . . . . . 1 . . . .
17 . . . 1 1 1 . . . . 1 1 . . . . . . . . 1
18 . 1 . . . . . . . . 1 . . . . . . . . 1 1
19 . . 1 . 1 . . . . . 1 . . . 1 . 1 . . . .
20 . . . . . . . . . 1 . . . . . . 1 . 1 . .
21 . 1 . . 1 1 . . . . . 1 . . . . 1 . . . .
>
>
for advice matrix
# Next, we'll use the same procedure to add social-interaction # information. krack_advice_matrix_row_to_col <- get.adjacency(krack_advice, attr='advice_tie') krack_advice_matrix_row_to_col krack_advice_matrix_row_to_col_bin <- get.adjacency(krack_advice) krack_advice_matrix_row_to_col_bin krack_advice_matrix_col_to_row <- t(as.matrix(krack_advice_matrix_row_to_col)) krack_advice_matrix_col_to_row krack_advice_matrix <- rbind(krack_advice_matrix_row_to_col, krack_advice_matrix_col_to_row) krack_advice_matrix
> krack_advice_matrix_row_to_col <- get.adjacency(krack_advice, attr='advice_tie')
> krack_advice_matrix_row_to_col
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . . . . . 1 . 1 . . 1
2 . . . . . 1 1 . . . . . . . . . . . . . 1
3 1 1 . 1 . 1 1 1 1 1 1 1 . 1 . . 1 1 . 1 1
4 1 1 . . . 1 . 1 . 1 1 1 . . . 1 1 1 . 1 1
5 1 1 . . . 1 1 1 . 1 1 . 1 1 . 1 1 1 1 1 1
6 . . . . . . . . . . . . . . . . . . . . 1
7 . 1 . . . 1 . . . . 1 1 . 1 . . 1 1 . . 1
8 . 1 . 1 . 1 1 . . 1 1 . . . . . . 1 . . 1
9 1 1 . . . 1 1 1 . 1 1 1 . 1 . 1 1 1 . . 1
10 1 1 1 1 1 . . 1 . . 1 . 1 . 1 1 1 1 1 1 .
11 1 1 . . . . 1 . . . . . . . . . . . . . .
12 . . . . . . 1 . . . . . . . . . . . . . 1
13 1 1 . . 1 . . . 1 . . . . 1 . . . 1 . . .
14 . 1 . . . . 1 . . . . . . . . . . 1 . . 1
15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1
16 1 1 . . . . . . . 1 . . . . . . . 1 . . .
17 1 1 . 1 . . 1 . . . . . . . . . . . . . 1
18 1 1 1 1 1 . 1 1 1 1 1 . 1 1 1 1 . . 1 1 1
19 1 1 1 . 1 . 1 . . 1 1 . . 1 1 . . 1 . 1 .
20 1 1 . . . 1 . 1 . . 1 1 . 1 1 1 1 1 . . 1
21 . 1 1 1 . 1 1 1 . . . 1 . 1 . . 1 1 . 1 .
>
> krack_advice_matrix_row_to_col_bin <- get.adjacency(krack_advice)
> krack_advice_matrix_row_to_col_bin
21 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . . . . . 1 . 1 . . 1
2 . . . . . 1 1 . . . . . . . . . . . . . 1
3 1 1 . 1 . 1 1 1 1 1 1 1 . 1 . . 1 1 . 1 1
4 1 1 . . . 1 . 1 . 1 1 1 . . . 1 1 1 . 1 1
5 1 1 . . . 1 1 1 . 1 1 . 1 1 . 1 1 1 1 1 1
6 . . . . . . . . . . . . . . . . . . . . 1
7 . 1 . . . 1 . . . . 1 1 . 1 . . 1 1 . . 1
8 . 1 . 1 . 1 1 . . 1 1 . . . . . . 1 . . 1
9 1 1 . . . 1 1 1 . 1 1 1 . 1 . 1 1 1 . . 1
10 1 1 1 1 1 . . 1 . . 1 . 1 . 1 1 1 1 1 1 .
11 1 1 . . . . 1 . . . . . . . . . . . . . .
12 . . . . . . 1 . . . . . . . . . . . . . 1
13 1 1 . . 1 . . . 1 . . . . 1 . . . 1 . . .
14 . 1 . . . . 1 . . . . . . . . . . 1 . . 1
15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1
16 1 1 . . . . . . . 1 . . . . . . . 1 . . .
17 1 1 . 1 . . 1 . . . . . . . . . . . . . 1
18 1 1 1 1 1 . 1 1 1 1 1 . 1 1 1 1 . . 1 1 1
19 1 1 1 . 1 . 1 . . 1 1 . . 1 1 . . 1 . 1 .
20 1 1 . . . 1 . 1 . . 1 1 . 1 1 1 1 1 . . 1
21 . 1 1 1 . 1 1 1 . . . 1 . 1 . . 1 1 . 1 .
>
> krack_advice_matrix_col_to_row <- t(as.matrix(krack_advice_matrix_row_to_col))
> krack_advice_matrix_col_to_row
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1 0 0 1 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0
2 1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1
3 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 1 0 1
4 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 1 0 0 1
5 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 1 1 0 0
6 0 1 1 1 1 0 1 1 1 0 0 0 0 0 1 0 0 0 0 1 1
7 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 1 1 1 0 1
8 1 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 1
9 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0
10 0 0 1 1 1 0 0 1 1 0 0 0 0 0 1 1 0 1 1 0 0
11 0 0 1 1 1 0 1 1 1 1 0 0 0 0 1 0 0 1 1 1 0
12 0 0 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1
13 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0
14 0 0 1 0 1 0 1 0 1 0 0 0 1 0 1 0 0 1 1 1 1
15 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0
16 1 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 1 0 1 0
17 0 0 1 1 1 0 1 0 1 1 0 0 0 0 1 0 0 0 0 1 1
18 1 0 1 1 1 0 1 1 1 1 0 0 1 1 1 1 0 0 1 1 1
19 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0
20 0 0 1 1 1 0 0 0 0 1 0 0 0 0 1 0 0 1 1 0 1
21 1 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 1 1 0 1 0
>
> krack_advice_matrix <- rbind(krack_advice_matrix_row_to_col, krack_advice_matrix_col_to_row)
> krack_advice_matrix
42 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . . . . . 1 . 1 . . 1
2 . . . . . 1 1 . . . . . . . . . . . . . 1
3 1 1 . 1 . 1 1 1 1 1 1 1 . 1 . . 1 1 . 1 1
4 1 1 . . . 1 . 1 . 1 1 1 . . . 1 1 1 . 1 1
5 1 1 . . . 1 1 1 . 1 1 . 1 1 . 1 1 1 1 1 1
6 . . . . . . . . . . . . . . . . . . . . 1
7 . 1 . . . 1 . . . . 1 1 . 1 . . 1 1 . . 1
8 . 1 . 1 . 1 1 . . 1 1 . . . . . . 1 . . 1
9 1 1 . . . 1 1 1 . 1 1 1 . 1 . 1 1 1 . . 1
10 1 1 1 1 1 . . 1 . . 1 . 1 . 1 1 1 1 1 1 .
11 1 1 . . . . 1 . . . . . . . . . . . . . .
12 . . . . . . 1 . . . . . . . . . . . . . 1
13 1 1 . . 1 . . . 1 . . . . 1 . . . 1 . . .
14 . 1 . . . . 1 . . . . . . . . . . 1 . . 1
15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 1 1 1
16 1 1 . . . . . . . 1 . . . . . . . 1 . . .
17 1 1 . 1 . . 1 . . . . . . . . . . . . . 1
18 1 1 1 1 1 . 1 1 1 1 1 . 1 1 1 1 . . 1 1 1
19 1 1 1 . 1 . 1 . . 1 1 . . 1 1 . . 1 . 1 .
20 1 1 . . . 1 . 1 . . 1 1 . 1 1 1 1 1 . . 1
21 . 1 1 1 . 1 1 1 . . . 1 . 1 . . 1 1 . 1 .
1 . . 1 1 1 . . . 1 1 1 . 1 . 1 1 1 1 1 1 .
2 1 . 1 1 1 . 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1
3 . . . . . . . . . 1 . . . . 1 . . 1 1 . 1
4 1 . 1 . . . . 1 . 1 . . . . 1 . 1 1 . . 1
5 . . . . . . . . . 1 . . 1 . 1 . . 1 1 . .
6 . 1 1 1 1 . 1 1 1 . . . . . 1 . . . . 1 1
7 . 1 1 . 1 . . 1 1 . 1 1 . 1 1 . 1 1 1 . 1
8 1 . 1 1 1 . . . 1 1 . . . . 1 . . 1 . 1 1
9 . . 1 . . . . . . . . . 1 . 1 . . 1 . . .
10 . . 1 1 1 . . 1 1 . . . . . 1 1 . 1 1 . .
11 . . 1 1 1 . 1 1 1 1 . . . . 1 . . 1 1 1 .
12 . . 1 1 . . 1 . 1 . . . . . 1 . . . . 1 1
13 . . . . 1 . . . . 1 . . . . 1 . . 1 . . .
14 . . 1 . 1 . 1 . 1 . . . 1 . 1 . . 1 1 1 1
15 . . . . . . . . . 1 . . . . . . . 1 1 1 .
16 1 . . 1 1 . . . 1 1 . . . . 1 . . 1 . 1 .
17 . . 1 1 1 . 1 . 1 1 . . . . 1 . . . . 1 1
18 1 . 1 1 1 . 1 1 1 1 . . 1 1 1 1 . . 1 1 1
19 . . . . 1 . . . . 1 . . . . 1 . . 1 . . .
20 . . 1 1 1 . . . . 1 . . . . 1 . . 1 1 . 1
21 1 1 1 1 1 1 1 1 1 . . 1 . 1 1 . 1 1 . 1 .
>
combining the two (friend and advice)
# combine the two with rbind function krack_friend_advice_matrix <- rbind(krack_friend_matrix, krack_advice_matrix) krack_friend_advice_matrix
> # combine the two with rbind function
> krack_friend_advice_matrix <- rbind(krack_friend_matrix, krack_advice_matrix)
> krack_friend_advice_matrix
84 x 21 sparse Matrix of class "dgCMatrix"
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
1 . 1 . 1 . . . 1 . . . 1 . . . 1 . . . . .
2 1 . . . . . . . . . . . . . . . . 1 . . 1
3 . . . . . . . . . . . . . 1 . . . . 1 . .
4 1 1 . . . . . 1 . . . 1 . . . 1 1 . . . .
5 . 1 . . . . . . 1 . 1 . . 1 . . 1 . 1 . 1
6 . 1 . . . . 1 . 1 . . 1 . . . . 1 . . . 1
7 . . . . . . . . . . . . . . . . . . . . .
8 . . . 1 . . . . . . . . . . . . . . . . .
9 . . . . . . . . . . . . . . . . . . . . .
10 . . 1 . 1 . . 1 1 . . 1 . . . 1 . . . 1 .
11 1 1 1 1 1 . . 1 1 . . 1 1 . 1 . 1 1 1 . .
12 1 . . 1 . . . . . . . . . . . . 1 . . . 1
13 . . . . 1 . . . . . 1 . . . . . . . . . .
14 . . . . . . 1 . . . . . . . 1 . . . . . .
15 1 . 1 . 1 1 . . 1 . 1 . . 1 . . . . 1 . .
16 1 1 . . . . . . . . . . . . . . . . . . .
17 1 1 1 1 1 1 1 1 1 1 1 1 . 1 1 1 . . 1 1 1
18 . 1 . . . . . . . . . . . . . . . . . . .
19 1 1 1 . 1 . . . . . 1 1 . 1 1 . . . . 1 .
20 . . . . . . . . . . 1 . . . . . . 1 . . .
21 . 1 . . . . . . . . . 1 . . . . 1 1 . . .
1 . 1 . 1 . . . . . . 1 1 . . 1 1 1 . 1 . .
2 1 . . 1 1 1 . . . . 1 . . . . 1 1 1 1 . 1
3 . . . . . . . . . 1 1 . . . 1 . 1 . 1 . .
..............................
........suppressing 37 rows in show(); maybe adjust 'options(max.print= *, width = *)'
..............................
[[ suppressing 21 column names ‘1’, ‘2’, ‘3’ ... ]]
20 1 1 . . . 1 . 1 . . 1 1 . 1 1 1 1 1 . . 1
21 . 1 1 1 . 1 1 1 . . . 1 . 1 . . 1 1 . 1 .
1 . . 1 1 1 . . . 1 1 1 . 1 . 1 1 1 1 1 1 .
2 1 . 1 1 1 . 1 1 1 1 1 . 1 1 1 1 1 1 1 1 1
3 . . . . . . . . . 1 . . . . 1 . . 1 1 . 1
4 1 . 1 . . . . 1 . 1 . . . . 1 . 1 1 . . 1
5 . . . . . . . . . 1 . . 1 . 1 . . 1 1 . .
6 . 1 1 1 1 . 1 1 1 . . . . . 1 . . . . 1 1
7 . 1 1 . 1 . . 1 1 . 1 1 . 1 1 . 1 1 1 . 1
8 1 . 1 1 1 . . . 1 1 . . . . 1 . . 1 . 1 1
9 . . 1 . . . . . . . . . 1 . 1 . . 1 . . .
10 . . 1 1 1 . . 1 1 . . . . . 1 1 . 1 1 . .
11 . . 1 1 1 . 1 1 1 1 . . . . 1 . . 1 1 1 .
12 . . 1 1 . . 1 . 1 . . . . . 1 . . . . 1 1
13 . . . . 1 . . . . 1 . . . . 1 . . 1 . . .
14 . . 1 . 1 . 1 . 1 . . . 1 . 1 . . 1 1 1 1
15 . . . . . . . . . 1 . . . . . . . 1 1 1 .
16 1 . . 1 1 . . . 1 1 . . . . 1 . . 1 . 1 .
17 . . 1 1 1 . 1 . 1 1 . . . . 1 . . . . 1 1
18 1 . 1 1 1 . 1 1 1 1 . . 1 1 1 1 . . 1 1 1
19 . . . . 1 . . . . 1 . . . . 1 . . 1 . . .
20 . . 1 1 1 . . . . 1 . . . . 1 . . 1 1 . 1
21 1 1 1 1 1 1 1 1 1 . . 1 . 1 1 . 1 1 . 1 .
>
correlation matrix out of the combined matrix (friend and advice)
# Now we have a single 4n x n matrix that represents both in- and # out-directed task and social communication. From this, we can # generate an n x n correlation matrix that shows the degree of # structural equivalence of each actor in the network. krack_friend_advice_cors <- cor(as.matrix(krack_friend_advice_matrix)) krack_friend_advice_cors round(krack_friend_advice_cors, 2)
> krack_friend_advice_cors <- cor(as.matrix(krack_friend_advice_matrix))
> krack_friend_advice_cors
1 2 3 4 5 6 7 8 9 10 11 12 13
1 1.000000000 0.302038699 0.142475069 0.263688413 0.12190217 0.22043317 0.15504342 0.3721042 0.178017791 0.26368841 0.222292198 0.16984156 0.13878769
2 0.302038699 1.000000000 0.003709433 0.072998946 -0.06739665 0.24983348 0.28377705 0.3911521 0.091946467 -0.12804733 0.180906807 0.53210643 -0.01756295
3 0.142475069 0.003709433 1.000000000 0.371663052 0.64682882 -0.06745749 0.29825135 0.4111032 0.606358624 0.10753703 0.020504660 0.07358513 0.33980899
4 0.263688413 0.072998946 0.371663052 1.000000000 0.29406817 0.11723687 0.28085601 0.3354669 0.415605936 0.23311016 0.041494282 0.07121813 0.15022842
5 0.121902173 -0.067396653 0.646828819 0.294068170 1.00000000 0.03121311 0.08479117 0.1927072 0.544696475 0.14252384 0.101604278 0.04222003 0.26236436
6 0.220433168 0.249833476 -0.067457487 0.117236869 0.03121311 1.00000000 0.22496064 0.2249606 -0.012914768 0.11723687 0.380799884 0.41072005 -0.07399336
7 0.155043418 0.283777046 0.298251347 0.280856008 0.08479117 0.22496064 1.00000000 0.3000000 0.379912583 0.17163423 -0.023124865 0.06085806 0.16654022
8 0.372104204 0.391152144 0.411103208 0.335466899 0.19270720 0.22496064 0.30000000 1.0000000 0.379912583 0.11702334 0.138749187 0.48686450 0.23940157
9 0.178017791 0.091946467 0.606358624 0.415605936 0.54469647 -0.01291477 0.37991258 0.3799126 1.000000000 0.13897441 -0.001952317 0.13872446 0.25396166
10 0.263688413 -0.128047331 0.107537025 0.233110164 0.14252384 0.11723687 0.17163423 0.1170233 0.138974410 1.00000000 0.193038615 -0.15667990 0.21844024
11 0.222292198 0.180906807 0.020504660 0.041494282 0.10160428 0.38079988 -0.02312486 0.1387492 -0.001952317 0.19303861 1.000000000 0.21110017 0.12757166
12 0.169841555 0.532106432 0.073585131 0.071218135 0.04222003 0.41072005 0.06085806 0.4868645 0.138724461 -0.15667990 0.211100165 1.00000000 -0.09501858
13 0.138787686 -0.017562946 0.339808989 0.150228419 0.26236436 -0.07399336 0.16654022 0.2394016 0.253961660 0.21844024 0.127571663 -0.09501858 1.00000000
14 0.339683110 0.364072822 0.250189445 0.014243627 0.15480679 0.41072005 0.30429031 0.3651484 0.323690409 0.07121813 0.379980298 0.30158730 0.13302601
15 -0.035383657 -0.175035011 0.588681048 0.185167150 0.53478709 -0.23821763 0.09128709 0.1445379 0.331397324 0.28487254 -0.007036672 -0.11111111 0.36107060
16 0.307254934 0.278652218 0.199680766 0.322096134 0.17397419 0.20309228 0.11927107 0.6330542 0.199840105 0.14172230 0.292785836 0.30151134 0.33806031
17 0.173557880 0.127622576 -0.062188509 -0.001180159 -0.09445006 0.30899515 -0.15127226 0.2193448 -0.075349861 0.04838652 0.346316890 0.35903931 0.14013559
18 0.192817919 0.196581411 0.210887090 0.116546075 0.17009876 0.15080266 0.07583160 0.2881601 0.154290226 0.31532517 0.022796741 0.09691425 0.21706113
19 -0.002455291 -0.139676400 0.304451926 0.171112069 0.28747396 -0.03348760 -0.01583615 0.1504434 0.284105572 0.27489123 0.236204715 -0.13010726 0.52005367
20 0.240002173 0.152825173 0.555533353 0.365508495 0.43603231 0.08372380 0.45286283 0.3952257 0.534566198 0.31154942 0.116148344 0.10523044 0.36938598
21 0.182323225 0.188581614 0.090482786 0.254376526 -0.03708228 0.29340150 0.42761799 0.2138090 0.239173474 0.15429396 0.160689880 0.06970715 0.03894603
14 15 16 17 18 19 20 21
1 0.33968311 -0.035383657 0.30725493 0.173557880 0.19281792 -0.002455291 0.24000217 0.18232322
2 0.36407282 -0.175035011 0.27865222 0.127622576 0.19658141 -0.139676400 0.15282517 0.18858161
3 0.25018945 0.588681048 0.19968077 -0.062188509 0.21088709 0.304451926 0.55553335 0.09048279
4 0.01424363 0.185167150 0.32209613 -0.001180159 0.11654608 0.171112069 0.36550849 0.25437653
5 0.15480679 0.534787086 0.17397419 -0.094450061 0.17009876 0.287473956 0.43603231 -0.03708228
6 0.41072005 -0.238217628 0.20309228 0.308995148 0.15080266 -0.033487601 0.08372380 0.29340150
7 0.30429031 0.091287093 0.11927107 -0.151272255 0.07583160 -0.015836152 0.45286283 0.42761799
8 0.36514837 0.144537897 0.63305416 0.219344770 0.28816007 0.150443441 0.39522575 0.21380899
9 0.32369041 0.331397324 0.19984011 -0.075349861 0.15429023 0.284105572 0.53456620 0.23917347
10 0.07121813 0.284872539 0.14172230 0.048386516 0.31532517 0.274891231 0.31154942 0.15429396
11 0.37998030 -0.007036672 0.29278584 0.346316890 0.02279674 0.236204715 0.11614834 0.16068988
12 0.30158730 -0.111111111 0.30151134 0.359039315 0.09691425 -0.130107262 0.10523044 0.06970715
13 0.13302601 0.361070596 0.33806031 0.140135587 0.21706113 0.520053669 0.36938598 0.03894603
14 1.00000000 0.000000000 0.23450882 0.193328862 0.15229382 0.216845437 0.28562549 0.18123858
15 0.00000000 1.000000000 0.07537784 -0.013809204 0.20075094 0.332496337 0.33072425 -0.04879500
16 0.23450882 0.075377836 1.00000000 0.166545272 0.17949886 0.292036738 0.29461875 0.20597146
17 0.19332886 -0.013809204 0.16654527 1.000000000 0.01261834 0.195238985 -0.06850558 -0.04042921
18 0.15229382 0.200750938 0.17949886 0.012618339 1.00000000 0.112282344 0.20916981 0.17429489
19 0.21684544 0.332496337 0.29203674 0.195238985 0.11228234 1.000000000 0.18450582 0.04655629
20 0.28562549 0.330724252 0.29461875 -0.068505582 0.20916981 0.184505825 1.00000000 0.18925110
21 0.18123858 -0.048795004 0.20597146 -0.040429211 0.17429489 0.046556285 0.18925110 1.00000000
> round(krack_friend_advice_cors, 2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1 1.00 0.30 0.14 0.26 0.12 0.22 0.16 0.37 0.18 0.26 0.22 0.17 0.14 0.34 -0.04 0.31 0.17 0.19 0.00 0.24 0.18
2 0.30 1.00 0.00 0.07 -0.07 0.25 0.28 0.39 0.09 -0.13 0.18 0.53 -0.02 0.36 -0.18 0.28 0.13 0.20 -0.14 0.15 0.19
3 0.14 0.00 1.00 0.37 0.65 -0.07 0.30 0.41 0.61 0.11 0.02 0.07 0.34 0.25 0.59 0.20 -0.06 0.21 0.30 0.56 0.09
4 0.26 0.07 0.37 1.00 0.29 0.12 0.28 0.34 0.42 0.23 0.04 0.07 0.15 0.01 0.19 0.32 0.00 0.12 0.17 0.37 0.25
5 0.12 -0.07 0.65 0.29 1.00 0.03 0.08 0.19 0.54 0.14 0.10 0.04 0.26 0.15 0.53 0.17 -0.09 0.17 0.29 0.44 -0.04
6 0.22 0.25 -0.07 0.12 0.03 1.00 0.22 0.22 -0.01 0.12 0.38 0.41 -0.07 0.41 -0.24 0.20 0.31 0.15 -0.03 0.08 0.29
7 0.16 0.28 0.30 0.28 0.08 0.22 1.00 0.30 0.38 0.17 -0.02 0.06 0.17 0.30 0.09 0.12 -0.15 0.08 -0.02 0.45 0.43
8 0.37 0.39 0.41 0.34 0.19 0.22 0.30 1.00 0.38 0.12 0.14 0.49 0.24 0.37 0.14 0.63 0.22 0.29 0.15 0.40 0.21
9 0.18 0.09 0.61 0.42 0.54 -0.01 0.38 0.38 1.00 0.14 0.00 0.14 0.25 0.32 0.33 0.20 -0.08 0.15 0.28 0.53 0.24
10 0.26 -0.13 0.11 0.23 0.14 0.12 0.17 0.12 0.14 1.00 0.19 -0.16 0.22 0.07 0.28 0.14 0.05 0.32 0.27 0.31 0.15
11 0.22 0.18 0.02 0.04 0.10 0.38 -0.02 0.14 0.00 0.19 1.00 0.21 0.13 0.38 -0.01 0.29 0.35 0.02 0.24 0.12 0.16
12 0.17 0.53 0.07 0.07 0.04 0.41 0.06 0.49 0.14 -0.16 0.21 1.00 -0.10 0.30 -0.11 0.30 0.36 0.10 -0.13 0.11 0.07
13 0.14 -0.02 0.34 0.15 0.26 -0.07 0.17 0.24 0.25 0.22 0.13 -0.10 1.00 0.13 0.36 0.34 0.14 0.22 0.52 0.37 0.04
14 0.34 0.36 0.25 0.01 0.15 0.41 0.30 0.37 0.32 0.07 0.38 0.30 0.13 1.00 0.00 0.23 0.19 0.15 0.22 0.29 0.18
15 -0.04 -0.18 0.59 0.19 0.53 -0.24 0.09 0.14 0.33 0.28 -0.01 -0.11 0.36 0.00 1.00 0.08 -0.01 0.20 0.33 0.33 -0.05
16 0.31 0.28 0.20 0.32 0.17 0.20 0.12 0.63 0.20 0.14 0.29 0.30 0.34 0.23 0.08 1.00 0.17 0.18 0.29 0.29 0.21
17 0.17 0.13 -0.06 0.00 -0.09 0.31 -0.15 0.22 -0.08 0.05 0.35 0.36 0.14 0.19 -0.01 0.17 1.00 0.01 0.20 -0.07 -0.04
18 0.19 0.20 0.21 0.12 0.17 0.15 0.08 0.29 0.15 0.32 0.02 0.10 0.22 0.15 0.20 0.18 0.01 1.00 0.11 0.21 0.17
19 0.00 -0.14 0.30 0.17 0.29 -0.03 -0.02 0.15 0.28 0.27 0.24 -0.13 0.52 0.22 0.33 0.29 0.20 0.11 1.00 0.18 0.05
20 0.24 0.15 0.56 0.37 0.44 0.08 0.45 0.40 0.53 0.31 0.12 0.11 0.37 0.29 0.33 0.29 -0.07 0.21 0.18 1.00 0.19
21 0.18 0.19 0.09 0.25 -0.04 0.29 0.43 0.21 0.24 0.15 0.16 0.07 0.04 0.18 -0.05 0.21 -0.04 0.17 0.05 0.19 1.00
>
Clustering with NetCluster
# To use correlation values in hierarchical NetCluster, they must # first be coerced into a "dissimilarity structure" using dist(). # We subtract the values from 1 so that they are all greater than # or equal to 0; thus, highly dissimilar (i.e., negatively # correlated) actors have higher values. dissimilarity <- 1 - krack_friend_advice_cors krack_friend_advice_dist <- as.dist(dissimilarity) krack_friend_advice_dist round(krack_friend_advice_dist, 2)
> dissimilarity <- 1 - krack_friend_advice_cors
> krack_friend_advice_dist <- as.dist(dissimilarity)
> krack_friend_advice_dist
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2 0.6979613
3 0.8575249 0.9962906
4 0.7363116 0.9270011 0.6283369
5 0.8780978 1.0673967 0.3531712 0.7059318
6 0.7795668 0.7501665 1.0674575 0.8827631 0.9687869
7 0.8449566 0.7162230 0.7017487 0.7191440 0.9152088 0.7750394
8 0.6278958 0.6088479 0.5888968 0.6645331 0.8072928 0.7750394 0.7000000
9 0.8219822 0.9080535 0.3936414 0.5843941 0.4553035 1.0129148 0.6200874 0.6200874
10 0.7363116 1.1280473 0.8924630 0.7668898 0.8574762 0.8827631 0.8283658 0.8829767 0.8610256
11 0.7777078 0.8190932 0.9794953 0.9585057 0.8983957 0.6192001 1.0231249 0.8612508 1.0019523 0.8069614
12 0.8301584 0.4678936 0.9264149 0.9287819 0.9577800 0.5892800 0.9391419 0.5131355 0.8612755 1.1566799 0.7888998
13 0.8612123 1.0175629 0.6601910 0.8497716 0.7376356 1.0739934 0.8334598 0.7605984 0.7460383 0.7815598 0.8724283 1.0950186
14 0.6603169 0.6359272 0.7498106 0.9857564 0.8451932 0.5892800 0.6957097 0.6348516 0.6763096 0.9287819 0.6200197 0.6984127 0.8669740
15 1.0353837 1.1750350 0.4113190 0.8148328 0.4652129 1.2382176 0.9087129 0.8554621 0.6686027 0.7151275 1.0070367 1.1111111 0.6389294 1.0000000
16 0.6927451 0.7213478 0.8003192 0.6779039 0.8260258 0.7969077 0.8807289 0.3669458 0.8001599 0.8582777 0.7072142 0.6984887 0.6619397 0.7654912 0.9246222
17 0.8264421 0.8723774 1.0621885 1.0011802 1.0944501 0.6910049 1.1512723 0.7806552 1.0753499 0.9516135 0.6536831 0.6409607 0.8598644 0.8066711 1.0138092 0.8334547
18 0.8071821 0.8034186 0.7891129 0.8834539 0.8299012 0.8491973 0.9241684 0.7118399 0.8457098 0.6846748 0.9772033 0.9030858 0.7829389 0.8477062 0.7992491 0.8205011
19 1.0024553 1.1396764 0.6955481 0.8288879 0.7125260 1.0334876 1.0158362 0.8495566 0.7158944 0.7251088 0.7637953 1.1301073 0.4799463 0.7831546 0.6675037 0.7079633
20 0.7599978 0.8471748 0.4444666 0.6344915 0.5639677 0.9162762 0.5471372 0.6047743 0.4654338 0.6884506 0.8838517 0.8947696 0.6306140 0.7143745 0.6692757 0.7053813
21 0.8176768 0.8114184 0.9095172 0.7456235 1.0370823 0.7065985 0.5723820 0.7861910 0.7608265 0.8457060 0.8393101 0.9302929 0.9610540 0.8187614 1.0487950 0.7940285
17 18 19 20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 0.9873817
19 0.8047610 0.8877177
20 1.0685056 0.7908302 0.8154942
21 1.0404292 0.8257051 0.9534437 0.8107489
> round(krack_friend_advice_dist, 2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2 0.70
3 0.86 1.00
4 0.74 0.93 0.63
5 0.88 1.07 0.35 0.71
6 0.78 0.75 1.07 0.88 0.97
7 0.84 0.72 0.70 0.72 0.92 0.78
8 0.63 0.61 0.59 0.66 0.81 0.78 0.70
9 0.82 0.91 0.39 0.58 0.46 1.01 0.62 0.62
10 0.74 1.13 0.89 0.77 0.86 0.88 0.83 0.88 0.86
11 0.78 0.82 0.98 0.96 0.90 0.62 1.02 0.86 1.00 0.81
12 0.83 0.47 0.93 0.93 0.96 0.59 0.94 0.51 0.86 1.16 0.79
13 0.86 1.02 0.66 0.85 0.74 1.07 0.83 0.76 0.75 0.78 0.87 1.10
14 0.66 0.64 0.75 0.99 0.85 0.59 0.70 0.63 0.68 0.93 0.62 0.70 0.87
15 1.04 1.18 0.41 0.81 0.47 1.24 0.91 0.86 0.67 0.72 1.01 1.11 0.64 1.00
16 0.69 0.72 0.80 0.68 0.83 0.80 0.88 0.37 0.80 0.86 0.71 0.70 0.66 0.77 0.92
17 0.83 0.87 1.06 1.00 1.09 0.69 1.15 0.78 1.08 0.95 0.65 0.64 0.86 0.81 1.01 0.83
18 0.81 0.80 0.79 0.88 0.83 0.85 0.92 0.71 0.85 0.68 0.98 0.90 0.78 0.85 0.80 0.82 0.99
19 1.00 1.14 0.70 0.83 0.71 1.03 1.02 0.85 0.72 0.73 0.76 1.13 0.48 0.78 0.67 0.71 0.80 0.89
20 0.76 0.85 0.44 0.63 0.56 0.92 0.55 0.60 0.47 0.69 0.88 0.89 0.63 0.71 0.67 0.71 1.07 0.79 0.82
21 0.82 0.81 0.91 0.75 1.04 0.71 0.57 0.79 0.76 0.85 0.84 0.93 0.96 0.82 1.05 0.79 1.04 0.83 0.95 0.81
>
>
# Note that it is also possible to use dist() directly on the # matrix. However, since cor() looks at associations between # columns and dist() looks at associations between rows, it is # necessary to transpose the matrix first. # # A variety of distance metrics are available; Euclidean # is the default. krack_friend_advice_dist2 <- dist(t(krack_friend_advice_matrix)) krack_friend_advice_dist2
> krack_friend_advice_dist2 <- dist(t(as.matrix(krack_friend_advice_matrix)))
> krack_friend_advice_dist2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2 5.291503
3 5.744563 6.244998
4 5.385165 6.082763 4.898979
5 5.916080 6.557439 3.741657 5.291503
6 5.385165 5.385165 6.000000 5.656854 6.000000
7 5.656854 5.291503 5.000000 5.196152 5.916080 5.000000
8 4.898979 4.898979 4.582576 5.000000 5.567764 5.000000 4.898979
9 5.567764 5.916080 3.741657 4.690416 4.242641 5.656854 4.582576 4.582576
10 5.385165 6.708204 5.830952 5.477226 5.830952 5.656854 5.567764 5.744563 5.656854
11 5.567764 5.744563 6.164414 6.164414 6.000000 4.898979 6.244998 5.744563 6.164414 5.656854
12 5.567764 4.358899 5.656854 5.830952 6.000000 4.242641 5.567764 4.123106 5.291503 6.480741 5.477226
13 5.567764 6.082763 4.690416 5.477226 5.291503 5.291503 5.000000 4.795832 4.690416 5.291503 5.656854 5.477226
14 5.000000 5.000000 5.099020 6.000000 5.656854 4.242641 4.795832 4.582576 4.690416 5.830952 4.898979 4.690416 4.898979
15 6.480741 6.928203 4.123106 5.744563 4.358899 6.855655 6.000000 5.830952 5.196152 5.385165 6.403124 6.557439 5.196152 6.244998
16 5.099020 5.291503 5.196152 5.000000 5.567764 4.795832 5.291503 3.464102 5.000000 5.567764 5.196152 4.582576 4.123106 4.795832 6.000000
17 5.830952 6.000000 6.557439 6.403124 6.708204 5.385165 6.782330 5.656854 6.557439 6.244998 5.196152 5.196152 5.916080 5.744563 6.480741 5.830952
18 5.744563 5.744563 5.656854 6.000000 5.830952 5.830952 6.082763 5.385165 5.830952 5.291503 6.324555 6.000000 5.656854 5.830952 5.744563 5.744563 6.403124
19 6.244998 6.708204 5.099020 5.656854 5.291503 6.000000 6.082763 5.567764 5.099020 5.291503 5.477226 6.324555 4.242641 5.291503 5.196152 5.000000 5.744563 6.000000
20 5.385165 5.744563 4.000000 4.898979 4.690416 5.477226 4.358899 4.582576 4.000000 5.099020 5.830952 5.477226 4.472136 4.898979 5.196152 4.795832 6.557439 5.656854
21 5.744563 5.744563 6.000000 5.477226 6.480741 5.291503 4.795832 5.567764 5.477226 5.830952 5.830952 6.000000 6.000000 5.656854 6.557439 5.567764 6.557439 5.830952
19 20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 5.477226
21 6.164414 5.656854
> round(krack_friend_advice_dist2,2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2 5.29
3 5.74 6.24
4 5.39 6.08 4.90
5 5.92 6.56 3.74 5.29
6 5.39 5.39 6.00 5.66 6.00
7 5.66 5.29 5.00 5.20 5.92 5.00
8 4.90 4.90 4.58 5.00 5.57 5.00 4.90
9 5.57 5.92 3.74 4.69 4.24 5.66 4.58 4.58
10 5.39 6.71 5.83 5.48 5.83 5.66 5.57 5.74 5.66
11 5.57 5.74 6.16 6.16 6.00 4.90 6.24 5.74 6.16 5.66
12 5.57 4.36 5.66 5.83 6.00 4.24 5.57 4.12 5.29 6.48 5.48
13 5.57 6.08 4.69 5.48 5.29 5.29 5.00 4.80 4.69 5.29 5.66 5.48
14 5.00 5.00 5.10 6.00 5.66 4.24 4.80 4.58 4.69 5.83 4.90 4.69 4.90
15 6.48 6.93 4.12 5.74 4.36 6.86 6.00 5.83 5.20 5.39 6.40 6.56 5.20 6.24
16 5.10 5.29 5.20 5.00 5.57 4.80 5.29 3.46 5.00 5.57 5.20 4.58 4.12 4.80 6.00
17 5.83 6.00 6.56 6.40 6.71 5.39 6.78 5.66 6.56 6.24 5.20 5.20 5.92 5.74 6.48 5.83
18 5.74 5.74 5.66 6.00 5.83 5.83 6.08 5.39 5.83 5.29 6.32 6.00 5.66 5.83 5.74 5.74 6.40
19 6.24 6.71 5.10 5.66 5.29 6.00 6.08 5.57 5.10 5.29 5.48 6.32 4.24 5.29 5.20 5.00 5.74 6.00
20 5.39 5.74 4.00 4.90 4.69 5.48 4.36 4.58 4.00 5.10 5.83 5.48 4.47 4.90 5.20 4.80 6.56 5.66 5.48
21 5.74 5.74 6.00 5.48 6.48 5.29 4.80 5.57 5.48 5.83 5.83 6.00 6.00 5.66 6.56 5.57 6.56 5.83 6.16 5.66
>
Using hclust
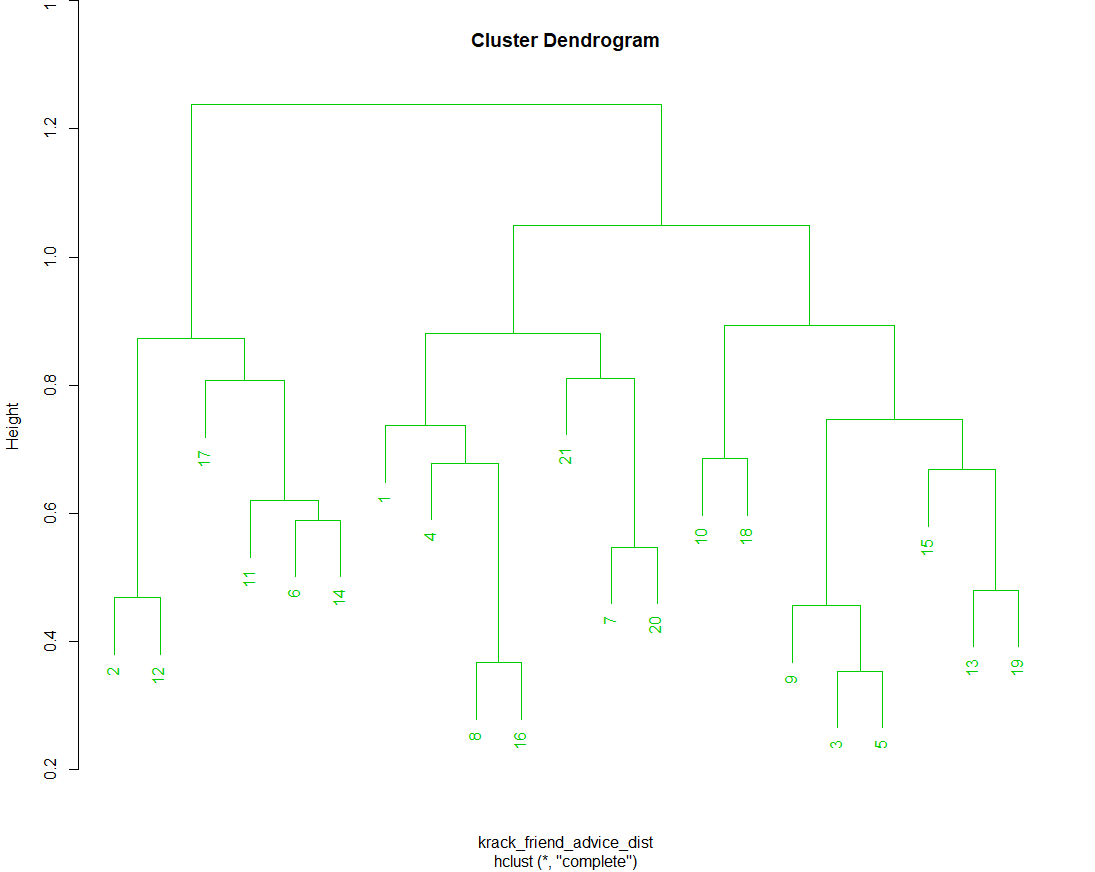
# hclust() performs a hierarchical agglomerative NetCluster # operation based on the values in the dissimilarity matrix # yielded by as.dist() above. The standard visualization is a # dendrogram. By default, hclust() agglomerates clusters via a # "complete linkakage" algorithm, determining cluster proximity # by looking at the distance of the two points across clusters # that are farthest away from one another. This can be changed via # the "method" parameter. krack_friend_advice_hclust <- hclust(krack_friend_advice_dist) plot(krack_friend_advice_hclust)
Using cutree
# cutree() allows us to use the output of hclust() to set # different numbers of clusters and assign vertices to clusters # as appropriate. For example: cutree(krack_friend_advice_hclust, k=2)
> cutree(krack_friend_advice_hclust, k=2) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 1 1 1 2 1 1 1 1 2 2 1 2 1 1 2 1 1 1 1 > >
# Now we'll try to figure out the number of clusters that best
# describes the underlying data. To do this, we'll loop through
# all of the possible numbers of clusters (1 through n, where n is
# the number of actors in the network). For each solution
# corresponding to a given number of clusters, we'll use cutree()
# to assign the vertices to their respective clusters
# corresponding to that solution.
#
# From this, we can generate a matrix of within- and between-
# cluster correlations. Thus, when there is one cluster for each
# vertex in the network, the cell values will be identical to the
# observed correlation matrix, and when there is one cluster for
# the whole network, the values will all be equal to the average
# correlation across the observed matrix.
#
# We can then correlate each by-cluster matrix with the observed
# correlation matrix to see how well the by-cluster matrix fits
# the data. We'll store the correlation for each number of
# clusters in a vector, which we can then plot.
# First, we initialize a vector for storing the correlations and
# set a variable for our number of vertices.
clustered_observed_cors = vector()
num_vertices = length(V(krack_advice))
# Next, we loop through the different possible cluster
# configurations, produce matrices of within- and between-
# cluster correlations, and correlate these by-cluster matrices
# with the observed correlation matrix.
# pdf("6.3_m182_studentnet_task_social_clustered_observed_corrs.pdf")
clustered_observed_cors <-clustConfigurations(num_vertices, krack_friend_advice_hclust, krack_friend_advice_cors)
clustered_observed_cors
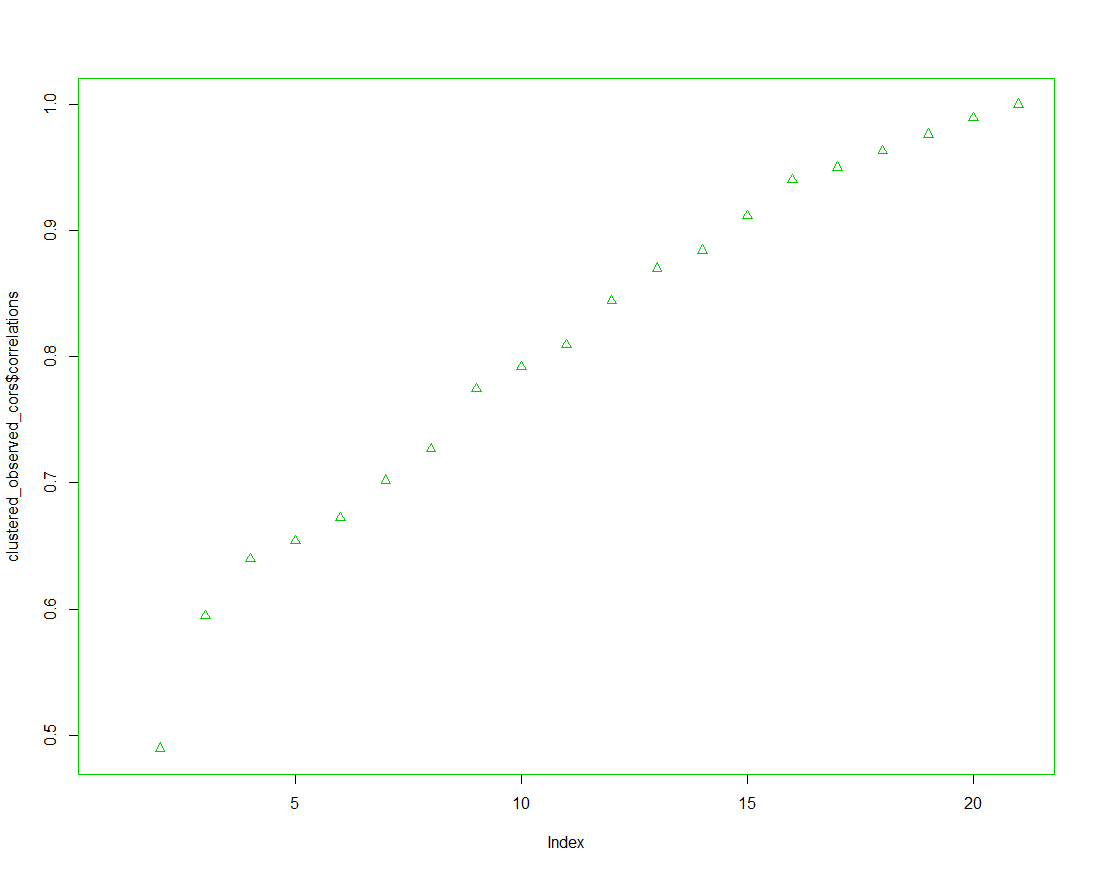
plot(clustered_observed_cors$correlations)
# dev.off()
clustered_observed_cors$correlations
> clustered_observed_cors <-clustConfigurations(num_vertices, krack_friend_advice_hclust, krack_friend_advice_cors) Warning message: In cor(as.vector(d[g1[i], , ]), as.vector(d[g2[j], , ]), use = "complete.obs") : 표준편차가 0입니다 > clustered_observed_cors $label [1] "number of clusters: 1" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 $correlation [1] NA $label [1] "number of clusters: 2" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 1 1 1 2 1 1 1 1 2 2 1 2 1 1 2 1 1 1 1 $correlation [1] 0.4896211 $label [1] "number of clusters: 3" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 1 3 2 1 1 3 3 2 2 3 2 3 1 2 3 3 1 1 $correlation [1] 0.5944114 $label [1] "number of clusters: 4" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 1 3 2 1 1 3 4 2 2 3 2 3 1 2 4 3 1 1 $correlation [1] 0.6398013 $label [1] "number of clusters: 5" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 1 3 2 4 1 3 5 2 2 3 2 3 1 2 5 3 4 4 $correlation [1] 0.6538231 $label [1] "number of clusters: 6" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 1 3 4 5 1 3 6 4 2 3 4 3 1 4 6 3 5 5 $correlation [1] 0.6723019 $label [1] "number of clusters: 7" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 1 3 4 5 1 3 6 4 2 3 4 3 1 4 6 3 5 7 $correlation [1] 0.7019599 $label [1] "number of clusters: 8" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 1 3 4 5 1 3 6 4 2 3 4 3 1 7 6 3 5 8 $correlation [1] 0.727137 $label [1] "number of clusters: 9" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 1 3 4 5 1 3 6 4 2 7 4 7 1 8 6 7 5 9 $correlation [1] 0.7743714 $label [1] "number of clusters: 10" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 4 3 7 5 2 8 5 8 4 9 7 8 6 10 $correlation [1] 0.7919439 $label [1] "number of clusters: 11" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 4 3 7 5 2 8 5 8 4 9 10 8 6 11 $correlation [1] 0.8093965 $label [1] "number of clusters: 12" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 3 8 5 2 9 5 9 7 10 11 9 6 12 $correlation [1] 0.8445199 $label [1] "number of clusters: 13" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 3 8 5 2 9 5 10 7 11 12 9 6 13 $correlation [1] 0.8700886 $label [1] "number of clusters: 14" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 3 8 9 2 10 5 11 7 12 13 10 6 14 $correlation [1] 0.8844067 $label [1] "number of clusters: 15" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 3 8 9 2 10 11 12 7 13 14 10 6 15 $correlation [1] 0.9115517 $label [1] "number of clusters: 16" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 3 8 9 2 10 11 12 7 13 14 10 15 16 $correlation [1] 0.9403353 $label [1] "number of clusters: 17" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 3 8 9 2 10 11 12 7 13 14 15 16 17 $correlation [1] 0.9502702 $label [1] "number of clusters: 18" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 3 8 9 10 11 12 13 7 14 15 16 17 18 $correlation [1] 0.9633198 $label [1] "number of clusters: 19" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 8 9 10 11 12 13 14 7 15 16 17 18 19 $correlation [1] 0.9762881 $label [1] "number of clusters: 20" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 $correlation [1] 0.9895545 $label [1] "number of clusters: 21" $clusters 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 $correlation [1] 1 $correlations [1] NA 0.4896211 0.5944114 0.6398013 0.6538231 0.6723019 0.7019599 0.7271370 0.7743714 0.7919439 0.8093965 0.8445199 0.8700886 0.8844067 0.9115517 0.9403353 [17] 0.9502702 0.9633198 0.9762881 0.9895545 1.0000000 > plot(clustered_observed_cors$correlations) > > clustered_observed_cors$correlations [1] NA 0.4896211 0.5944114 0.6398013 0.6538231 0.6723019 0.7019599 0.7271370 0.7743714 0.7919439 0.8093965 0.8445199 0.8700886 0.8844067 0.9115517 0.9403353 [17] 0.9502702 0.9633198 0.9762881 0.9895545 1.0000000 >
decision on # of clusters
# From a visual inspection of the correlation matrix, we can # decide on the proper number of clusters in this network. # For this network, we'll use 6. (Note that the 1-cluster # solution doesn't appear on the plot because its correlation # with the observed correlation matrix is undefined.) num_clusters = 4 clusters <- cutree(krack_friend_advice_hclust, k = num_clusters) clusters cluster_cor_mat <- clusterCorr(krack_friend_advice_cors, clusters) round(cluster_cor_mat,2) # Let's look at the correlation between this cluster configuration # and the observed correlation matrix. This should match the # corresponding value from clustered_observed_cors above. gcor(cluster_cor_mat, krack_friend_advice_cors)
#####################
# Questions:
# (1) What rationale do you have for selecting the number of
# clusters / positions that you do?
#####################
### NOTE ON DEDUCTIVE CLUSTERING
# It's pretty straightforward, using the code above, to explore
# your own deductive NetCluster. Simply supply your own cluster
# vector, where the elements in the vector are in the same order
# as the vertices in the matrix, and the values represent the
# cluster to which each vertex belongs.
#
# For example, if you believed that actors 2, 7, and 8 formed one
# group, actor 16 former another group, and everyone else formed
# a third group, you could represent this as follows:
deductive_clusters = c(1, 2, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1,
1, 3)
# You could then examine the fitness of this cluster configuration
# as follows:
deductive_cluster_cor_mat <- generate_cluster_cor_mat(krack_friend_advice_cors, deductive_clusters)
deductive_cluster_cor_mat
gcor(deductive_cluster_cor_mat, krack_friend_advice_cors)
### END NOTE ON DEDUCTIVE CLUSTERING
# Now we'll use the 4-cluster solution to generate blockmodels,
# using the raw tie data from the underlying task and social
# networks.
# Friendship valued
friend_mean <- mean(as.matrix(krack_friend_matrix_row_to_col))
friend_mean
friend_valued_blockmodel <- blockmodel(krack_friend_matrix_row_to_col, clusters)
friend_valued_blockmodel
# friend binary
friend_density <- graph.density(krack_friend)
friend_density
friend_binary_blockmodel <- blockmodel(as.matrix(krack_friend_matrix_row_to_col_bin), clusters)
friend_binary_blockmodel
# advice valued
advice_mean <- mean(as.matrix(krack_advice_matrix_row_to_col))
advice_mean
advice_valued_blockmodel <- blockmodel(as.matrix(krack_advice_matrix_row_to_col), clusters)
advice_valued_blockmodel
# advice binary
advice_density <- graph.density(krack_advice)
advice_density
advice_binary_blockmodel <- blockmodel(as.matrix(krack_advice_matrix_row_to_col_bin), clusters)
advice_binary_blockmodel
# We can also permute the network to examine the within- and
# between-cluster correlations.
cluster_cor_mat_per <- permute_matrix(clusters, cluster_cor_mat)
cluster_cor_mat_per
#####################
# Questions:
# (2) What is the story you get from viewing these clusters,
# and their within and between cluster densities on task and
# social interaction? What can you say about M182 from this?
#####################
#####################
# Questions:
# (3) What does clustering of the triadic census afford us?
# What roles do you see? Redo the initial blockmodel analysis
# without social interaction (only task) and then compare to
# this solution. Do they differ?
#
# Extra credit: Try running the triad census on task AND
# social interaction separately and then correlating persons.
# What result do you get? Is it different from our initial
# blockmodel result? Show your code.
######################
###
# 5. FACTOR ANALYSIS
###
# Note that although we are conducting a principal components
# analysis (PCA), which is technically not exactly the same as
# factor analysis, we will use the term "factor" to describe the
# individual components in our PCA.
# PCA is often used in network analysis as a form of detecting
# individuals global positioning. We say "global" because these
# clusters aren't defined on local cohesion but from the overall
# pattern of ties individuals have with all others (structural
# equivalence). Identifying the first two largest components that
# organize the variance in tie patterns is one way of doing this.
# We'll analyze the 4n x n matrix generated above.
# First, we want to determine the ideal number of components
# (factors) to extract. We'll do this by examining the eigenvalues
# in a scree plot and examining how each number of factors stacks
# up to a few proposed non-graphical solutions to selecting the
# optimal number of components, available via the nFactors
# package.
ev <- eigen(cor(as.matrix(krack_reports_to_advice_matrix))) # get eigenvalues
ap <- parallel(subject=nrow(krack_reports_to_advice_matrix),
var=ncol(krack_reports_to_advice_matrix),
rep=100,cent=.05)
nS <- nScree(ev$values, ap$eigen$qevpea)
# pdf("6.6_m182_studentnet_task_social_pca_scree.pdf")
plotnScree(nS)
# To draw a line across the graph where eigenvalues are = 1,
# use the following code:
plotnScree(nS)
abline(h=1)
# dev.off()
# For more information on this procedure, please see
# the references provided in the parallel() documentation
# (type "?parallel" in the R command line with the package
# loaded).
# Now we'll run a principal components analysis on the matrix,
# using the number of factors determined above (note this may not
# be the same number as you get):
pca_krack_reports_to_advice = principal(as.matrix(krack_reports_to_advice_matrix), nfactors=5, rotate="varimax")
# Let's take a look at the results in the R terminal:
pca_krack_reports_to_advice
# You can see the standardized loadings for each factor for each
# node. Note that R sometimes puts the factors in a funky order
# (e.g. RC1, RC2, RC5, RC4, RC3) but all of the factors are there.
# You can see that the SS loadings, proportion of variance
# explained and cumulative variance explained is provided below. A
# Chi Square test of the factors and various other statistics are
# provided below.
# Note that the eigenvalues can be accessed via the following
# command:
pca_krack_reports_to_advice$values
# Now we will use the factor loadings to cluster and compare that
# to our other NetCluster techniques, using dendrograms.
# Take the distance based on Euclidian Distance
krack_reports_to_factor_dist = dist(pca_krack_reports_to_advice$loadings)
# And cluster
krack_reports_to_factor_hclust <- hclust(krack_reports_to_factor_dist)
# pdf("6.7_m182_studentnet_task_social_pca_hclust.pdf")
plot(krack_reports_to_factor_hclust)
# dev.off()
# And compare to NetCluster based on correlations and triads:
# pdf("6.8_m182_task_cluster_by_correlation_PCA_Triads.pdf")
par(mfrow = c(1,2))
plot(krack_reports_to_advice_hclust, main = "Correlation")
plot(krack_reports_to_factor_hclust, main = "PCA")
# plot(m182_task_triad_hclust, main = "Triads")
par(mfrow = c(1,1))
# dev.off()
#####################
# Questions:
# (4) How do the results across blockmodel techniques differ?
# Why might you use one over the other? Why might you want to
# run more than one in your analyses?
#####################
krackhardt_datasets.txt · Last modified: by hkimscil