This is an old revision of the document!
Table of Contents
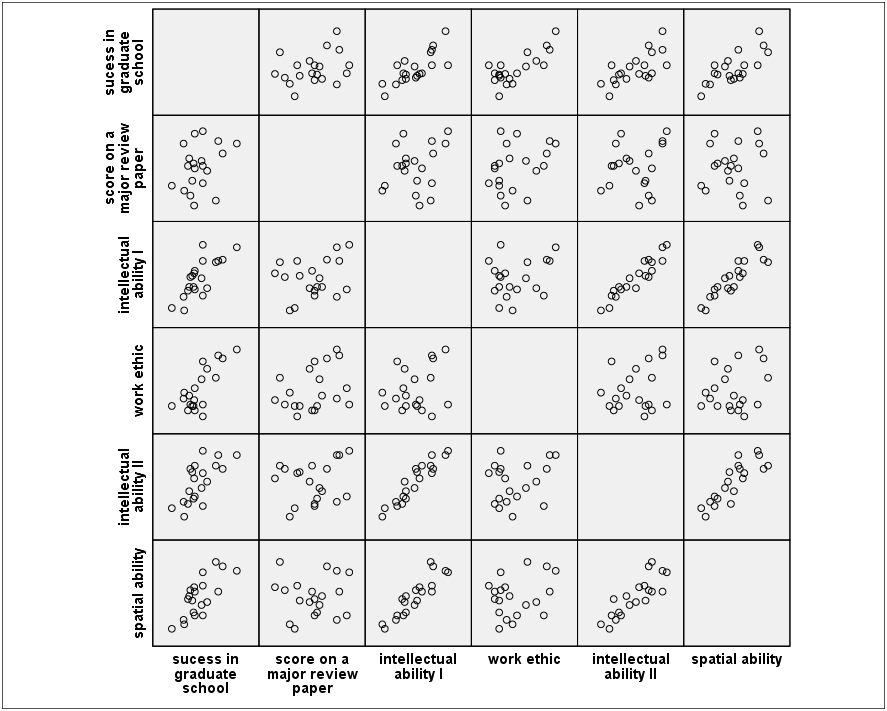
Multiple Regression with Two Predictor Variables
data file: mlt06.sav from http://www.psychstat.missouristate.edu/multibook/mlt06.htm
- Y1 - A measure of success in graduate school.
- X1 - A measure of intellectual ability.
- X2 - A measure of “work ethic.”
- X3 - A second measure of intellectual ability.
- X4 - A measure of spatial ability.
- Y2 - Score on a major review paper.
Analyze
Descriptive statistics
Descriptives
모든 변수를 Variable(s)로 이동
OK 누르기
Descriptive Statistics N Minimum Maximum Mean Std. Deviation sucess in graduate school 20 125 230 169.45 24.517 score on a major review paper 20 105 135 120.50 8.918 intellectual ability I 20 11 64 37.05 14.891 work ethic 20 11 56 29.10 14.056 intellectual ability II 20 17 79 49.35 18.622 spatial ability 20 11 56 32.50 13.004 Valid N (listwise) 20
Correlation matrix 검사
Analyze Correlate Bivariate 모든 변수를 Variable(s)로 이동
Correlations y1 y2 x1 x2 x3 x4 y1 Pearson Correlation 1 .310 .764** .769** .687** .736** Sig. (2-tailed) .184 .000 .000 .001 .000 N 20 20 20 20 20 20 y2 Pearson Correlation .310 1 .251 .334 .168 .018 Sig. (2-tailed) .184 .286 .150 .479 .939 N 20 20 20 20 20 20 x1 Pearson Correlation .764** .251 1 .255 .940** .904** Sig. (2-tailed) .000 .286 .278 .000 .000 N 20 20 20 20 20 20 x2 Pearson Correlation .769** .334 .255 1 .243 .266 Sig. (2-tailed) .000 .150 .278 .302 .257 N 20 20 20 20 20 20 x3 Pearson Correlation .687** .168 .940** .243 1 .847** Sig. (2-tailed) .001 .479 .000 .302 .000 N 20 20 20 20 20 20 x4 Pearson Correlation .736** .018 .904** .266 .847** 1 Sig. (2-tailed) .000 .939 .000 .257 .000 N 20 20 20 20 20 20 ** Correlation is significant at the 0.01 level (2-tailed).
Regression
Analyze
Regression
Linear
Dependent: y1 (success in graduate school)
Independent: x1 (intell. ability)
x2 (work ethic)
Click Statistics (오른쪽 상단 버튼)
Choose
Estimates (under Regression Coefficients)
Model fit
R squared change
Descriptives
Part and partial correlations
Collinearity diagnostics
Model Summaryb Change Statistics Model R R Adjusted Std. Error R F df1 df2 Sig. F Square R Square of the Square Change Change Estimate Change 1 .968a .936 .929 6.541 .936 124.979 2 17 .000 a Predictors: (Constant), work ethic, intellectual ability I b Dependent Variable: success in graduate school
ANOVAa Model Sum of Squares df Mean Square F Sig. 1 Regression 10693.657 2 5346.828 124.979 .000b Residual 727.293 17 42.782 Total 11420.950 19 a Dependent Variable: sucess in graduate school b Predictors: (Constant), work ethic, intellectual ability I
Coefficientsa Model Unstandardized Standardized Correlations Collinearity Coefficients Coefficients Statistics ------------- ----- ------------ -------------------- --------- ---- B Std. Beta t Sig. Zero Partial Part Tolerance VIF Error -order 1 (Constant) 101.222 4.587 22.065 .000 x1 1.000 .104 .608 9.600 .000 .764 .919 .588 .935 1.070 x3 1.071 .110 .614 9.699 .000 .769 .920 .594 .935 1.070 a Dependent Variable: success in graduate school x1 intellectual ability I x3 work ethic
from the above output:
| x | zero-order cor | part cor | squared zero-order cor | squared part cor | shared square cor |
| x1 | .764 | .588 | 0.583696 | 0.345744 | 0.237952 |
| x2 | .769 | .594 | 0.591361 | 0.352836 | 0.238525 |
note that the values of two raws at the last column are similar. The portion is the shared effects from both x1 and x2.
$$ \hat{Y_{i}} = 101.222 + 1.000X1_{i} + 1.071X2_{i} $$
$$ \hat{Y_{i}} = 101.222 + 1.000 \ \text{intell. ability}_{i} + 1.071 \ \text{work ethic}_{i} $$
E.g. 2
?state.x77
US State Facts and Figures
Description
Data sets related to the 50 states of the United States of America.
Usage
state.abb
state.area
state.center
state.division
state.name
state.region
state.x77
Details
R currently contains the following “state” data sets. Note that all data are arranged according to alphabetical order of the state names.
state.abb:
character vector of 2-letter abbreviations for the state names.
state.area:
numeric vector of state areas (in square miles).
state.center:
list with components named x and y giving the approximate geographic center of each state in negative longitude and latitude. Alaska and Hawaii are placed just off the West Coast.
state.division:
factor giving state divisions (New England, Middle Atlantic, South Atlantic, East South Central, West South Central, East North Central, West North Central, Mountain, and Pacific).
state.name:
character vector giving the full state names.
state.region:
factor giving the region (Northeast, South, North Central, West) that each state belongs to.
state.x77:
matrix with 50 rows and 8 columns giving the following statistics in the respective columns.
Population:
population estimate as of July 1, 1975
Income:
per capita income (1974)
Illiteracy:
illiteracy (1970, percent of population)
Life Exp:
life expectancy in years (1969–71)
Murder:
murder and non-negligent manslaughter rate per 100,000 population (1976)
HS Grad:
percent high-school graduates (1970)
Frost:
mean number of days with minimum temperature below freezing (1931–1960) in capital or large city
Area:
land area in square miles
Source
U.S. Department of Commerce, Bureau of the Census (1977) Statistical Abstract of the United States.
U.S. Department of Commerce, Bureau of the Census (1977) County and City Data Book.
References
Becker, R. A., Chambers, J. M. and Wilks, A. R. (1988) The New S Language. Wadsworth & Brooks/Cole.
> state.x77 # output not shown > str(state.x77) # clearly not a data frame! (it's a matrix) > st = as.data.frame(state.x77) # so we'll make it one > str(st) 'data.frame': 50 obs. of 8 variables: $ Population: num 3615 365 2212 2110 21198 ... $ Income : num 3624 6315 4530 3378 5114 ... $ Illiteracy: num 2.1 1.5 1.8 1.9 1.1 0.7 1.1 0.9 1.3 2 ... $ Life Exp : num 69.0 69.3 70.5 70.7 71.7 ... $ Murder : num 15.1 11.3 7.8 10.1 10.3 6.8 3.1 6.2 10.7 13.9 ... $ HS Grad : num 41.3 66.7 58.1 39.9 62.6 63.9 56 54.6 52.6 40.6 ... $ Frost : num 20 152 15 65 20 166 139 103 11 60 ... $ Area : num 50708 566432 113417 51945 156361 ...
> colnames(st)[4] = "Life.Exp" # no spaces in variable names, please > colnames(st)[6] = "HS.Grad" # ditto > st$Density = st$Population * 1000 / st$Area # create a new column in st
> summary(st)
Population Income Illiteracy Life.Exp Murder
Min. : 365 Min. :3098 Min. :0.500 Min. :67.96 Min. : 1.400
1st Qu.: 1080 1st Qu.:3993 1st Qu.:0.625 1st Qu.:70.12 1st Qu.: 4.350
Median : 2838 Median :4519 Median :0.950 Median :70.67 Median : 6.850
Mean : 4246 Mean :4436 Mean :1.170 Mean :70.88 Mean : 7.378
3rd Qu.: 4968 3rd Qu.:4814 3rd Qu.:1.575 3rd Qu.:71.89 3rd Qu.:10.675
Max. :21198 Max. :6315 Max. :2.800 Max. :73.60 Max. :15.100
HS.Grad Frost Area Density
Min. :37.80 Min. : 0.00 Min. : 1049 Min. : 0.6444
1st Qu.:48.05 1st Qu.: 66.25 1st Qu.: 36985 1st Qu.: 25.3352
Median :53.25 Median :114.50 Median : 54277 Median : 73.0154
Mean :53.11 Mean :104.46 Mean : 70736 Mean :149.2245
3rd Qu.:59.15 3rd Qu.:139.75 3rd Qu.: 81162 3rd Qu.:144.2828
Max. :67.30 Max. :188.00 Max. :566432 Max. :975.0033
> cor(st) # correlation matrix (not shown, yet)
> round(cor(st), 3) # rounding makes it easier to look at
Population Income Illiteracy Life.Exp Murder HS.Grad Frost Area Density
Population 1.000 0.208 0.108 -0.068 0.344 -0.098 -0.332 0.023 0.246
Income 0.208 1.000 -0.437 0.340 -0.230 0.620 0.226 0.363 0.330
Illiteracy 0.108 -0.437 1.000 -0.588 0.703 -0.657 -0.672 0.077 0.009
Life.Exp -0.068 0.340 -0.588 1.000 -0.781 0.582 0.262 -0.107 0.091
Murder 0.344 -0.230 0.703 -0.781 1.000 -0.488 -0.539 0.228 -0.185
HS.Grad -0.098 0.620 -0.657 0.582 -0.488 1.000 0.367 0.334 -0.088
Frost -0.332 0.226 -0.672 0.262 -0.539 0.367 1.000 0.059 0.002
Area 0.023 0.363 0.077 -0.107 0.228 0.334 0.059 1.000 -0.341
Density 0.246 0.330 0.009 0.091 -0.185 -0.088 0.002 -0.341 1.000
>
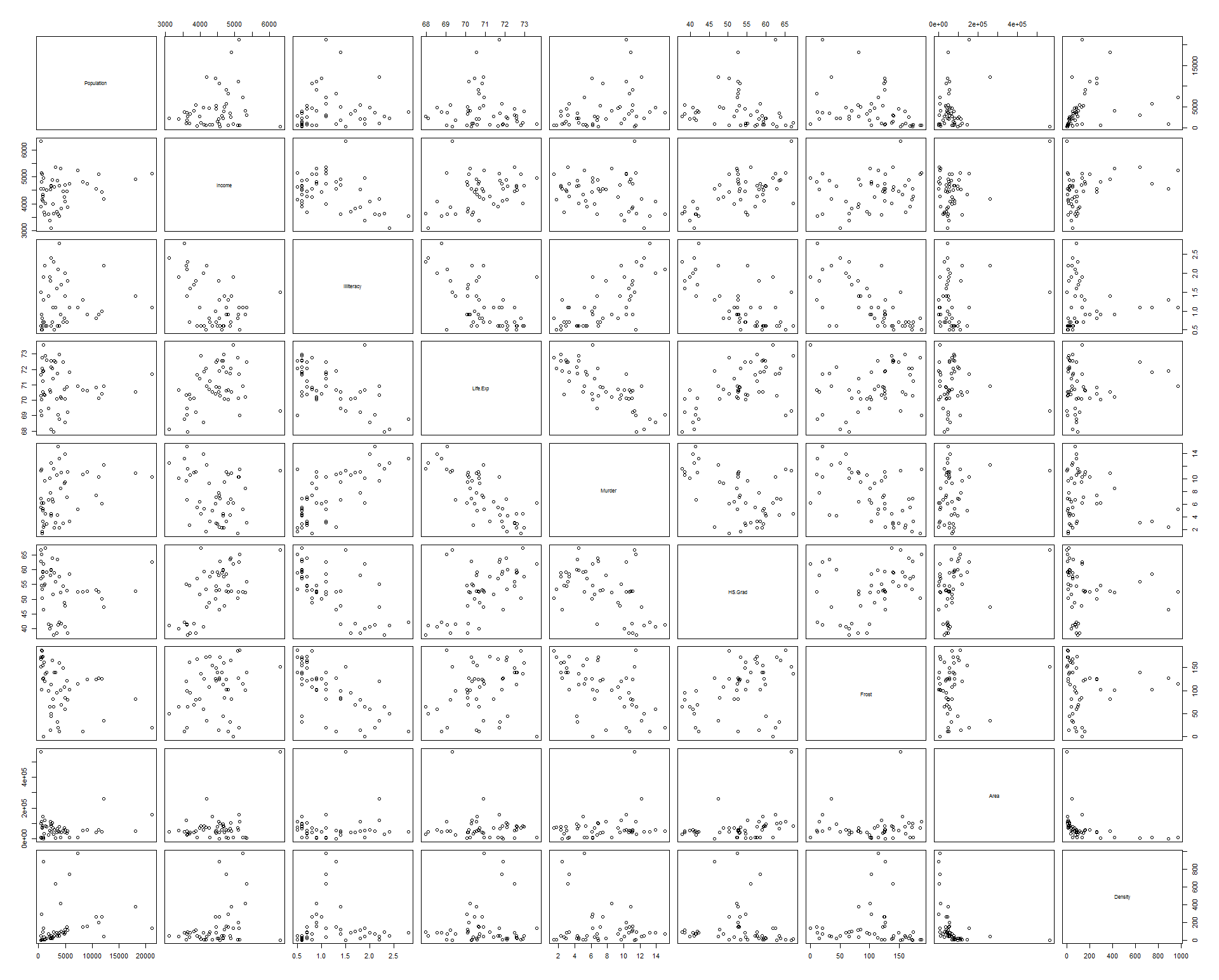
> pairs(st) # scatterplot matrix; plot(st) does the same thing
> ### model1 = lm(Life.Exp ~ Population + Income + Illiteracy + Murder +
+ ### HS.Grad + Frost + Area + Density, data=st)
> ### This is what we're going to accomplish, but more economically, by
> ### simply placing a dot after the tilde, which means "everything else."
> model1 = lm(Life.Exp ~ ., data=st)
> summary(model1)
Call:
lm(formula = Life.Exp ~ ., data = st)
Residuals:
Min 1Q Median 3Q Max
-1.47514 -0.45887 -0.06352 0.59362 1.21823
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.995e+01 1.843e+00 37.956 < 2e-16 ***
Population 6.480e-05 3.001e-05 2.159 0.0367 *
Income 2.701e-04 3.087e-04 0.875 0.3867
Illiteracy 3.029e-01 4.024e-01 0.753 0.4559
Murder -3.286e-01 4.941e-02 -6.652 5.12e-08 ***
HS.Grad 4.291e-02 2.332e-02 1.840 0.0730 .
Frost -4.580e-03 3.189e-03 -1.436 0.1585
Area -1.558e-06 1.914e-06 -0.814 0.4205
Density -1.105e-03 7.312e-04 -1.511 0.1385
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7337 on 41 degrees of freedom
Multiple R-squared: 0.7501, Adjusted R-squared: 0.7013
F-statistic: 15.38 on 8 and 41 DF, p-value: 3.787e-10
> summary.aov(model1)
Df Sum Sq Mean Sq F value Pr(>F)
Population 1 0.409 0.409 0.760 0.38849
Income 1 11.595 11.595 21.541 3.53e-05 ***
Illiteracy 1 19.421 19.421 36.081 4.23e-07 ***
Murder 1 27.429 27.429 50.959 1.05e-08 ***
HS.Grad 1 4.099 4.099 7.615 0.00861 **
Frost 1 2.049 2.049 3.806 0.05792 .
Area 1 0.001 0.001 0.002 0.96438
Density 1 1.229 1.229 2.283 0.13847
Residuals 41 22.068 0.538
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
Model fitting
> model2 = update(model1, .~. -Area)
> summary(model2)
Call:
lm(formula = Life.Exp ~ Population + Income + Illiteracy + Murder +
HS.Grad + Frost + Density, data = st)
Residuals:
Min 1Q Median 3Q Max
-1.50252 -0.40471 -0.06079 0.58682 1.43862
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.094e+01 1.378e+00 51.488 < 2e-16 ***
Population 6.249e-05 2.976e-05 2.100 0.0418 *
Income 1.485e-04 2.690e-04 0.552 0.5840
Illiteracy 1.452e-01 3.512e-01 0.413 0.6814
Murder -3.319e-01 4.904e-02 -6.768 3.12e-08 ***
HS.Grad 3.746e-02 2.225e-02 1.684 0.0996 .
Frost -5.533e-03 2.955e-03 -1.873 0.0681 .
Density -7.995e-04 6.251e-04 -1.279 0.2079
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7307 on 42 degrees of freedom
Multiple R-squared: 0.746, Adjusted R-squared: 0.7037
F-statistic: 17.63 on 7 and 42 DF, p-value: 1.173e-10
> anova(model2, model1)
Analysis of Variance Table
Model 1: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Density
Model 2: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Area + Density
Res.Df RSS Df Sum of Sq F Pr(>F)
1 42 22.425
2 41 22.068 1 0.35639 0.6621 0.4205
> model3 = update(model2, .~. -Illiteracy)
> summary(model3)
Call:
lm(formula = Life.Exp ~ Population + Income + Murder + HS.Grad +
Frost + Density, data = st)
Residuals:
Min 1Q Median 3Q Max
-1.49555 -0.41246 -0.05336 0.58399 1.50535
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.131e+01 1.042e+00 68.420 < 2e-16 ***
Population 5.811e-05 2.753e-05 2.110 0.0407 *
Income 1.324e-04 2.636e-04 0.502 0.6181
Murder -3.208e-01 4.054e-02 -7.912 6.32e-10 ***
HS.Grad 3.499e-02 2.122e-02 1.649 0.1065
Frost -6.191e-03 2.465e-03 -2.512 0.0158 *
Density -7.324e-04 5.978e-04 -1.225 0.2272
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7236 on 43 degrees of freedom
Multiple R-squared: 0.745, Adjusted R-squared: 0.7094
F-statistic: 20.94 on 6 and 43 DF, p-value: 2.632e-11
>
> model4 = update(model3, .~. -Income)
> summary(model4)
Call:
lm(formula = Life.Exp ~ Population + Murder + HS.Grad + Frost +
Density, data = st)
Residuals:
Min 1Q Median 3Q Max
-1.56877 -0.40951 -0.04554 0.57362 1.54752
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.142e+01 1.011e+00 70.665 < 2e-16 ***
Population 6.083e-05 2.676e-05 2.273 0.02796 *
Murder -3.160e-01 3.910e-02 -8.083 3.07e-10 ***
HS.Grad 4.233e-02 1.525e-02 2.776 0.00805 **
Frost -5.999e-03 2.414e-03 -2.485 0.01682 *
Density -5.864e-04 5.178e-04 -1.132 0.26360
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7174 on 44 degrees of freedom
Multiple R-squared: 0.7435, Adjusted R-squared: 0.7144
F-statistic: 25.51 on 5 and 44 DF, p-value: 5.524e-12
> model5 = update(model4, .~. -Density)
> summary(model5)
Call:
lm(formula = Life.Exp ~ Population + Murder + HS.Grad + Frost,
data = st)
Residuals:
Min 1Q Median 3Q Max
-1.47095 -0.53464 -0.03701 0.57621 1.50683
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.103e+01 9.529e-01 74.542 < 2e-16 ***
Population 5.014e-05 2.512e-05 1.996 0.05201 .
Murder -3.001e-01 3.661e-02 -8.199 1.77e-10 ***
HS.Grad 4.658e-02 1.483e-02 3.142 0.00297 **
Frost -5.943e-03 2.421e-03 -2.455 0.01802 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7197 on 45 degrees of freedom
Multiple R-squared: 0.736, Adjusted R-squared: 0.7126
F-statistic: 31.37 on 4 and 45 DF, p-value: 1.696e-12
>
> anova(model5, model1)
Analysis of Variance Table
Model 1: Life.Exp ~ Population + Murder + HS.Grad + Frost
Model 2: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Area + Density
Res.Df RSS Df Sum of Sq F Pr(>F)
1 45 23.308
2 41 22.068 4 1.2397 0.5758 0.6818
Stepwise
> step(model1, direction="backward")
Start: AIC=-22.89
Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad +
Frost + Area + Density
Df Sum of Sq RSS AIC
- Illiteracy 1 0.3050 22.373 -24.208
- Area 1 0.3564 22.425 -24.093
- Income 1 0.4120 22.480 -23.969
<none> 22.068 -22.894
- Frost 1 1.1102 23.178 -22.440
- Density 1 1.2288 23.297 -22.185
- HS.Grad 1 1.8225 23.891 -20.926
- Population 1 2.5095 24.578 -19.509
- Murder 1 23.8173 45.886 11.707
Step: AIC=-24.21
Life.Exp ~ Population + Income + Murder + HS.Grad + Frost + Area +
Density
Df Sum of Sq RSS AIC
- Area 1 0.1427 22.516 -25.890
- Income 1 0.2316 22.605 -25.693
<none> 22.373 -24.208
- Density 1 0.9286 23.302 -24.174
- HS.Grad 1 1.5218 23.895 -22.918
- Population 1 2.2047 24.578 -21.509
- Frost 1 3.1324 25.506 -19.656
- Murder 1 26.7071 49.080 13.072
Step: AIC=-25.89
Life.Exp ~ Population + Income + Murder + HS.Grad + Frost + Density
Df Sum of Sq RSS AIC
- Income 1 0.132 22.648 -27.598
- Density 1 0.786 23.302 -26.174
<none> 22.516 -25.890
- HS.Grad 1 1.424 23.940 -24.824
- Population 1 2.332 24.848 -22.962
- Frost 1 3.304 25.820 -21.043
- Murder 1 32.779 55.295 17.033
Step: AIC=-27.6
Life.Exp ~ Population + Murder + HS.Grad + Frost + Density
Df Sum of Sq RSS AIC
- Density 1 0.660 23.308 -28.161
<none> 22.648 -27.598
- Population 1 2.659 25.307 -24.046
- Frost 1 3.179 25.827 -23.030
- HS.Grad 1 3.966 26.614 -21.529
- Murder 1 33.626 56.274 15.910
Step: AIC=-28.16
Life.Exp ~ Population + Murder + HS.Grad + Frost
Df Sum of Sq RSS AIC
<none> 23.308 -28.161
- Population 1 2.064 25.372 -25.920
- Frost 1 3.122 26.430 -23.877
- HS.Grad 1 5.112 28.420 -20.246
- Murder 1 34.816 58.124 15.528
Call:
lm(formula = Life.Exp ~ Population + Murder + HS.Grad + Frost,
data = st)
Coefficients:
(Intercept) Population Murder HS.Grad Frost
7.103e+01 5.014e-05 -3.001e-01 4.658e-02 -5.943e-03
>
Prediction
> predict(model5, list(Population=2000, Murder=10.5, HS.Grad=48, Frost=100))
1
69.61746
Regression Diagnostics
> par(mfrow=c(2,2)) # visualize four graphs at once > plot(model5) > par(mfrow=c(1,1)) # reset the graphics defaults
Model objects
> names(model5) [1] "coefficients" "residuals" "effects" "rank" "fitted.values" [6] "assign" "qr" "df.residual" "xlevels" "call" [11] "terms" "model"
> coef(model5) # an extractor function (Intercept) Population Murder HS.Grad Frost 7.102713e+01 5.013998e-05 -3.001488e-01 4.658225e-02 -5.943290e-03 > model5$coefficients # list indexing (Intercept) Population Murder HS.Grad Frost 7.102713e+01 5.013998e-05 -3.001488e-01 4.658225e-02 -5.943290e-03 > model5[[1]] # recall by position in the list (double brackets for lists) (Intercept) Population Murder HS.Grad Frost 7.102713e+01 5.013998e-05 -3.001488e-01 4.658225e-02 -5.943290e-03
> model5$resid
Alabama Alaska Arizona Arkansas California
0.56888134 -0.54740399 -0.86415671 1.08626119 -0.08564599
Colorado Connecticut Delaware Florida Georgia
0.95645816 0.44541028 -1.06646884 0.04460505 -0.09694227
Hawaii Idaho Illinois Indiana Iowa
1.50683146 0.37010714 -0.05244160 -0.02158526 0.16347124
Kansas Kentucky Louisiana Maine Maryland
0.67648037 0.85582067 -0.39044846 -1.47095411 -0.29851996
Massachusetts Michigan Minnesota Mississippi Missouri
-0.61105391 0.76106640 0.69440380 -0.91535384 0.58389969
Montana Nebraska Nevada New Hampshire New Jersey
-0.84024805 0.42967691 -0.49482393 -0.49635615 -0.66612086
New Mexico New York North Carolina North Dakota Ohio
0.28880945 -0.07937149 -0.07624179 0.90350550 -0.26548767
Oklahoma Oregon Pennsylvania Rhode Island South Carolina
0.26139958 -0.28445333 -0.95045527 0.13992982 -1.10109172
South Dakota Tennessee Texas Utah Vermont
0.06839119 0.64416651 0.92114057 0.84246817 0.57865019
Virginia Washington West Virginia Wisconsin Wyoming
-0.06691392 -0.96272426 -0.96982588 0.47004324 -0.58678863
> sort(model5$resid) # extract residuals and sort them
Maine South Carolina Delaware West Virginia Washington
-1.47095411 -1.10109172 -1.06646884 -0.96982588 -0.96272426
Pennsylvania Mississippi Arizona Montana New Jersey
-0.95045527 -0.91535384 -0.86415671 -0.84024805 -0.66612086
Massachusetts Wyoming Alaska New Hampshire Nevada
-0.61105391 -0.58678863 -0.54740399 -0.49635615 -0.49482393
Louisiana Maryland Oregon Ohio Georgia
-0.39044846 -0.29851996 -0.28445333 -0.26548767 -0.09694227
California New York North Carolina Virginia Illinois
-0.08564599 -0.07937149 -0.07624179 -0.06691392 -0.05244160
Indiana Florida South Dakota Rhode Island Iowa
-0.02158526 0.04460505 0.06839119 0.13992982 0.16347124
Oklahoma New Mexico Idaho Nebraska Connecticut
0.26139958 0.28880945 0.37010714 0.42967691 0.44541028
Wisconsin Alabama Vermont Missouri Tennessee
0.47004324 0.56888134 0.57865019 0.58389969 0.64416651
Kansas Minnesota Michigan Utah Kentucky
0.67648037 0.69440380 0.76106640 0.84246817 0.85582067
North Dakota Texas Colorado Arkansas Hawaii
0.90350550 0.92114057 0.95645816 1.08626119 1.50683146