Table of Contents
Outliers e.g.,
This is further reading for detecting outliers, adopted from http://www.ats.ucla.edu/stat/spss/webbooks/reg/chapter2/spssreg2.htm .
get file = "DirectoryOfYourComputer\crime.sav". descriptives /var=crime murder pctmetro pctwhite pcths poverty single.
Descriptive Statistics N Minimum Maximum Mean Std. Deviation violent crime rate 51 82 2922 612.84 441.100 murder rate 51 1.60 78.50 8.7275 10.71758 pct metropolitan 51 24.00 100.00 67.3902 21.95713 pct white 51 31.80 98.50 84.1157 13.25839 pct hs graduates 51 64.30 86.60 76.2235 5.59209 pct poverty 51 8.00 26.40 14.2588 4.58424 pct single parent 51 8.40 22.10 11.3255 2.12149 Valid N (listwise) 51
pcmetro, poverty, single을 이용하여 crime을 예측한다고 가정해보자. 즉, pctmetro, poverty, single을 독립변인으로 하고 crime을 종속변인으로 하여 회귀분석을 실시해 보려고 한다. 변인에 대한 설명은 아래와 같다.
| crime: | violent crime rate |
| murder: | murder rate |
| pctmetro: | pct metropolitan |
| pectwhite: | pct white |
| pcths: | pct hs graduates |
| poverty: | pct poverty |
| single: | pct single parent |
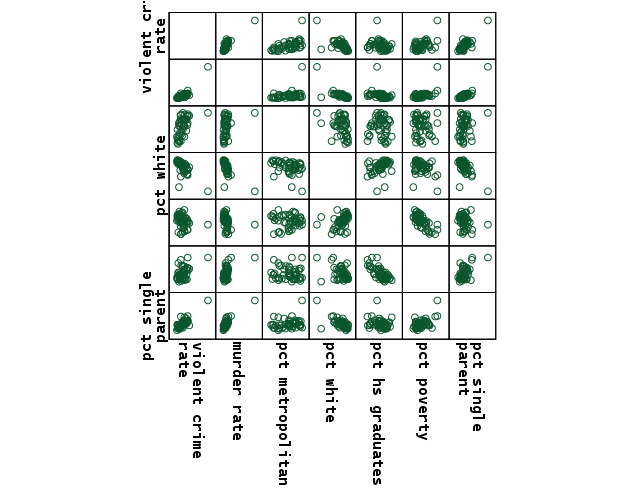
우선 각 변인들의 전반적인 상관관계를 보여주는 스캐터플롯(scatter plot)을 보면 아래와 같다.
graph /scatterplot(matrix)=crime murder pctmetro pctwhite pcths poverty single .
처음에 위치하는 종속변인 크라임과 다른 변인들 간의 상관관계 scatterplot을 보면 동떨어진 케이스가 존재함을 알 수 있다. 이 케이스를 좀더 살펴보고 꼭 필요한 것인지, 잘못된 곳은 없는지, 숫자측정변인으로서 아웃라이어에 해당하므로 제거하고 분석하는 것이 좋을래는지 등등에 대해서 판단해야 한다.
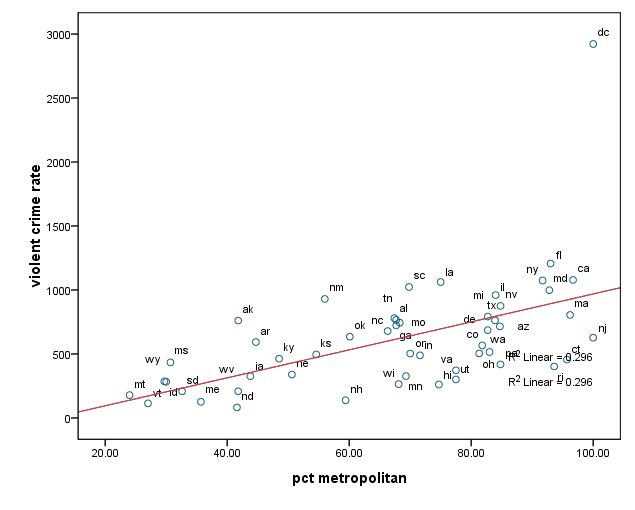
GRAPH /SCATTERPLOT(BIVAR)=pctmetro WITH crime BY state(name) .
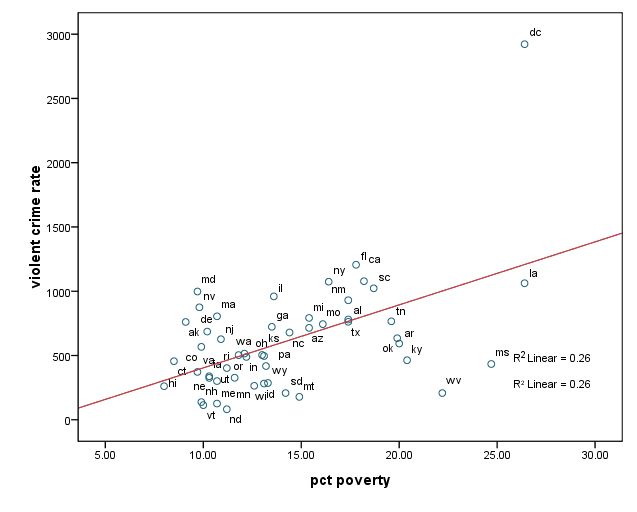
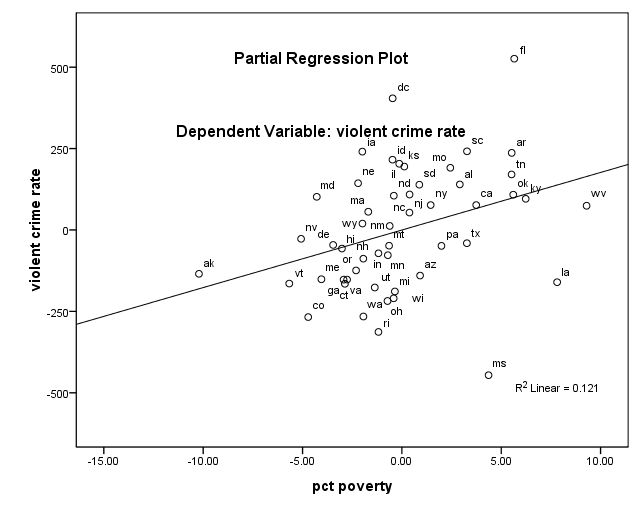
GRAPH /SCATTERPLOT(BIVAR)=poverty WITH crime BY state(name) .
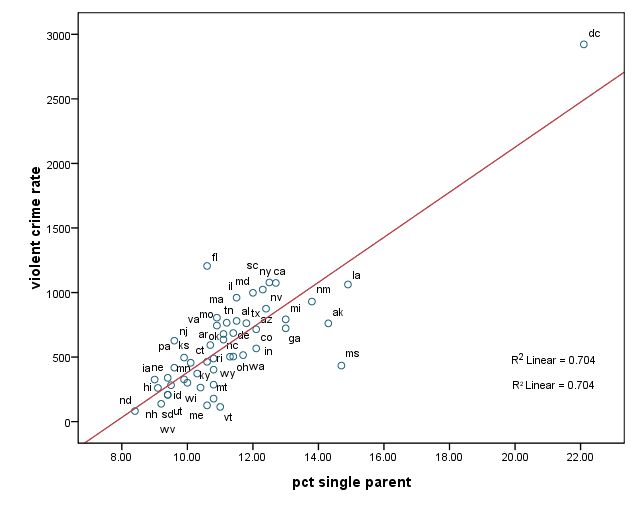
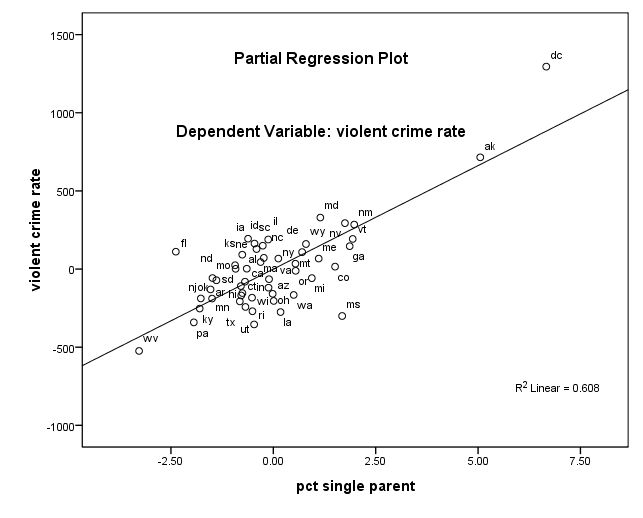
GRAPH /SCATTERPLOT(BIVAR)=single WITH crime BY state(name) .
위의 세 그래프 모두, dc가 문제가 될 것 같다는 여지를 보여준다. 나중에 비교를 위해서 dc에 대한 아무런 조치를 취하지 않은채 (아래와 같이) pcmetro, poverty, single을 이용하여 crime rate를 예측하는 회귀분석을 실시해 본다.
regression /dependent crime /method=enter pctmetro poverty single.
Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .916a .840 .830 182.068 a. Predictors: (Constant), pct single parent, pct metropolitan, pct poverty ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 8170480.211 3 2723493.404 82.160 .000a Residual 1557994.534 47 33148.820 Total 9728474.745 50 a. Predictors: (Constant), pct single parent, pct metropolitan, pct poverty b. Dependent Variable: violent crime rate Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) -1666.436 147.852 -11.271 .000 pct metropolitan 7.829 1.255 .390 6.240 .000 pct poverty 17.680 6.941 .184 2.547 .014 pct single parent 132.408 15.503 .637 8.541 .000 a. Dependent Variable: violent crime rate
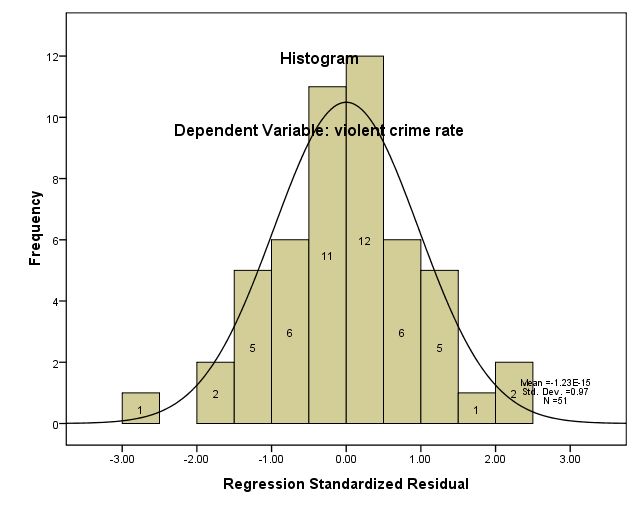
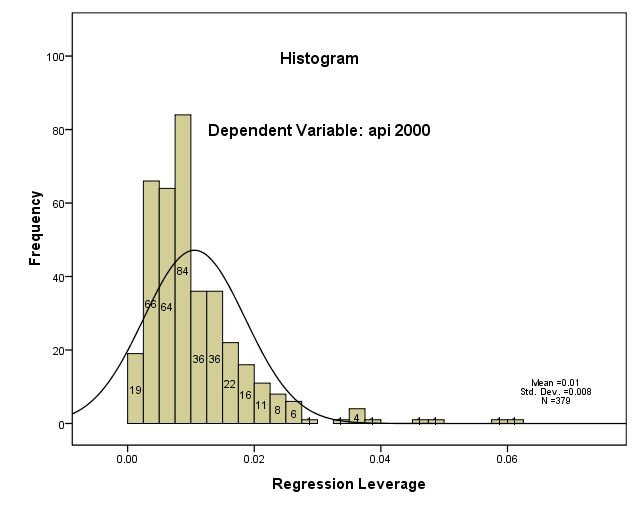
위에서 실시한 회귀분석 후에 residual(예측에 실패한 오차)를 모아 histogram을 만들어 보기로 하자. 아래의 마지막 명령어가 이에 해당한다.
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram.
Model Summary(b) Model R R Square Adjusted R Square Std. Error of the Estimate 1 .916a .840 .830 182.068 a. Predictors: (Constant), pct single parent, pct metropolitan, pct poverty b. Dependent Variable: violent crime rate ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 8170480.211 3 2723493.404 82.160 .000a Residual 1557994.534 47 33148.820 Total 9728474.745 50 a. Predictors: (Constant), pct single parent, pct metropolitan, pct poverty b. Dependent Variable: violent crime rate Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) -1666.436 147.852 -11.271 .000 pct metropolitan 7.829 1.255 .390 6.240 .000 pct poverty 17.680 6.941 .184 2.547 .014 pct single parent 132.408 15.503 .637 8.541 .000 a. Dependent Variable: violent crime rate Residuals Statistics(a) Minimum Maximum Mean Std.Deviation N Predicted Value -30.51 2509.43 612.84 404.240 51 Residual -523.013 426.111 .000 176.522 51 Std. Predicted Value -1.592 4.692 .000 1.000 51 Std. Residual -2.873 2.340 .000 .970 51 a. Dependent Variable: violent crime rate
위의 그림이 보여 주는 것은 -3.00과 2.00이 각각 넘는 부분의 오차가 다른 케이스와 달리 크다는 것을 알 수 있다.
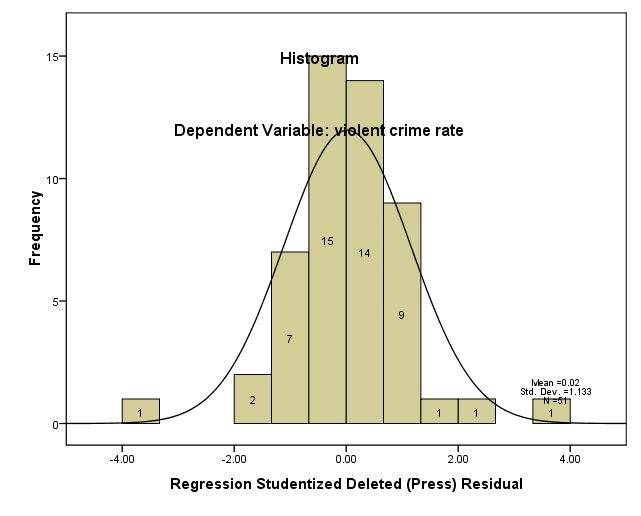
아래는 student deleted residual을 이용하여 histogram을 다시 그리도록 하는 명령어이다. student deleted residual은 회귀분석에서 각 케이스를 제외하고 분석했을 때 얻은 예측치를 사용하여 얻은 잔차를 (residual) 말한다.
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid).
Outlier가 존재한다는 판단하에 outliers(sdresid)와 id(state)를 이용해서 이들이 누구인지 파악해 본다. 이 명령어는 10개의 가장 그단적인 측정치를 보여준다. 아래의 아웃풋을 보면 “dc”가 가장 큰 값을 가지고 있고 (3.766), 다음으로 “ms” (-3.571) 그리고 “fl” (2.620) 순이라는 것을 알 수 있다.
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid) id(state) outliers(sdresid).
see at Analyzing Residuals Document for sdresid (studentized deleted residuals).
Residuals Statistics(a) Minimum Maximum Mean Std. Deviation N Predicted Value -30.51 2509.43 612.84 404.240 51 Std. Predicted Value -1.592 4.692 .000 1.000 51 Standard Error of Predicted Value 25.788 133.343 47.561 18.563 51 Adjusted Predicted Value -39.26 2032.11 605.66 369.075 51 Residual -523.013 426.111 .000 176.522 51 Std. Residual -2.873 2.340 .000 .970 51 Stud. Residual -3.194 3.328 .015 1.072 51 Deleted Residual -646.503 889.885 7.183 223.668 51 Stud. Deleted Residual -3.571 3.766 .018 1.133 51 Mahal. Distance .023 25.839 2.941 4.014 51 Cook's Distance .000 3.203 .089 .454 51 Centered Leverage Value .000 .517 .059 .080 51 a. Dependent Variable: violent crime rate
/casewise 명령어를 이용해서 sdresid 극단치 중 2를 넘는 것을 알아 볼 수 있다. 아래, Casewise Diagnostics(a) 참조.
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid) id(state) outliers(sdresid) /casewise=plot(sdresid) outliers(2) .
Casewise Diagnostics(a) Case Number state Stud. Deleted violent crime Predicted Residual Residual rate Value 9 fl 2.620 1206 779.89 426.111 25 ms -3.571 434 957.01 -523.013 51 dc 3.766 2922 2509.43 412.566 a. Dependent Variable: violent crime rate
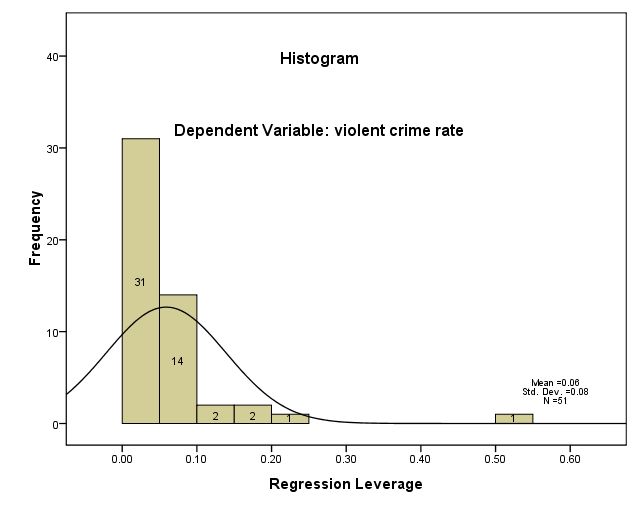
leverage 값을 살펴보는 방법이 아래에 제시된다. leverage 값은 회귀계수 추정치(regression coefficient estimates)에 큰 영향을 주는 값을 말하는데 histogram() 명령어와 outliers() 명령어 옵션으로 활용할 수 있다. 이 값은 일반적으로 (2k+2)/n 를 넘지 않아야 하며, 넘는 다면 아웃라이어로 추정될 수 있으니 주목할 필요가 있다. 여기서 k는 변인의 숫자, n은 케이스 숫자를 말한다. 따라서 (2*3+2)/51 의 계산으로 얻은 .1568 을 넘는 leverage 값을 갖는 케이스를 살펴봐야 한다.
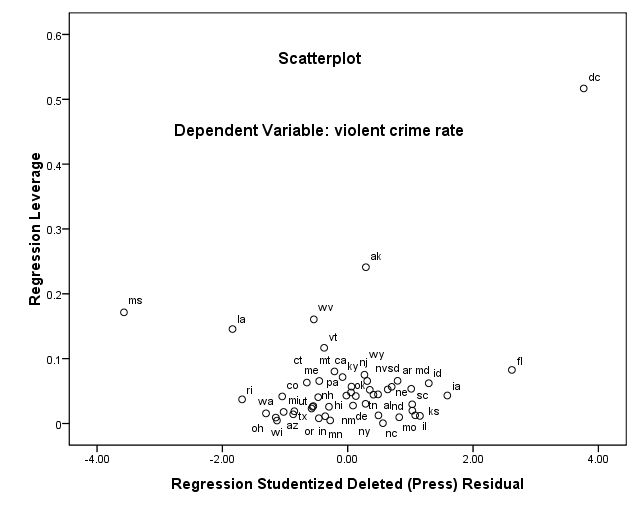
아래의 아웃풋을 보면 fl의 경우에는 stduent deleted residual값은 극단적인 마이너스 값을 갖지만, leverage값은 극단적이 아니므로 fl은 분석에 포함되는 것이 옳은 판단일 수도 있겠다. 그러나, dc의 경우에는 leverage값으로도 극단적이라는 평가를 받게 된다.
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid lever) id(state) outliers(sdresid lever) /casewise=plot(sdresid) outliers(2).
Outlier Statistics(a) Case state Statistic Number Stud. Deleted Residual 1 51 dc 3.766 2 25 ms -3.571 3 9 fl 2.620 4 18 la -1.839 5 39 ri -1.686 6 12 ia 1.590 7 47 wa -1.304 8 13 id 1.293 9 14 il 1.152 10 35 oh -1.148 Centered Leverage Value 1 51 dc .517 2 1 ak .241 3 25 ms .171 4 49 wv .161 5 18 la .146 6 46 vt .117 7 9 fl .083 8 26 mt .080 9 31 nj .075 10 17 ky .072 a. Dependent Variable: violent crime rate
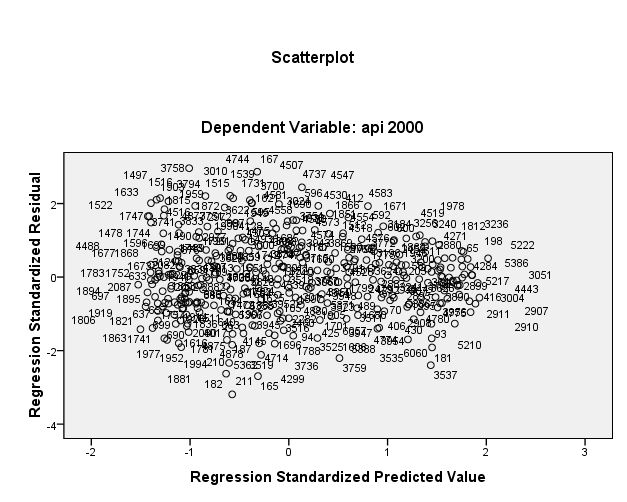
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid lever) id(state) outliers(sdresid, lever) /casewise=plot(sdresid) outliers(2) /scatterplot(*lever, *sdresid).
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid lever) id(state) outliers(sdresid, lever, cook) /casewise=plot(sdresid) outliers(2) cook dffit /scatterplot(*lever, *sdresid).
Casewise Diagnostics(a) Case Number state Stud. violent Cook's DFFIT Deleted crime Distance Residual rate 9 fl 2.620 1206 .174 48.507 25 ms -3.571 434 .602 -123.490 51 dc 3.766 2922 3.203 477.319 a. Dependent Variable: violent crime rate Outlier Statistics(a) Case Number state Statis Sig. F Stud. 1 51 dc 3.766 Deleted 2 25 ms -3.571 Residual 3 9 fl 2.620 4 18 la -1.839 5 39 ri -1.686 6 12 ia 1.590 7 47 wa -1.304 8 13 id 1.293 9 14 il 1.152 10 35 oh -1.148 Cook's 1 51 dc 3.203 .021 Distance 2 25 ms .602 .663 3 9 fl .174 .951 4 18 la .159 .958 5 39 ri .041 .997 6 12 ia .041 .997 7 13 id .037 .997 8 20 md .020 .999 9 6 co .018 .999 10 49 wv .016 .999 Centered 1 51 dc .517 Leverage 2 1 ak .241 Value 3 25 ms .171 4 49 wv .161 5 18 la .146 6 46 vt .117 7 9 fl .083 8 26 mt .080 9 31 nj .075 10 17 ky .072 a. Dependent Variable: violent crime rate
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid lever) id(state) outliers(sdresid, lever, cook) /casewise=plot(sdresid) outliers(2) cook dffit /scatterplot(*lever, *sdresid) /save sdbeta(sdfb).
list /variables state sdfb1 sdfb2 sdfb3 /cases from 1 to 10.
state sdfb1 sdfb2 sdfb3 ak -.10618 -.13134 .14518 al .01243 .05529 -.02751 ar -.06875 .17535 -.10526 az -.09476 -.03088 .00124 ca .01264 .00880 -.00364 co -.03705 .19393 -.13846 ct -.12016 .07446 .03017 de .00558 -.01143 .00519 fl .64175 .59593 -.56060 ga .03171 .06426 -.09120 Number of cases read: 10 Number of cases listed: 10
VARIABLE LABLES sdfb1 "Sdfbeta pctmetro"
/sdfb2 "Sdfbeta poverty"
/sdfb3 "Sdfbeta single" .
GRAPH
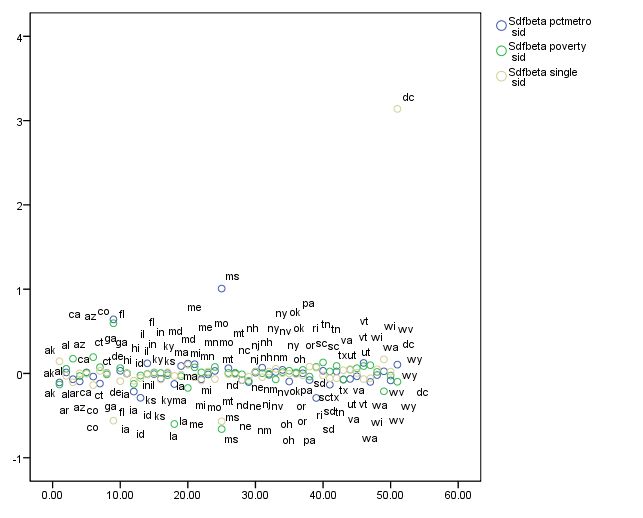
/SCATTERPLOT(OVERLAY)=sid sid sid WITH sdfb1 sdfb2 sdfb3 (PAIR) BY state(name)
/MISSING=LISTWISE .
| Note | |
| Measure | Value |
| leverage | >(2k+2)/n |
| abs(rstu) | > 2 |
| Cook's D | > 4/n |
| abs(DFBETA) | > 2/sqrt(n) |
PRED Unstandardized predicted values. RESID Unstandardized residuals. DRESID Deleted residuals. ADJPRED Adjusted predicted values. ZPRED Standardized predicted values. ZRESID Standardized residuals. SRESID Studentized residuals. SDRESID Studentized deleted residuals. SEPRED Standard errors of the predicted values. MAHAL Mahalanobis distances. COOK Cook’s distances. LEVER Centered leverage values. DFBETA Change in the regression coefficient that results from the deletion of the ith case. A DFBETA value is computed for each case for each regression coefficient generated by a model. SDBETA Standardized DFBETA. An SDBETA value is computed for each case for each regression coefficient generated by a model. DFFIT Change in the predicted value when the ith case is deleted. SDFIT Standardized DFFIT. COVRATIO Ratio of the determinant of the covariance matrix with the ith case deleted to the determinant of the covariance matrix with all cases included. MCIN Lower and upper bounds for the prediction interval of the mean predicted response. A lowerbound LMCIN and an upperbound UMCIN are generated. The default confidence interval is 95%. The confidence interval can be reset with the CIN subcommand. (See Dillon & Goldstein ICIN Lower and upper bounds for the prediction interval for a single observation. A lowerbound LICIN and an upperbound UICIN are generated. The default confidence interval is 95%. The confidence interval can be reset with the CIN subcommand. (See Dillon & Goldstein
regression /dependent crime /method=enter pctmetro poverty single /residuals=histogram(sdresid lever) id(state) outliers(sdresid, lever, cook) /casewise=plot(sdresid) outliers(2) cook dffit /scatterplot(*lever, *sdresid) /partialplot.
regression /dependent crime /method=enter pctmetro poverty single.
Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) -1666.436 147.852 -11.271 .000 pct metropolitan 7.829 1.255 .390 6.240 .000 pct poverty 17.680 6.941 .184 2.547 .014 pct single parent 132.408 15.503 .637 8.541 .000 a. Dependent Variable: violent crime rate
compute filtvar = (state NE "dc"). filter by filtvar. regression /dependent crime /method=enter pctmetro poverty single .
Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) -1197.538 180.487 -6.635 .000 pct metropolitan 7.712 1.109 .565 6.953 .000 pct poverty 18.283 6.136 .265 2.980 .005 pct single parent 89.401 17.836 .446 5.012 .000 a. Dependent Variable: violent crime rate
e.g., 2
inspection
descriptives /var= ALL .
| Descriptive Statistics | ||||||
| N | Minimum | Maximum | Mean | Std. Deviation | ||
| api 2000 | 400 | 369 | 940 | 647.62 | 142.249 | |
| english language learners | 400 | 0 | 91 | 31.45 | 24.839 | |
| avg class size k-3 | 398 | 14 | 25 | 19.16 | 1.369 | |
| avg parent ed | 381 | 1.00 | 4.62 | 2.6685 | .76379 | |
| pct free meals | 400 | 0 | 100 | 60.32 | 31.912 | |
| Valid N (listwise) | 379 | |||||
graph /scatterplot(matrix)=api00 ell acs_k3 avg_ed meals .
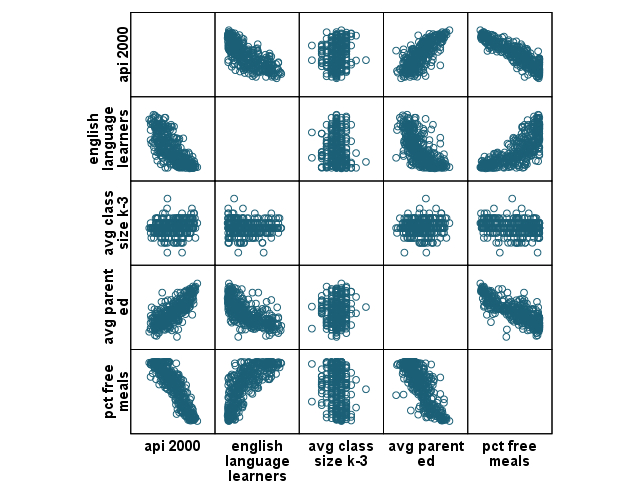
This graph does not give any suspicious cases.
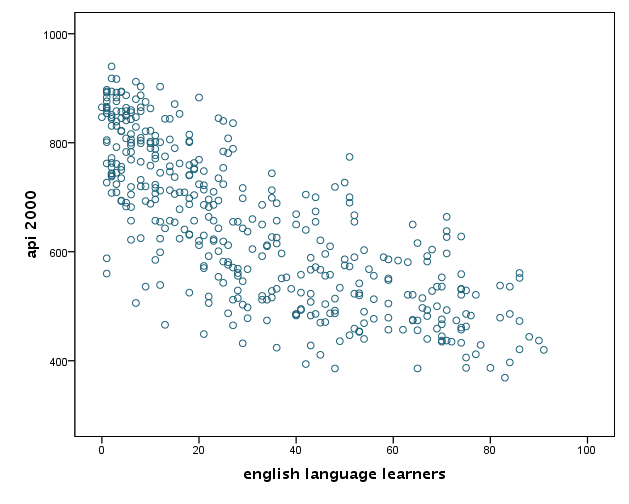
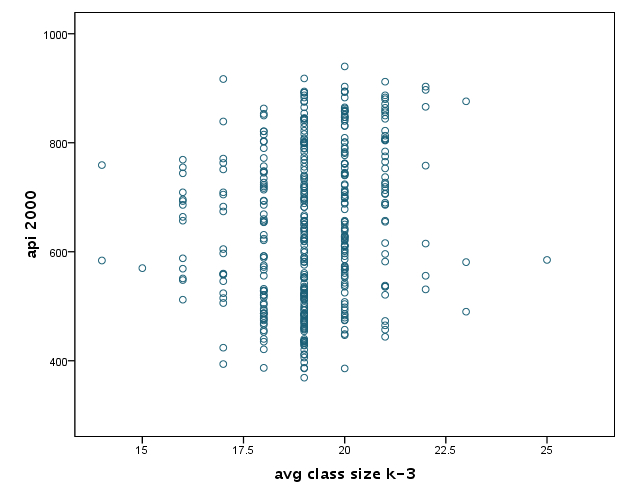
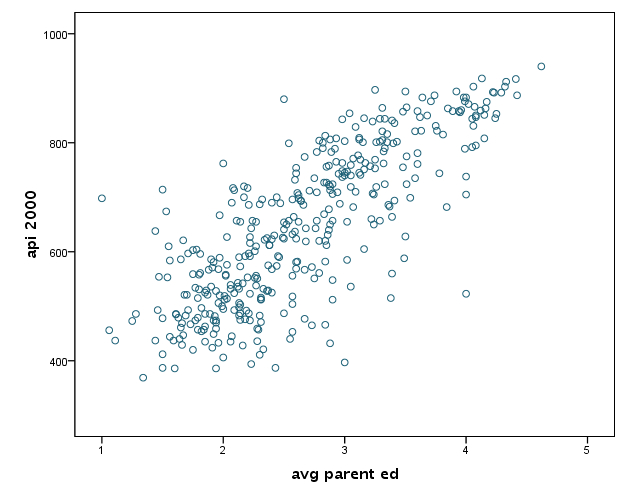
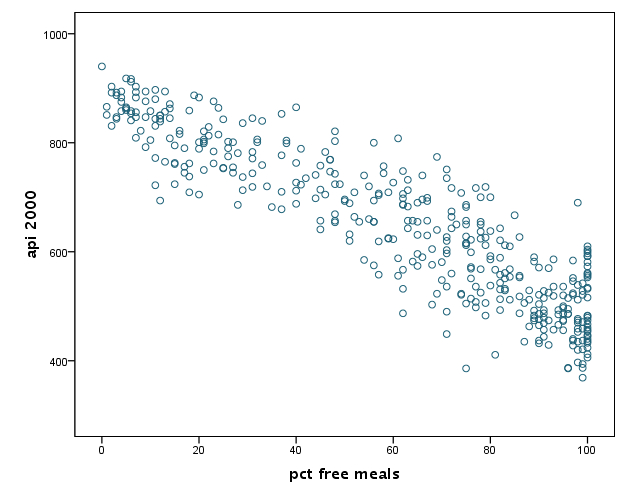
GRAPH /SCATTERPLOT(BIVAR)=ell with api00 . GRAPH /SCATTERPLOT(BIVAR)=acs_k3 with api00 . GRAPH /SCATTERPLOT(BIVAR)=avg_ed with api00 . GRAPH /SCATTERPLOT(BIVAR)=meals with api00 .
We speculate that the second IV (average class size) is not quite related to DV (api00). And, there seems no particular suspicious data.
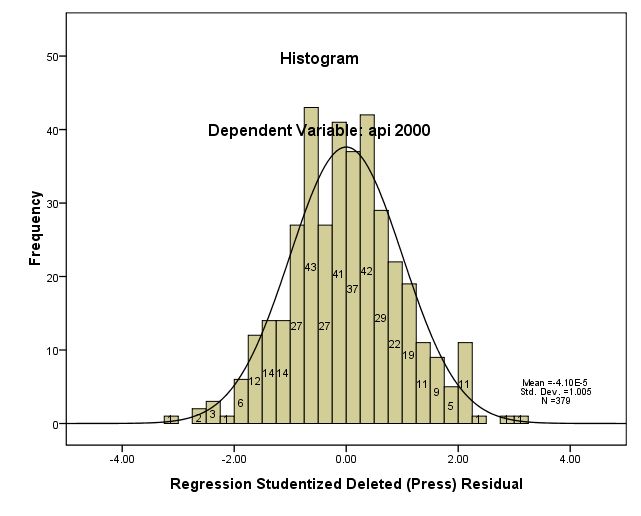
REGRESSION /DEPENDENT api00 /METHOD=ENTER ell acs_k3 avg_ed meals /residuals=histogram(sdresid lever) id(snum) outliers(sdresid, lever, cook) /casewise=plot(sdresid) outliers(2) cook dffit /scatterplot(*lever, *sdresid) /save sdbeta(sdfb) /partialplot.
| Model Summary | ||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | .912a | .833 | .831 | 58.633 |
| a. Predictors: (Constant), pct free meals, avg class size k-3, english language learners, avg parent ed | ||||
| ANOVA(b) | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 6393719.254 | 4 | 1598429.813 | 464.956 | .000a |
| Residual | 1285740.498 | 374 | 3437.809 | |||
| Total | 7679459.752 | 378 | ||||
| a. Predictors: (Constant), pct free meals, avg class size k-3, english language learners, avg parent ed | ||||||
| b. Dependent Variable: api 2000 | ||||||
| Coefficients(a) | ||||||
| Unstandardized Coefficients | Standardized Coefficients | |||||
| Model | B | Std. Error | Beta | t | Sig. | |
| 1 | (Constant) | 709.639 | 56.240 | 12.618 | .000 | |
| english language learners | -.843 | .196 | -.147 | -4.307 | .000 | |
| avg class size k-3 | 3.388 | 2.333 | .032 | 1.452 | .147 | |
| avg parent ed | 29.072 | 6.924 | .156 | 4.199 | .000 | |
| pct free meals | -2.937 | .195 | -.655 | -15.081 | .000 | |
| a. Dependent Variable: api 2000 | ||||||
| Casewise Diagnostics(a) | |||||
| Case Number | school number | Stud. Deleted Residual | api 2000 | Cook's Distance | DFFIT |
| 93 | 1497 | 2.170 | 604 | .010 | 1.292 |
| 97 | 1539 | 2.230 | 700 | .006 | .826 |
| 100 | 1515 | 2.222 | 667 | .005 | .661 |
| 105 | 1516 | 2.128 | 597 | .010 | 1.380 |
| 135 | 1633 | 2.072 | 584 | .044 | 6.085 |
| 188 | 1731 | 2.121 | 719 | .015 | 2.126 |
| 203 | 1621 | 2.034 | 717 | .006 | .831 |
| 226 | 211 | -3.241 | 386 | .015 | -1.325 |
| 227 | 182 | -2.653 | 411 | .005 | -.581 |
| 228 | 167 | 2.903 | 774 | .010 | .987 |
| 232 | 210 | -2.369 | 432 | .018 | -2.263 |
| 234 | 165 | -2.734 | 449 | .019 | -1.997 |
| 252 | 3700 | 2.036 | 717 | .013 | 1.878 |
| 259 | 3537 | -2.425 | 694 | .012 | -1.436 |
| 271 | 3758 | 3.012 | 690 | .022 | 2.108 |
| 272 | 3794 | 2.083 | 610 | .010 | 1.400 |
| 274 | 3759 | -2.290 | 585 | .069 | -8.646 |
| 304 | 4507 | 2.011 | 751 | .013 | 1.917 |
| 327 | 4737 | 2.470 | 808 | .012 | 1.447 |
| 334 | 4744 | 2.160 | 700 | .005 | .645 |
| 346 | 5362 | -2.138 | 487 | .010 | -1.359 |
| a. Dependent Variable: api 2000 | |||||
| Residuals Statistics(a) | |||||
| Minimum | Maximum | Mean | Std. Deviation | N | |
| Predicted Value | 449.17 | 910.04 | 647.64 | 130.056 | 379 |
| Std. Predicted Value | -1.526 | 2.018 | .000 | 1.000 | 379 |
| Standard Error of Predicted Value | 3.218 | 14.681 | 6.496 | 1.780 | 379 |
| Adjusted Predicted Value | 449.44 | 909.36 | 647.65 | 130.056 | 379 |
| Residual | -187.020 | 173.697 | .000 | 58.322 | 379 |
| Std. Residual | -3.190 | 2.962 | .000 | .995 | 379 |
| Stud. Residual | -3.201 | 2.980 | .000 | 1.002 | 379 |
| Deleted Residual | -188.345 | 175.805 | -.016 | 59.138 | 379 |
| Stud. Deleted Residual | -3.241 | 3.012 | .000 | 1.005 | 379 |
| Mahal. Distance | .141 | 22.702 | 3.989 | 3.030 | 379 |
| Cook's Distance | .000 | .069 | .003 | .006 | 379 |
| Centered Leverage Value | .000 | .060 | .011 | .008 | 379 |
| a. Dependent Variable: api 2000 | |||||
| Outlier Statistics(a) | |||||
| Case Number | school number | Statistic | Sig. F | ||
| Stud. Deleted Residual | 1 | 226 | 211 | -3.241 | |
| 2 | 271 | 3758 | 3.012 | ||
| 3 | 228 | 167 | 2.903 | ||
| 4 | 234 | 165 | -2.734 | ||
| 5 | 227 | 182 | -2.653 | ||
| 6 | 327 | 4737 | 2.470 | ||
| 7 | 259 | 3537 | -2.425 | ||
| 8 | 232 | 210 | -2.369 | ||
| 9 | 274 | 3759 | -2.290 | ||
| 10 | 97 | 1539 | 2.230 | ||
| Cook's Distance | 1 | 274 | 3759 | .069 | .997 |
| 2 | 135 | 1633 | .044 | .999 | |
| 3 | 26 | 4299 | .030 | 1.000 | |
| 4 | 193 | 1952 | .025 | 1.000 | |
| 5 | 271 | 3758 | .022 | 1.000 | |
| 6 | 234 | 165 | .019 | 1.000 | |
| 7 | 232 | 210 | .018 | 1.000 | |
| 8 | 200 | 1872 | .018 | 1.000 | |
| 9 | 108 | 1606 | .018 | 1.000 | |
| 10 | 388 | 4878 | .017 | 1.000 | |
| Centered Leverage Value | 1 | 274 | 3759 | .060 | |
| 2 | 37 | 4308 | .058 | ||
| 3 | 209 | 1795 | .050 | ||
| 4 | 135 | 1633 | .046 | ||
| 5 | 26 | 4299 | .040 | ||
| 6 | 69 | 3000 | .037 | ||
| 7 | 372 | 6068 | .036 | ||
| 8 | 30 | 4317 | .035 | ||
| 9 | 147 | 1709 | .035 | ||
| 10 | 193 | 1952 | .033 | ||
| a. Dependent Variable: api 2000 | |||||
Outlier dection
Let's say, we decide to opt out cases whose studentized deleted residual value exceed normal. We set the criterion as ABS(sdresid) > 2. These cases which meet this criterion will filtered out.
We need to save some residual statistics first, with regression method. Saved values include:
PRED
ZPRED
MAHAL
COOK
LEVER
RESID
ZRESID
SDRESID
DFBETA
Among them, we take a look at SDRESID, whose variable name will be SDR_1 in spss data set.
For the referece,
| Note: outlier detection | ||
| Measure | Value | |
| leverage | >(2k+2)/n | 0.021108179 |
| abs(rstu) | > 2 | 2 |
| Cook's D | > 4/n | 0.01055409 |
| abs(DFBETA) | > 2/sqrt(n) | 0.102733099 |
REGRESSION /DESCRIPTIVES MEAN STDDEV CORR SIG N /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA COLLIN TOL CHANGE ZPP /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN /DEPENDENT api00 /METHOD=ENTER meals ell acs_k3 avg_ed /residuals=histogram(sdresid lever) id(snum) outliers(sdresid, lever, cook) Durbin /casewise=plot(sdresid) outliers(2) cook dffit /SCATTERPLOT=(*ZRESID ,*ZPRED) /SAVE PRED ZPRED MAHAL COOK LEVER RESID ZRESID SDRESID DFBETA.
Then, we need to filter out cases whose SDR_1 value exceed:
abs(SDR_1) > 2
with the below command.
USE ALL. COMPUTE filterVar=(abs(SDR)_1 < 2). FILTER BY filterVar. EXECUTE.
Then, we do regression again, excluding the suspicious cases. But, this time we do not save the residuals.
REGRESSION /DESCRIPTIVES MEAN STDDEV CORR SIG N /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA CHANGE ZPP /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN /DEPENDENT api00 /METHOD=ENTER ell avg_ed acs_k3 meals /SCATTERPLOT=(*ZRESID ,*ZPRED) .
Compare the ouptput between the previous and this regression.
| Model Summaryb | |||||||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate | Change Statistics | ||||
| R Square Change | F Change | df1 | df2 | Sig. F Change | |||||
| 1 | .938a | .880 | .879 | 49.914 | .880 | 649.458 | 4 | 353 | .000 |
| ANOVAb | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 6472284.822 | 4 | 1618071.206 | 649.458 | .000a |
| Residual | 879470.664 | 353 | 2491.418 | |||
| Total | 7351755.486 | 357 | ||||
| Coefficientsa | |||||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | Correlations | ||||
| B | Std. Error | Beta | Zero-order | Partial | Part | ||||
| 1 | (Constant) | 705.495 | 51.072 | 13.814 | .000 | ||||
| ell | -.915 | .170 | -.160 | -5.374 | .000 | -.789 | -.275 | -.099 | |
| avg_ed | 25.661 | 6.061 | .138 | 4.234 | .000 | .809 | .220 | .078 | |
| acs_k3 | 4.452 | 2.127 | .040 | 2.093 | .037 | .204 | .111 | .039 | |
| meals | -3.056 | .171 | -.683 | -17.868 | .000 | -.928 | -.689 | -.329 | |