Table of Contents
Multiple Regression
data file
University of New Mexico enrollment data (for 30 years)
ROLL: # of enrollment
UNEM: enemployment level
HGRAD: # of High school graduates
INC: income level
# data import
> datavar <- read.csv("http://commres.net/wiki/_media/r/dataset_hlr.csv")
> str(datavar)
'data.frame': 29 obs. of 5 variables:
$ YEAR : int 1 2 3 4 5 6 7 8 9 10 ...
$ ROLL : int 5501 5945 6629 7556 8716 9369 9920 10167 11084 12504 ...
$ UNEM : num 8.1 7 7.3 7.5 7 6.4 6.5 6.4 6.3 7.7 ...
$ HGRAD: int 9552 9680 9731 11666 14675 15265 15484 15723 16501 16890 ...
$ INC : int 1923 1961 1979 2030 2112 2192 2235 2351 2411 2475 ...
>
two.predictor.model <- lm(ROLL ~ UNEM + HGRAD, datavar) summary(two.predictor.model) two.predictor.model
three.predictor.model <- lm(ROLL ~ UNEM + HGRAD + INC, datavar) summary(three.predictor.model) three.predictor.model
> two.predictor.model <- lm(ROLL ~ UNEM + HGRAD, datavar)
> summary(two.predictor.model)
Call:
lm(formula = ROLL ~ UNEM + HGRAD, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-2102.2 -861.6 -349.4 374.5 3603.5
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.256e+03 2.052e+03 -4.023 0.00044 ***
UNEM 6.983e+02 2.244e+02 3.111 0.00449 **
HGRAD 9.423e-01 8.613e-02 10.941 3.16e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1313 on 26 degrees of freedom
Multiple R-squared: 0.8489, Adjusted R-squared: 0.8373
F-statistic: 73.03 on 2 and 26 DF, p-value: 2.144e-11
> two.predictor.model
Call:
lm(formula = ROLL ~ UNEM + HGRAD, data = datavar)
Coefficients:
(Intercept) UNEM HGRAD
-8255.7511 698.2681 0.9423
>
> three.predictor.model <- lm(ROLL ~ UNEM + HGRAD + INC, datavar)
> summary(three.predictor.model)
Call:
lm(formula = ROLL ~ UNEM + HGRAD + INC, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-1148.84 -489.71 -1.88 387.40 1425.75
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -9.153e+03 1.053e+03 -8.691 5.02e-09 ***
UNEM 4.501e+02 1.182e+02 3.809 0.000807 ***
HGRAD 4.065e-01 7.602e-02 5.347 1.52e-05 ***
INC 4.275e+00 4.947e-01 8.642 5.59e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 670.4 on 25 degrees of freedom
Multiple R-squared: 0.9621, Adjusted R-squared: 0.9576
F-statistic: 211.5 on 3 and 25 DF, p-value: < 2.2e-16
> three.predictor.model
Call:
lm(formula = ROLL ~ UNEM + HGRAD + INC, data = datavar)
Coefficients:
(Intercept) UNEM HGRAD INC
-9153.2545 450.1245 0.4065 4.2749
>
만약에
- unemployment rate (UNEM) = 9%, 12%, 3%
- spring high school graduating class (HGRAD) = 100000, 98000, 78000
- a per capita income (INC) of \$30000, \$28000, \$36000
- 일 때, enrollment는 어떻게 predict할 수 있을까?
위에서 얻은 prediction model은 아래와 같다.
$$ \hat{Y} = -9153.2545 + 450.1245 \cdot UNEM + 0.4065 \cdot HGRAD + 4.2749 \cdot INC $$
여기에 위의 정보를 대입해 보면 된다.
new.data <- data.frame(UNEM=c(9, 12, 3), HGRAD=c(100000, 98000, 78000), INC=c(30000, 28000, 36000)) predict(three.predictor.model, newdata=new.data)
> new.data <- data.frame(UNEM=c(9, 10, 15), HGRAD=c(100000, 98000, 78000), INC=c(30000, 28000, 19000))
> predict(three.predictor.model, newdata=new.data)
1 2 3
163792.0 154879.4 110526.6
>
\begin{align*} \hat{Y} & = -9153.2545 + 450.1245 \cdot \text{UNEM} + 0.4065 \cdot \text{HGRAD} + 4.2749 \cdot \text{INC} \\ 163792.0 & = -9153.2545 + 450.1245 \cdot (9) + 0.4065 \cdot (100000) + 4.2749 \cdot (30000) \\ 154879.4 & = -9153.2545 + 450.1245 \cdot (10) + 0.4065 \cdot (98000) + 4.2749 \cdot (28000) \\ 110526.6 & = -9153.2545 + 450.1245 \cdot (15) + 0.4065 \cdot (78000) + 4.2749 \cdot (19000) \\ \end{align*}
beta coefficient 살펴보기
see beta coefficients
# install.packages('lm.beta')
# library(lm.beta)
lm.beta(three.predictor.model)
> # install.packages('lm.beta')
> # library(lm.beta)
> lm.beta(three.predictor.model)
Call:
lm(formula = ROLL ~ UNEM + HGRAD + INC, data = datavar)
Standardized Coefficients::
(Intercept) UNEM HGRAD INC
0.0000000 0.1553619 0.3656177 0.6061762
>
by hand
# coefficient * (sd(x)/sd(y)) 이므로 # attach(datavar) sd.roll <- sd(ROLL) sd.unem <- sd(UNEM) sd.hgrad <- sd(HGRAD) sd.inc <- sd(INC) b.unem <- three.predictor.model$coefficients[2] b.hgrad <- three.predictor.model$coefficients[3] b.inc <- three.predictor.model$coefficients[4] ## or b.unem <- 4.501e+02 b.hgrad <- 4.065e-01 b.inc <- 4.275e+00 b.unem * (sd.unem / sd.roll) b.hgrad * (sd.hgrad / sd.roll) b.inc * (sd.inc / sd.roll) lm.beta(three.predictor.model)
output of the above
> sd.roll <- sd(ROLL)
> sd.unem <- sd(UNEM)
> sd.hgrad <- sd(HGRAD)
> sd.inc <- sd(INC)
>
> b.unem <- three.predictor.model$coefficients[2]
> b.hgrad <- three.predictor.model$coefficients[3]
> b.inc <- three.predictor.model$coefficients[4]
>
> ## or
> b.unem <- 4.501e+02
> b.hgrad <- 4.065e-01
> b.inc <- 4.275e+00
>
>
> b.unem * (sd.unem / sd.roll)
[1] 0.1554
> b.hgrad * (sd.hgrad / sd.roll)
[1] 0.3656
> b.inc * (sd.inc / sd.roll)
[1] 0.6062
>
> lm.beta(three.predictor.model)
Call:
lm(formula = ROLL ~ UNEM + HGRAD + INC, data = datavar)
Standardized Coefficients::
(Intercept) UNEM HGRAD INC
0.0000 0.1554 0.3656 0.6062
>
see also Sequential method regression modeling by hand
see also statistical regression methods regression modeling by computing
> fit <- three.predictor.model
> step <- stepAIC(fit, direction="both")
Start: AIC=381.2
ROLL ~ UNEM + HGRAD + INC
Df Sum of Sq RSS AIC
<none> 11237313 381
- UNEM 1 6522098 17759411 392
- HGRAD 1 12852039 24089352 401
- INC 1 33568255 44805568 419
>
Housing
e.g.
etc
marketing <- read.csv("http://commres.net/wiki/_media/marketing_from_datarium.csv")
# install.packages("tidyverse", dep=TRUE)
library(tidyverse)
data("marketing", package = "datarium")
head(marketing, 4)
- Data, marketing is the impact of the amount of money spent on three advertising medias (youtube, facebook and newspaper) on sales.
- Note that to list all the independent (explanatory) variables, you could use
lm (sales ~ ., data=“marketing”). - You could also use
-sign to subtract ivs.lm(sales ~ . - newspapers, data = “marketing”)
mod <- lm(sales ~ . , data=marketing) summary(mod) summary(mod)$coefficients
mod2 <- lm(sales ~ . - newspaper, data = marketing) summary(mod2)
> mod <- lm(sales ~ . , data=marketing)
> summary(mod)
Call:
lm(formula = sales ~ ., data = marketing)
Residuals:
Min 1Q Median 3Q Max
-10.5932 -1.0690 0.2902 1.4272 3.3951
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.526667 0.374290 9.422 <2e-16 ***
youtube 0.045765 0.001395 32.809 <2e-16 ***
facebook 0.188530 0.008611 21.893 <2e-16 ***
newspaper -0.001037 0.005871 -0.177 0.86
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.023 on 196 degrees of freedom
Multiple R-squared: 0.8972, Adjusted R-squared: 0.8956
F-statistic: 570.3 on 3 and 196 DF, p-value: < 2.2e-16
> summary(mod)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.526667243 0.374289884 9.4222884 1.267295e-17
youtube 0.045764645 0.001394897 32.8086244 1.509960e-81
facebook 0.188530017 0.008611234 21.8934961 1.505339e-54
newspaper -0.001037493 0.005871010 -0.1767146 8.599151e-01
> mod2 <- lm(sales ~ . - newspaper, data = marketing)
> summary(mod2)
Call:
lm(formula = sales ~ . - newspaper, data = marketing)
Residuals:
Min 1Q Median 3Q Max
-10.5572 -1.0502 0.2906 1.4049 3.3994
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.50532 0.35339 9.919 <2e-16 ***
youtube 0.04575 0.00139 32.909 <2e-16 ***
facebook 0.18799 0.00804 23.382 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.018 on 197 degrees of freedom
Multiple R-squared: 0.8972, Adjusted R-squared: 0.8962
F-statistic: 859.6 on 2 and 197 DF, p-value: < 2.2e-16
sales = 3.5 + 0.045*youtube + 0.187*facebook.
Prediction
Predict(lm.fit, newdata=data.frame(x1=c(2,3,4), x2=c(3,3,3))
Year <- c(2017, 2017, 2017, 2017, 2017, 2017, 2017,
2017, 2017, 2017, 2017, 2017, 2016, 2016,
2016, 2016, 2016, 2016, 2016, 2016, 2016,
2016, 2016, 2016)
Month <- c(12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1,
12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1)
Interest_Rate <- c(2.75, 2.5, 2.5, 2.5, 2.5, 2.5,
2.5, 2.25, 2.25, 2.25, 2, 2, 2, 1.75,
1.75, 1.75, 1.75, 1.75, 1.75, 1.75,
1.75, 1.75, 1.75, 1.75)
Unemployment_Rate <- c(5.3, 5.3, 5.3, 5.3, 5.4, 5.6,
5.5, 5.5, 5.5, 5.6, 5.7, 5.9, 6, 5.9,
5.8, 6.1, 6.2, 6.1, 6.1, 6.1, 5.9, 6.2,
6.2, 6.1)
Stock_Index_Price <- c(1464, 1394, 1357, 1293, 1256,
1254, 1234, 1195, 1159, 1167, 1130, 1075,
1047, 965, 943, 958, 971, 949, 884, 866,
876, 822, 704, 719)
dat.stock <- data.frame(Year, Month, Interest_Rate, Unemployment_Rate, Stock_Index_Price) dat.stock Year Month Interest_Rate Unemployment_Rate Stock_Index_Price 1 2017 12 2.75 5.3 1464 2 2017 11 2.50 5.3 1394 3 2017 10 2.50 5.3 1357 4 2017 9 2.50 5.3 1293 5 2017 8 2.50 5.4 1256 6 2017 7 2.50 5.6 1254 7 2017 6 2.50 5.5 1234 8 2017 5 2.25 5.5 1195 9 2017 4 2.25 5.5 1159 10 2017 3 2.25 5.6 1167 11 2017 2 2.00 5.7 1130 12 2017 1 2.00 5.9 1075 13 2016 12 2.00 6.0 1047 14 2016 11 1.75 5.9 965 15 2016 10 1.75 5.8 943 16 2016 9 1.75 6.1 958 17 2016 8 1.75 6.2 971 18 2016 7 1.75 6.1 949 19 2016 6 1.75 6.1 884 20 2016 5 1.75 6.1 866 21 2016 4 1.75 5.9 876 22 2016 3 1.75 6.2 822 23 2016 2 1.75 6.2 704 24 2016 1 1.75 6.1 719 >
lm.stock <- lm(Stock_Index_Price~Interest_Rate+Unemployment_Rate, data=dat.stock) summary(lm.stock) lm.stock$coefficient coefficients(lm.stock)
> names(lm.stock) [1] "coefficients" "residuals" "effects" "rank" "fitted.values" [6] "assign" "qr" "df.residual" "xlevels" "call" [11] "terms" "model"
> lm.stock <- lm(Stock_Index_Price~Interest_Rate+Unemployment_Rate, data=dat.stock)
> summary(lm.stock)
Call:
lm(formula = Stock_Index_Price ~ Interest_Rate + Unemployment_Rate,
data = dat.stock)
Residuals:
Min 1Q Median 3Q Max
-158.205 -41.667 -6.248 57.741 118.810
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1798.4 899.2 2.000 0.05861 .
Interest_Rate 345.5 111.4 3.103 0.00539 **
Unemployment_Rate -250.1 117.9 -2.121 0.04601 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 70.56 on 21 degrees of freedom
Multiple R-squared: 0.8976, Adjusted R-squared: 0.8879
F-statistic: 92.07 on 2 and 21 DF, p-value: 4.043e-11
> lm.stock$coefficient
(Intercept) Interest_Rate Unemployment_Rate
1798.4040 345.5401 -250.1466
> coefficients(lm.stock)
(Intercept) Interest_Rate Unemployment_Rate
1798.4040 345.5401 -250.1466
>
>
dat.stock.new.iv <- data.frame(Interest_Rate=c(5,6,2,1), Unemployment_Rate=c(8,8.5,4,3)) predict(lm.stock, newdata=dat.stock.new.iv)
> dat.stock.new.iv <- data.frame(Interest_Rate=c(5,6,2,1), Unemployment_Rate=c(8,8.5,4,3))
> predict(lm.stock, newdata=dat.stock.new.iv)
1 2 3 4
1524.932 1745.399 1488.898 1393.504
>
Partial, Semi-partial Correlation and R squared value
아래에서, summary(lm.stock)은
> lm.stock <- lm(Stock_Index_Price~Interest_Rate+Unemployment_Rate, data=dat.stock)
> summary(lm.stock)
Call:
lm(formula = Stock_Index_Price ~ Interest_Rate + Unemployment_Rate,
data = dat.stock)
Residuals:
Min 1Q Median 3Q Max
-158.205 -41.667 -6.248 57.741 118.810
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1798.4 899.2 2.000 0.05861 .
Interest_Rate 345.5 111.4 3.103 0.00539 **
Unemployment_Rate -250.1 117.9 -2.121 0.04601 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 70.56 on 21 degrees of freedom
Multiple R-squared: 0.8976, Adjusted R-squared: 0.8879
F-statistic: 92.07 on 2 and 21 DF, p-value: 4.043e-11
>
> anova(lm.stock)
Analysis of Variance Table
Response: Stock_Index_Price
Df Sum Sq Mean Sq F value Pr(>F)
Interest_Rate 1 894463 894463 179.6477 9.231e-12 ***
Unemployment_Rate 1 22394 22394 4.4977 0.04601 *
Residuals 21 104559 4979
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
| df | SS | ms | F | |
| interest | 1 (a) | 894463 (1) | 894463 | 179.6471179 |
| unemp | 1 (b) | 22394 (2) | 22394 | 4.497690299 |
| res | 21 (c) | 104559 (3) | 4979 | |
| total | 23 | 1021416 (4) | ||
| interest + enemp | 916857 (5) |
(4) = (1) + (2) + (3)
(5) = (1) + (2)
from the above summary(lm.stock)
Multiple R-squared: 0.8976, . . . .
F-statistic: 92.07 on 2 and 21 DF, p-value: 4.043e-11
\begin{eqnarray*} R^2 & = & \dfrac {SS_{reg}}{SS_{total}} \\ & = & \dfrac{(5)}{(4)}, \qquad \text{from the table} \\ & = & \dfrac {916857}{1021416} \\ & = & 0.897633286 \\ & = & 0.8976 \end{eqnarray*}
\begin{eqnarray*} F & = & \dfrac {MS_{reg}} {MS_{res}} \\ & = & \dfrac {(5)/(a)+(b)}{(3)/(c)} \\ & = & \dfrac {916857/2}{104559/21} \\ & = & 92.0724041 \\ & = & 92.07 \qquad (df = 2, 21) \end{eqnarray*}
그런데, 각각의 IV와 DV 간의 correlation 값은:
> cor.test(Stock_Index_Price, Interest_Rate)
Pearson's product-moment correlation
data: Stock_Index_Price and Interest_Rate
t = 12.45, df = 22, p-value = 1.954e-11
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8552498 0.9721916
sample estimates:
cor
0.9357932
> cor.test(Stock_Index_Price, Unemployment_Rate)
Pearson's product-moment correlation
data: Stock_Index_Price and Unemployment_Rate
t = -11.196, df = 22, p-value = 1.487e-10
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.9662308 -0.8264284
sample estimates:
cor
-0.9223376
>
Stock_Index_Price ~ Interest_Rate = 0.9357932
Stock_Index_Price ~ Unemployment_Rate = -0.9223376
각각의 r square 값은
Stock_Index_Price ~ Interest_Rate -> 0.875708913
Stock_Index_Price ~ Unemployment_Rate -> 0.850706648
이 둘의 합은 1.726415562 로 1을 넘는다. 즉, 각 독립변인의 영향력은 중복 (독립변인 간의 상관관계) 되어 있다는 뜻.
install.packages("ppcor")
library(ppcor)
> pcor.test(Stock_Index_Price, Interest_Rate, Unemployment_Rate) estimate p.value statistic n gp Method 1 0.560649 0.005389174 3.102717 24 1 pearson
> spcor.test(Stock_Index_Price, Interest_Rate, Unemployment_Rate) estimate p.value statistic n gp Method 1 0.2166264 0.3207966 1.016852 24 1 pearson
0.2166264^2 = 0.046926997
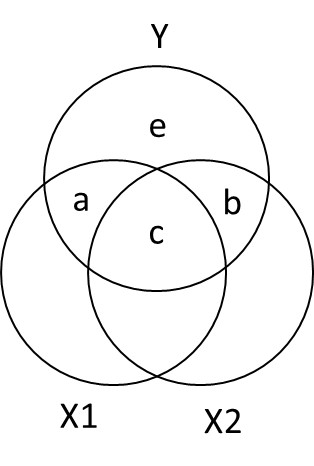
b + c / a + b + c + d = 0.8757
b / a + b + c + d = 0.0467
c / a + b + c + d = 0.8288
> spcor.test(Stock_Index_Price, Unemployment_Rate, Interest_Rate)
estimate p.value statistic n gp Method
1 -0.1480697 0.5001535 -0.6861036 24 1 pearson
>
(-0.1480697)^2 = 0.021924636 = 0.0219
d + c / a + b + c + d = 0.8507
d / a + b + c + d = 0.0219
c / a + b + c + d = 0.8288
위와 아래의 c / a + b + c + d = 0.8288 가 일치하므로, 독립변인 둘의 겹치는 영향력이 크다는 것을 알수 있다.
> lm.stock.int <- lm(Stock_Index_Price~Interest_Rate, data=dat.stock)
> summary(lm.stock.int)
Call:
lm(formula = Stock_Index_Price ~ Interest_Rate, data = dat.stock)
Residuals:
Min 1Q Median 3Q Max
-183.892 -30.181 4.455 56.608 101.057
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -99.46 95.21 -1.045 0.308
Interest_Rate 564.20 45.32 12.450 1.95e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 75.96 on 22 degrees of freedom
Multiple R-squared: 0.8757, Adjusted R-squared: 0.8701
F-statistic: 155 on 1 and 22 DF, p-value: 1.954e-11
> lm.stock.unemp <- lm(Stock_Index_Price ~ Unemployment_Rate, data=dat.stock)
> summary(lm.stock.unemp)
Call:
lm(formula = Stock_Index_Price ~ Unemployment_Rate, data = dat.stock)
Residuals:
Min 1Q Median 3Q Max
-159.671 -41.996 2.089 72.381 151.226
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4471.3 304.2 14.7 7.41e-13 ***
Unemployment_Rate -589.0 52.6 -11.2 1.49e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 83.25 on 22 degrees of freedom
Multiple R-squared: 0.8507, Adjusted R-squared: 0.8439
F-statistic: 125.4 on 1 and 22 DF, p-value: 1.487e-10
>
>
> anova(lm.stock.int, lm.stock) Analysis of Variance Table Model 1: Stock_Index_Price ~ Interest_Rate Model 2: Stock_Index_Price ~ Interest_Rate + Unemployment_Rate Res.Df RSS Df Sum of Sq F Pr(>F) 1 22 126953 2 21 104559 1 22394 4.4977 0.04601 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> anova(lm.stock.unemp, lm.stock) Analysis of Variance Table Model 1: Stock_Index_Price ~ Unemployment_Rate Model 2: Stock_Index_Price ~ Interest_Rate + Unemployment_Rate Res.Df RSS Df Sum of Sq F Pr(>F) 1 22 152491 2 21 104559 1 47932 9.6269 0.005389 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 >
Alternatively,
> install.packages("lmtest")
> library(lmtest)
> lrtest(lm.stock.int, lm.stock)
Likelihood ratio test
Model 1: Stock_Index_Price ~ Interest_Rate
Model 2: Stock_Index_Price ~ Interest_Rate + Unemployment_Rate
#Df LogLik Df Chisq Pr(>Chisq)
1 3 -136.94
2 4 -134.61 1 4.6576 0.03092 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
e.g. 5
http://www.alexanderdemos.org/Class2.html
#packages we will need to conduct to create and graph our data
library(MASS) #create data
library(car) #graph data
py1 =.6 #Cor between X1 (Practice Time) and Memory Errors
py2 =.4 #Cor between X2 (Performance Anxiety) and Memory Errors
p12= .3 #Cor between X1 (Practice Time) and X2 (Performance Anxiety)
Means.X1X2Y<- c(10,10,10) #set the means of X and Y variables
CovMatrix.X1X2Y <- matrix(c(1,p12,py1,
p12,1,py2,
py1,py2,1),3,3) # creates the covariate matrix
#build the correlated variables. Note: empirical=TRUE means make the correlation EXACTLY r.
# if we say empirical=FALSE, the correlation would be normally distributed around r
set.seed(42)
CorrDataT<-mvrnorm(n=100, mu=Means.X1X2Y,Sigma=CovMatrix.X1X2Y, empirical=TRUE)
#Convert them to a "Data.Frame" & add our labels to the vectors we created
CorrDataT<-as.data.frame(CorrDataT)
colnames(CorrDataT) <- c("Practice","Anxiety","Memory")
#make the scatter plots
scatterplot(Memory~Practice,CorrDataT)
scatterplot(Memory~Anxiety,CorrDataT)
scatterplot(Anxiety~Practice,CorrDataT)
# Pearson Correlations
ry1<-cor(CorrDataT$Memory,CorrDataT$Practice)
ry2<-cor(CorrDataT$Memory,CorrDataT$Anxiety)
r12<-cor(CorrDataT$Anxiety,CorrDataT$Practice)
ry1 ry2 r12 ry1^2 ry2^2 r12^2
> ry1 [1] 0.6 > ry2 [1] 0.4 > r12 [1] 0.3 > > ry1^2 [1] 0.36 > ry2^2 [1] 0.16 > r12^2 [1] 0.09 >
> lm.m.pa <- lm(Memory~Practice+Anxiety, data=CorrDataT)
> summary(lm.m.pa)
Call:
lm(formula = Memory ~ Practice + Anxiety, data = CorrDataT)
Residuals:
Min 1Q Median 3Q Max
-1.99998 -0.54360 0.04838 0.43878 2.74186
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.30769 0.96783 2.384 0.01905 *
Practice 0.52747 0.08153 6.469 4.01e-09 ***
Anxiety 0.24176 0.08153 2.965 0.00381 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.7739 on 97 degrees of freedom
Multiple R-squared: 0.4132, Adjusted R-squared: 0.4011
F-statistic: 34.15 on 2 and 97 DF, p-value: 5.919e-12
a+b+c+e = variance of y = total variance = 100% = 1 이라고 보면
r2 = a + b + c / a + b + c + e = a + b + c = 0.4132 (from summary(lm.m.pa))
이 중에서 우리는 이미
a + c = 0.62 = 0.36
b + c = 0.42 = 0.16
따라서 Practice를 제어한 Anxiety의 영향력은
r2 - (a+c) = 0.4132 - 0.36 = 0.0532
반대로, Anxiety를 제어한 Practice의 영향력은
r2 - (a+c) = 0.4132 - 0.16 = 0.2532