연구자는 자신의 연구 문제와 관련된 조사대상의 집단을 규정한다. 이 때 규정되는 집단을 모집단 혹은 population이라고 한다. 연구자가 청소년의 mp3 음악 사용에 관한 개념에 관해서 관심을 가지고 이에 따른 연구문제를 제시했다면, 잠정적으로 이 연구에서 규정하는 모집단은 청소년이라고 하겠다. Conceptualization과 Operationalization과 마찬가지로, 모집단에 대한 규정을 명확히 해 놓을 필요가 있다. 즉, 위의 예에서 청소년이라 하면, 구체적으로 어떤 대상인지를 밝혀야 한다.

연구자는 모집단에 대한 명확한 규정을 하였어도, population이 작은 경우나 혹은 census와 같은 경우를 제외하고는, 그 집단 전체를 조사할 수 없는 경우가 많다. 집단 전체를 모두 조사하는 것을 enumeration이라고 하는데, 이런 경우는 높은 비용이 소요되기 때문이다.

따라서, 연구자는 population에서 일정 대상을 선출하여, 이에 대한 조사를 바탕으로 population의 성격을 추론해 내게 된다. 이렇게 선정되는 population의 일부를 sample이라고 한다.

Parameters and statistics

Landon vs Roosevelt Election

Sampling Frame
이렇게 조사의 대상이 되는 population에서 실제로 조사를 할 대상을 선출하는 작업을 샘플링(sampling)한다고 한다. Sampling을 위해서 연구자가 가장 먼저 확보해야 할 것은 population의 리스트이다. 이것을 sampling frame이라고 한다. 가령, 연구자가 청소년의 샘플을 확보하기 위해서 교육부의 중고등학교 학생의 명부를 이용하였다면, 이 명부가 sampling frame이다. 연구자가 전화번호부를 이용하였다면 전화번호부의 명단이 sampling frame이다. Sampling frame와 population의 다른 점은 말 그대로이다. 즉, 중고등학교 학생과 학생명단의 차이점이다.

Sampling에는 두 가지의 방법이 있는데, 첫 째는 non-probability sampling (NPS)이고 둘 째는 probability sampling(PS)이다. 오늘 날 행해지는 큰 규모의 리서치 폴(pole)이나, 서베이는 대개 PS를 기반으로 하는데, 그 주된 이유는 PS를 이용해서 얻어지는 sample은 대표성(representativeness)을 띄기 때문이다. 대통령선거에 관한 여론조사(research pole)가 좋은 예이다. 대표성을 띈다는 말은 곧 샘플조사결과를 일반화(generalization)할 수 있다는 의미이다.

NPS는 선출되는 sample이 대표성(representativeness)을 띄지 않는다. 대표성을 띄는 sample을 얻기가 현실적으로 불가능한 경우가 많은데 이럴 경우는 NPS방법을 쓴다. NPS에는 여러 가지 종류가 있다.

1. 자의적 샘플링 추출방법 reliance on available subjects:편의에 따라서 샘플을 뽑는 작업을 말한다. 흔한 예로, 백화점 앞에서 하는 설문조사이다. 이렇게 해서 얻은 자료는 PS에 의해서 얻은 샘플이 아니므로 일반화하기가 어려운 단점이 있다. 주의해야 할 점은 “명동 시내 거리에서 무작위로 사람을 골라서 설문조사를 하였다”라는 문구의 “무작위” 단어는 “우연”이라는 의미가 있을 뿐, 수학적 혹은 통계학적인 의미에서의 “무작위(random)“이라는 의미는 전혀 내포되어 있지 않다.
2. 목적, 판단 샘플링 purposive or judgmental sampling: 목적, 판단 샘플링은 연구자가 판단하여 자의적으로 샘플을 구성하는 경우를 말한다. 아주 작은 집단을 연구할 때, 구태여 랜덤 샘플링의 (NPS와 같은 뜻으로 쓰임) 방법을 쓸 필요가 없다고 판단되면, 이런 방법을 쓴다. HIV균을 가진 사람들의 사회적인 관계망을 연구하고 싶은 학자가 HIV보균자의 명단을 확보한다는 것은 쉬운 일이 전혀 아니다. 학교 주변 커뮤니티의 소년소녀 가장을 연구하고자 한다면, 굳이 샘플링의 방법을 쓸 필요가 없을 지도 모른다.
3. 눈굴리기 샘플링 (snowballing): 네트워크 샘플링 (Network Sampling)의 다른 이름이며, 연구대상자로 해당되어있는 사람들을 통해 다른 연구대상자를 구하는 방식이다. Building your sample by using your sample이라고 간단하게 설명할 수 있다. 이 경우 Non probability sampling의 취약점인 표본(sample)을 확보할 수 있다는 점에서 많은 연구자들이 선호한다.
4. 구획(쿼터) 샘플링 (Quota sampling): 연구하고자 하는 모집단의 성격을 알아서, 모집단을 일정한 방법으로 구획하여, 샘플을 추출하는 방법을 말한다.

• Representativeness (대표성)
  • ECoBS (Equal Chance of Being Selected)
• Sampling bias (샘플링 바이어스)
  • concscious
  • unconscious

1. simple_random_sampling
   1. with replacement
   2. without replacement
2. Systematic random sampling:
   • $ \displaystyle k = \frac {N}{n} $ where n = sample size, N = population size
3. Stratified sampling: See a video
4. Cluster sampling
   • 지도에서 구역을 블럭화(클러스터화) 하고, 이를 랜덤하게 고른 후, 여기의 개인을 서베이 하는 경우 이를 Cluster sampling 이라고 할 수 있다.
5. Multistage cluster sampling:
6. Stratified in multistage cluster sampling:

• Using spreadsheet (such as Excel, Lotus123 program, and so on)
  • samplerecord.xls
  • iqrandomsample.xlsm
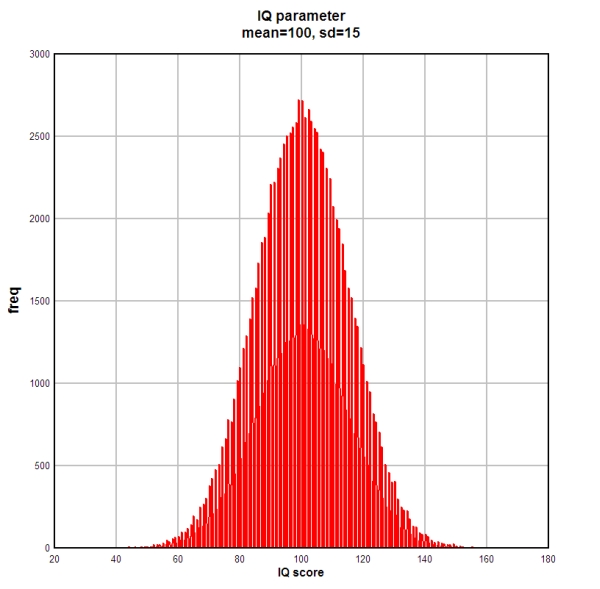
  • 위의 파일(IQRandomSample.xlsm)의 내용은 10만명의 IQ점수를 모아 놓은 population record라고 가정하자.
• 이 때의 Mean, Mode, Median:
  • Mean: 100.02858 = 100
  • Mode: 99
  • Median: 100
  • histogram:

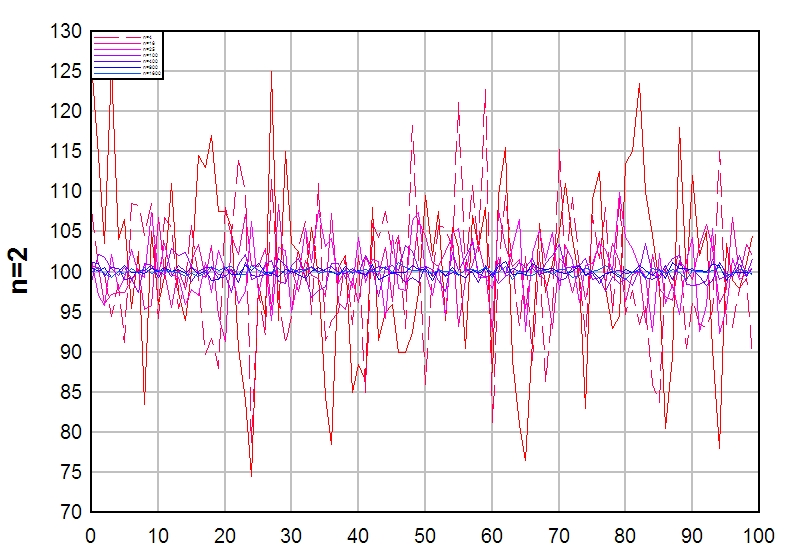
caption=“n=2 4 16 25 100 400 900 1600 일때의 샘플평균들의 분포 (distribution of sampling means)”

rm(list=ls())

var_ <- new.env()
n<-20        ## Sample n individuals at a time
p_mean<-0    ## Population mean
p_sd<-1      ## Population standard deviation
N<-500       ## Number of times the experiment (sampling) is replicated

pdf('SE.pdf')

for(i in 1:N)     ## do the experiment N times
{
smp<-rnorm(n,p_mean,p_sd)    ## sample n data points from the population

var_$x_bar<-c(var_$x_bar,mean(smp))     ## keep track of the mean (x_bar) from each sample

hist(var_$x_bar,probability=TRUE,col="red",xlim=c(-4,4),xlab="x / x_bar",main="",ylim=c(0,2.2))  
# Plot a histogram of x_bar values

points(mean(smp),0,pch=19,cex=1.5,col='black')
curve(dnorm(x,p_mean,p_sd/sqrt(n)),lwd=3,add=TRUE)

text(2.5,1.75,labels=paste('sd/sqrt(n) = ',round(p_sd/sqrt(n),2),sep=''))
text(2.5,1.5,labels=paste('standard deviation of\nsample means = ',round(sd(var_$x_bar),2),sep='') )

curve(dnorm(x,p_mean,p_sd),main="",ylab="",xlim=c(-4,4),xlab="X",col="blue",lwd=3,add=TRUE) 
## Plot the sample

text(2.5,0.5,labels=paste('# of means drawn = ',i,sep=''))
text(2.5,0.35,labels=paste('Sample size (n) = ',n,sep=''))
points(smp,rep(0,n),pch=19,cex=1.5,col='purple')
abline(v= mean(smp),col='purple',lwd=4)

legend("topleft",legend=c('Sample points','Population Distribution','Sample mean','Theoretical SE','Empirical SE'),
lty=c(0,1,1,1,1,1,1),lwd=c(0,3,3,3,3,3,3),pch=c(16,NA,NA,NA,NA,NA,NA),col=c('purple','blue','purple','black','red'))

print(paste(i," of ",N))
}
dev.off()

se.pdf

• Variation See, Variance: 225.0584138 (15^2)
• Standard Deviation Standard Deviation: 15.001947
• Sampling distribution, see, Sampling Distribution
  • Estimated Value of Standard Deviation: Why do we use n-1 instead of n in sample standard deviation?
• Standard Error Standard Error
• Central Tendency