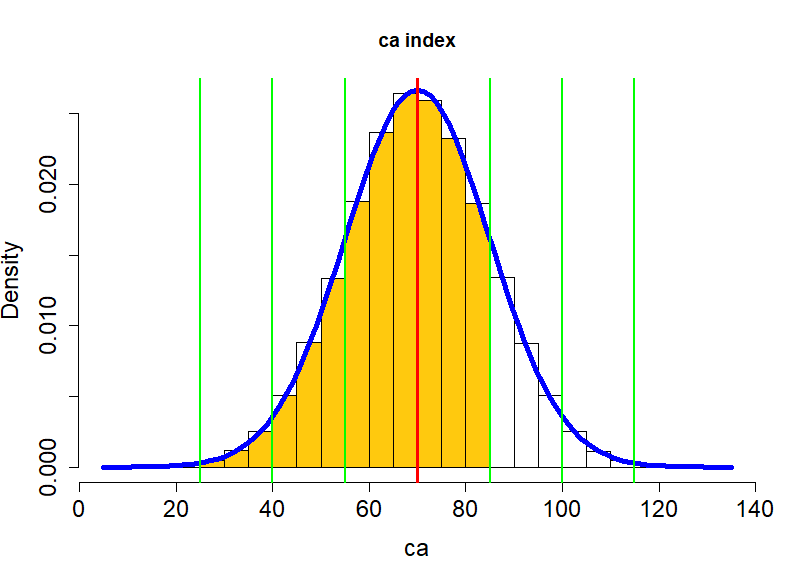
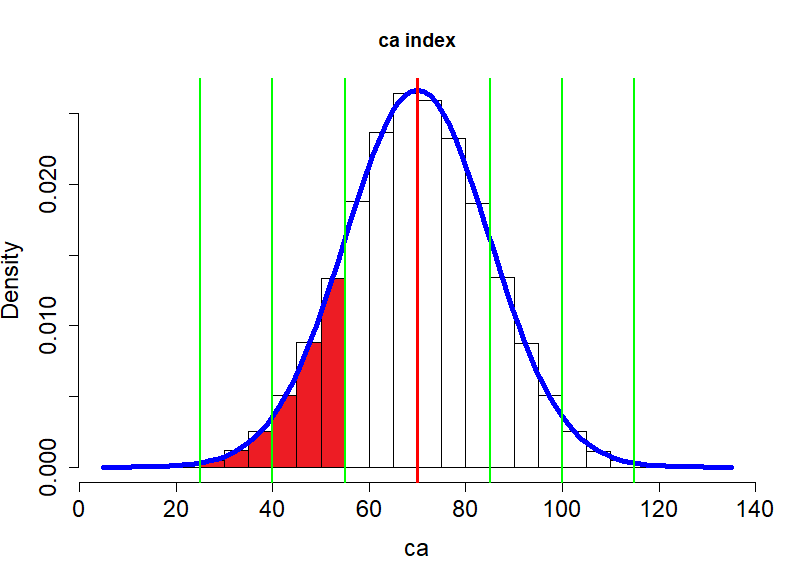
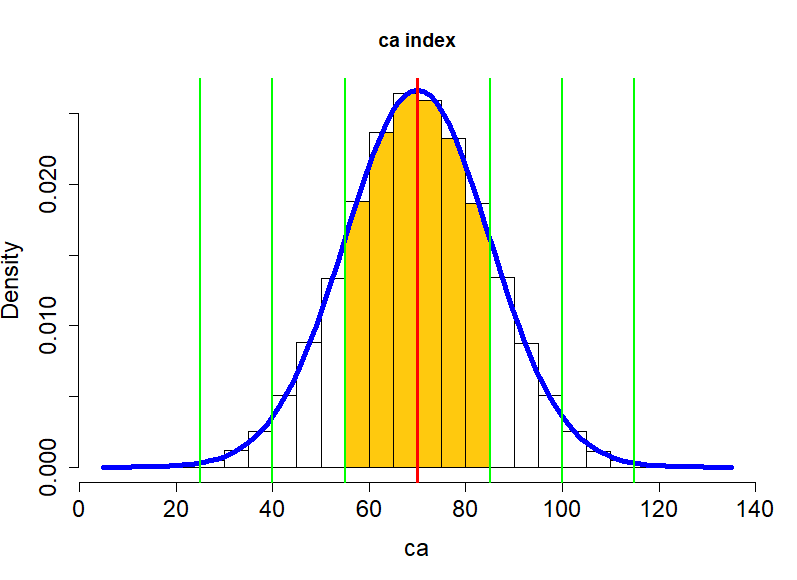
z_score []

평균이 0, 표준편차가 1인 정상분포에서의 개인점수를 말한다.

$\begin{equation} \displaystyle z = \frac {X - \mu} {\sigma}} \end{equation}$

in R, pnorm(zscore) or pnorm(sd)

pnorm(1) - pnorm(-1)
pnorm(2) - pnorm(-2)
pnorm(3) - pnorm(-3)

> pnorm(1) - pnorm(-1)
[1] 0.6826895
> pnorm(2) - pnorm(-2)
[1] 0.9544997
> pnorm(3) - pnorm(-3)
[1] 0.9973002

in R, qnorm(percentage)

qnorm(.025)
qnorm(.975)

qnorm(0.025) 
qnorm(0.975) 

qnorm(0.01)
qnorm(0.99)

qnorm(0.001)
qnorm(0.999)