Table of Contents
Correlation and Regression: What's My Line?
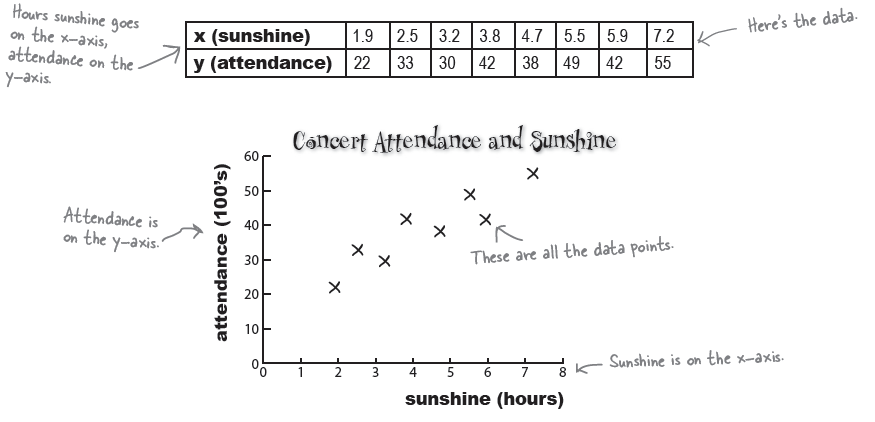
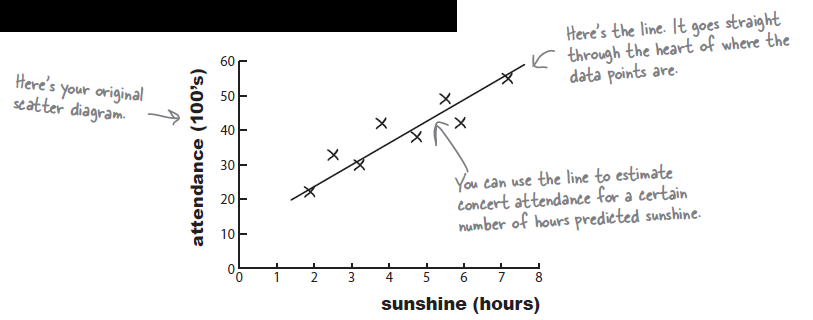
> s <- c(1.9,2.5,3.2,3.8,4.7,5.5, 5.9, 7.2)
> c <- c(22,33,30,42,38,49,42,55)
> plot(s,c)
> df <- data.frame(s,c)
> df
s c
1 1.9 22
2 2.5 33
3 3.2 30
4 3.8 42
5 4.7 38
6 5.5 49
7 5.9 42
8 7.2 55
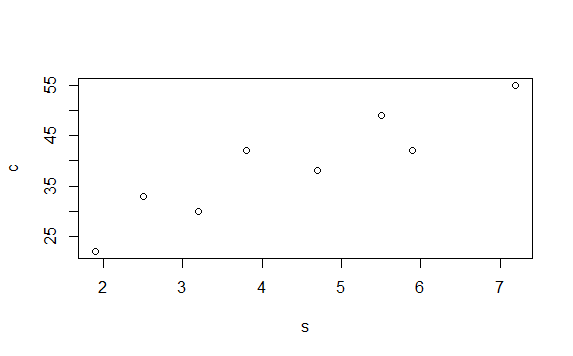
> plot(df)
Predict values with a line of best fit
\begin{align} b = & \frac{\Sigma{(x-\overline{x})(y-\overline{y})}}{\Sigma{(x-\overline{x})^2}} \nonumber \\ = & \frac{SP}{SS_{x}} \\ a = & \overline{y} - b \; \overline{x} \;\;\; \because \; \overline{y} = a + b \; \overline{x} \end{align}
> # lm = linear modeling (lm function)
> # = regression
> # = correlation
> mod <- lm(c~s, data=df)
> summary(mod)
Call:
lm(formula = c ~ s, data = df)
Residuals:
Min 1Q Median 3Q Max
-5.2131 -3.0740 -0.9777 3.9237 5.9933
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.7283 4.4372 3.545 0.01215 *
s 5.3364 0.9527 5.601 0.00138 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.571 on 6 degrees of freedom
Multiple R-squared: 0.8395, Adjusted R-squared: 0.8127
F-statistic: 31.37 on 1 and 6 DF, p-value: 0.001379
Correlation
Textbook says:
\begin{align} r = & b * \frac {sd(x)}{sd(y)} \\ = & b * \sqrt{\frac {SS_X} {SS_Y}} \;\;\; \because \left(b = \frac {SP}{SS_X} \right) \nonumber \\ = & \frac {SP}{SS_X} * \frac {\sqrt{SS_X}} {\sqrt{SS_Y}} \nonumber \\ = & \frac {SP}{\sqrt{SS_X * SS_Y}} \nonumber \\ = & \frac {COV}{SD(X) SD(Y)} \end{align}
Regression page says:
\begin{eqnarray}
R^2 & = & \frac{\text{SS}_{reg}}{\text{SS}_{total}} \\
& = & \frac{ \text{SS}_{total} - \text{SS}_{res}} {\text{SS}_{total}} \nonumber \\
& = & 1 - \frac{\text{SS}_{res}} {\text{SS}_{total}} \\
\end{eqnarray}
\begin{eqnarray*} & \text{Note that (1), (2) are the same.} \nonumber \\ & \text{Therefore,} \nonumber \\ & r = \sqrt{R^2} \\ \end{eqnarray*}
We, from correlation wiki page, also addressed that r (correlation coefficient value) can be obtained through
\begin{eqnarray*}
r & = & \frac {Cov(x,y)} {sd(x)*sd(y)} \\
\end{eqnarray*}
see pearson_s_r
아래는 위의 세 가지 방법으로 R에서 r 값을 구해본 것이다.
# check the coefficient from the lm analysis b <- summary(mod)$coefficients[2,1] b df sd.x <- sd(df$s) sd.y <- sd(df$c) # 첫 번째 r.value1 <- b * (sd.x/sd.y) r.value1 # 두 번째 # rsquared r.value2 <- sqrt(summary(mod)$r.squared) r.value2 # or cov.sc <- cov(df$s, df$c) r.value3 <- cov.sc/(sd.x*sd.y) r.value3
아래는 위의 아웃풋
> # check the coefficient from the lm analysis
> b <- summary(mod)$coefficients[2,1]
> b
[1] 5.336411
> df
s c
1 1.9 22
2 2.5 33
3 3.2 30
4 3.8 42
5 4.7 38
6 5.5 49
7 5.9 42
8 7.2 55
> sd.x <- sd(df$s)
> sd.y <- sd(df$c)
>
> # 첫 번째
> r.value1 <- b * (sd.x/sd.y)
> r.value1
[1] 0.9162191
>
> # 두 번째
> # rsquared
> r.value2 <- sqrt(summary(mod)$r.squared)
> r.value2
[1] 0.9162191
>
> # or
> cov.sc <- cov(df$s, df$c)
> r.value3 <- cov.sc/(sd.x*sd.y)
>
> r.value3
[1] 0.9162191
>
exercise
# correlation 에 대한 이해를 돕기 위한 연습 # stat first 책에서 radiation exposure 양과 # (독립변인) weight 간의 관계 (종속변인) # # 두 변인 (독립변인과 종속변인) 모두 # 숫자로 측정된 변인 re <- c(4, 4.5, 5, 5.5, 6, 6.5, 7) we <- c(12, 10, 8, 9.5, 8, 9, 6) # 손으로 variance, standard deviation 구하기 # 우선 각각의 평균 mean.re <- mean(re) mean.we <- mean(we) mean.re mean.we # sum of square x (ssx) 와 ssy 구하기 ss.re <- sum((re-mean.re)^2) ss.we <- sum((we-mean.we)^2) ss.re ss.we # df 값은 df <- length(we)-1 df # variance와 sd var.re.1 <- ss.re/df var.we.1 <- ss.we/df sd.re.1 <- sqrt(var.re.1) sd.we.1 <- sqrt(var.we.1) # R의 펑션을 이용해서 구하기 var.re <- var(re) var.we <- var(we) sd.re <- sd(re) sd.we <- sd(we) var.re.1 var.we.1 var.re var.we sd.re.1 sd.we.1 sd.re sd.we # sum of product sp <- sum((re-mean.re)*(we-mean.we)) cov.rewe.1 <- sp/df cov.rewe <- cov(re,we) sp cov.rewe.1 cov.rewe # 교재에 기술된 # r, b, r square # r = cov(x,y)/(sd(x)*sd(y)) # = sp / sqrt(ss(x)*ss(y)) r.val <- sp / (sqrt(ss.re*ss.we)) r.val2 <- cor(re,we) r.val r.val2 # 기울기 b = sp / ss(x) b <- sp / ss.re b a <- mean.we - (b * mean.re) a # r 제곱값 (r^2) r.sq <- r.val^2 r.sq # 위의 모든 정보가 lm function의 결과에 m1 <- lm(we~re) summary(m1) ## summary(m1)에서 se가 나타나는 부분 설명 # se of regression = sqrt of mse # p = # of parameters (IVs) # p <- 1 n <- length(we) n df.res <- n-p-1 # or m1$df.residual # residual 값들을 제곱해서 모두 더한 후 # n으로 (df.residual값으로) 나누준 것 # = 분산을 구하는 형식이다. 즉 아래는 # regression line으로 예측하고 남은 # 나머지 오차들에 (residuals) 대한 분산값 # 이것을 mean square error라고 부른다 # variance를 mean square라고 부르는 사람들이 # 있다. # ss of square residuals = ssres ssres <- sum(m1$residuals^2) # ssres = sum of square error 값으로 부르기도 # 한다. sse <- ssres mse <- sse/df.res mse # 그리고 그 값에 sqrt값을 씌워 sd값을 # stanard deviation 구한다. 이것을 # root mean square error라고 부른다. rmse <- sqrt(mse) rmse # summary(m1)에서 Residual standard error: 1.177 # 에 해당하는 값 summary(m1) # b coefficient 에 대한 standard error 값은 # sqrt( (1/(n-2)) * (sse/ssx)) se.b <- sqrt( (1/(n-2)) * (sse/ss.re) ) se.b # 아래 아웃풋에서 Std. Error 참조 summary(m1) c <- qt(.975, 5) se.b2 <- c*se.b b - se.b2 b + se.b2 confint(m1)
> # correlation 에 대한 이해를 돕기 위한 연습
> # stat first 책에서 radiation exposure 양과
> # (독립변인) weight 간의 관계 (종속변인)
> #
> # 두 변인 (독립변인과 종속변인) 모두
> # 숫자로 측정된 변인
> re <- c(4, 4.5, 5, 5.5, 6, 6.5, 7)
> we <- c(12, 10, 8, 9.5, 8, 9, 6)
>
> # 손으로 variance, standard deviation 구하기
> # 우선 각각의 평균
> mean.re <- mean(re)
> mean.we <- mean(we)
> mean.re
[1] 5.5
> mean.we
[1] 8.928571
>
> # sum of square x (ssx) 와 ssy 구하기
> ss.re <- sum((re-mean.re)^2)
> ss.we <- sum((we-mean.we)^2)
> ss.re
[1] 7
> ss.we
[1] 21.21429
>
> # df 값은
> df <- length(we)-1
> df
[1] 6
> # variance와 sd
> var.re.1 <- ss.re/df
> var.we.1 <- ss.we/df
> sd.re.1 <- sqrt(var.re.1)
> sd.we.1 <- sqrt(var.we.1)
> # R의 펑션을 이용해서 구하기
> var.re <- var(re)
> var.we <- var(we)
> sd.re <- sd(re)
> sd.we <- sd(we)
>
> var.re.1
[1] 1.166667
> var.we.1
[1] 3.535714
> var.re
[1] 1.166667
> var.we
[1] 3.535714
> sd.re.1
[1] 1.080123
> sd.we.1
[1] 1.88035
> sd.re
[1] 1.080123
> sd.we
[1] 1.88035
>
>
> # sum of product
> sp <- sum((re-mean.re)*(we-mean.we))
> cov.rewe.1 <- sp/df
> cov.rewe <- cov(re,we)
> sp
[1] -10
> cov.rewe.1
[1] -1.666667
> cov.rewe
[1] -1.666667
>
>
> # 교재에 기술된
> # r, b, r square
> # r = cov(x,y)/(sd(x)*sd(y))
> # = sp / sqrt(ss(x)*ss(y))
> r.val <- sp / (sqrt(ss.re*ss.we))
> r.val2 <- cor(re,we)
> r.val
[1] -0.8206099
> r.val2
[1] -0.8206099
>
> # 기울기 b = sp / ss(x)
> b <- sp / ss.re
> b
[1] -1.428571
> a <- mean.we - (b * mean.re)
> a
[1] 16.78571
> # r 제곱값 (r^2)
> r.sq <- r.val^2
> r.sq
[1] 0.6734007
>
> # 위의 모든 정보가 lm function의 결과에
> m1 <- lm(we~re)
> summary(m1)
Call:
lm(formula = we ~ re)
Residuals:
1 2 3 4 5 6 7
0.9286 -0.3571 -1.6429 0.5714 -0.2143 1.5000 -0.7857
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.7857 2.4872 6.749 0.00108 **
re -1.4286 0.4449 -3.211 0.02371 *
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.177 on 5 degrees of freedom
Multiple R-squared: 0.6734, Adjusted R-squared: 0.6081
F-statistic: 10.31 on 1 and 5 DF, p-value: 0.02371
>
> ## summary(m1)에서 se가 나타나는 부분 설명
> # se of regression = sqrt of mse
> # p = # of parameters (IVs)
> #
> p <- 1
> n <- length(we)
> n
[1] 7
> df.res <- n-p-1
> # or
> m1$df.residual
[1] 5
>
> # residual 값들을 제곱해서 모두 더한 후
> # n으로 (df.residual값으로) 나누준 것
> # = 분산을 구하는 형식이다. 즉 아래는
> # regression line으로 예측하고 남은
> # 나머지 오차들에 (residuals) 대한 분산값
> # 이것을 mean square error라고 부른다
> # variance를 mean square라고 부르는 사람들이
> # 있다.
> # ss of square residuals = ssres
> ssres <- sum(m1$residuals^2)
> # ssres = sum of square error 값으로 부르기도
> # 한다.
> sse <- ssres
> mse <- sse/df.res
> mse
[1] 1.385714
>
> # 그리고 그 값에 sqrt값을 씌워 sd값을
> # stanard deviation 구한다. 이것을
> # root mean square error라고 부른다.
> rmse <- sqrt(mse)
> rmse
[1] 1.177164
>
> # summary(m1)에서 Residual standard error: 1.177
> # 에 해당하는 값
> summary(m1)
Call:
lm(formula = we ~ re)
Residuals:
1 2 3 4 5 6 7
0.9286 -0.3571 -1.6429 0.5714 -0.2143 1.5000 -0.7857
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.7857 2.4872 6.749 0.00108 **
re -1.4286 0.4449 -3.211 0.02371 *
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.177 on 5 degrees of freedom
Multiple R-squared: 0.6734, Adjusted R-squared: 0.6081
F-statistic: 10.31 on 1 and 5 DF, p-value: 0.02371
>
> # b coefficient 에 대한 standard error 값은
> # sqrt( (1/(n-2)) * (sse/ssx))
> se.b <- sqrt( (1/(n-2)) * (sse/ss.re) )
> se.b
[1] 0.444926
> # 아래 아웃풋에서 Std. Error 참조
> summary(m1)
Call:
lm(formula = we ~ re)
Residuals:
1 2 3 4 5 6 7
0.9286 -0.3571 -1.6429 0.5714 -0.2143 1.5000 -0.7857
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.7857 2.4872 6.749 0.00108 **
re -1.4286 0.4449 -3.211 0.02371 *
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.177 on 5 degrees of freedom
Multiple R-squared: 0.6734, Adjusted R-squared: 0.6081
F-statistic: 10.31 on 1 and 5 DF, p-value: 0.02371
>
> c <- qt(.975, 5)
> se.b2 <- c*se.b
> b - se.b2
[1] -2.57229
> b + se.b2
[1] -0.2848526
> confint(m1)
2.5 % 97.5 %
(Intercept) 10.39213 23.1792968
re -2.57229 -0.2848526
>
exercise 2: 직접해보기
아래에서처럼 데이터를 R에서 다운로드 받아서 정리한 후에 위에서처럼 sp, ss.x, ss.y, b, a, r, r squared, 등등을 구해 보시오.
########################
dat <- read.csv("http://commres.net/wiki/_media/regression01-bankaccount.csv")
# data
# bankaccount = 통장갯수
# income = 수입
# famnum = 부양가족수
# IV = 수입 = income
# DV = 통장갯수 = bankaccount
#
# 컬럼 이름 바꾸기 (간단하게)
colnames(dat) <- c("y", "x", "x2")
dat
attach(dat)
dat
# ss.y
# ss.x
# df.y
# df.x
# sp.xy
# sd.x
# sd.y
# b coefficient
# b
# a intercept
# a
# pred <- a + b*x
# resid <- y - pred
# ss.pred
# ss.resid
# ss.y
# r
# r.sq