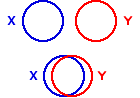Table of Contents
r
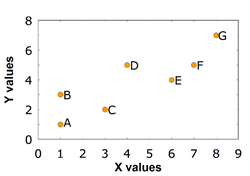
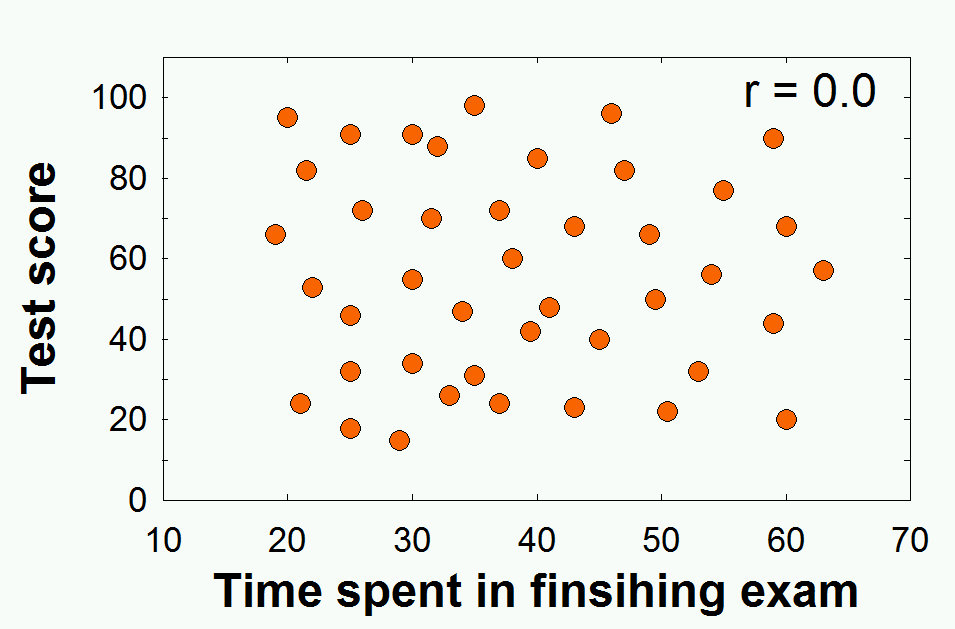
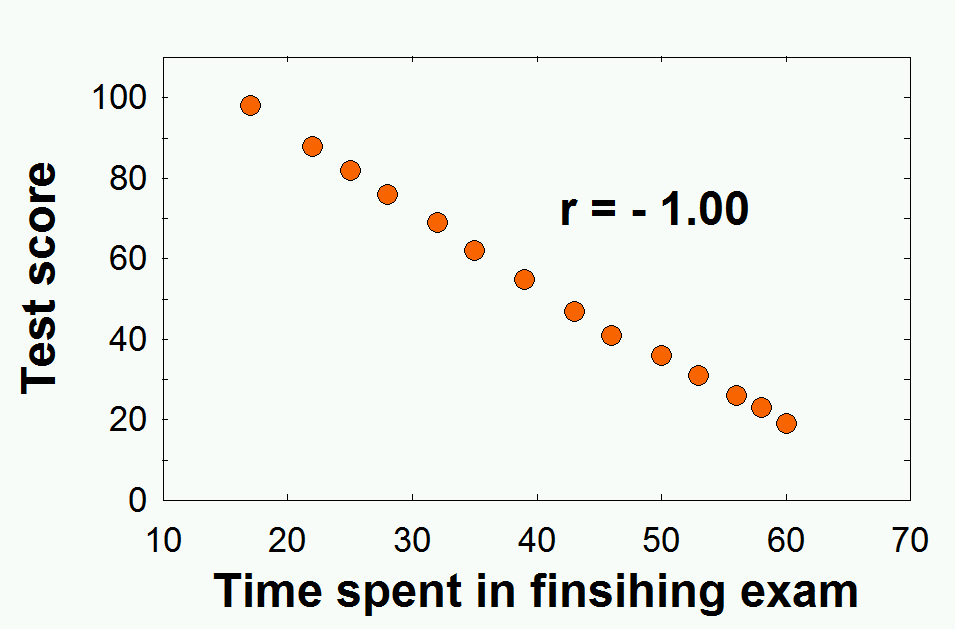
상관관계이란 (correlation) 두 변인 간의 관계를 측정하고 묘사하기 위한 통계학적 기법을 뜻한다. 상관관계 측정은 실험보다는 현상에 대한 관찰 기록에 많이 사용된다. 가령 11살 아동의 키와 몸무게의 관계에 관심을 갖는다는 것은, 키라는 변인과 몸무게라는 변인1) 간의 관계를 알아보려 하는 것이다. 흔히 두 변인은 X 와 Y 로 사용되며, 아래의 그림처럼, 표와 그래프가 데이터 표현에 이용된다.
상관관계의 특징
상관관계는 아래 세 가지 특징을 갖는다.
관계의 방향성
관계의 방향성에 대해서 알려준다. + 사인의 경우, 선형적인 관계가 양의 관계임을, - 사인인 경우에는 음의 관계를 나타내준다고 해석한다.
관계의 형태 (form)
관계의 정도 (힘)
r의 힘을 판단하는 가이드 라인
| Coefficient, r | ||
|---|---|---|
| Strength of Association | Positive | Negative |
| Small | 0.1 ~ 0.3 | -0.1 ~ -0.3 |
| Medium | 0.3 ~ 0.5 | -0.3 ~ -0.5 |
| Large | 0.5 ~ 1.0 | -0.5 ~ -1.0 |
그러나, df를 참조하여 correlation coefficient table을 참조하여 판단할 것
상관관계가 사용되기 위한 조건
- 두 변인 모두의 측정수준이 I 혹은 R 이어야 한다 (NOIR 중. 측정수준 참조).
- 두 변인의 분포가 정상분포에 가까와야 한다.
- 두 변인의 관계가 선형적이어야 한다.
- 아웃라이어가 제어되어야 한다.
- 데이터의 분포가 homoscedasticity를 결과해야 한다
상관관계가 사용될 때
- prediction 예측
- 대학생활 만족도와 졸업 10년 후 행복지수에 대한 데이터를 지속적으로 모아서 관측, 분석을 하게 되면;
- 만족도만을 아는 상태에서 . . .
- Validity 측정
- Validity test: Comparing r to other verified methods in order to confirm (check) my method is valid.
- 내가 고안한 IQ 테스트 방법은 비록 원 IQ 테스트 방법과 다르지만, 결과 값은 서로 상관관계가 높다.
- Theory backup
- Reliablity 측정
- Half-and-half reliability test.
공분산
\begin{eqnarray*}
\text{cov(x, y)} & = & \frac{\Sigma_{i-1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{n-1} \\
& = & \frac{SP}{(n-1)}
\end{eqnarray*}
공분산 값은 x와 y의 단위에 의한 영향을 받는다. 따라서 이 값을 x와 y의 표준편차 값으로 나누어 준것을 피어슨의 상관계수 (Pearson's correlation)라고 한다.
\begin{eqnarray*} \text{corr(x, y)} & = & \frac{\text{cov(x, y)}}{\text{sd(x)} \text{sd(y)}} \\ & = & \frac{\text{cov(x, y)}}{\sqrt{\text{var(x)} \text{var(y)} } } \end{eqnarray*}
아래가 이를 설명한다.
Pearson's r
Pearson's r:: 두 변인 간의 선형적 관계의 크기와 방향성을 측정하는 방법
\begin{eqnarray}
r & = & \frac{\text{degree to which X and Y vary together}}{\text{degree to which X and Y vary separately}} \nonumber \\
& = & \frac{\text{covariablity of X and Y}}{\text{variability of X and Y separately}} \nonumber \\
& = & \frac{Cov[X,Y]}{\sqrt{Var[X]Var[Y]}} \\
& = & \frac{SP_{XY}}{\sqrt{SS_X SS_Y}}
\end{eqnarray}
위에서 (1), (2)는 동일하다. 왜냐하면 . . . . $Cov[X,Y]$ 와 $Var[X]$, $Var[Y]$에 공히 들어가는 분모는 $n-1$ (degrees of freedom)이기 때문이다. 이를 그림으로 나타내 보면 아래와 같다.
이 그림에서 각각의 동그라미는 X 변인과 Y 변인의 variability, 즉 variance를 의미한다고 하면, 위의 그림은 X와 Y가 변하는 정도가 동그라미 정도의 크기를 가지며 (즉 각각의 분산이 동그라미 크기정도라는 뜻이다), 각각의 요소들이 서로 따로따로 논다는 것을 알 수 있다. 즉, Co-vary하지 않다는 것을 알 수 있다. 반면, 아래의 예는 X와 Y의 변하는 정도가 나타나면서 동시에, 각 변인이 서로 동시에 변하는 정도가 어느정도인지 가늠을 할 수 있게 해 준다. Y 입장에서 보면 Y가 변하는 정도 붉은 동그라미 크기 중에서 X와 겹치는 정도를 제외한 정도는 X와 함께 변하는 것이 아닌, Y 고유의 변화정도이다. 이를 residual variance라고 하고, 겹치는 정도는 regression variance라고 이야기 하는데, 이에 대해서는 다음에 설명하도록 한다. 또한 X와 겹치는 변량(X와 Y가 동시에 변화하는 것을 고려한 변량 = $Cov[X, Y]$ )과 Y 전체 변량(분산)의 비율을 $r^2$ 이라고 하는데 이는 r 값을 제곱하여 구한다. 반대로, X와 겹치지 않는 변량과 전체 변량의 비율은 ( $1 - r^2$ )으로 표현한다.
Sum of Products of Deviations
\begin{eqnarray} SP & = & \displaystyle \sum (X-\overline{X})(Y-\overline{Y}) \nonumber \\ & = & \displaystyle \sum XY - \displaystyle \frac{\sum X \small \sum Y}{n} \nonumber \end{eqnarray}
Deviation score = $(X-\overline{X})$ 이라고 할 때, 우리가 관심이 있는 것은 어떤 한 케이스의 X가 변화할 때, 해당 케이스의 y값이 어떻게 (동시에) 변화하는가이므로, 이 상황에 맞는 deviation score는 $(X-\overline{X})(Y-\overline{Y})$ 라고 할 수 있다. 이에 degress of freedom에 해당하는 $n-1$ 로 나누어 준 값을 X,Y에 대한 Covariance라고 하며, $Cov[X,Y]$ 라고 표기한다. 즉,
$$ COV_{xy} = \dfrac{SP}{n-1} $$
참고: SS 또한 SP와 같은 형식을 같는다. 단지 SS는 두 변인을 동시에 살펴보지 않고 한 변인만을 다루므로 같은 값을 두번 곱하여 구할 뿐이다.
\begin{eqnarray*}
SS & = & \Sigma(X-\overline{X})^2 \\
& = & \Sigma(X-\overline{X})(X-\overline{X}) \\
& = & \Sigma X^2 - \frac{(\sum X)^2}{n} \\
& = & \Sigma XX - \frac{\sum X \sum X}{n}
\end{eqnarray*}
e.g. 1,
| Example | |||||
|---|---|---|---|---|---|
| Variable | Variable | Deviation score | Products | ||
| X | Y | $(X-\overline{X})$ | $(Y-\overline{Y})$ | $(X-\overline{X})(Y-\overline{Y})$ | |
| 1 | 3 | -2 | -2 | +4 | |
| 2 | 6 | -1 | +1 | -1 | |
| 4 | 4 | +1 | -1 | -1 | |
| 5 | 7 | +2 | +2 | +4 | |
| sum | 20 | +6 = SP | |||
X 평균 = 3
Y 평균 = 5
이 예는 $ SP = \Sigma (X-\overline{X})(Y-\overline{Y})$ 의 공식을 사용하여 구한 예이다. 반면에, $ SP = \Sigma XY - \frac{\sum X \sum Y}{n}$ 의 공식을 사용하면,
\begin{eqnarray}
SP & = & \sum XY - \frac{\sum X \sum Y}{n} \nonumber \\
& = & 66 - \frac{(12)\;(20)}{4} \nonumber \\
& = & 66 - 60 \nonumber \\
& = & 6 \nonumber
\end{eqnarray}
으로 똑같은 결과를 갖는다. 위는 Sum of Products (SP) 의 값을 구한 것이고 $SS_X$ 와 $SS_Y$ 값을 구해 보면:
| Example | ||||
|---|---|---|---|---|
| X | Y | XY | X2 | Y2 |
| 1 | 3 | 3 | 1 | 9 |
| 2 | 6 | 12 | 4 | 36 |
| 4 | 4 | 16 | 16 | 16 |
| 5 | 7 | 35 | 25 | 49 |
| $\textstyle \sum X = $ 12 | $\textstyle \sum Y =$ 20 | $\textstyle \sum XY = $ 66 | $\textstyle \sum X^2 = $ 46 | $\textstyle \sum Y^2 = $ 110 |
\begin{eqnarray} SS_{\small X} & = & \sum X^2 - \frac{(\sum X)^2}{n} \nonumber \\ & = & 46 - \frac{(12)^2}{4} \nonumber \\ & = & 46 - 36 \nonumber \\ & = & 10 \nonumber \end{eqnarray}
\begin{eqnarray} SS_{\small Y} & = & \sum Y^2 - \frac{(\sum Y)^2}{n} \nonumber \\ & = & 110 - \frac{(20)^2}{4} \nonumber \\ & = & 110 - 100 \nonumber \\ & = & 10 \nonumber \end{eqnarray}
그런데 왜 다음과 같은 공식인지는
\begin{align}
SS_{\small{X}} = \sum X^2 - \frac{(\sum X)^2}{n} \label{ss.simplified} \tag{SS simplified} \\
\end{align}
우선
\begin{align} Var[X] & = \frac {SS_{\small{X}}}{df} \;\;\; \nonumber \\ & \text{Let's assume that } df \nonumber \\ & \text{is n instead of n-1} \nonumber \\ & \text{And we also know that} \nonumber \\ Var[X] & = E[X^2] − (E[X])^2 \;\; \nonumber \\ & = \frac {\Sigma {X^2}}{n} - \left(\frac{\Sigma{X}}{n} \right)^2 \nonumber \\ & = \frac {\Sigma {X^2}}{n} - \frac{(\Sigma{X})^2}{n^2} \nonumber \\ & \therefore \nonumber \\ SS_{\small{X}} & = \Sigma {X^2} - \frac{(\Sigma{X})^2}{n} \;\;\;\;\; \text{That is, } \; \ref{ss.simplified} \nonumber \\ \end{align}
또한
\begin{align}
SP & = & \sum XY - \frac{\sum X \sum Y}{n} \label{sp.simplified} \tag{SP simplified} \\
\end{align}
\begin{align} Cov[X,Y] & = E[(X-\overline{X})(Y-\overline{Y})] \nonumber \\ & = E[XY - X \overline{Y} - \overline{X} Y - \overline{X} \overline{Y}] \nonumber \\ & = E[XY] - E[X] \overline{Y} - \overline{X} E[Y] + \overline{X} \overline{Y} \nonumber \\ & \because \;\;\; E[c] = c \;\;\; \text{and, } \overline{X} = E[X] \nonumber \\ & = E[XY] - E[X]E[Y] - E[X]E[Y] + E[X]E[Y] \nonumber \\ & = E[XY] - E[X]E[Y] \nonumber \\ & = \frac{\Sigma{XY}}{n} - \frac{\Sigma{X}}{n} \frac{\Sigma{Y}}{n} \nonumber \\ & \therefore \nonumber \\ SP & = \Sigma{XY} - \frac{\Sigma{X} \Sigma{Y}}{n} \;\;\;\;\; \text{That is, } \; \ref{sp.simplified} \nonumber \\ \end{align}
이제 r (correlation coefficient) 값은:
\begin{eqnarray} r & = & \frac{SP}{\sqrt{SS_X SS_Y}} \nonumber \\ & = & \textstyle \frac{6}{\sqrt{(10)(10)}} \nonumber \\ & = & \textstyle .6 \nonumber \end{eqnarray}
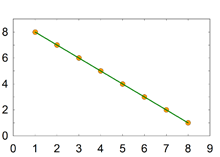
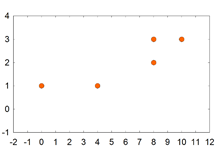
e.g. 2,
테이블의 데이터에 대한 scatterplot을 그려 보면 그림과 같다.
| Example 2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Scores | Deviation score | Deviation score2 | Products | |||||
| X | Y | X2 | Y2 | $(X-\overline{X})$ | $(Y-\overline{Y})$ | $(X-\overline{X})^2$ | $ (Y-\overline{Y})^2 $ | $(X-\overline{X})$ $ * (Y-\overline{Y})$ |
| 0 | 1 | 0 | 1 | -6 | -1 | 36 | 1 | 6 |
| 10 | 3 | 100 | 9 | 4 | 1 | 16 | 1 | 4 |
| 4 | 1 | 16 | 2 | -2 | -1 | 4 | 1 | 2 |
| 8 | 2 | 64 | 4 | 2 | 0 | 4 | 0 | 0 |
| 8 | 3 | 64 | 9 | 2 | 1 | 4 | 1 | 2 |
| t = 30 | 10 | 234 | 24 | SSX = 64 | SSY = 4 | SP = 14 | ||
| $\overline{X}$ = 6 | 2 | |||||||
위에서 구한 SSX, SSY, 그리고 SP 값을 대입해 보면,
\begin{eqnarray} r & = & \frac{SP}{\sqrt{(SS_X) (SS_Y)}} \nonumber \\ & = & \frac{14}{\sqrt{(64) (4)}} \nonumber \\ & = & .875 \nonumber \end{eqnarray}
참고로 아래는 Covariance 대 Variance 비율로 계산한 것
\begin{eqnarray*}
r & = & \frac {Cov(X,Y)} {\sqrt{Var(X) Var(Y)}} \\
r & = & \frac {\frac{SP}{n-1}} {\sqrt{\frac{(SS_X)}{n-1} \frac{(SS_Y)}{n-1}}} \\
\end{eqnarray*}
혹은,
\begin{eqnarray*} SS_{X} & = & \sum X^2 - \frac{(\sum X)^2}{n} \\ & = & 244 - \frac{(30)(30)}{5} \\ & = & 64 \end{eqnarray*}
\begin{eqnarray} SS_{\tiny Y} & = & \sum Y^2 - \frac{(\sum Y)^2}{n} \nonumber \\ & = & 24 - \frac{(10)(10)}{5} \nonumber \\ & = & 4 \nonumber \end{eqnarray}
Pearson's r 의 의미
Relations, not cause-effect
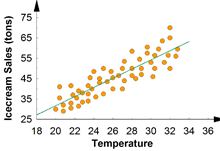
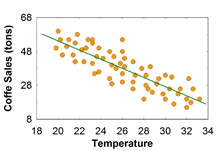
상관관계 계수는 단순히 두 변인 (x, y) 간의 관계가 있다는 것을 알려줄 뿐, 왜 그 관계가 있는지는 설명하지 않는다. 바꿔 말하면, 충분한 r 값을 구했다고 해서 이 값이 두 변인 간의 '원인'과 '결과'의 관계를 말한다고 이야기 하면 안된다. 예를 들면 아이스크림의 판매량과 성범죄가 서로 상관관계에 있다고 해서, 전자가 후자의 원인이라고 단정할 수 있는 근거는 없다. 이는 연구자의 논리적인 판단 혹은 이론적인 판단에 따른다.
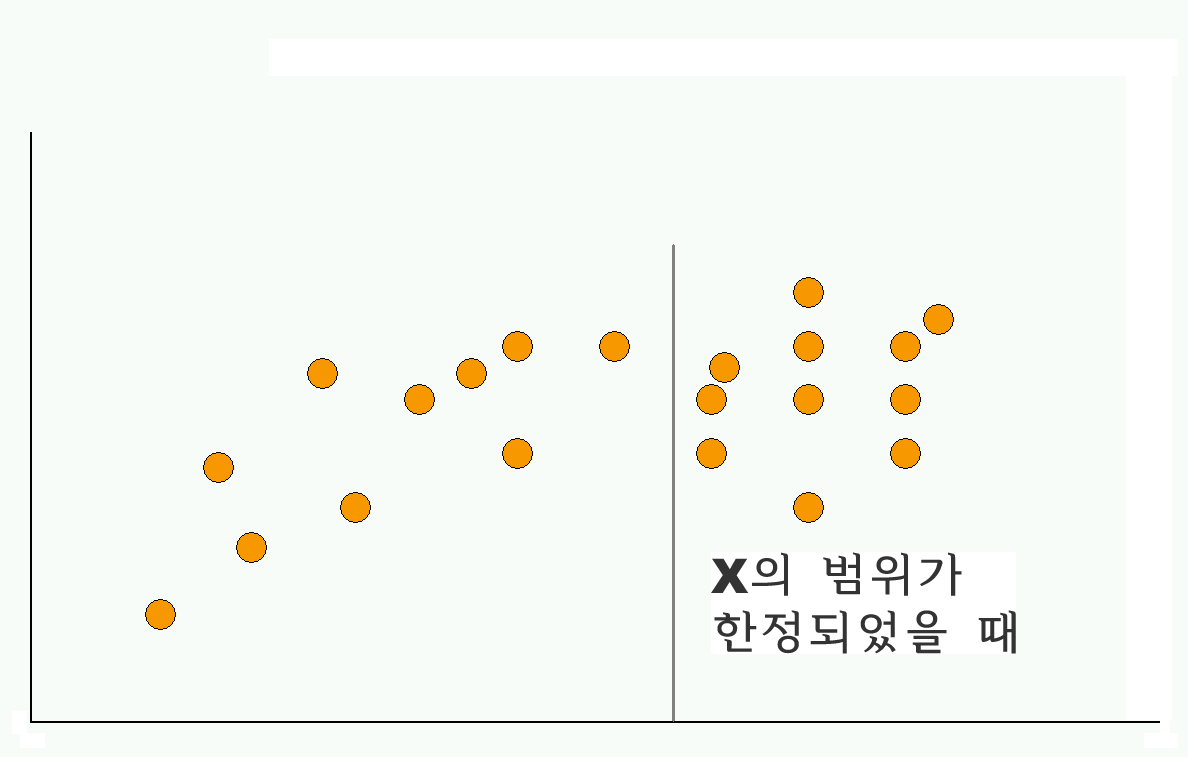
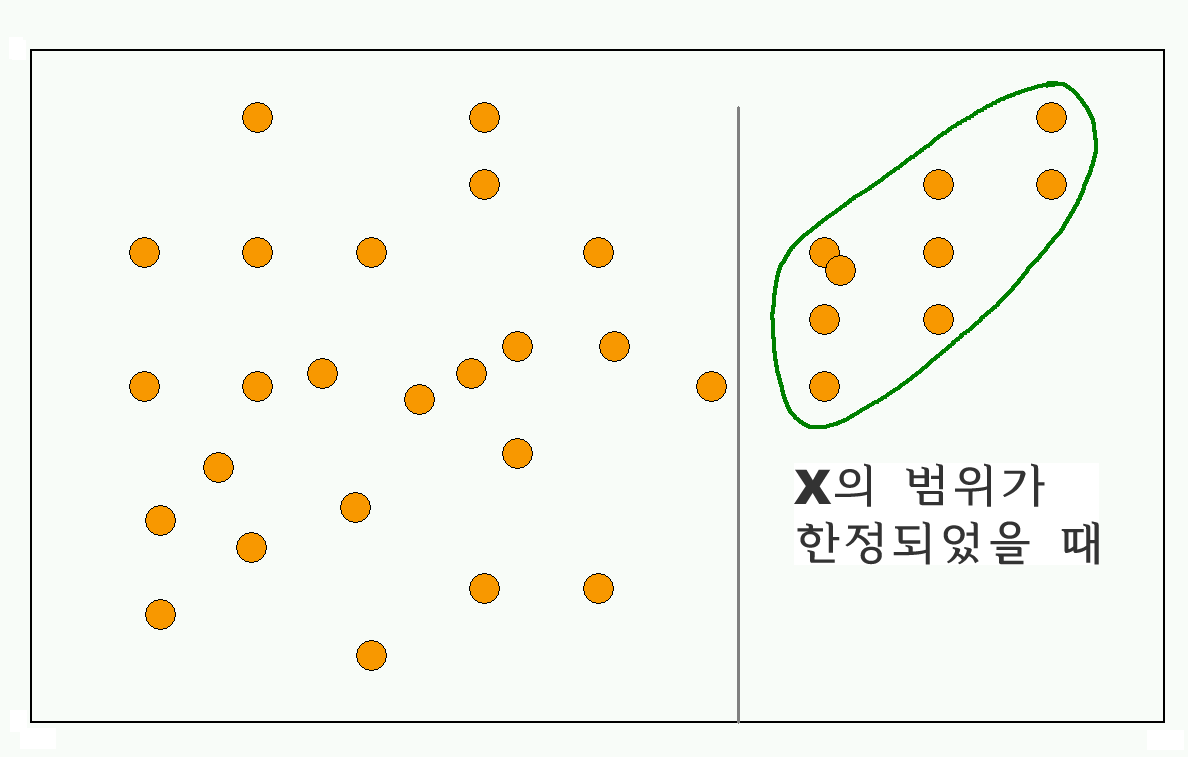
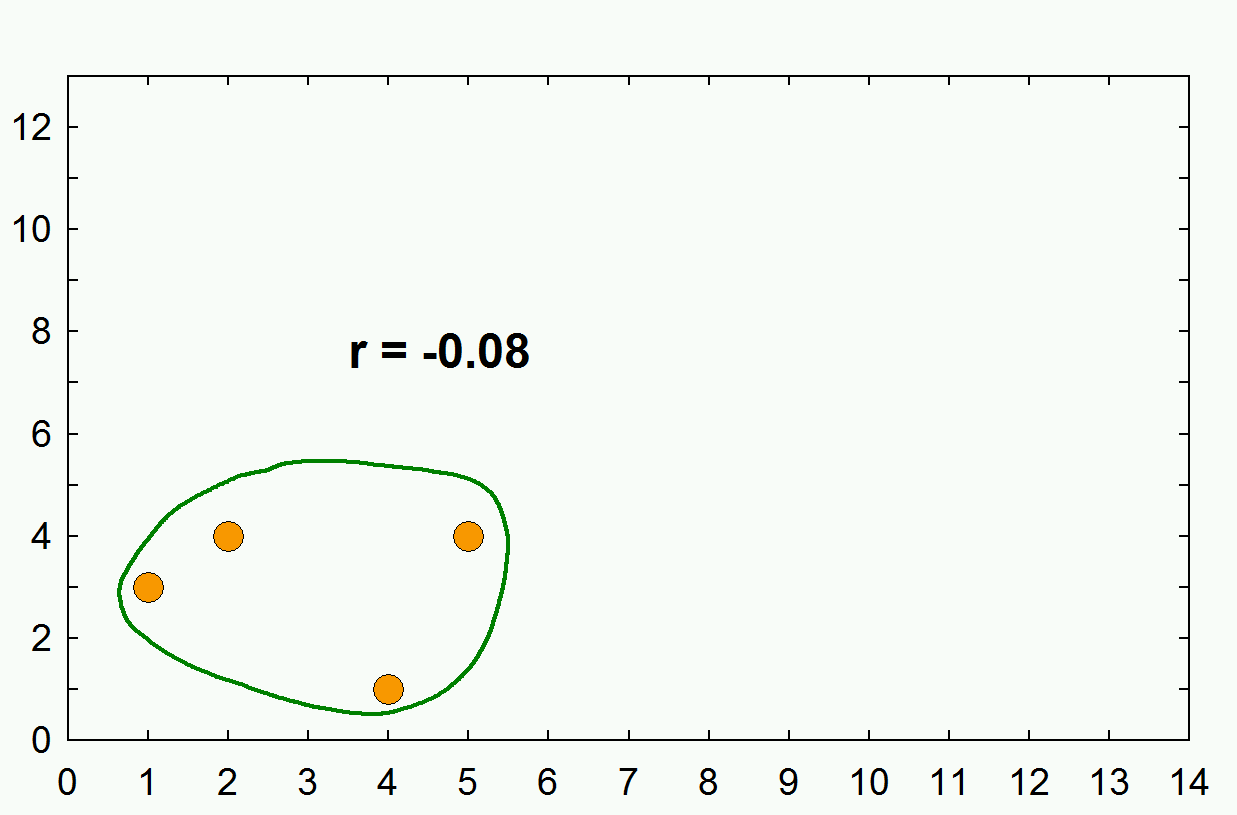
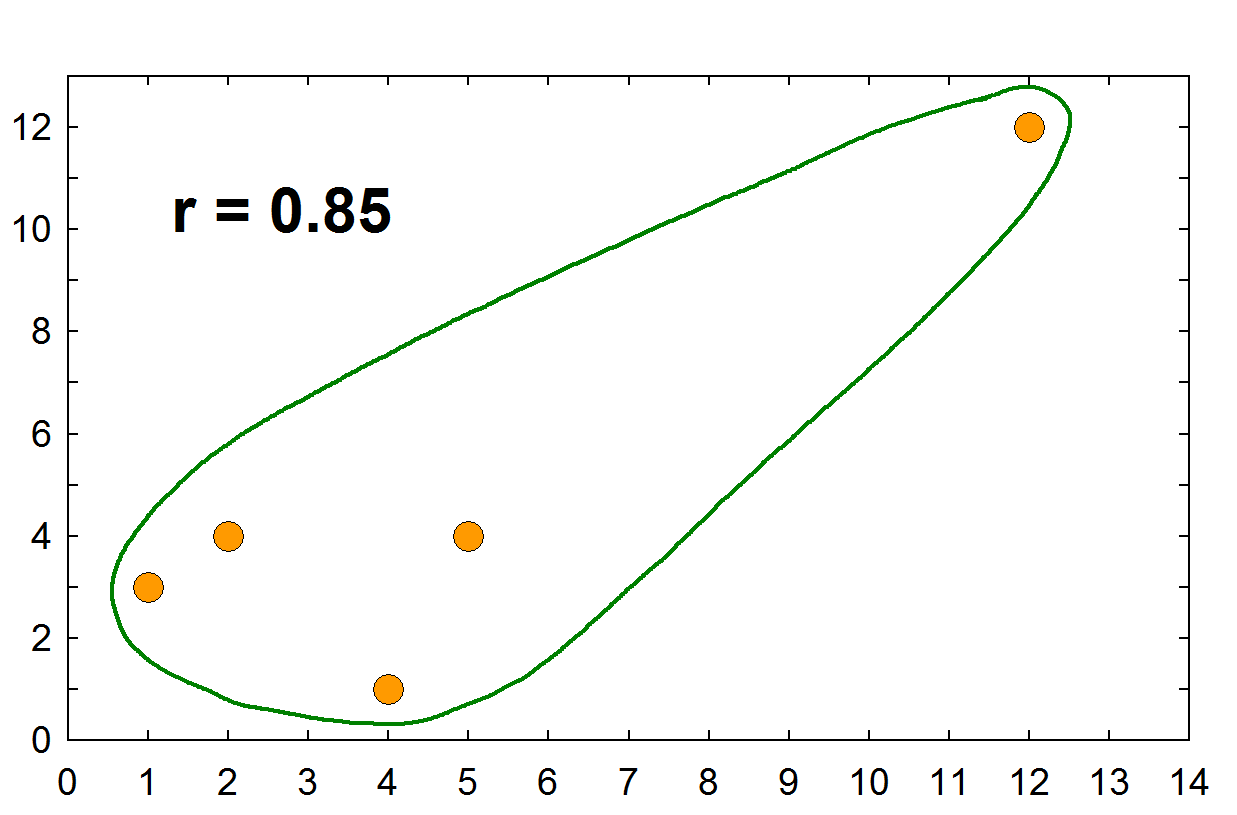
Interpretation with limited range
데이터의 Range에 대한 판단에 신중해야 한다. 왜냐 하면, 데이터의 어느 곳을 자르느냐에 따라서 r 값이 심하게 변하기 때문이다.
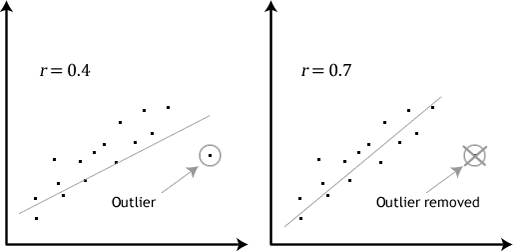
Outliers
위의 설명과 관련하여, 만약에 아주 심한 Outlier가 존재한다면 두 변인 간의 상관관계에 심한 영향을 준다.
Interpretation of r value
r 값으로 얻는 단위는 상관관계의 정도를 정확히 말해 주지 않는다. 예를 들면 r = +.5 은 0 - 1 까지의 반이므로 적당한 량의 상관관계를 보여주고 있다고 생각할 수 있으나, 이는 사실이 아니다. 정확한 양을 이야기 하려면, r 값에 제곱을 해준 값을 이야기 해야 한다. 따라서, r = +.5 인경우 .5^2 값인 .25 즉, 25%가 두 변인 간의 상관관계의 양이다.
Pearson's r을 이용한 가설 검증
기본적으로 두 변인 (보통 한 subject 혹은 participant의 두 변인 기록으로 이루어진 데이터) 간에 상관관계가 있는가에 대한 질문이 연구문제 혹은 가설로 만들어지며, 만약에 이 관계가 없다면, 이라는 질문의 영가설을 통해서 이를 검증한다. 즉,
\begin{eqnarray} & H_0: & \;\; \rho = 0 \;\cdots\; \text{no population correlation} \nonumber \\ & H_1: & \;\; \rho \not= 0 \;\cdots\; \text{real correlation} \nonumber \end{eqnarray}
- correlation의 경우 df는 sample size(n) - number of variables (correlation의 경우 2) 으로 하고
- p value 는 통상적으로 .05으로 참조해서 판단
참조: pearson correlation table 혹은 Pearson's R table PDF파일 혹은 Critical Values for Pearson's Correlation table page 참조
학술논문 보고
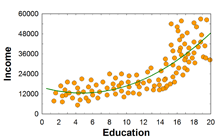
데이터의 상관관계를 살펴본 결과 개인의 교육양과 (년도수) 연수입 (원) 간에는 통계학적으로 유의미한 상관관계가 있다고 판단되었다 (r = +.65, n = 30, p < .01).
연수입, 교육량, 나이, 그리고 지능 간의 관계를 분석하였다 (n=30). 변인들 간의 상관관계를 정리한 결과를 요약한 표1에 나타냈었다. 통계적으로 유의미한 상관관계는 표에 정리되었다.
| TABLE 1. | |||
|---|---|---|---|
| Correlation matrix for income, amount of education, age, and IQ | |||
| Education | Age | IQ | |
| Income | +.65** | +.41** | +.27 |
| Education | +.11 | +.38* | |
| Age | -.02 | ||
| n=30 * p < .05, two tails ** p < .01, two tails |
|||
exercise
- 연구자가 얻은 r = -.41 (n=25) 일때, 이 샘플이 모집단에서 나타나는 두 변인간의 상관관계가 통계적으로 유의미하다고 할 수 있는가?
- n=20 일때, r값은 어떤 값을 가져야 모집단의 두 변인 간의 상관관계가 의미가 있다고 하겠는가?
- 샘플사이즈가 작아질 수 록, 유의미한 상관관계를 갖기 위한 r값은 어떻게 되야 하는가? 왜 그런가?
Spearman Correlation
| Scores | ||
|---|---|---|
| Person | X | Y |
| A | 4 | 9 |
| B | 2 | 2 |
| C | 10 | 10 |
| D | 3 | 8 |
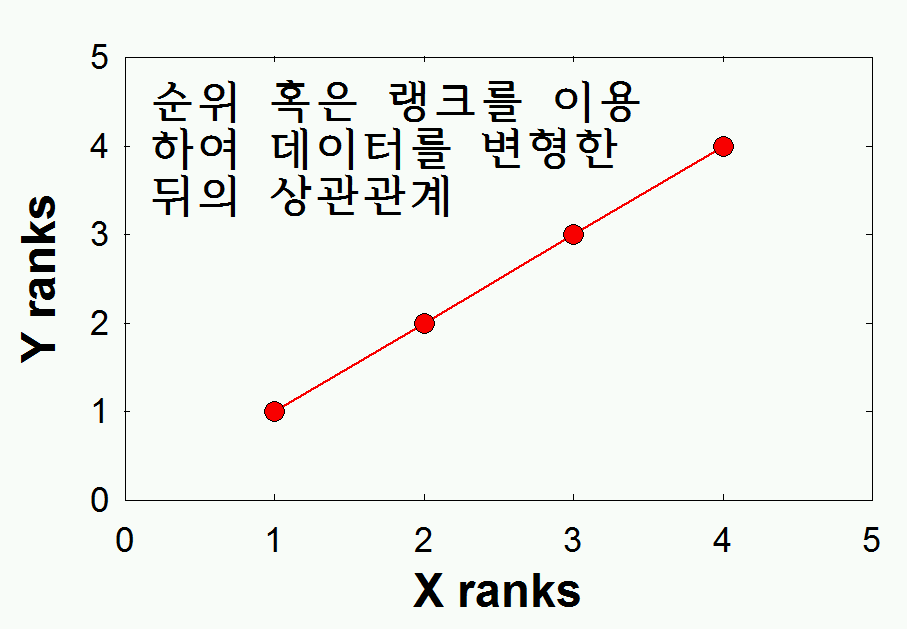
Pearson's r은 두 변인 간의 선형적인 관계를 측정하는 방법이다. 선형적이라 함은 해당되는 변인들의 측정수준이 (LevelOfMeasurement) 숫자 (Interval 혹은 ratio) 형태를 갖는다는 것을 의미한다. 그러나 Ordinal한 측정수준의 데이터 간의 상관관계 또한 구할 수 있다. 이는 Spearman's correlatin이라는 방법을 통해서 구한다. 이를 rank ordered correlation이라고도 한다. 이 데이터의 특징은 상관관계가 존재하되 비선형 관계라는 점이다. 이를 순위를 메겨서 다시 정리하면 아래의 표와 같은 결과를 얻는다.
| Scores | ||
|---|---|---|
| Person | X | Y |
| A | 3 | 3 |
| B | 1 | 1 |
| C | 4 | 4 |
| D | 2 | 2 |
따라서, Spearman rho는
- 순위측정 데이터에 사용 (ordinal measured).
- 상관관계의 지속성에 관심을 둘 때 사용. 즉, 계속 증가하는가, 감소하는 추세인가, 등등에 사용
Spearman's rho 값 구하기
| 순위 | |||||||
|---|---|---|---|---|---|---|---|
| X | Y | X | Y | XY | X2 | Y2 | |
| 3 | 12 | 1 | 5 | 5 | 1 | 25 | |
| 4 | 5 | 2 | 3 | 6 | 4 | 9 | |
| 5 | 6 | 3 | 4 | 12 | 9 | 16 | |
| 10 | 4 | 4 | 2 | 8 | 16 | 4 | |
| 13 | 3 | 5 | 1 | 5 | 25 | 1 | |
| $\Sigma$ | 15 | 15 | 36 | 55 | 55 | ||
\begin{eqnarray} SS_{\tiny X} & = & \sum X^2 - \frac{(\sum X)^2}{n} \nonumber \\ & = & 55 - \frac{15^2}{5} \nonumber \\ & = & 55 - 45 \nonumber \\ & = & 10 \nonumber \end{eqnarray}
$$ SS_{\tiny Y} = 10 $$
\begin{eqnarray} SP_{XY} & = & \sum XY - \frac{(\sum X \sum Y)}{n} \nonumber \\ & = & 36 - \frac{(15)(15)}{5} \nonumber \\ & = & 36-45 \nonumber \\ & = & -9 \nonumber \end{eqnarray}
\begin{eqnarray} r_{\tiny S} \textstyle & = & \frac{SP}{\sqrt{(SS_X)(SS_Y)}} \nonumber \\ & = & \frac{-9}{\sqrt{10(10)}} \nonumber \\ & = & -0.9 \nonumber \end{eqnarray}
Regression
Regression은 이야기할 내용이 많으므로 Regression 참조.
Links
correlation part 1
correlation part 2
correlation part 3
correlation, partial
correlation, rank ordered