$$X \sim Po(\lambda)$$

단위 시간, 단위 공간에 어떤 사건이 몇 번 발생할 것인가를 표현하는 이산 확률분포
모수(population parameter).

• 단위시간 또는 단위공간에서 평균발생횟수
• lambda (λ)로 표시
  • 한 시간 동안 은행에 다녀간 고객의 수
  • 한 시간 동안 사무실에 걸려온 전화의 수
  • 어떤 책의 한 페이지에 존재하는 오타의 수
  • 팝콘 기계가 일주일 동안 고장나는 횟수

조건

• 개별 사건이 주어진 구간에 임의로 그리고 독립적으로 발생
  • 일주일 동안
  • 1마일마다 등 시간이나 공간
• 해당 구간에서 사건이 발생하는 수의 평균값이나 비율을 알고 있음 (lambda($\lambda$))

$$ P(X=r) = e^{- \lambda} \dfrac{\lambda^{r}} {r!},\qquad k = 0, 1, 2, . . ., $$

For curiosity,
\begin{eqnarray*} \sum_{r=0}^{\infty} e^{- \lambda} \dfrac{\lambda^{r}} {r!} & = & e^{- \lambda} \sum_{r=0}^{\infty} \dfrac{\lambda^{r}} {r!} \\ & = & e^{- \lambda} \left(1 + \lambda + \dfrac{\lambda^{2}}{2!} + \dfrac{\lambda^{3}}{3!} + . . . \right) \\ & = & e^{- \lambda}e^{\lambda} \\ & = & 1 \end{eqnarray*}

왜 $e^{\lambda} = \left(1 + \lambda + \dfrac{\lambda^{2}}{2!} + \dfrac{\lambda^{3}}{3!} + . . . \right)$ 인지는 Taylor series 문서를 참조.
이것이 의미하는 것은 r이 0에서 무한대로 갈 때의 확률값의 분포를 말하므로 전체 분포가 1이 됨을 의미한다. 아래 “What does the Poisson distribution look like?” 참조

> e <- exp(1)
> e
[1] 2.718282

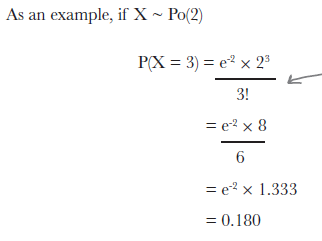
위의 그림은 lambda는 2, 즉 한달에 아주대학교 앞의 건널목 주변 찻길에서 교통사고가 날 횟수가 2회라고 할 때, X=3 이므로 3번 교통사고가 일어날 확률을 (P(X=3)) 묻는 문제이다.
\begin{eqnarray*} P(X = 3) & = & e^{-2} * \frac {2^{3}}{3!} \\ & = & 0.180 \end{eqnarray*}