Why n-1 for 모집단

# variance 
# why we use n-1 when calculating 
# population variance (instead of N)
a <- rnorm2(100000000, 100, 10)
a.mean <- mean(a)
ss <- sum((a-a.mean)^2)
n <- length(a)
df <- n-1
ss/n
ss/df

> # variance 
> # why we use n-1 when calculating 
> # population variance (instead of N)
> a <- rnorm2(100000000, 100, 10)
> a.mean <- mean(a)
> ss <- sum((a-a.mean)^2)
> n <- length(a)
> df <- n-1
> ss/n
[1] 100
> ss/df
[1] 100
> 

# standard deviation 68, 85, 99 rule 
one.sd <- .68
two.sd <- .95
thr.sd <- .99
1-one.sd
(1-one.sd)/2
qnorm(0.16)
qnorm(1-0.16)

1-two.sd
(1-two.sd)/2
qnorm(0.025)
qnorm(0.975)

1-thr.sd
(1-thr.sd)/2
qnorm(0.005)
qnorm(1-0.005)

> # standard deviation 68, 85, 99 rule 
> one.sd <- .68
> two.sd <- .95
> thr.sd <- .99
> 1-one.sd
[1] 0.32
> (1-one.sd)/2
[1] 0.16
> qnorm(0.16)
[1] -0.9944579
> qnorm(1-0.16)
[1] 0.9944579
> 
> 1-two.sd
[1] 0.05
> (1-two.sd)/2
[1] 0.025
> qnorm(0.025)
[1] -1.959964
> qnorm(0.975)
[1] 1.959964
> 
> 1-thr.sd
[1] 0.01
> (1-thr.sd)/2
[1] 0.005
> qnorm(0.005)
[1] -2.575829
> qnorm(1-0.005)
[1] 2.575829
> 
> 

OR the distribution of sample means

# sampling distribution 
n.ajstu <- 100000
mean.ajstu <- 100
sd.ajstu <- 10

set.seed(1024)
ajstu <- rnorm2(n.ajstu, mean=mean.ajstu, sd=sd.ajstu)

mean(ajstu)
sd(ajstu)
var(ajstu)
min.value <- min(ajstu)
max.value <- max(ajstu)
min.value
max.value

iter <- 10000 # # of sampling 

n.4 <- 4
means4 <- rep (NA, iter)
for(i in 1:iter){
  means4[i] = mean(sample(ajstu, n.4))
}

n.25 <- 25
means25 <- rep (NA, iter)
for(i in 1:iter){
  means25[i] = mean(sample(ajstu, n.25))
}

n.100 <- 100
means100 <- rep (NA, iter)
for(i in 1:iter){
  means100[i] = mean(sample(ajstu, n.100))
}

n.400 <- 400
means400 <- rep (NA, iter)
for(i in 1:iter){
  means400[i] = mean(sample(ajstu, n.400))
}

n.900 <- 900
means900 <- rep (NA, iter)
for(i in 1:iter){
  means900[i] = mean(sample(ajstu, n.900))
}

n.1600 <- 1600
means1600 <- rep (NA, iter)
for(i in 1:iter){
  means1600[i] = mean(sample(ajstu, n.1600))
}

n.2500 <- 2500
means2500 <- rep (NA, iter)
for(i in 1:iter){
  means2500[i] = mean(sample(ajstu, n.2500))
}

h4 <- hist(means4)
h25 <- hist(means25)
h100 <- hist(means100)
h400 <- hist(means400)
h900 <- hist(means900)
h1600 <- hist(means1600)
h2500 <- hist(means2500)


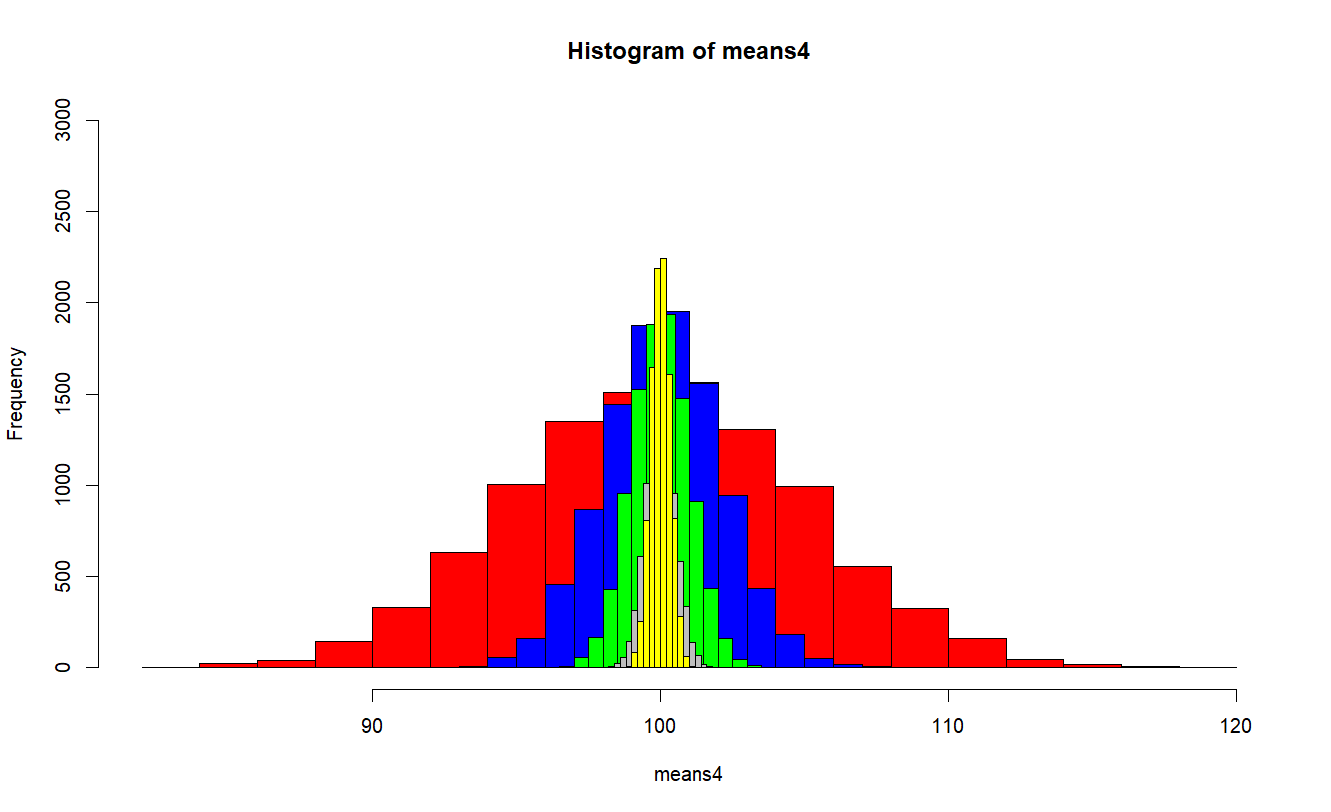
plot(h4, ylim=c(0,3000), col="red")
plot(h25, add = T, col="blue")
plot(h100, add = T, col="green")
plot(h400, add = T, col="grey")
plot(h900, add = T, col="yellow")


sss <- c(4,25,100,400,900,1600,2500) # sss sample sizes
ses <- rep (NA, length(sss)) # std errors
for(i in 1:length(sss)){
  ses[i] = sqrt(var(ajstu)/sss[i])
}
ses.means4 <- sqrt(var(means4))
ses.means25 <- sqrt(var(means25))
ses.means100 <- sqrt(var(means100))
ses.means400 <- sqrt(var(means400))
ses.means900 <- sqrt(var(means900))
ses.means1600 <- sqrt(var(means1600))
ses.means2500 <- sqrt(var(means2500))
ses.real <- c(ses.means4, ses.means25,
              ses.means100, ses.means400,
              ses.means900, ses.means1600,
              ses.means2500)
ses.real 

ses
se.1 <- ses
se.2 <- 2 * ses 

lower.s2 <- mean(ajstu)-se.2
upper.s2 <- mean(ajstu)+se.2
data.frame(cbind(sss, ses, ses.real, lower.s2, upper.s2))

min.value <- min(ajstu)
max.value <- max(ajstu)
min.value
max.value
# means25 분포에서 population의 가장 최소값인 
# min.value가 나올 확률은 얼마나 될까?
m.25 <- mean(means25)
sd.25 <- sd(means25)
m.25
sd.25
pnorm(min.value, m.25, sd.25)
# 위처럼 최소값, 최대값의 probability를 가지고
# 확률을 구하는 것은 의미가 없음. 즉, 어떤 샘플의
# 평균이 원래 population에서 나왔는지를 따지는 것을
# 그 pop의 최소값으로 판단하는 것은 의미가 없음.
# 그 보다는 sd.25와 같은 standard deviation을 가지
# 고 보는 것이 타당함. 이 standard deviation 을
# standard error라고 부름
se.25 <- sd.25
se.25.2 <- 2 * sd.25
mean(means25)+c(-se.25.2, se.25.2)
# 위처럼 95% certainty를 가지고 구간을 판단하거나
# 아래 처럼 점수를 가지고 probability를 볼 수도
# 있음
pnorm(95.5, m.25, sd.25)
# 혹은 
pnorm(95.5, m.25, sd.25) * 2
# 매우중요. 위의 이야기는 내가 25명의 샘플을 취
# 했을 때, 그 점수가 95.5가 나올 확률을 구해 본것
# 다른 예로
pnorm(106, m.25, sd.25, lower.tail = F)
# 혹은 
2 * pnorm(106, m.25, sd.25, lower.tail = F)

> # sampling distribution 
> n.ajstu <- 100000
> mean.ajstu <- 100
> sd.ajstu <- 10
> 
> set.seed(1024)
> ajstu <- rnorm2(n.ajstu, mean=mean.ajstu, sd=sd.ajstu)
> 
> mean(ajstu)
[1] 100
> sd(ajstu)
[1] 10
> var(ajstu)
     [,1]
[1,]  100
> min.value <- min(ajstu)
> max.value <- max(ajstu)
> min.value
[1] 57.10319
> max.value
[1] 141.9732
> 
> iter <- 10000 # # of sampling 
> 
> n.4 <- 4
> means4 <- rep (NA, iter)
> for(i in 1:iter){
+   means4[i] = mean(sample(ajstu, n.4))
+ }
> 
> n.25 <- 25
> means25 <- rep (NA, iter)
> for(i in 1:iter){
+   means25[i] = mean(sample(ajstu, n.25))
+ }
> 
> n.100 <- 100
> means100 <- rep (NA, iter)
> for(i in 1:iter){
+   means100[i] = mean(sample(ajstu, n.100))
+ }
> 
> n.400 <- 400
> means400 <- rep (NA, iter)
> for(i in 1:iter){
+   means400[i] = mean(sample(ajstu, n.400))
+ }
> 
> n.900 <- 900
> means900 <- rep (NA, iter)
> for(i in 1:iter){
+   means900[i] = mean(sample(ajstu, n.900))
+ }
> 
> n.1600 <- 1600
> means1600 <- rep (NA, iter)
> for(i in 1:iter){
+   means1600[i] = mean(sample(ajstu, n.1600))
+ }
> 
> n.2500 <- 2500
> means2500 <- rep (NA, iter)
> for(i in 1:iter){
+   means2500[i] = mean(sample(ajstu, n.2500))
+ }
> 
> h4 <- hist(means4)
> h25 <- hist(means25)
> h100 <- hist(means100)
> h400 <- hist(means400)
> h900 <- hist(means900)
> h1600 <- hist(means1600)
> h2500 <- hist(means2500)
> 
> 
> plot(h4, ylim=c(0,3000), col="red")
> plot(h25, add = T, col="blue")
> plot(h100, add = T, col="green")
> plot(h400, add = T, col="grey")
> plot(h900, add = T, col="yellow")
> 
> 
> sss <- c(4,25,100,400,900,1600,2500) # sss sample sizes
> ses <- rep (NA, length(sss)) # std errors
> for(i in 1:length(sss)){
+   ses[i] = sqrt(var(ajstu)/sss[i])
+ }
> ses.means4 <- sqrt(var(means4))
> ses.means25 <- sqrt(var(means25))
> ses.means100 <- sqrt(var(means100))
> ses.means400 <- sqrt(var(means400))
> ses.means900 <- sqrt(var(means900))
> ses.means1600 <- sqrt(var(means1600))
> ses.means2500 <- sqrt(var(means2500))
> ses.real <- c(ses.means4, ses.means25,
+               ses.means100, ses.means400,
+               ses.means900, ses.means1600,
+               ses.means2500)
> ses.real 
[1] 4.9719142 2.0155741 0.9999527 0.5034433 0.3324414
[6] 0.2466634 0.1965940
> 
> ses
[1] 5.0000000 2.0000000 1.0000000 0.5000000 0.3333333
[6] 0.2500000 0.2000000
> se.1 <- ses
> se.2 <- 2 * ses 
> 
> lower.s2 <- mean(ajstu)-se.2
> upper.s2 <- mean(ajstu)+se.2
> data.frame(cbind(sss, ses, ses.real, lower.s2, upper.s2))
   sss       ses  ses.real lower.s2 upper.s2
1    4 5.0000000 4.9719142 90.00000 110.0000
2   25 2.0000000 2.0155741 96.00000 104.0000
3  100 1.0000000 0.9999527 98.00000 102.0000
4  400 0.5000000 0.5034433 99.00000 101.0000
5  900 0.3333333 0.3324414 99.33333 100.6667
6 1600 0.2500000 0.2466634 99.50000 100.5000
7 2500 0.2000000 0.1965940 99.60000 100.4000
> 
> min.value <- min(ajstu)
> max.value <- max(ajstu)
> min.value
[1] 57.10319
> max.value
[1] 141.9732
> # means25 분포에서 population의 가장 최소값인 
> # min.value가 나올 확률은 얼마나 될까?
> m.25 <- mean(means25)
> sd.25 <- sd(means25)
> m.25
[1] 100.0394
> sd.25
[1] 2.015574
> pnorm(min.value, m.25, sd.25)
[1] 5.414963e-101
> # 위처럼 최소값, 최대값의 probability를 가지고
> # 확률을 구하는 것은 의미가 없음. 즉, 어떤 샘플의
> # 평균이 원래 population에서 나왔는지를 따지는 것을
> # 그 pop의 최소값으로 판단하는 것은 의미가 없음.
> # 그 보다는 sd.25와 같은 standard deviation을 가지
> # 고 보는 것이 타당함. 이 standard deviation 을
> # standard error라고 부름
> se.25 <- sd.25
> se.25.2 <- 2 * sd.25
> mean(means25)+c(-se.25.2, se.25.2)
[1]  96.00822 104.07051
> # 위처럼 95% certainty를 가지고 구간을 판단하거나
> # 아래 처럼 점수를 가지고 probability를 볼 수도
> # 있음
> pnorm(95.5, m.25, sd.25)
[1] 0.01215658
> # 혹은 
> pnorm(95.5, m.25, sd.25) * 2
[1] 0.02431317
> # 매우중요. 위의 이야기는 내가 25명의 샘플을 취
> # 했을 때, 그 점수가 95.5가 나올 확률을 구해 본것
> # 다른 예로
> pnorm(106, m.25, sd.25, lower.tail = F)
[1] 0.001551781
> # 혹은 
> 2 * pnorm(106, m.25, sd.25, lower.tail = F)
[1] 0.003103562
> 
> 
> 

위에서 standard deviation of sample means (샘플평균들로 이루어진 집합의 표준편차) 값을 standard error라고 부른다. 그리고 이 standard error 값은 원래 population의 $\sigma^2$ 값을 샘플의 사이즈로 나누어준 값을 ($\sigma^2/n$) 갖게 된다. 또한 이 샘플평균들의 집합의 평균은 (샘플평균들의 기대값, the mean of sample means) population의 평균값을 ($\mu$) 갖게 된다. 이에 대한 수학적 증명 문서는 mean and variance of the sample mean.

위를 이해한다면 이제 우리는 차이의가설을 만들어 테스트해볼 수 있다. hypothesis testing

모집단의 평균이 59