Table of Contents
You should read correlation, regression, multiple regression, and deriviation of a and b in a simple regression as well.
Covariance
Variance and Covariance
\begin{eqnarray}
\text{Var (X, X)} & = & \displaystyle \frac {SS}{df} \nonumber \\
& = & \displaystyle \frac {\sum{(\text{error})^2}}{n-1} \nonumber \\
& = & \displaystyle \frac {\sum_{i=1}^{n} {(X_i-\overline{X}}) (X_i-\overline{X}) } {n-1} \\
\text{Cov (X, Y)} & = & \displaystyle \frac {SP}{df} \nonumber \\
& = & \displaystyle \frac {\sum{(\text{product of errors from each mean})}}{n-1} \nonumber \\
& = & \displaystyle \frac {\sum_{i=1}^{n} {(X_i-\overline{X}}) (Y_i-\overline{Y}) } {n-1} \\
\end{eqnarray}
Note that
- covariance value can be negative.
- covariance value can be affected by the measurement unit
- e.g. Y = 억단위 투자금 vs Y = 원단위 투자금
- 큰 의미 없이 covariance 값이 달라진다.
- 이를 해결하기 위해서
- covariance value / each x and y unit measurement (sd)
Correlation
\begin{eqnarray} \text{correlation, r} & = & \frac {\text{Cov (X,Y)}} {sd(X) * sd(Y)} \\ & = & \frac {\text{SP (X,Y)} }{ \sqrt{\text{SS.x}*\text{SS.y}}} \nonumber \end{eqnarray}
F-test (anova)
for reminding
\begin{eqnarray*}
\text{F} & = & \frac {\text{MS}_\text{between group}} {\text{MS}_\text{within group}} \\
& = & \frac {\text{Difference due to the treatment (IV) } }{ \text{Difference due to random error} } \\
& = & \frac {\text{Difference explained by IV } }{ \text{Difference remained random} } \\
\text{R}^\text{2} & = & \frac {\text{SS}_\text{between}} {\text{SS}_\text{total} } \hfill \\
\end{eqnarray*}
Check in R
# data prep
rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
set.seed(191)
n.x <- 40
m.x <- 100
s.x <- 10
x <- rnorm2(n.x, m.x, s.x)
x
# y has a linear relationship with x
a <- 2
b <- -10
n.y <- n.x
re <- rnorm(n.y, 0, 20)
y <- (a*x) + b + re
y
# covariance x and y
cov(x,y)
sd(x)
sd(y)
# correlation coefficient
cov(x,y)/(sd(x)*sd(y))
cor(x,y)
n.x
df.x <- n.x-1
df.y <- df.x
sp.xy <- cov(x,y) * df.x # 혹은 아래처럼 구할 수 있다
sp.xy2 <- sum((x-m.x)*(y-m.y))
sp.xy == sp.xy2
ss.x <- var(x) * df.x
ss.y <- var(y) * df.y
sp.xy/sqrt(ss.x*ss.y)
cor(x,y)
Check in R: output
>
> # data prep
> rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
> set.seed(191)
> n.x <- 40
> m.x <- 100
> s.x <- 10
> x <- rnorm2(n.x, m.x, s.x)
> x
[,1]
[1,] 99.35817
[2,] 107.72169
[3,] 111.04574
[4,] 100.65968
[5,] 103.85350
[6,] 122.91296
[7,] 102.07927
[8,] 96.92756
[9,] 115.96195
[10,] 94.24901
[11,] 97.30033
[12,] 110.23739
[13,] 114.73077
[14,] 102.28326
[15,] 112.89297
[16,] 96.12475
[17,] 100.23641
[18,] 88.18567
[19,] 94.75283
[20,] 110.71928
[21,] 105.81396
[22,] 99.89274
[23,] 104.14215
[24,] 103.82149
[25,] 97.85588
[26,] 104.26732
[27,] 90.79210
[28,] 86.64193
[29,] 91.08626
[30,] 77.77150
[31,] 116.52461
[32,] 99.52034
[33,] 85.34661
[34,] 96.14854
[35,] 100.53925
[36,] 95.45190
[37,] 77.35589
[38,] 100.05830
[39,] 92.06457
[40,] 92.67148
attr(,"scaled:center")
[1] -0.08680858
attr(,"scaled:scale")
[1] 1.039345
>
> # y has a linear relationship with x
> a <- 2
> b <- -10
> n.y <- n.x
> re <- rnorm(n.y, 0, 20)
> y <- (a*x) + b + re
> y
[,1]
[1,] 175.7367
[2,] 200.0202
[3,] 241.0439
[4,] 166.0401
[5,] 195.5682
[6,] 210.8411
[7,] 181.9459
[8,] 193.8544
[9,] 225.4417
[10,] 182.5276
[11,] 194.5656
[12,] 232.4421
[13,] 255.3070
[14,] 209.0313
[15,] 219.1602
[16,] 181.7819
[17,] 214.3124
[18,] 187.2961
[19,] 207.3581
[20,] 235.0318
[21,] 199.2244
[22,] 208.1031
[23,] 182.2575
[24,] 201.4683
[25,] 169.6124
[26,] 173.7941
[27,] 161.0332
[28,] 152.1292
[29,] 153.4874
[30,] 147.7652
[31,] 189.2685
[32,] 188.5691
[33,] 155.5620
[34,] 172.8731
[35,] 184.9119
[36,] 183.3182
[37,] 119.8266
[38,] 162.6349
[39,] 170.0872
[40,] 150.7684
attr(,"scaled:center")
[1] -0.08680858
attr(,"scaled:scale")
[1] 1.039345
> cov(x,y)
[,1]
[1,] 222.3867
> sd(x)
[1] 10
> sd(y)
[1] 28.35979
> cov(x,y)/(sd(x)*sd(y))
[,1]
[1,] 0.7841619
> cor(x,y)
[,1]
[1,] 0.7841619
>
> n.x
[1] 40
> df.x <- n.x-1
> df.y <- df.x
> sp.xy <- cov(x,y) * df.x
> ss.x <- var(x) * df.x
> ss.y <- var(y) * df.y
> sp.xy/sqrt(ss.x*ss.y)
[,1]
[1,] 0.7841619
> cor(x,y)
[,1]
[1,] 0.7841619
>
>
code
rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
set.seed(191)
n.x <- 40
m.x <- 100
s.x <- 10
x <- rnorm2(n.x, m.x, s.x)
x
ss.x <- sum((m.x - x)^2)
df.x <- n.x - 1
ss.x/df.x
var(x)
# linear relationship
a <- 2
b <- -10
n.y <- n.x
re <- rnorm(n.y, 0, 20)
y <- (a*x) + b + re
y
m.y <- mean(y)
df.y <- n.y - 1
ss.y <- sum((y-m.y)^2)
ss.y/df.y
var(y)
#
prod <- (x-m.x)*(y-m.y)
sp <- sum(prod)
sp/df.y # covariance 값
cov(x,y) # covariance 펑션
s.x <- sd(x) # x변인에 대한 standard deviation 값
s.y <- sd(y) # y
(sp/df.y)/(s.x*s.y) # correlation 값
cor(x,y) # correlation 펑션
df.y
df.x
cov(x,y)/(s.x*s.y)
# covariance를 각각의 sd값을 곱한여 나눠 준 값이 r
(sp/df.y)/sqrt((ss.x/df.x)*(ss.y/df.y))
# 분모 분자에서 n-1을 제거하고 보면
sp/sqrt(ss.x*ss.y)
cor(x,y)
# graph with ggplot2
df <- data.frame(x,y)
library(ggplot2)
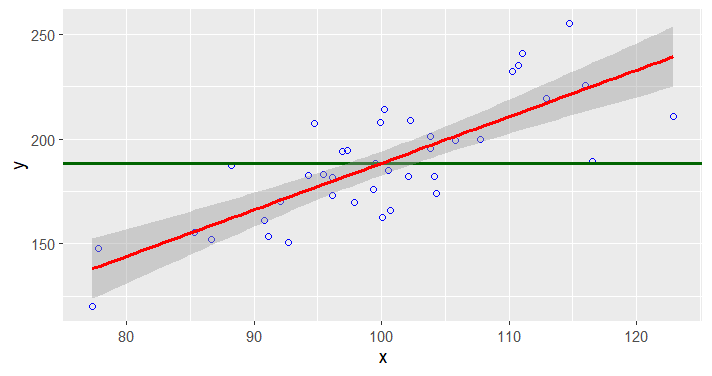
ggplot(data=df, aes(x,y)) +
geom_point(color="blue", size=1.5, pch=1.5) +
geom_hline(aes(yintercept=mean(y)), size=1, color="darkgreen") +
stat_smooth(method = "lm",
formula = y ~ x,
geom = "smooth", color="red", size=1)
# note that the red line is y.hat = a + bx,
# where error value y.hat - y is minimized
lm.df <- lm(y~x, data = df)
summary(lm.df)
a <- summary(lm.df)$coefficients[1]
b <- summary(lm.df)$coefficients[2]
a
b
# how to derive a and b
# how to derive coefficient values
# see wiki doc at
# http://commres.net/wiki/deriviation_of_a_and_b_in_a_simple_regression
b2 <- sp/ss.x
b3 <- cov(x,y)/var(x,x) # b2 == b3
# m.y = a + (b*m.x) 이므로
a2 <- m.y - (b2*m.x)
b3
b2
b
a2
a
#
# reg, res, total error
#
y.hat <- a+(b*x)
y.hat2 <- predict(lm.df)
head(y)
head(y.hat)
m.y
tmp <- data.frame(x, y, y.hat)
head(tmp)
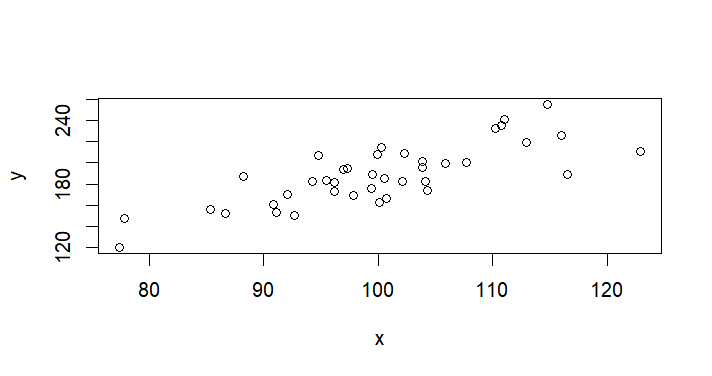
plot(x,y) # 원래 데이터
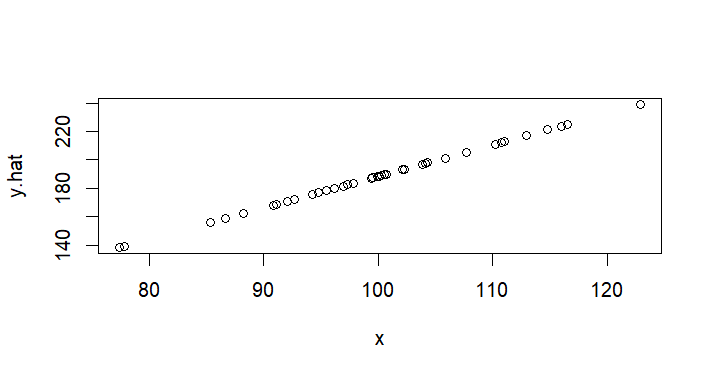
plot(x,y.hat) # 리그레션라인 예측선
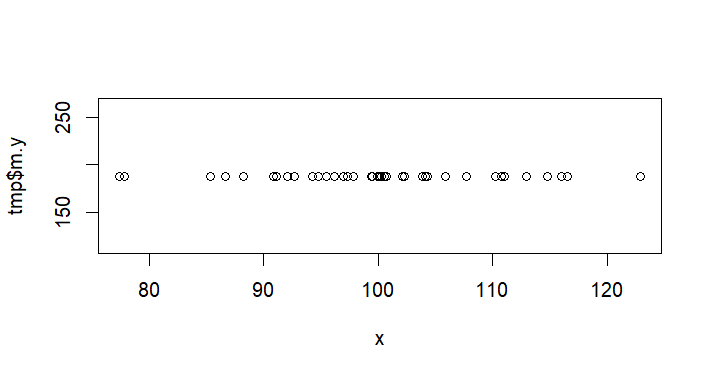
plot(x,tmp$m.y) # 평균 예측선
error <- y - y.hat
explained <- y.hat - m.y
tmp2 <- data.frame(tmp, explained, error)
head(tmp2)
head(y.hat == explained + m.y)
head(y == explained + error + m.y)
# note the below
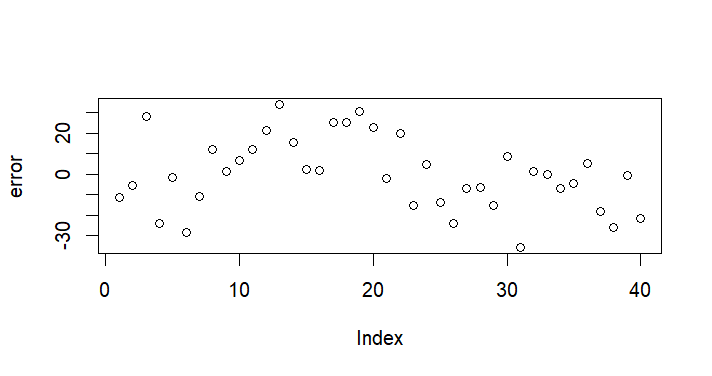
plot(error)
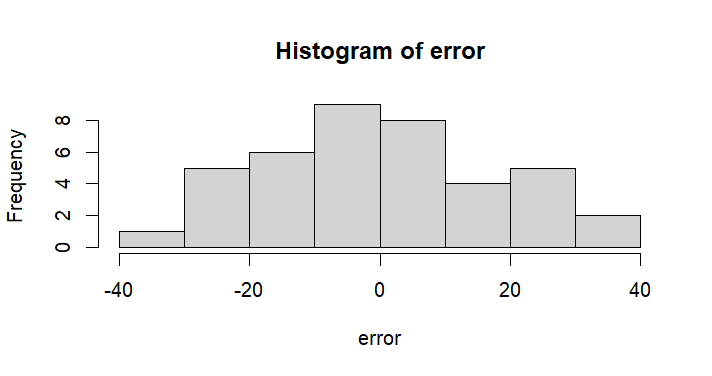
hist(error)
plot(x,error)
cor(x,error)
################
plot(x,explained)
cor(x,explained)
plot(x,(explained+m.y))
cor(x,(explained+m.y))
head(explained+error)
plot(x,(explained+error))
head(explained+error+m.y == y)
plot(x,(explained+error+m.y))
cor(x,(explained+error))
cor(x,(explained+error+m.y))
cor(x,y)
# see this also
round(cor(tmp2),3)
###############
# sum of square values
ss.res <- sum(error^2)
ss.reg <- sum(explained^2)
ss.y
ss.res
ss.reg
ss.res + ss.reg
# degrees of freedom values
k <- 2 # number of parameters
df.reg <- k - 1 # number of parameter estimation a and b (slope)
df.res <- n - df.reg - 1
ms.res <- ss.res/df.res
ms.reg <- ss.reg/df.reg
ss.reg
df.reg
ms.reg
ss.res
df.res
ms.res
# r square
ss.y
ss.reg
r.sq <- ss.reg/ss.y
r.sq
# 위의 r.sq 값이 충분히 컸는지를 알아보는 것은
# ss.reg가 충분히 컸는지를 알아보는 것
# 이는 IV, x가 y를 설명하는데 충분히 기여했는지
# 테스트하는 것. 이는 F-test를 이용해서 하게 된다
# F = MS.bet / MS.within
# regression의 경우는 F = MS.reg / MS.res
f.cal <- ms.reg/ms.res
f.cal
pf(f.cal, df.reg, df.res, lower.tail = F)
# check anova test
anova(lm.df)
summary(lm.df)
# standard error for b coefficient
# b coeffficient 값은 estimation
# n.y 개의 데이터에서 구한 coefficient값 b는
# 실제 x, y 모집단을 대표하는 b값은 위의
# estimation에서 standard error값을 구간으로 갖는
# 범위일 것.
res <- resid(lm.df)
data.frame(head(res))
data.frame(head(error))
se.b <- sqrt(ms.res/ss.x)
se.b
# as x increased by 1 unit, y would increase b +- 2se.b
b + c(-2*se.b, 2*se.b)
b
# to be exact
t.crit <- qt(.975, df.res)
t.crit
b + c(-t.crit*se.b, t.crit*se.b)
b
t.cal <- lm.df$coefficients[2]/se.b
t.cal
pt(t.cal, df.res, lower.tail = F)*2
pf(f.cal, df.reg, df.res, lower.tail = F)
# see also
t.cal
t.cal^2
f.cal
code output
> rnorm2 <- function(n,mean,sd){ mean+sd*scale(rnorm(n)) }
> set.seed(191)
> n.x <- 40
> m.x <- 100
> s.x <- 10
> x <- rnorm2(n.x, m.x, s.x)
> x
[,1]
[1,] 99.35817
[2,] 107.72169
[3,] 111.04574
[4,] 100.65968
[5,] 103.85350
[6,] 122.91296
[7,] 102.07927
[8,] 96.92756
[9,] 115.96195
[10,] 94.24901
[11,] 97.30033
[12,] 110.23739
[13,] 114.73077
[14,] 102.28326
[15,] 112.89297
[16,] 96.12475
[17,] 100.23641
[18,] 88.18567
[19,] 94.75283
[20,] 110.71928
[21,] 105.81396
[22,] 99.89274
[23,] 104.14215
[24,] 103.82149
[25,] 97.85588
[26,] 104.26732
[27,] 90.79210
[28,] 86.64193
[29,] 91.08626
[30,] 77.77150
[31,] 116.52461
[32,] 99.52034
[33,] 85.34661
[34,] 96.14854
[35,] 100.53925
[36,] 95.45190
[37,] 77.35589
[38,] 100.05830
[39,] 92.06457
[40,] 92.67148
attr(,"scaled:center")
[1] -0.08680858
attr(,"scaled:scale")
[1] 1.039345
> ss.x <- sum((m.x - x)^2)
> df.x <- n.x - 1
> ss.x/df.x
[1] 100
> var(x)
[,1]
[1,] 100
>
> # linear relationship
> a <- 2
> b <- -10
> n.y <- n.x
> re <- rnorm(n.y, 0, 20)
> y <- (a*x) + b + re
> y
[,1]
[1,] 175.7367
[2,] 200.0202
[3,] 241.0439
[4,] 166.0401
[5,] 195.5682
[6,] 210.8411
[7,] 181.9459
[8,] 193.8544
[9,] 225.4417
[10,] 182.5276
[11,] 194.5656
[12,] 232.4421
[13,] 255.3070
[14,] 209.0313
[15,] 219.1602
[16,] 181.7819
[17,] 214.3124
[18,] 187.2961
[19,] 207.3581
[20,] 235.0318
[21,] 199.2244
[22,] 208.1031
[23,] 182.2575
[24,] 201.4683
[25,] 169.6124
[26,] 173.7941
[27,] 161.0332
[28,] 152.1292
[29,] 153.4874
[30,] 147.7652
[31,] 189.2685
[32,] 188.5691
[33,] 155.5620
[34,] 172.8731
[35,] 184.9119
[36,] 183.3182
[37,] 119.8266
[38,] 162.6349
[39,] 170.0872
[40,] 150.7684
attr(,"scaled:center")
[1] -0.08680858
attr(,"scaled:scale")
[1] 1.039345
>
> m.y <- mean(y)
> df.y <- n.y - 1
> ss.y <- sum((y-m.y)^2)
> ss.y/df.y
[1] 804.2779
> var(y)
[,1]
[1,] 804.2779
>
> #
> prod <- (x-m.x)*(y-m.y)
> sp <- sum(prod)
> sp/df.y # covariance 값
[1] 222.3867
> cov(x,y) # covariance 펑션
[,1]
[1,] 222.3867
>
> s.x <- sd(x) # x변인에 대한 standard deviation 값
> s.y <- sd(y) # y
> (sp/df.y)/(s.x*s.y) # correlation 값
[1] 0.7841619
> cor(x,y) # correlation 펑션
[,1]
[1,] 0.7841619
>
> df.y
[1] 39
> df.x
[1] 39
>
> cov(x,y)/(s.x*s.y)
[,1]
[1,] 0.7841619
> # covariance를 각각의 sd값을 곱한여 나눠 준 값이 r
> (sp/df.y)/sqrt((ss.x/df.x)*(ss.y/df.y))
[1] 0.7841619
> # 분모 분자에서 n-1을 제거하고 보면
> sp/sqrt(ss.x*ss.y)
[1] 0.7841619
> cor(x,y)
[,1]
[1,] 0.7841619
>
> # graph with ggplot2
> df <- data.frame(x,y)
> library(ggplot2)
> ggplot(data=df, aes(x,y)) +
+ geom_point(color="blue", size=1.5, pch=1.5) +
+ geom_hline(aes(yintercept=mean(y)), size=1, color="darkgreen") +
+ stat_smooth(method = "lm",
+ formula = y ~ x,
+ geom = "smooth", color="red", size=1)
>
> # note that the red line is y.hat = a + bx,
> # where error value y.hat - y is minimized
>
> lm.df <- lm(y~x, data = df)
> summary(lm.df)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-35.880 -11.932 -0.458 12.199 34.148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -33.9867 28.6879 -1.185 0.243
x 2.2239 0.2855 7.790 2.16e-09 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 17.83 on 38 degrees of freedom
Multiple R-squared: 0.6149, Adjusted R-squared: 0.6048
F-statistic: 60.68 on 1 and 38 DF, p-value: 2.157e-09
> a <- summary(lm.df)$coefficients[1]
> b <- summary(lm.df)$coefficients[2]
> a
[1] -33.98667
> b
[1] 2.223867
> # how to derive a and b
> # how to derive coefficient values
> # see wiki doc at
> # http://commres.net/wiki/deriviation_of_a_and_b_in_a_simple_regression
> b2 <- sp/ss.x
> b3 <- cov(x,y)/var(x,x) # b2 == b3
> # m.y = a + (b*m.x) 이므로
> a2 <- m.y - (b2*m.x)
>
> b3
[,1]
[1,] 2.223867
> b2
[1] 2.223867
> b
[1] 2.223867
>
> a2
[1] -33.98667
> a
[1] -33.98667
>
> #
> # reg, res, total error
> #
> y.hat <- a+(b*x)
> y.hat2 <- predict(lm.df)
> head(y)
[,1]
[1,] 175.7367
[2,] 200.0202
[3,] 241.0439
[4,] 166.0401
[5,] 195.5682
[6,] 210.8411
> head(y.hat)
[,1]
[1,] 186.9727
[2,] 205.5720
[3,] 212.9643
[4,] 189.8671
[5,] 196.9697
[6,] 239.3554
> m.y
[1] 188.4
>
> tmp <- data.frame(x, y, y.hat)
> head(tmp)
x y y.hat
1 99.35817 175.7367 186.9727
2 107.72169 200.0202 205.5720
3 111.04574 241.0439 212.9643
4 100.65968 166.0401 189.8671
5 103.85350 195.5682 196.9697
6 122.91296 210.8411 239.3554
> plot(x,y) # 원래 데이터
> plot(x,y.hat) # 리그레션라인 예측선
> plot(x,tmp$m.y) # 평균 예측선
>
> error <- y - y.hat
> explained <- y.hat - m.y
> tmp2 <- data.frame(tmp, explained, error)
> head(tmp2)
x y y.hat explained error
1 99.35817 175.7367 186.9727 -1.427352 -11.235956
2 107.72169 200.0202 205.5720 17.172003 -5.551819
3 111.04574 241.0439 212.9643 24.564266 28.079646
4 100.65968 166.0401 189.8671 1.467035 -23.826982
5 103.85350 195.5682 196.9697 8.569671 -1.401474
6 122.91296 210.8411 239.3554 50.955365 -28.514250
>
> head(y.hat == explained + m.y)
[,1]
[1,] TRUE
[2,] TRUE
[3,] TRUE
[4,] TRUE
[5,] TRUE
[6,] TRUE
> head(y == explained + error + m.y)
[,1]
[1,] TRUE
[2,] TRUE
[3,] TRUE
[4,] TRUE
[5,] TRUE
[6,] TRUE
>
> # note the below
> plot(error)
> hist(error)
> plot(x,error)
> cor(x,error)
[,1]
[1,] 7.981058e-17
> ################
> plot(x,explained)
> cor(x,explained)
[,1]
[1,] 1
> plot(x,(explained+m.y))
> cor(x,(explained+m.y))
[,1]
[1,] 1
>
> head(explained+error)
[,1]
[1,] -12.663308
[2,] 11.620185
[3,] 52.643911
[4,] -22.359948
[5,] 7.168197
[6,] 22.441115
> plot(x,(explained+error))
> head(explained+error+m.y == y)
[,1]
[1,] TRUE
[2,] TRUE
[3,] TRUE
[4,] TRUE
[5,] TRUE
[6,] TRUE
> plot(x,(explained+error+m.y))
>
> cor(x,(explained+error))
[,1]
[1,] 0.7841619
> cor(x,(explained+error+m.y))
[,1]
[1,] 0.7841619
> cor(x,y)
[,1]
[1,] 0.7841619
> # see this also
> round(cor(tmp2),3)
x y y.hat explained error
x 1.000 0.784 1.000 1.000 0.000
y 0.784 1.000 0.784 0.784 0.621
y.hat 1.000 0.784 1.000 1.000 0.000
explained 1.000 0.784 1.000 1.000 0.000
error 0.000 0.621 0.000 0.000 1.000
> ###############
>
> # sum of square values
> ss.res <- sum(error^2)
> ss.reg <- sum(explained^2)
> ss.y
[1] 31366.84
> ss.res
[1] 12079.06
> ss.reg
[1] 19287.78
> ss.res + ss.reg
[1] 31366.84
>
> # degrees of freedom values
> k <- 2 # number of parameters
> df.reg <- k - 1 # number of parameter estimation a and b (slope)
> df.res <- n - df.reg - 1
> ms.res <- ss.res/df.res
> ms.reg <- ss.reg/df.reg
>
> ss.reg
[1] 19287.78
> df.reg
[1] 1
> ms.reg
[1] 19287.78
>
> ss.res
[1] 12079.06
> df.res
[1] 38
> ms.res
[1] 317.87
>
> # r square
> ss.y
[1] 31366.84
> ss.reg
[1] 19287.78
> r.sq <- ss.reg/ss.y
> r.sq
[1] 0.6149098
> # 위의 r.sq 값이 충분히 컸는지를 알아보는 것은
> # ss.reg가 충분히 컸는지를 알아보는 것
> # 이는 IV, x가 y를 설명하는데 충분히 기여했는지
> # 테스트하는 것. 이는 F-test를 이용해서 하게 된다
> # F = MS.bet / MS.within
> # regression의 경우는 F = MS.reg / MS.res
> f.cal <- ms.reg/ms.res
> f.cal
[1] 60.67819
> pf(f.cal, df.reg, df.res, lower.tail = F)
[1] 2.157284e-09
> # check anova test
> anova(lm.df)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 19288 19287.8 60.678 2.157e-09 ***
Residuals 38 12079 317.9
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> summary(lm.df)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-35.880 -11.932 -0.458 12.199 34.148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -33.9867 28.6879 -1.185 0.243
x 2.2239 0.2855 7.790 2.16e-09 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 17.83 on 38 degrees of freedom
Multiple R-squared: 0.6149, Adjusted R-squared: 0.6048
F-statistic: 60.68 on 1 and 38 DF, p-value: 2.157e-09
>
> # standard error for b coefficient
> # b coeffficient 값은 estimation
> # n.y 개의 데이터에서 구한 coefficient값 b는
> # 실제 x, y 모집단을 대표하는 b값은 위의
> # estimation에서 standard error값을 구간으로 갖는
> # 범위일 것.
>
> res <- resid(lm.df)
> data.frame(head(res))
head.res.
1 -11.235956
2 -5.551819
3 28.079646
4 -23.826982
5 -1.401474
6 -28.514250
> data.frame(head(error))
head.error.
1 -11.235956
2 -5.551819
3 28.079646
4 -23.826982
5 -1.401474
6 -28.514250
> se.b <- sqrt(ms.res/ss.x)
> se.b
[1] 0.285491
> # as x increased by 1 unit, y would increase b +- 2se.b
> b + c(-2*se.b, 2*se.b)
[1] 1.652885 2.794849
> b
[1] 2.223867
>
> # to be exact
> t.crit <- qt(.975, df.res)
> t.crit
[1] 2.024394
> b + c(-t.crit*se.b, t.crit*se.b)
[1] 1.645921 2.801813
> b
[1] 2.223867
>
> t.cal <- lm.df$coefficients[2]/se.b
> t.cal
x
7.789621
>
>
> pt(t.cal, df.res, lower.tail = F)*2
x
2.157284e-09
> pf(f.cal, df.reg, df.res, lower.tail = F)
[1] 2.157284e-09
>
> # see also
> t.cal
x
7.789621
> t.cal^2
x
60.67819
> f.cal
[1] 60.67819
>
>