Table of Contents
See anova, repeated measure anova
Factorial ANOVA
t-test와 ANOVA의 섹션까지 다룬것은 모두 하나의 독립변인(Independent Variable)과 하나의 종속변인(Dependent Variable) 간의 관계에 대한 규명을 하는 것이었다.
실제 연구를 하는 경우 이와 같이 하나씩의 독립변인과 종속변인으로 이루어진 검증을 하기보다는 여러가지 다른 원인을 종합적으로 살펴보는 때가 많다. 즉, 연구자는 실험참가자의 행동이나 반응으로 나타나는 종속변인의 원인을 하나의 독립변인이 아닌 여러가지 (대개는 2가지) 독립변인을 놓고 살펴본다는 것이다.
이와 같은 연구를 Factorial Design이라고 한다.
2개의 독립변인과 하나의 종속변인으로 이루어진 디자인이라면 Two-factor design이라고 부를 수 있다.
예
여름에는 작업 능률이 떨어진다고 한다. 덥기 때문이다. 그러나, 종종 사람들은 더운 것은 참을 수 있으나 습도가 높은 것은 참을 수 없다고 한다. 즉, 작업능률을 저하하는데 작용하는 (영향을 미치는) 요소로 2가지가 포함될 수 있다. 하나는 온도이고 하나는 습도이다. 아래 표는 이를 위한 실험에 대한 결과를 표로 요약한 것이다. 표가 의미하는 것은 이 연구가 6개의 특별한 상황 (2가지의 독립변인으로 인해서 일어나는)에 따른 작업능률의 (한가지의 종속변인) 변화에 대한 파악이다.
| Factor B: Temperature | |||||
|---|---|---|---|---|---|
| 24 | 29 | 34 | |||
| Factor A: Humidity | 30% | n=15 24도 30% | n=15 29도 30% | n=15 34도 30% | n30=45 $\overline{X_{30_{\\\%}}} = ? $ |
| 70% | n=15 24도 70% | n=15 29도 70% | n=15 34도 70% | n70=45 $ \overline{X_{70_{\\\%}}} = ? $ |
|
| n24=30 $ \overline{X_{24^{c}}} = ? $ | n29=30 $ \overline{X_{29^{c}}} = ? $ | n34=30 $ \overline{X_{34^{c}}} = ? $ | |||
위의 상황에서 독립변인의 분석을 한다고 하면, 연구자가 관심을 갖고 살펴보게 되는 부분으로
- 습도의 변화 (2가지, 30%와 70%)에 따른 차이
- 온도의 변화 (3가지, 24, 29, 34도)에 따른 차이
- 위의 두 가지 변화로 설명되지 않는다고 나타나는 차이 (만약에 존재한다면) = 즉, 두 가지 독립변인의 동시존재에 의해서만 나타나는 차이
를 보는 것이 된다. 따라서, 가설테스트의 입장에서 보면, 연구자는 한가지 문제에 대한 3가지 가설을 테스트하는 것이 된다. 이를 풀어서 이야기 하자면, 1) 습도의 영향력 2) 온도의 영향력 3) 두가지가 동시존재함으로써 나타나는 영향력 에 대한 테스트이다.
얼뜻 보면, 복잡한듯 하지만, 위의 테스트 또한 F-test ([ANOVA])를 이용하여 해결할 수 있으며, 이는 아래와 같이 나타낼 수 있다.
$$F = \frac{\text{variance (differences) \\ between sample means}}{\text{variance (difference) expected by chance}} \cdots [1]$$
위의 식 [1]이 F값이 크다는 것은 샘플 간의 차이가 랜덤하게 나타나는 차이에 비해 상대적으로 크다는 것을 의미한다. 이 차이가 통계학적으로 유의미한 정도로 크다고 판단하기 위해서는 ANOVA에서 본 것과 같이 F-ratio테이블을 이용하게 된다.
주효과 (Main effects)
| Factor B: Temperature | |||||
|---|---|---|---|---|---|
| Factor A: Humidity | 24 | 29 | 34 | ||
| 30% | $ \overline{X}=85 $ | $ \overline{X}=80 $ | $ \overline{X}=75 $ | $ \overline{X}=80 $ | |
| 70% | $ \overline{X}=75 $ | $ \overline{X}=70 $ | $ \overline{X}=65 $ | $ \overline{X}=70 $ | |
| $ \overline{X}=80 $ | $ \overline{X}=75 $ | $ \overline{X}=70 $ | |||
Factor A: Humidity에 관한 가설은 아래와 같이 정리된다:
$$\text{H1: } \mu_{A_1} \neq \mu_{A_2}$$
이에 대한 영가설은:
$$\text{H1: } \mu_{A_1} = \mu_{A_2}$$
이에 대한 F-test는
$$F = \frac{\text{variance (difference) between the means for the factor A}}{\text{variance (difference) expected by chance}}$$
$$F = \frac{\text{variance (difference) between row means}}{\text{variance (difference) expected by chance}}$$
와 같이 정리할 수 있다.
반면에, Factor B: Temperature에 관한 가설은:
$\text{H1: } \mu_{B_1} \neq \mu_{B_2} $ 혹은
$\text{H1: } \mu_{B_2} \neq \mu_{B_3} $ 혹은
$\text{H1: } \mu_{B_1} \neq \mu_{B_3} $ 혹은
$\text{H1: } \mu_{B_1} \neq \mu_{B_2} \neq \mu_{B_3} $
와 같이 정리될 수 있는데, 한가지 현상에 대한 가설을 여러번에 나누어서 설명하는 것은 복잡하므로 아래와 같이 요약해 볼 수 있다.
H1: 적어도 한 평균값이 다른 평균값과 다를 것이다.
이에 대한 영가설은 비교적 쉽게 표현된다:
$\text{H1: } \mu_{B_1} = \mu_{B_2} = \mu_{B_3}$
다시, 이에 대한 F-test는
$$F = \frac{\text{variance (difference) between the means for the factor B}}{\text{variance (difference) expected by chance}}$$
$$F = \frac{\text{variance (difference) between column means}}{\text{variance (difference) expected by chance}}$$
와 같이 정리할 수 있다.
즉, 연구자는 각 독립변인의 특성에 대한 그룹의 분산 간 차이를 비교하여 봄으로써, 각각의 팩터(독립변인)의 효과를 살펴볼 수 있다. 이를 각각 Factor A에 대한 주효과 (Main effect)와 Factor B에 대한 주효과 (Main effect)라고 이야기 할 수 있다.
상호효과 (Interaction effects)
아래의 테이블은 위의 실험결과를 약간 변형한 것인데, 각각의 독립변인 (팩터)에 대한 평균값은 이전의 테이블과 동일하다.
| Factorial ANOVA | |||||
|---|---|---|---|---|---|
| Factor B: Temperature | |||||
| Factor A: Humidity | 24 | 29 | 34 | ||
| 30% | $ \overline{X}=80 $ | $ \overline{X}=80 $ | $ \overline{X}=80 $ | $ \overline{X}=80 $ | |
| 70% | $ \overline{X}=80 $ | $ \overline{X}=70 $ | $ \overline{X}=60 $ | $ \overline{X}=70 $ | |
| $ \overline{X}=80 $ | $ \overline{X}=75 $ | $ \overline{X}=70 $ | |||
여기서 주의해서 보아야 할 점은 첫번째 열에서의 평균인 80점은 각 셀의 점수인 80점의 평균으로 온도의 차이에 의한 영향력이 없다는 것을 의미한다. 그러나, 두번째 열을 채우는 셀의 값들은 10점씩의 차이를 보이고 있다. 이 차이가 온도에 의한 것이라고 이야기 하자면, 30%의 습도 상태에서는 이 차이가 보이질 않았다는 것이 문제가 된다. 다른 말로 표현하자면, 온도에 의한 차이를 보기 위해서는 습도가 관건이 된다는 것이다. 또 다르게 표현하자면, 온도에 의한 차이가 나타난 것은 습도의 상태와 서로 엮여서만 나타나는 것처럼 보이는 것이다. 이와 같이 차이에 대한 해석에 있어서 오직 한 상태(독립변인)의 영향력으로만 설명할 수 없는 상황을 해석할 때, '상호효과(interaction effect)'가 있다고 이야기 한다. 이를 다시 이야기 하자면, 'B의 효과는 A와 상호의존적인 상태'라고 할 수 있다.
이를 다시 F-test의 공식에 적용시켜서 정리해보면:
$$F = \frac{\text{variance (mean difference) not explained by main effects}}{\text{variance (difference) expected by chance}}$$
와 같다.
이를 가설로 정리를 해보자면
H1: A팩터와 B팩터 간의 상호작용이 존재한다. 즉, 각각의 상태에 따라서 나타나는 평균의 차이가 두 팩터가 갖는 주효과에 의해서만 설명되지 않고 부가적으로 더 있다.
H0: A팩터와 B팩터 간의 상호작용은 존재하지 않는다. 즉, 각각의 상태에 따라서 나타나는 평균의 차이는 두 팩터가 갖는 주효과에 의해서만 설명된다.
와 같이 정리할 수 있다.
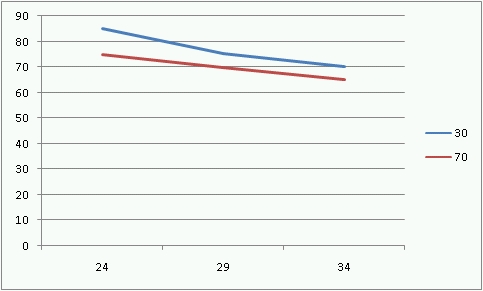
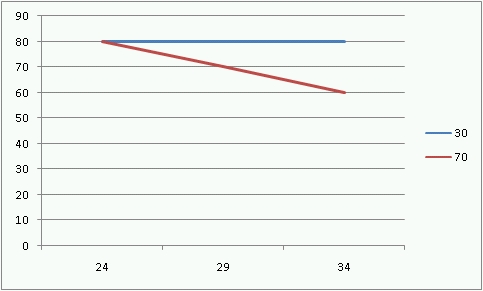
그러나, 사실 위의 표의 해석이 그리 직관적이지는 않다. 상호의존적이라는 단어가 의미하는 것이 그리 직관적이지 않기 때문이다. 이럴 경우, 흔히 연구자는 위의 표를 아래와 같은 도표로 바꾸어 살펴보게 되는데, 이렇게 하는 이유는 상호효과(InteractionEffect)의 존재여부가 완연히 들어나기 때문이다.
그림1과 2의 붉은색선과 푸른색선은 각각 습도의 차이(30%와 70%)를 나타내며 x축은 온도의 차이를 나타낸다. 1의 경우, 두 선은 서로 평행하여 겹치지 않는데 이것이 의미하는 것은 두 요인의 영향력이 서로 독립적으로 나타난다는 뜻이다. 반면에 오른쪽의 그림2는 두선이 평행하지 않는데, 이는 두 요인이 상호의존적으로 작용하기 때문이다. 이 경우에는 온도의 영향은 오직 습도가 높을때에만 나타난다.
e.g.,
| Main effect for factor A but no main effect for factor B | ||||
|---|---|---|---|---|
| B1 | B2 | |||
| A1 | 20 | 20 | MA1 = 20 | 10-point difference |
| A2 | 10 | 10 | MA2 = 10 | |
| MB1 = 15 | MB2 = 15 | |||
| No difference | ||||
| Main effect for both factor A and factor B | ||||
|---|---|---|---|---|
| B1 | B2 | |||
| A1 | 10 | 30 | MA1 = 20 | 10-point difference |
| A2 | 20 | 40 | MA2 = 30 | |
| MB1 = 15 | MB2 = 35 | |||
| 20-point difference | ||||
| No main effect for either factor A and factor B | ||||
|---|---|---|---|---|
| B1 | B2 | |||
| A1 | 10 | 20 | MA1 = 15 | no difference |
| A2 | 20 | 10 | MA2 = 15 | |
| MB1 = 15 | MB2 = 15 | |||
| no difference | ||||
2 Factor ANOVA test
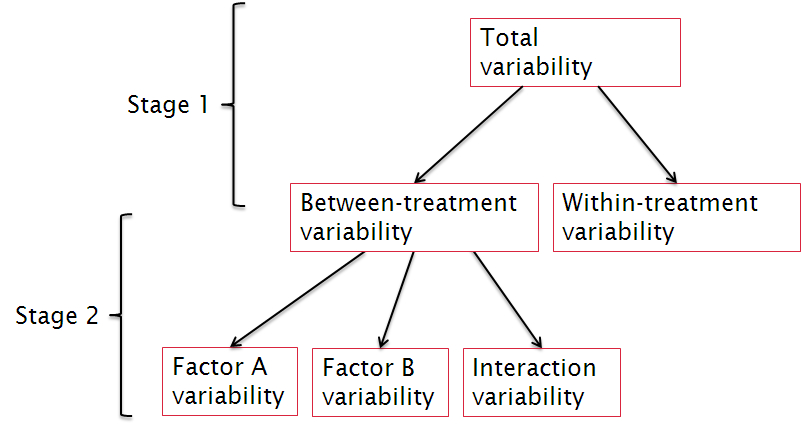
Factorial ANOVA계산은 다음과 같이 쪼개어 볼 수 있다. 우선 첫 단계는 이전의 ANOVA와 같은 단계이다. 즉, Between-variability와 Within-variability를 구해서 그 비율을 보는 것을 말한다. 두번째 단계에서는 각각의 요인(factor)에 대한 variability의 정도와 상호효과(interaction)의 정도를 알아보는 단계이다. 이 단계에서 3가지의 F-비율(F-ratio)을 구한다. 각 요인의 분산정도(variability)를 알기 위해서는 각 요인의 between-treatment 분산정도를 알아야 하고, 또한 within-treatment의 분산정도를 알아야 한다. 언제나 그랬듯이 분산은 다음과 같이 구한다.
$$\text{mean square} = \text{MS} = \frac{SS}{df}$$
실제로 2 Factor F-ratio를 구하는 방법은 단일(single) Factor F-ratio를 구하는 것과 동일하다.
| Factor B | ||||||
|---|---|---|---|---|---|---|
| Factor A | $B_1$ | $B_2$ | $B_3$ | $N=30$ $G=120$ $\Sigma{X^2}=840$ |
||
| $A_1$ | 3 | 2 | 9 | $T_{A_1} = 90$ | ||
| 1 | 5 | 9 | ||||
| 1 | 9 | 13 | ||||
| 6 | 7 | 6 | ||||
| 4 | 7 | 8 | ||||
| T=15 | T=30 | T=45 | ||||
| SS=18 | SS=28 | SS=26 | ||||
| $A_2$ | 0 | 3 | 0 | $T_{A_2} = 30$ | ||
| 2 | 8 | 0 | ||||
| 0 | 3 | 0 | ||||
| 0 | 3 | 5 | ||||
| 3 | 3 | 0 | ||||
| T=5 | T=20 | T=5 | ||||
| SS=8 | SS=20 | SS=20 | ||||
| $T_{B_1}=20$ | $T_{B_2}=50$ | $T_{B_3}=50$ | ||||
Stage 1
Total variability
$$SS_{total}=\Sigma{X^2}-\frac{G^2}{N}$$
\begin{eqnarray} SS_{total} & = & 840-\frac{120^2}{30} \nonumber \\ & = & 840-480 \nonumber \\ & = & 360 \nonumber \end{eqnarray}
$$df_{total}= N - 1$$
$$df_{total}= 29$$
Between variability
$$SS_{\text{between}}=\Sigma{\frac{T^2}{n}}-\frac{G^2}{N}$$
\begin{eqnarray} SS_{\text{between}} & = & { \frac{15^2}{5} + \frac{30^2}{5} + \frac{45^2}{5} + \frac{5^5}{5} + \frac{20^5}{5} + \frac{5^5}{5} - \frac{120^2}{30} } \nonumber \\ & = & 45 + 180 + 405 + 5 + 80 + 5 - 480 \nonumber \\ & = & 720 - 480 \nonumber \\ & = & 240 \nonumber \end{eqnarray}
\begin{eqnarray} df_{between} & = & k - 1 \nonumber \\ & = & \text{number of cells} - 1 \nonumber \\ & = & 5 \nonumber \end{eqnarray}
Within variability
\begin{eqnarray} SS_{within} & = & \Sigma{SS_{each \; treatment}} \nonumber \\ & = & 18 + 28 + 26 + 8 + 20 + 20 \nonumber \\ & = & 120 \nonumber \end{eqnarray}
\begin{eqnarray} df_{within} & = & \Sigma{df_{each \; treatment}} \nonumber \\ & = & 4 + 4 + 4 + 4 + 4 + 4 \nonumber \\ & = & 24 \nonumber \end{eqnarray}
Check
$$SS_{total} = SS_{between} + SS_{within}$$
$$df_{total} = df_{between} + df_{within}$$
Stage 2
1. For factor A.
$$SS_{between \; As} = SS_A = \Sigma{\frac{{T_A}^2}{n_A}} - \frac{G^2}{N}$$
\begin{eqnarray} SS_{A} & = & \frac{90^2}{15} + \frac{30^2}{15} - \frac{120^2}{30} \nonumber \\ & = & 540 + 60 - 480 \nonumber \\ & = & 120 \nonumber \end{eqnarray}
위의 표에서,
$$df=df_{A}=\text{number of levels of A} -1 $$
\begin{eqnarray} df_{\text{between As}} = df_A = \text{(number of levels of As)} - 1 = 1 \nonumber \end{eqnarray}
2. For factor B.
$$SS_{between \; Bs} = SS_B = \Sigma{\frac{{T_B}^2}{n_B}} - \frac{G^2}{N}$$
\begin{eqnarray} SS_{B} & = & \frac{20^2}{10} + \frac{50^2}{10} + \frac{50^2}{10} - \frac{120^2}{30} \nonumber \\ & = & 40 + 250 + 250 - 480 \nonumber \\ & = & 60 \nonumber \end{eqnarray}
$$df=df_{B}=\text{number of levels of B} -1 $$
\begin{eqnarray} df_{\text{between Bs}} = df_B = \text{(number of levels of Bs)} - 1 = 2 \nonumber \end{eqnarray}
3. For interaction (A X B).
$$SS_{A X B} = SS_{between} - SS_A - SS_B $$
\begin{eqnarray} SS_{A X B} & = & 240 - 120 - 60 \nonumber \\ & = & 60 \nonumber \end{eqnarray}
$$df_{A X B} = df_{between} - df_A - df_B $$
$$df_{A X B} = 5 - 1 - 2 = 2 $$
And,
$$MS_{within} = \frac{SS_{within}}{df_{within}}$$
$$MS_{within} = \frac{120}{24} = 5 $$
$$MS_A = \frac{SS_A}{df_A} = \frac{120}{1} $$
$$MS_B = \frac{SS_B}{df_B} = \frac{60}{2} $$
$$MS_{AXB} = \frac{SS_{AXB}}{df_{AXB}} = \frac{60}{2} $$
Finally,
$$ F_A (1, 24) = \frac{MS_A}{MS_{within}} = \frac{120}{5} = 24 $$
$$ F_B (2, 24) = \frac{MS_B}{MS_{within}} = \frac{30}{5} = 6 $$
$$ F_{AXB} (2, 24) = \frac{MS_{AXB}}{MS_{within}} = \frac{30}{5} = 6 $$
Check F distribution table
$$ F_{crit} (1, 24) = 4.26 $$
$$ F_{crit} (2, 24) = 3.40 $$
$$ F_{crit} (2, 24) = 3.40 $$
Check
| Factor B: Temperature | ||||
|---|---|---|---|---|
| Factor A | B1 | B2 | B3 | |
| A1 | n=10 T=0 SS=30 | n=10 T=10 SS=40 | n=10 T=20 SS=50 |
|
| A2 | n=10 T=40 SS=60 | n=10 T=30 SS=50 | n=10 T=20 SS=40 |
|
- Calculate the totals for each level of factor A, and compute SS for factor A.
- Calculate the totals for factor B, and compute SS for the factor
- Given that the between-treatments SS is equal to 100, what is the SS for the interaction?
- Calculate the within-treatments SS, df, and MS for these data.
예 1
detergent.csv
detergent 는 세탁의 정도를 세제의 종류와 물온도를 독립변인으로 (팩터로) 가설검증을 한 것이다. 데이터는 위의 detergent.csv 이다. 또한 손으로 Factorial ANOVA를 하기 위해 이 데이터를 엑셀에 정리하여 detergent.anova.by.hand.xlsx로 올려 두었다.
de <- read.csv("http://commres.net/wiki/_media/detergent.csv", sep = ",", header=T)
de
de$type <- factor(de$type, level=c(1,2), label=c("super", "best"))
de$w.temp <- factor(de$w.temp, level=c(1,2,3), label=c("cold", "warm", "hot"))
de
de.anova <- aov(cleanness ~ type * w.temp, data=de)
summary(de.anova)
with(de, interaction.plot(x.factor=type,
trace.factor=w.temp, response=cleanness,
fun=mean, type="b", legend=T,
ylab="cleanness", main="Interaction Plot (type by temp)",
pch=c(1,19)))
> de <- read.csv("http://commres.net/wiki/_media/detergent.csv", sep = ",", header=T)
> de
type w.temp cleanness
1 1 1 4
2 1 1 5
3 1 1 6
4 1 1 5
5 2 1 6
6 2 1 6
7 2 1 4
8 2 1 4
9 1 2 7
10 1 2 9
11 1 2 8
12 1 2 10
13 2 2 13
14 2 2 15
15 2 2 12
16 2 2 12
17 1 3 10
18 1 3 12
19 1 3 11
20 1 3 9
21 2 3 12
22 2 3 13
23 2 3 10
24 2 3 13
> de$type <- factor(de$type, level=c(1,2), label=c("super", "best"))
> de$w.temp <- factor(de$w.temp, level=c(1,2,3), label=c("cold", "warm", "hot"))
> de
type w.temp cleanness
1 super cold 4
2 super cold 5
3 super cold 6
4 super cold 5
5 best cold 6
6 best cold 6
7 best cold 4
8 best cold 4
9 super warm 7
10 super warm 9
11 super warm 8
12 super warm 10
13 best warm 13
14 best warm 15
15 best warm 12
16 best warm 12
17 super hot 10
18 super hot 12
19 super hot 11
20 super hot 9
21 best hot 12
22 best hot 13
23 best hot 10
24 best hot 13
> de.anova <- aov(cleanness ~ type * w.temp, data=de)
> summary(de.anova)
Df Sum Sq Mean Sq F value Pr(>F)
type 1 24 24.00 15.43 0.000986 ***
w.temp 2 193 96.50 62.04 8.41e-09 ***
type:w.temp 2 21 10.50 6.75 0.006496 **
Residuals 18 28 1.56
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> with(de, interaction.plot(x.factor=type,
+ trace.factor=w.temp, response=cleanness,
+ fun=mean, type="b", legend=T,
+ ylab="cleanness", main="Interaction Plot (type by temp)",
+ pch=c(1,19)))
>
>
만약에 손으로 계산했다면 R에서
de <- read.csv("http://commres.net/wiki/_media/detergent.csv", sep = ",", header=T)
de
de$type <- factor(de$type, level=c(1,2), label=c("super", "best"))
de$w.temp <- factor(de$w.temp, level=c(1,2,3), label=c("cold", "warm", "hot"))
de
de.typenova <- aov(cleanness ~ type * w.temp, data=de)
summary(de.typenova)
with(de, interaction.plot(x.factor=type,
trace.factor=w.temp, response=cleanness,
fun=mean, type="b", legend=T,
ylab="cleanness", main="Interaction Plot (type by temp)",
pch=c(1,19)))
attach(de)
table(type, w.temp)
n.sub <- length(cleanness)
n.type.group <- 2
n.w.temp.group <- 3
tapply(cleanness, list(type, w.temp), mean) # 각 셀에서의 평균
df.within.each <- tapply(cleanness, list(type, w.temp), length) -1 # 각 셀에서의 샘플숫자
n.within.each <- df.within.each + 1
df.within <- sum(df.within.each) # df within
var.within <- tapply(cleanness, list(type, w.temp), var) # var.within
ss.within.each <- tapply(cleanness, list(type, w.temp), var) * df.within.each
ss.within.each
ss.within <- sum(ss.within.each) # ss.within
ss.within
interaction.plot(type, w.temp, cleanness)
mean.type <- tapply(cleanness, list(type), mean)
mean.w.temp <- tapply(cleanness, list(w.temp), mean)
mean.type
mean.w.temp
var.type <- tapply(cleanness, list(type), var)
var.w.temp <- tapply(cleanness, list(w.temp), var)
mean.tot <- mean(cleanness)
var.tot <- var(cleanness)
n.sub <- length(cleanness)
df.tot <- n.sub - 1
ss.tot <- var.tot * df.tot
## between
mean.each <- tapply(cleanness, list(type, w.temp), mean)
mean.each
mean.tot <- mean(cleanness)
mean.tot
n.each <- tapply(cleanness, list(type, w.temp), length)
n.each
n.type.each <- tapply(cleanness, list(type), length)
n.w.temp.each <- tapply(cleanness, list(w.temp), length)
ss.w.bet <- sum(n.each*(mean.each-mean.tot)^2)
ss.w.bet
ss.tot
ss.within
ss.w.bet
ss.w.bet + ss.within
ss.type <- sum(n.type.each * ((mean.tot - mean.type)^2))
ss.w.temp <- sum(n.w.temp.each * ((mean.tot - mean.w.temp)^2))
ss.type
ss.w.temp
ss.type.w.temp <- ss.w.bet - (ss.type + ss.w.temp)
ss.type.w.temp
ss.tot
ss.w.bet
ss.within
ss.type
ss.w.temp
ss.type.w.temp
df.tot <- n.sub - 1
df.w.bet <- (n.type.group * n.w.temp.group) - 1
df.type <- n.type.group - 1
df.w.temp <- n.w.temp.group - 1
df.type.w.temp <- df.w.bet - (df.type + df.w.temp)
df.within <- sum(df.within.each)
df.tot
df.w.bet
df.type
df.w.temp
df.type.w.temp
df.within
ms.type <- ss.type / df.type
ms.w.temp <- ss.w.temp / df.w.temp
ms.type.w.temp <- ss.type.w.temp / df.type.w.temp
ms.within <- ss.within / df.within
ms.type
ms.w.temp
ms.type.w.temp
ms.within
f.type <- ms.type / ms.within
f.w.temp <- ms.w.temp / ms.within
f.type.w.temp <- ms.type.w.temp / ms.within
alpha <- .05
# confidence interval
ci <- 1 - alpha
f.type
# 봐야할 F분포표에서의 F-value
# qt 처럼 qf 사용
# qf(alpha, df.w.between, df.within, lower.tail=F) 처럼 사용
qf(ci, df.type, df.within)
# 혹은
# qf(alpha, df.type, df.within, lower.tail = F)
# 도 마찬가지
pf(f.type, df.type, df.within, lower.tail = F)
f.w.temp
qf(ci, df.w.temp, df.within)
pf(f.w.temp, df.w.temp, df.within, lower.tail = F)
f.type.w.temp
qf(ci, df.type.w.temp, df.within)
pf(f.type.w.temp, df.type.w.temp, df.within, lower.tail = F)
# aov result
summary(de.typenova)
예 2. cookie experiment
- anovadata.sav SPSS 데이터
| Factor B: Fullness | |||||
|---|---|---|---|---|---|
| Factor A: Weight | Empty | Full | |||
| Normal | n=20 $\overline{X}=22$ T=440 SS=1502 | n=20 $\overline{X}$ =15 T=300 SS=940 | $T_\text{obese}=740$ | ||
| Obese | n=20 $\overline{X}$ = 17 T=340 SS=1062 | n=20 $\overline{X}$ = 18 T=360 SS=1084 | $T_\text{normal} = 700$ | ||
| $T_\text{empty} =780$ | $T_\text{full} = 660$ | G=1440 N=80 $\Sigma{X^2}=31028$ |
|||
$SS_{total}=\Sigma{X^2}-\frac{G^2}{N}$
$SS_{\text{between}}=\Sigma{\frac{T^2}{n}}-\frac{G^2}{N}$
$SS_{\text{within}} = \Sigma{SS_{\text{each treatment}}} $
$df_{\text{between}} = k - 1$
$df_{\text{within}} = \Sigma{df_{each \; treatment}} $
$SS_{total} = SS_{between} + SS_{within}$
$df_{total} = df_{between} + df_{within}$
For factor A.
$SS_{between \; As} = SS_A = \Sigma{\frac{{T_A}^2}{n_A}} - \frac{G^2}{N}$
$SS_{between \; Bs} = SS_B = \Sigma{\frac{{T_B}^2}{n_B}} - \frac{G^2}{N}$
$SS_{A X B} = SS_{between} - SS_A - SS_B $
$df=df_{A}=\text{number of levels of A} -1 $
$df=df_{B}=\text{number of levels of B} -1 $
$df_{A X B} = df_{between} - df_A - df_B $
And,
$MS_{within} = \frac{SS_{within}}{df_{within}}$
$MS_A = \frac{SS_A}{df_A} = $
$MS_B = \frac{SS_B}{df_B} = $
$MS_{AXB} = \frac{SS_{AXB}}{df_{AXB}} = $
step 1. Build hypotheses
step 2. Locate the critical range for F-ratio. calculate the $dfs$
- $df_{total}$
- $df_{within}$
- $df_{between}$
- $df_A$
- $df_B$
- $df_{AxB}$
Compute F-ratio
SS
- $SS_{total}$
$\overline{X_{t}}= 18 $
$\overline{X_{t}}^2= 324 $
$N = 80 $
$N*(\overline{X_t}^2) = 25920 $
$\Sigma{X^2} - \frac{(G^2)}{N} = 31028 - 25920 = 5108$
- $SS_{within}$
- $SS_{within} = \Sigma{SS_{within}} = 1502 + 940 + 1062 + 1084 = 4588$
- $SS_{between}$
- $SS_{between} = 5108 - 4588 = 520 $
- $SS_A$
- $SS_B$
- $SS_{\text{AxB}}$
MS
- $MS_{A}$
- $MS_{B}$
- $MS_{\text{AxB}}$
- $MS_{Within}$
F-ratio
- $F_{A}$
- $F_{B}$
- $F_{\text{AxB}}$
Tests of Between-Subjects Effects
Dependent Variable: nCookies
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. |
| Corrected Model | 520.000a | 3 | 173.333 | 2.871 | .042 |
| Intercept | 25920.000 | 1 | 25920.000 | 429.364 | .000 |
| Weight | 20.000 | 1 | 20.000 | .331 | .567 |
| Fullness | 180.000 | 1 | 180.000 | 2.982 | .088 |
| Weight * Fullness | 320.000 | 1 | 320.000 | 5.301 | .024 |
| Error | 4588.000 | 76 | 60.368 | ||
| Total | 31028.000 | 80 | |||
| Corrected Total | 5108.000 | 79 | |||
| a R Squared = .102 (Adjusted R Squared = .066) | |||||
데이터 파일
cookies.csv
손으로 계산하기
cookies.xlsx
cookies <- read.csv("http://commres.net/wiki/_media/cookies.csv")
cookies
str(cookies)
cookies$weight = factor(cookies$weight, levels=c(1,2), labels=c("normal","obese"))
cookies$fullness = factor(cookies$fullness, levels=c(1,2), labels=c("empty","full"))
str(cookies)
cookies
with(cookies, interaction.plot(x.factor=fullness,
trace.factor=weight, response=ncookies,
fun=mean, type="b", legend=T,
ylab="num of cookies", main="Interaction Plot",
pch=c(1,19)))
cookies.aov <- aov(ncookies ~ weight * fullness, data=cookies)
summary(cookies.aov)
> cookies <- read.csv("http://commres.net/wiki/_media/cookies.csv")
> cookies
weight fullness ncookies
1 1 1 15
2 1 1 17
3 1 1 32
4 1 1 12
5 1 1 34
6 1 1 27
7 1 1 13
8 1 1 24
9 1 1 41
10 1 1 20
11 1 1 23
12 1 1 25
13 1 1 9
14 1 1 21
15 1 1 22
16 1 1 26
17 1 1 26
18 1 1 28
19 1 1 22
20 1 1 3
21 1 2 22
22 1 2 7
23 1 2 15
24 1 2 6
25 1 2 8
26 1 2 18
27 1 2 24
28 1 2 19
29 1 2 11
30 1 2 9
31 1 2 24
32 1 2 19
33 1 2 9
34 1 2 19
35 1 2 29
36 1 2 9
37 1 2 18
38 1 2 17
39 1 2 3
40 1 2 14
41 2 1 7
42 2 1 19
43 2 1 8
44 2 1 23
45 2 1 6
46 2 1 11
47 2 1 18
48 2 1 23
49 2 1 22
50 2 1 16
51 2 1 28
52 2 1 19
53 2 1 2
54 2 1 27
55 2 1 20
56 2 1 25
57 2 1 23
58 2 1 10
59 2 1 19
60 2 1 14
61 2 2 14
62 2 2 21
63 2 2 16
64 2 2 14
65 2 2 17
66 2 2 20
67 2 2 20
68 2 2 21
69 2 2 32
70 2 2 26
71 2 2 9
72 2 2 14
73 2 2 16
74 2 2 15
75 2 2 6
76 2 2 5
77 2 2 12
78 2 2 23
79 2 2 27
80 2 2 32
>
> str(cookies)
'data.frame': 80 obs. of 3 variables:
$ weight : int 1 1 1 1 1 1 1 1 1 1 ...
$ fullness: int 1 1 1 1 1 1 1 1 1 1 ...
$ ncookies: int 15 17 32 12 34 27 13 24 41 20 ...
>
> cookies$weight = factor(cookies$weight, levels=c(1,2), labels=c("normal","obese"))
> cookies$fullness = factor(cookies$fullness, levels=c(1,2), labels=c("empty","full"))
>
> str(cookies)
'data.frame': 80 obs. of 3 variables:
$ weight : Factor w/ 2 levels "normal","obese": 1 1 1 1 1 1 1 1 1 1 ...
$ fullness: Factor w/ 2 levels "empty","full": 1 1 1 1 1 1 1 1 1 1 ...
$ ncookies: int 15 17 32 12 34 27 13 24 41 20 ...
>
> cookies
weight fullness ncookies
1 normal empty 15
2 normal empty 17
3 normal empty 32
4 normal empty 12
5 normal empty 34
6 normal empty 27
7 normal empty 13
8 normal empty 24
9 normal empty 41
10 normal empty 20
11 normal empty 23
12 normal empty 25
13 normal empty 9
14 normal empty 21
15 normal empty 22
16 normal empty 26
17 normal empty 26
18 normal empty 28
19 normal empty 22
20 normal empty 3
21 normal full 22
22 normal full 7
23 normal full 15
24 normal full 6
25 normal full 8
26 normal full 18
27 normal full 24
28 normal full 19
29 normal full 11
30 normal full 9
31 normal full 24
32 normal full 19
33 normal full 9
34 normal full 19
35 normal full 29
36 normal full 9
37 normal full 18
38 normal full 17
39 normal full 3
40 normal full 14
41 obese empty 7
42 obese empty 19
43 obese empty 8
44 obese empty 23
45 obese empty 6
46 obese empty 11
47 obese empty 18
48 obese empty 23
49 obese empty 22
50 obese empty 16
51 obese empty 28
52 obese empty 19
53 obese empty 2
54 obese empty 27
55 obese empty 20
56 obese empty 25
57 obese empty 23
58 obese empty 10
59 obese empty 19
60 obese empty 14
61 obese full 14
62 obese full 21
63 obese full 16
64 obese full 14
65 obese full 17
66 obese full 20
67 obese full 20
68 obese full 21
69 obese full 32
70 obese full 26
71 obese full 9
72 obese full 14
73 obese full 16
74 obese full 15
75 obese full 6
76 obese full 5
77 obese full 12
78 obese full 23
79 obese full 27
80 obese full 32
>
> with(cookies, interaction.plot(x.factor=fullness,
+ trace.factor=weight, response=ncookies,
+ fun=mean, type="b", legend=T,
+ ylab="num of cookies", main="Interaction Plot",
+ pch=c(1,19)))
>
> cookies.aov <- aov(ncookies ~ weight * fullness, data=cookies)
> summary(cookies.aov)
Df Sum Sq Mean Sq F value Pr(>F)
weight 1 20 20.0 0.331 0.5666
fullness 1 180 180.0 2.982 0.0883 .
weight:fullness 1 320 320.0 5.301 0.0241 *
Residuals 76 4588 60.4
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
Interpreting interaction
위에서 두개 독립변인에 대한 주효과가 없었으므로 각 독립변인의 종류 (특성) 별로 어디에서 차이가 났는가를 살피는 것은 의미가 없음. 따라서 아래는 필요한 절차가 아님.
> TukeyHSD(cookies.aov, which="weight")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = ncookies ~ weight * fullness, data = cookies)
$weight
diff lwr upr p adj
2-1 -1 -4.460253 2.460253 0.5665956
> TukeyHSD(cookies.aov, which="fullness")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = ncookies ~ weight * fullness, data = cookies)
$fullness
diff lwr upr p adj
2-1 -3 -6.460253 0.4602531 0.088274
See also example 5 in Twoway ANOVA in R
e.g.,
| Influence of urine chemicals to other male & female rats | ||||
|---|---|---|---|---|
| Factor B: Amount of chemical | ||||
| None | Small | Large | ||
| Factor A: gender | Male | n=5 T=10 SS=15 | n=5 T=20 SS=19 | n=5 T=30 SS=31 |
| Female | n=5 T=10 SS=15 | n=5 T=20 SS=19 | n=5 T=30 SS=31 |
|
| $\Sigma{X^2} = 460 $ | ||||
Build hypotheses. Use ANOVA with critical level = .05 to test the researcher's hypotheses.