COMMunication
RESearch.NET

User Tools

Site Tools

You are here: index » repeated_measure_anova
Trace: • repeated_measure_anova
repeated_measure_anova

Table of Contents

See also, ANOVA, Factorial ANOVA, paired sample t-test repeated_measures_anova

Repeated Measure ANOVA

Introduction

  • one-way ANOVA for related, not-independent groups
  • extension of the dependent t-test (one group t-test, repeated measure t-test)
  • also, it is called “within-subjects ANOVA” or “ANOVA for correlated samples”
  • the simplest one is one-way repeated measures ANOVA
  • which requires one independent and one dependent variable
  • the independent variable is categorical (either nominal or ordinal)
  • the dependent variable is continuous (interval or ratio)

Test Circumstances

  • one subject with repeated measures across a time period (differences of mean scores across three or more time periods)
    • participants being tested with headache drugs such as
      • group A, B, C, placebo
      • across the time periods j, k, l, m
    • testing the effect of a three-month exercise training program on blood sugar level
      • measure blood sugar level at 3 different points (pre-exercise, midway, post-exercise)
  • one subject with repeated measures in different situation (treatments; differences of mean scores under three or more different conditions)
    • e.g., participant (n=30) using and evaluating three web site UI (naver, daum, and google)
    • and rate its usefulness, usability and ease of use
  • data should look as follows:
pre-excerise
“sugar level” 		mid-term
“sugar level” 		post-exercise
“sugar level”
a 250 220 150
b 300 170 120
c 150 120 120
d 230 170 160
e 260 250 250
level 1 level 2 level 3

Levels = related groups of the independent variable “time”

treatment
condition
“naver” 		treatment
condition
“daum” 		treatment
condition
“google”
a 70 60 80
b 50 70 50
c 40 50 60
d 30 40 60
e 60 50 40
level 1 level 2 level 3

in general, the data should look

time/condition
T1 T2 T3
s1 s1 s1 s1
s2 s2 s2 s2
s3 s3 s3 s3
s4 s4 s4 s4
s5 s5 s5 s5
.. .. .. ..
sn sn sn sn

You should discern the above from normal ANOVA situation.

group treatment
a 1 70
b 1 50
c 1 40
d 1 30
e 1 60
f 2 60
g 2 70
h 2 50
i 2 40
j 2 50
k 3 80
l 3 50
m 3 60
n 3 60
o 3 40

LOGICS

  • $\text{independent ANOVA: } F = \displaystyle \frac{MS_{between}}{MS_{within}} = \frac{MS_{between}}{MS_{error}}$
  • $\text{rep measures ANOVA: } F = \displaystyle \frac{MS_{between}}{MS_{within}} = \displaystyle \frac{MS_{conditions}}{MS_{error}}$

주>

  • “between” 이란 단어는 독립적인 그룹 간의 비교를 의미하므로, 반복측정(repeated measure)의 경우에는 conditions라는 용어를 사용.

– Picture about here –

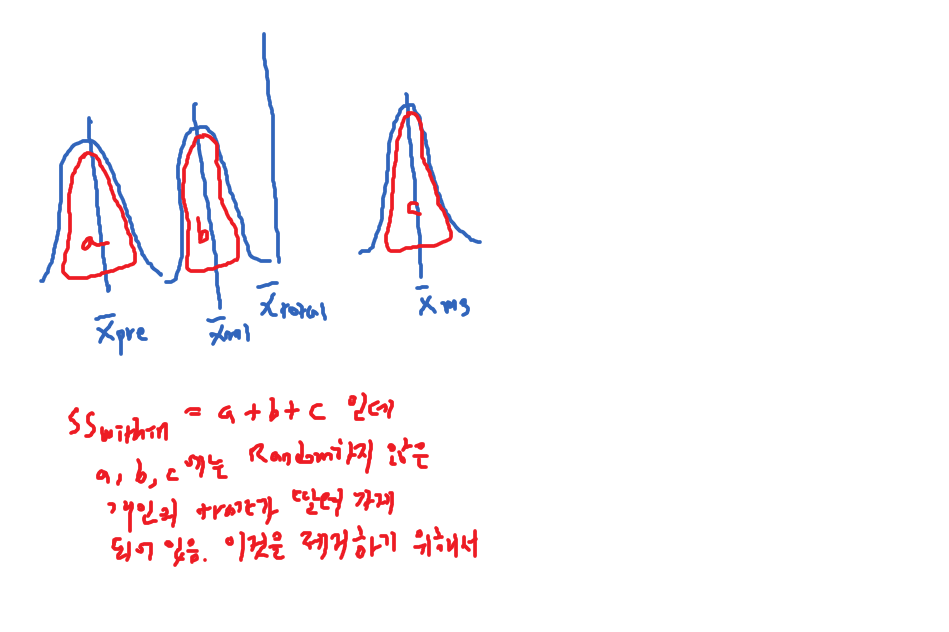
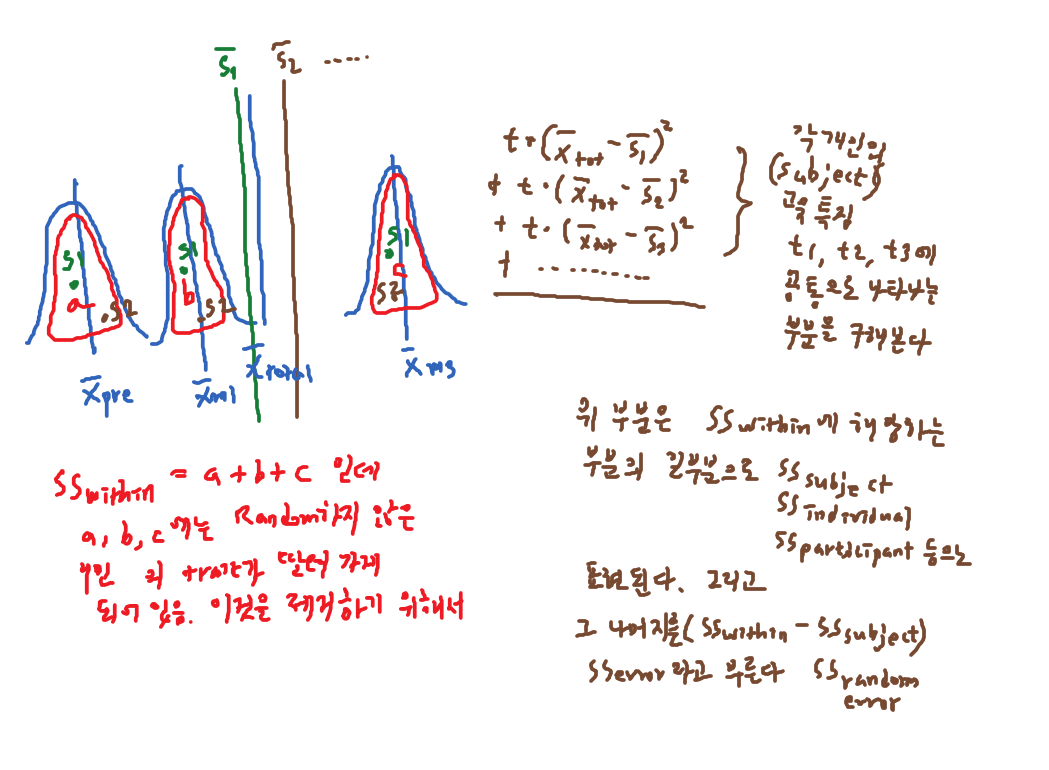
  • but, $\text{SS}_\text{{within}}$ can be partitioned as
    • $\text{SS}_{\text{ subjects}}$ and $\text{SS}_{\text{ error}}$
    • that is, some of the “within variation” are carried along in each individual.
    • Among the two, we can exclude the first from SSwithin
    • and solely use the latter as SSerror
    • This is to say:
      • in $\text{independent ANOVA: } \text{SS}_\text{{within}} = \text{SS}_{\text{error}} $
      • in $\text{rep measures ANOVA: } \text{SS}_\text{{within}} = \text{SS}_{\text{subjects}} + \text{SS}_{\text{error}}$
    • This means that the term SSerror will be smaller
    • But, with this SSerror, the df is going to be (n-1)(k-1)
subjects Pre 1 Month 3 Month Subject
Means
1 45 50 55 50
2 42 42 45 43
3 36 41 43 40
4 39 35 40 38
5 51 55 59 55
6 44 49 56 49.7
Monthly mean 42.8 45.3 49.97
Grand mean: 45.9

We do this (and the below example) with an excel spreadsheet, repeated_measures_anova_eg.xlsx.
We also require fdistribution table to determine the null hypothesis test.

Headache Analysis
base treatment average
per case
(subject,
participant)
ser w1 w2 w3 w4 w5 $\overline{X}_{part}$
= average
per case
(subject,
participant)
1 21 22 8 6 6 12.6
2 20 19 10 4 9 12.4
3 7 5 5 4 5 5.2
4 25 30 13 12 4 16.8
5 30 33 10 8 6 17.4
6 19 27 8 7 4 13
7 26 16 5 2 5 10.8
8 13 4 8 1 5 6.2
9 26 24 14 8 17 17.8
average
per week 		20.78 20.00 9.00 5.78 6.78 $\overline{X}$ = 12.47
Stats
Mean Total 12.47
$\Sigma{X_i}$ 561
$\Sigma{{X_i}^2}$ 10483
# of week 5
# of case (n) 9

SStotal = $\Sigma{(X-\overline{X})^2} $ = 3489.2

SSbetween
= SSconditions
= SSweeks
= $n\Sigma{(\overline{X}_{week} - \overline{X})^2}$ = 1934.5

SSwithin
= $ \Sigma \Sigma{(X_{s_i.t_j} - \overline{X_{t_j}})^2}$
= $ \Sigma (411.6, 836.0, 78.0, 93.6, 135.6) $
= 1554.7

SSparticipants = $w\Sigma{(\overline{X}_{participants}-\overline{X})^2}$ = 833.6

SSresidual
= SSerror
= SSwithin - SSparticipants
= 1554.7 - 833.6
= 721.1

OR
SSresidual =
= SSerror
= (SStotal - SSweeks(between)) - SSparticipants
= 721.1



dftotal = N - 1 = 45 - 1 = 44

dfweek = 5 - 1 = 4 = dfbetween

dfparticipants = 9 - 1 = 8 = dfsubjects

dferror= (n - 1)(k - 1) = 8 * 4 = 32 = 40 - 8 = 32

dfwithin = N - k = 45 - 5 = 40

ie

시각적 인지점수
참가자 No visual distraction Visual distraction Sound Distraction
A 47 22 41
B 57 31 52
C 38 18 40
D 45 32 43

in r

demo1

https://rcompanion.org/handbook/I_09.html

data files in e.gs:
demo1.csv
demo2.csv
demo3.csv
demo4.csv
exer.csv 

demo1  <- read.csv("https://stats.idre.ucla.edu/stat/data/demo1.csv")
demo1 
str(demo1) ## 모든 변인이 int이므로 (숫자) factor로 바꿔야 한다

## Convert variables to factor
demo1 <- within(demo1, {
  group <- factor(group)
  time <- factor(time)
  id <- factor(id)
}) ## 이제 pulse만 제외하고 모두 factor로 변환된 데이터

str(demo1)

demo1 data는 아래와 같다. 

id	group	pulse	time
1	1	10	1
1	1	10	2
1	1	10	3
2	1	10	1
2	1	10	2
2	1	10	3
3	1	10	1
3	1	10	2
3	1	10	3
4	1	10	1
4	1	10	2
4	1	10	3
5	2	15	1
5	2	15	2
5	2	15	3
6	2	15	1
6	2	15	2
6	2	15	3
7	2	16	1
7	2	15	2
7	2	15	3
8	2	15	1
8	2	15	2
8	2	15	3

이를 정리해보면

time
t1 t2 t3 mean
of the
same person's
measures
1 10 10 10 10
2 10 10 10 10
3 10 10 10 10
4 10 10 10 10
5 15 15 15 15
6 15 15 15 15
7 16 15 15 15.333
8 15 15 15 15
mean
across
the time 		12.625 12.5 12.5 12.542 
demo1.within.only.aov <- aov(pulse ~ time + Error(id), data = demo1)
summary(demo1.within.only.aov)
> demo1.within.only.aov <- aov(pulse ~ time + Error(id), data = demo1)
> summary(demo1.within.only.aov)

Error: id
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals  7  155.3   22.18               

Error: Within
          Df Sum Sq Mean Sq F value Pr(>F)
time       2 0.0833 0.04167       1  0.393
Residuals 14 0.5833 0.04167               
>

see repeated_measures_anova_eg.xlsx

demo 2

see repeated measure anova

Twoway repeated measure anova

see twoway repeated measure anova

reference

repeated_measure_anova.txt · Last modified: by hkimscil
Donate Powered by PHP Valid HTML5 Valid CSS Driven by DokuWiki