Table of Contents
interaction effects in regression analysis
- see also ANCOVA
E.g. 1 One category and one continuous
Data 만들기
x<-runif(50,0,10)
f1<-gl(n=2,k=25,labels=c("Low","High"))
modmat<-model.matrix(~x*f1,data.frame(f1=f1,x=x))
coeff<-c(1,3,-2,1.5)
y<-rnorm(n=50,mean=modmat%*%coeff,sd=0.5)
dat<-data.frame(y=y,f1=f1,x=x)
dat
mod <- lm(y~x*f1)
summary(mod)
library(ggplot2)
library(jtools) # in case not loading, install.packages("jtools")
library(interactions)
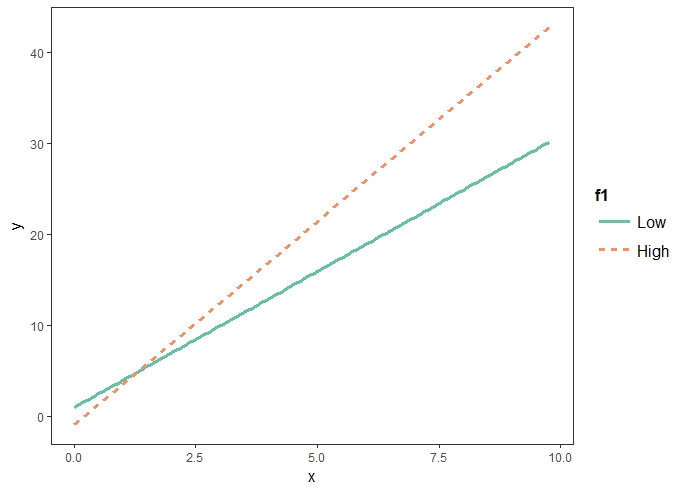
interact_plot(mod, pred = "x", modx = "f1", plot.points = TRUE)
> x<-runif(50,0,10)
> f1<-gl(n=2,k=25,labels=c("Low","High"))
> modmat<-model.matrix(~x*f1,data.frame(f1=f1,x=x))
> coeff<-c(1,3,-2,1.5)
> y<-rnorm(n=50,mean=modmat%*%coeff,sd=0.5)
> dat<-data.frame(y=y,f1=f1,x=x)
작물의 무게가 온도와 토양의 질소에 영향을 받을까? 라는 연구문제에서 추출된 데이터. 작물무게에 대한 질소함유량의 영향과 온도의 영향, 그리고 그 두 변인의 상호작용효과에 대해서 알고 싶다.
> head(dat)
y f1 x
1 21.8693480 Low 7.128280776
2 9.9550750 Low 3.085331542
3 10.9473336 Low 3.535275350
4 17.1011539 Low 5.611984141
5 7.1786120 Low 1.734487077
6 20.9093423 Low 6.526126855
> mod <- lm(y~x*f1)
> summary(mod)
Residuals:
Min 1Q Median 3Q Max
-0.9627 -0.2945 -0.1238 0.3386 0.9835
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.35817 0.17959 7.563 1.31e-09 ***
x 2.95059 0.03187 92.577 < 2e-16 ***
f1High -2.63301 0.25544 -10.308 1.54e-13 ***
x:f1High 1.59598 0.04713 33.867 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4842 on 46 degrees of freedom
Multiple R-squared: 0.9983, Adjusted R-squared: 0.9981
F-statistic: 8792 on 3 and 46 DF, p-value: < 2.2e-16
regression formula: y hat ~ 1.35817 + 2.95059*x + -2.63301*f1High + 1.59598*x:f1High x: 질소 f1: High | Low
- when f1High = 0,
y hat ~ 1.35817 + 2.95059*x- x변인(질소)이 0인 상태일 때의 작물의 무게가 1.3g정도 된다는 것을 말한다.
- 다음의 x는 x변인(질소)의 단위가 1씩 증가할 때마다 작물의 무게는 2.9씩 증가한다는 것을 말한다. (일반적인 regression line 해석)
- when f1High = 1,
y hat ~ 1.35817 + 2.95059*x + -2.63301*(1) + 1.59598*x:(1)y hat ~ 1.35817 + -2.63301*(1) + 2.95059*x + 1.59598*x:(1)y hat ~ -1.27493 + 4.54657x- x:f1High는 온도가 High일경우에 x의 영향력이 1.59 더 많다는 것을 말한다 (1.59598*x:(1)).
- 즉, x의 기울기(slope)는 온도에 따라서 변하는데, 온도가 높은 상태일 경우에 2.90 + 1.59 = 4.54임을 말한다.
- 또한 온도가 높을 상태일 때의 절편은 -1.27493 가 된다.
library(ggplot2)
library(jtools) # in case not loading, install.packages("jtools")
interact_plot(mod, pred = "x", modx = "f1")
Two category variables
> set.seed(12)
> f1<-gl(n=2,k=30,labels=c("Low","High"))
> f2<-as.factor(rep(c("A","B","C"),times=20))
> modmat<-model.matrix(~f1*f2,data.frame(f1=f1,f2=f2))
> coeff<-c(1,3,-2,-4,1,-1.2)
> y<-rnorm(n=60,mean=modmat%*%coeff,sd=0.1)
> dat<-data.frame(y=y,f1=f1,f2=f2)
> dat
y f1 f2
1 0.8519432 Low A
2 -0.8422831 Low B
3 -3.0956744 Low C
4 0.9079995 Low A
5 -1.1997642 Low B
6 -3.0272296 Low C
7 0.9684651 Low A
8 -1.0628255 Low B
9 -3.0106464 Low C
10 1.0428015 Low A
11 -1.0777720 Low B
12 -3.1293882 Low C
13 0.9220433 Low A
14 -0.9988048 Low B
15 -3.0152416 Low C
16 0.9296536 Low A
17 -0.8811121 Low B
18 -2.9659488 Low C
19 1.0506968 Low A
20 -1.0293305 Low B
21 -2.9776359 Low C
22 1.2007201 Low A
23 -0.8988021 Low B
24 -3.0302459 Low C
25 0.8974755 Low A
26 -1.0267385 Low B
27 -3.0199106 Low C
28 1.0131123 Low A
29 -0.9854200 Low B
30 -2.9637935 Low C
31 4.0673981 High A
32 3.2072036 High B
33 -1.2541029 High C
34 3.8929508 High A
35 2.9627543 High B
36 -1.2485141 High C
37 4.0274784 High A
38 2.9520487 High B
39 -1.1201895 High C
40 3.8995549 High A
41 3.0104984 High B
42 -1.3155993 High C
43 4.0578135 High A
44 2.8404374 High B
45 -1.2308504 High C
46 4.0449466 High A
47 2.9022947 High B
48 -1.1810002 High C
49 4.0731453 High A
50 2.9507401 High B
51 -1.2042685 High C
52 3.9887329 High A
53 3.0456827 High B
54 -0.9979665 High C
55 3.8949110 High A
56 3.0734652 High B
57 -1.1460750 High C
58 3.8685727 High A
59 2.9749961 High B
60 -1.1685795 High C
> mod2 <- lm(y~f1*f2)
> summary(mod2)
Call:
lm(formula = y ~ f1 * f2)
Residuals:
Min 1Q Median 3Q Max
-0.199479 -0.063752 -0.001089 0.058162 0.222229
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.97849 0.02865 34.15 <2e-16 ***
f1High 3.00306 0.04052 74.11 <2e-16 ***
f2B -1.97878 0.04052 -48.83 <2e-16 ***
f2C -4.00206 0.04052 -98.77 <2e-16 ***
f1High:f2B 0.98924 0.05731 17.26 <2e-16 ***
f1High:f2C -1.16620 0.05731 -20.35 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.09061 on 54 degrees of freedom
Multiple R-squared: 0.9988, Adjusted R-squared: 0.9987
F-statistic: 8785 on 5 and 54 DF, p-value: < 2.2e-16
- 온도: f1High, f1Low
- 질소: A, B, C (Low, Medium, High)
- 각각 Low가 control인 상태 (아웃풋에 High와 Medium, High)에 대한 정보가 출력)
이 때 coefficients를 이용해서 모델을 해석해보면
y hat ~ 0.97849 + 3.00306*f1High + -1.97878*f2B + -4.00206*f2C + 0.98924*f1High:f2B + -1.16620*f1High:f2C
| f2A | f2B | f2C | |
| f1Low | f1High = 0, f2B = 0, f2C = 0 y hat ~ 0.97849 + 3.00306*f1High + -1.97878*f2B + -4.00206*f2C + 0.98924*f1High:f2B + -1.16620*f1High:f2Cy hat ~ 0.97849 + 3.00306*(0) + -1.97878*(0) + -4.00206*(0) + 0.98924*(0):(0) + -1.16620*(0):(0)y hat ~ 0.97849 + | f1High = 0, f2A = 0, f2C = 0 y hat ~ 0.97849 + 3.00306*f1High + -1.97878*f2B + -4.00206*f2C + 0.98924*f1High:f2B + -1.16620*f1High:f2Cy hat ~ 0.97849 + 3.00306*(0) + -1.97878*(1) + -4.00206*(0) + 0.98924*(0):(1) + -1.16620*(0):(0)y hat ~ 0.97849 + -1.97878*(1) | f1High = 0, f2A = 0, f2B = 0 y hat ~ 0.97849 + 3.00306*f1High + -1.97878*f2B + -4.00206*f2C + 0.98924*f1High:f2B + -1.16620*f1High:f2Cy hat ~ 0.97849 + 3.00306*(0) + -1.97878*(0) + -4.00206*(1) + 0.98924*(0):(0) + -1.16620*(0):(1)y hat ~ 0.97849 + -4.00206*(1) |
| f1High | f1Low = 0, f1High = 1, f2B = 0, f2C = 0 y hat ~ 0.97849 + 3.00306*f1High + -1.97878*f2B + -4.00206*f2C + 0.98924*f1High:f2B + -1.16620*f1High:f2Cy hat ~ 0.97849 + 3.00306*(1) + -1.97878*(0) + -4.00206*(0) + 0.98924*(1):(0) + -1.16620*(1):(1)y hat ~ 0.97849 + 3.00306*(1) + -1.16620*(1):(1)y hat ~ 2.81535 | f1Low = 0, f1High = 1, f2A = 0, f2B = 1, f2C = 0 y hat ~ 0.97849 + 3.00306*f1High + -1.97878*f2B + -4.00206*f2C + 0.98924*f1High:f2B + -1.16620*f1High:f2Cy hat ~ 0.97849 + 3.00306*(1) + -1.97878*(1) + -4.00206*(0) + 0.98924*(1):(1) + -1.16620*(1):(0)y hat ~ 0.97849 + 3.00306*(1) + 0.98924*(1):(1)y hat ~ 4.97079 | f1Low = 0, f1High = 1, f2A = 0, f2B = 0, f2C = 1 y hat ~ 0.97849 + 3.00306*f1High + -1.97878*f2B + -4.00206*f2C + 0.98924*f1High:f2B + -1.16620*f1High:f2Cy hat ~ 0.97849 + 3.00306*(1) + -1.97878*(0) + -4.00206*(1) + 0.98924*(1):(0) + -1.16620*(1):(1)y hat ~ 0.97849 + 3.00306*(1) + -4.00206*(1) + -1.16620*(1):(1)y hat ~ -1.18671 |
| f2A | f2B | f2C | |
| f1Low | y hat ~ 0.97849 | y hat ~ -1.00029 | y hat -3.02357 |
| f1High | y hat ~ 2.81535 | y hat ~ 4.97079 | y hat ~ -1.18671 |
- 우선 f1High, f2B, f2C 가 나타나는 것은 f1Low, f2A가 default임을 의미 (즉, 온도가 낮고 질소함유량이 낮은 상태).
- (절편): 제어상태에서 (default = 둘다 Low = 온도가 낮고 질소가 낮은 상태) 식물의 줄기가 0.98cm 일 것임을 알 수 있다. 베이스라인으로 삼는다.
- f1High: 온도가 높고 질소가 낮은 상태에서 베이스라인에 비해서 3cm 크다.
- f2B:온도가 낮고 (제어상태) 질소가 Medium인 상태이면 베이스라인에 비해서 1.97cm 작다
- f2C: 온도가 낮고 (제어상태) 질소가 High인 상태이면 베이스라인에 비해서 4cm 작다
- f1High:f2B : 질소가 Medium이고 온도가 높은 상태이면, 질소가 미디엄이고 온도가 낮은 상태일 때보다 그 영향력이 1정도 증가한다. 즉, 질소 Medium: 온도High일 경우의 줄기의 길이는 -1.97 + 0.98 정도가 된다.
- f1High:f2C : 질소가 High이고 온도도 High인 상태 -1.16 감소한다.
> interact_plot(mod2, pred = "f1", modx = "f2")
> interact_plot(mod2, pred = "f2", modx = "f1")
Two continuous variables
# third case interaction between two continuous variables x1 <- runif(50, 0, 10) x2 <- rnorm(50, 10, 3) modmat <- model.matrix(~x1 * x2, data.frame(x1 = x1, x2 = x2)) coeff <- c(1, 2, -1, 1.5) y <- rnorm(50, mean = modmat %*% coeff, sd = 0.5) dat <- data.frame(y = y, x1 = x1, x2 = x2)
x1 = 온도
x2 = 질소응축량
y = bio mass (질량)
> dat
y x1 x2
1 127.225898 6.5782952 12.691470
2 134.976325 8.8407710 9.469827
3 172.978836 8.3999093 13.341127
4 129.187350 9.4216319 8.374333
5 95.970590 8.0393706 7.109805
6 113.477078 6.5829466 11.129345
7 66.270095 5.7813667 7.045979
8 126.863453 6.5519038 12.692678
9 131.624939 7.9795107 10.387788
10 110.456358 5.6903306 13.101109
11 115.479155 8.0144395 8.973132
12 29.528690 2.1448570 11.356844
13 128.318557 9.7465562 7.915786
14 18.921754 1.7368538 9.282959
15 -4.831214 0.1580690 6.978103
16 213.682344 8.8949841 15.780156
17 134.921126 8.3425580 10.154291
18 146.226900 6.4058502 15.401571
19 119.274576 8.7390817 8.345627
20 94.838213 5.9467854 10.321177
21 50.691137 2.9965236 12.367372
22 125.448494 8.4011628 9.267234
23 100.976142 5.9883009 11.152540
24 78.031250 7.1031208 6.492293
25 66.181384 3.3381367 14.554817
26 90.815310 5.8215147 10.218944
27 55.743255 4.2758748 8.416975
28 118.803590 8.6829426 8.426423
29 82.299096 4.5885828 12.240702
30 44.017352 4.2597642 6.452758
31 23.497249 2.6309321 5.935875
32 117.951117 7.9018964 9.363143
33 8.991443 1.0185476 9.731556
34 5.058066 0.8347121 10.771098
35 66.388066 3.5050761 13.612861
36 104.674052 6.9962838 9.477907
37 128.949834 6.9733668 12.070650
38 2.044139 0.6649924 11.240154
39 40.474643 4.2937384 5.708563
40 23.123469 2.5003389 6.100993
41 104.160548 5.0169870 14.210050
42 76.096597 5.2981234 9.341949
43 11.664929 1.0132115 16.397473
44 29.467472 3.6711480 4.499590
45 60.244671 4.1991523 9.668471
46 93.168095 5.1471371 12.297131
47 151.389142 8.7788236 10.970514
48 123.343902 9.5301753 7.793863
49 96.091697 4.9067381 13.437151
50 93.531181 6.4740823 9.165288
> summary(lm(y ~ x1 * x2))
Residuals:
Min 1Q Median 3Q Max
-0.68519 -0.19426 -0.03194 0.18262 0.71513
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.965921 0.284706 3.393 0.00143 **
x1 1.995115 0.049260 40.502 < 2e-16 ***
x2 -0.993288 0.027835 -35.685 < 2e-16 ***
x1:x2 1.499595 0.004651 322.443 < 2e-16 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3264 on 46 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 4.661e+05 on 3 and 46 DF, p-value: < 2.2e-16
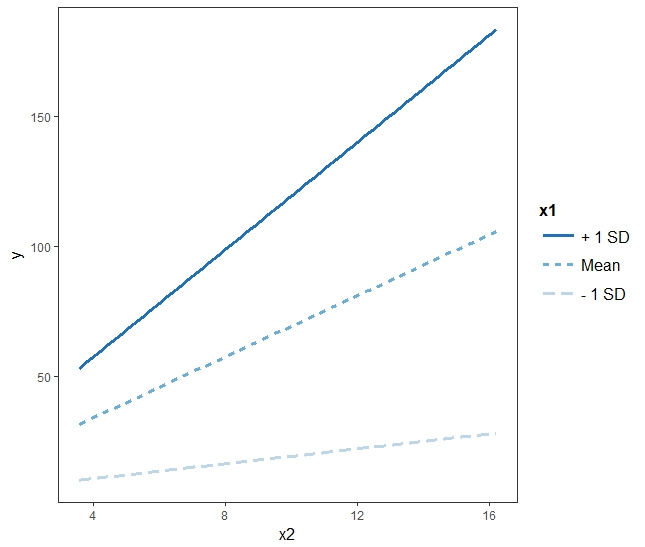
y hat ~ 0.965921 + 1.995115*x1 + -0.993288*x2 + 1.499595*x1*x2 y hat ~ 0.965921 + 1.995115*x1 + (-0.993288 + 1.499595*x1)*x2 y hat ~ 0.965921 + (1.995115 + 1.499595*x2)*x1 + -0.993288*x2
- (Intercept): at 0°C and with nitrogen concentration of 0 mg/g일때의 작물의 바이오매스량이 0.96 mg/g
- x1:
- nitrogen concentration of 0 mg/g인 상태에서
- 온도 x1이 1°C 증가할 때 마다
- 작물의 바이오매스량이 약 2 mg/g 증가
- x2:
- temperature of 0°C 상태에서
- x2인 nitrogen concentration 이 1 mg/g 증가할 때 마다
- 작물의 바이오매스량이 ~1 mg/g 정도씩 감소
- (위의 마지막 식에서) x1:x2 = x1*x2 : 질소량이 1씩 증가할 때 마다, 온도의 영향력은 1.5식 증가한다. 예를 들면 질소량이 0일 경우, 온도와 작물 간의 기울기는 약 2인데, 질소의 양이 1 증가하고 온도가 1 증가하면 기울기는 2 + 1.5 = 3.5가 된다.
# 0.97 = 1 로 보면 x2=1: 0.97 + *3.5 x1 + -1 (1=x2) 0 + 3.5 x1 x2=2: 0.97 + *5.0 x1 + -1 (2=x2) -1 + 5.0 x1 x2=3: 0.97 + *6.5 x1 + -1 (3=x2) -2 + 6.5 x1 x2=4: 0.97 + *8.0 x1 + -1 (4=x2) -3 + 8.0 x1 x2=5: 0.97 + *9.5 x1 + -1 (5=x2) -4 + 9.5 x1*(1.995115 + 1.499595*x2): x2=1: 3.495 ~ *3.5 x2=2: 4.994 ~ *5.0 x2=3: 6.494 ~ *6.5 x2=4: 7.994 ~ *8.0 x2=5: 9.493 ~ *9.5

yhat = 0.965921 + 1.995115*temp + -0.993288*nitro + 1.499595*inter
- 위의 그림에서 regression 라인 3개는 온도가 각각 0, 5, 10일 경우의 라인을 그린 것.
interact_plot(mod3, pred = "x2", modx = "x1")
E.g.2
# states.data <- readRDS("c:/Rstatistics/dataSets/states.rds")
states.data <- readRDS(url("http://commres.net/wiki/_media/r/states.rds"))
Or, read the above data file directly
z <- gzcon(url("http://commres.net/wiki/_media/r/states.rds"))
states.data <- readRDS(z)
head(states.data,5)
state region pop area density metro waste energy miles
1 Alabama South 4041000 52423 77.08 67.4 1.11 393 10.5
2 Alaska West 550000 570374 0.96 41.1 0.91 991 7.2
3 Arizona West 3665000 113642 32.25 79.0 0.79 258 9.7
4 Arkansas South 2351000 52075 45.15 40.1 0.85 330 8.9
5 California West 29760000 155973 190.80 95.7 1.51 246 8.7
toxic green house senate csat vsat msat percent expense income high
1 27.86 29.25 30 10 991 476 515 8 3627 27.498 66.9
2 37.41 NA 0 20 920 439 481 41 8330 48.254 86.6
3 19.65 18.37 13 33 932 442 490 26 4309 32.093 78.7
4 24.60 26.04 25 37 1005 482 523 6 3700 24.643 66.3
5 3.26 15.65 50 47 897 415 482 47 4491 41.716 76.2
college
1 15.7
2 23.0
3 20.3
4 13.3
5 23.4
> tail(states.data,5)
state region pop area density metro waste energy
47 Virginia South 6187000 39598 156.25 72.5 1.45 306
48 Washington West 4867000 66582 73.10 81.7 1.05 389
49 West Virginia South 1793000 24087 74.44 36.4 0.95 415
50 Wisconsin Midwest 4892000 54314 90.07 67.4 0.70 288
51 Wyoming West 454000 97105 4.68 29.6 0.70 786
miles toxic green house senate csat vsat msat percent expense
47 9.7 12.87 18.72 33 54 890 424 466 60 4836
48 9.2 8.51 16.51 52 64 913 433 480 49 5000
49 8.6 21.30 51.14 48 57 926 441 485 17 4911
50 9.1 9.20 20.58 47 57 1023 481 542 11 5871
51 12.8 25.51 114.40 0 10 980 466 514 13 5723
income high college
47 38.838 75.2 24.5
48 36.338 83.8 22.9
49 24.233 66.0 12.3
50 34.309 78.6 17.7
51 31.576 83.0 18.8
> data.info <- data.frame(attributes(states.data)[c("names", "var.labels")])
> # attributes(data) reveals various attributes of the data file,
> # which contains variable names and labels.
> data.info
names var.labels
1 state State
2 region Geographical region
3 pop 1990 population
4 area Land area, square miles
5 density People per square mile
6 metro Metropolitan area population, %
7 waste Per capita solid waste, tons
8 energy Per capita energy consumed, Btu
9 miles Per capita miles/year, 1,000
10 toxic Per capita toxics released, lbs
11 green Per capita greenhouse gas, tons
12 house House '91 environ. voting, %
13 senate Senate '91 environ. voting, %
14 csat Mean composite SAT score
15 vsat Mean verbal SAT score
16 msat Mean math SAT score
17 percent % HS graduates taking SAT
18 expense Per pupil expenditures prim&sec
19 income Median household income, $1,000
20 high % adults HS diploma
21 college % adults college degree
> str(states.data$region)
Factor w/ 4 levels "West","N. East",..: 3 1 1 3 1 1 2 3 NA 3 ...
# or
> attributes(data)["label.table"]
$label.table
$label.table$region
West N. East South Midwest
1 2 3 4
Simple regression
Political leaders may use mean SAT scores to make pointed comparisons between the educational systems of different US states. For example, some have raised the question of whether SAT scores are higher in states that spend more money on education. So, we regress per-pupil expenditures(expense) on SAT score (csat).
oneIV.model <- lm(csat ~ expense, data=states.data)
# 18 expense Per pupil expenditures prim&sec
summary(oneIV.model)
Call:
lm(formula = csat ~ expense, data = states.data)
Residuals:
Min 1Q Median 3Q Max
-131.811 -38.085 5.607 37.852 136.495
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.061e+03 3.270e+01 32.44 < 2e-16 ***
expense -2.228e-02 6.037e-03 -3.69 0.000563 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 59.81 on 49 degrees of freedom
Multiple R-squared: 0.2174, Adjusted R-squared: 0.2015
F-statistic: 13.61 on 1 and 49 DF, p-value: 0.0005631
As spending money on education, SAT scores gotten low? In other words, the more money a state spends on education, the lower its students' SAT scores. It is confirmed via:
- coefficient of expense: -2.228e-02 = -0.0228
- R2: 0.2174
- F (1,49) = 13.61 at p = 0.0005631
twoIV.model <- lm(csat ~ expense + percent, data = states.data)
# 18 expense Per pupil expenditures prim&sec
# 17 percent % HS graduates taking SAT
summary(twoIV.model)
Call:
lm(formula = csat ~ expense + percent, data = states.data)
Residuals:
Min 1Q Median 3Q Max
-62.921 -24.318 1.741 15.502 75.623
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 989.807403 18.395770 53.806 < 2e-16 ***
expense 0.008604 0.004204 2.046 0.0462 *
percent -2.537700 0.224912 -11.283 4.21e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 31.62 on 48 degrees of freedom
Multiple R-squared: 0.7857, Adjusted R-squared: 0.7768
F-statistic: 88.01 on 2 and 48 DF, p-value: < 2.2e-16
Then, what if we investigate an interaction effects of the two IVs?
twoIV.inta.model <- lm(csat ~ expense * percent, data = states.data)
summary(twoIV.inta.model)
Call:
lm(formula = csat ~ expense * percent, data = states.data)
Residuals:
Min 1Q Median 3Q Max
-65.359 -19.608 -3.046 17.528 76.176
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.048e+03 3.564e+01 29.415 < 2e-16 ***
expense -3.917e-03 7.756e-03 -0.505 0.6159
percent -3.809e+00 7.037e-01 -5.412 2.06e-06 ***
expense:percent 2.490e-04 1.310e-04 1.901 0.0635 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 30.8 on 47 degrees of freedom
Multiple R-squared: 0.801, Adjusted R-squared: 0.7883
F-statistic: 63.07 on 3 and 47 DF, p-value: < 2.2e-16
>
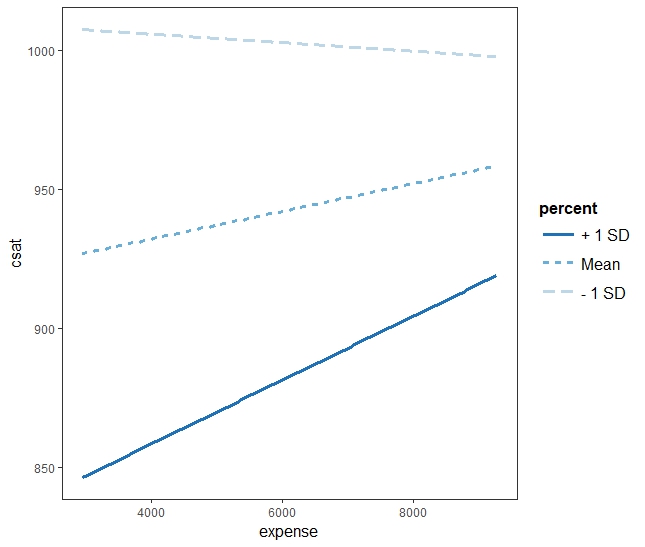
y hat = 1048 + -0.004 expense + -3.809 percent + 0.00025 expense:percent y hat = 1048 + -0.004 x1 + -3.809 x2 + 0.00025 x1x2 y hat = 1048 + (-0.004 + 0.00025 x2) x1 + -3.809 x2
> mm1 <- mean(states.data$percent) - sd(states.data$percent) > mp1 <- mean(states.data$percent) + sd(states.data$percent) > mp2 <- mean(states.data$percept) + (2*sd(states.data$percent) > mo0 <- mean(states.data$percent) > mm1 [1] 9.571891 > mp1 [1] 61.95752 > mp2 [1] 88.15033 > mo0 [1] 35.76471
> k <- c(mm1, mo0, mp1, mp2) > k [1] 9.571891 35.764706 61.957520 88.150335 > ic <- 1048 + (-3.809 * k) > ic [1] 1011.5407 911.7722 812.0038 712.2354 > x1.slope <- -0.004 + 0.00025 * k > x1.slope [1] -0.001607027 0.004941176 0.011489380 0.018037584 >
y hat when mm1 ~ 1011.5407 + -0.001607027 x1 y hat when mo0 ~ 911.7722 + 0.004941176 x1 y hat when mp1 ~ 812.0038 + 0.011489380 x1 y hat when mp2 ~ 712.2354 + 0.018037584 x1
- 위의 y hat은 (회귀식) 각각 percent 가 mean-1sd, mean, mean+1sd, 그리고 mean+2sd 일 경우의 식이 된다.
- x1 은 expense 이다.
- x2 는 10, 36, 62, 88% 의 응시율이다
- 10% 일 때는 expense가 한단위 증가할 때 마다 csat점수는 -0.0016의 기울기를 갖는다
- 36% 일 경우는 0.005 점 증가율을 갖는다
- 62 일 경우는 0.012 점 증가율을 갖는다
- 88 일 경우는 0.018 점 증가율을 갖는다
library(ggplot2)
library(jtools) # in case not loading, install.packages("jtools")
library(interactions) # interact_plot requires this package now
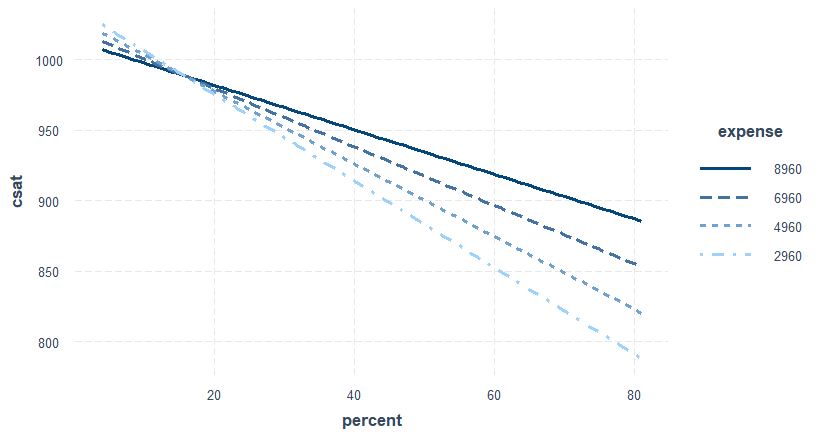
interact_plot(twoIV.inta.model, pred = "expense", modx = "percent") interact_plot(twoIV.model, pred = "expense", modx = "percent")
Analysis again
attach(states.data)
n.1 <- lm(csat~expense)
n.2 <- lm(csat~percent)
n.12 <- lm(csat~expense+percent)
n.12i <- lm(csat~expense*percent)
n.1i <- lm(csat~expense+expense:percent)
n.2i <- lm(csat~percent+expense:percent)
n.2i.temp <- lm(csat~percent+percent:expense)
n.i <- lm(csat~expense:percent)
s.n.1 <- summary(n.1)
s.n.2 <- summary(n.2)
s.n.12 <- summary(n.12)
s.n.12i <- summary(n.12i)
s.n.1i <- summary(n.1i)
s.n.2i <- summary(n.2i)
s.n.2i.temp <- summary(n.2i.temp)
s.n.i <- summary(n.i)
s.n.12i
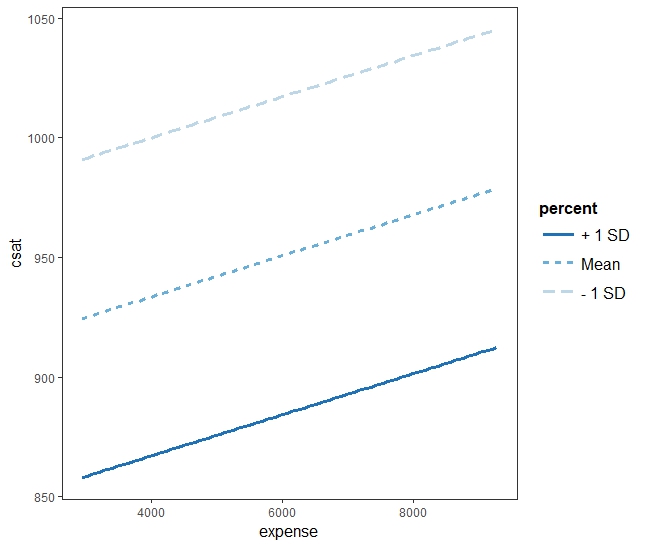
# y hat ~ 1048 + -0.003917 x1 + -3.809 x2 + 0.000249 x1 x2
# y hat ~ 1048 + -0.003917 x1 + (-3.809 + 0.000249 x1) x2
# x2를 (percent를) 중심으로 보기
e.mm1 <- mean(expense)-sd(expense)
e.m0 <- mean(expense)
e.mp1 <- mean(expense)+sd(expense)
e.mp2 <- mean(expense)+(2*sd(expense))
# x1의 case가 4가지 (holding constants)
k <- c(e.mm1, e.m0, e.mp1, e.mp2)
ic <- 1048 + (-0.003917*k)
slp <- -3.809 + (0.000249*k)
ic
slp
# y hat ~ 1032.979 - 2.85 x2
# y hat ~ 1027.491 - 2.51 x2
# y hat ~ 1022.002 - 2.16 x2
# y hat ~ 1016.514 - 1.81 x2
interact_plot(n.12i,
pred = "percent",
modx = "expense",
modx.values = k)
# or
mne <- min(expense)
mxe <- max(expense)
kk <- seq(mne, mxe, by = 2000)
interact_plot(n.12i,
pred = "percent",
modx = "expense",
modx.values = kk)
> n.1 <- lm(csat~expense)
> n.2 <- lm(csat~percent)
> n.12 <- lm(csat~expense+percent)
> n.12i <- lm(csat~expense*percent)
> n.1i <- lm(csat~expense+expense:percent)
> n.2i <- lm(csat~percent+expense:percent)
> n.2i.temp <- lm(csat~percent+percent:expense)
> n.i <- lm(csat~expense:percent)
>
> s.n.1 <- summary(n.1)
> s.n.2 <- summary(n.2)
> s.n.12 <- summary(n.12)
> s.n.12i <- summary(n.12i)
> s.n.1i <- summary(n.1i)
> s.n.2i <- summary(n.2i)
> s.n.2i.temp <- summary(n.2i.temp)
> s.n.i <- summary(n.i)
>
> s.n.12i
Call:
lm(formula = csat ~ expense * percent)
Residuals:
Min 1Q Median 3Q Max
-65.36 -19.61 -3.05 17.53 76.18
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.05e+03 3.56e+01 29.41 < 2e-16 ***
expense -3.92e-03 7.76e-03 -0.51 0.616
percent -3.81e+00 7.04e-01 -5.41 2.1e-06 ***
expense:percent 2.49e-04 1.31e-04 1.90 0.063 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 30.8 on 47 degrees of freedom
Multiple R-squared: 0.801, Adjusted R-squared: 0.788
F-statistic: 63.1 on 3 and 47 DF, p-value: <2e-16
>
> # y hat ~ 1048 + -0.003917 x1 + -3.809 x2 + 0.000249 x1 x2
> # y hat ~ 1048 + -0.003917 x1 + (-3.809 + 0.000249 x1) x2
> # x2를 (percent를) 중심으로 보기
>
> e.mm1 <- mean(expense)-sd(expense)
> e.m0 <- mean(expense)
> e.mp1 <- mean(expense)+sd(expense)
> e.mp2 <- mean(expense)+(2*sd(expense))
>
> # x1의 case가 4가지 (holding constants)
> k <- c(e.mm1, e.m0, e.mp1, e.mp2)
> ic <- 1048 + (-0.003917*k)
> slp <- -3.809 + (0.000249*k)
> ic
[1] 1033 1027 1022 1017
> slp
[1] -2.854 -2.505 -2.156 -1.807
>
> # y hat ~ 1032.979 - 2.85 x2
> # y hat ~ 1027.491 - 2.51 x2
> # y hat ~ 1022.002 - 2.16 x2
> # y hat ~ 1016.514 - 1.81 x2
>
> interact_plot(n.12i,
+ pred = "percent",
+ modx = "expense",
+ modx.values = k)
> # or
> mne <- min(expense)
> mxe <- max(expense)
> kk <- seq(mne, mxe, by = 2000)
> interact_plot(n.12i,
+ pred = "percent",
+ modx = "expense",
+ modx.values = kk)
>
아래 그림에서처럼 대학지원 퍼센티지가 높아지면 성적이 떨어지는 경향을 보이는데, 이 경향은 해당 주가 얼마나 sat교육에 돈을 투자하는가에 따라서 달라진다. 많이 투자하는 경우에는 지원율이 높아도 떨어지는 비율이 지원율이 낮은 경우보다 현저히 낮다.
언제 interaction effect를 분석에 넣는가?
interaction effects가 significant할 때에 넣는다
significant하지 않을 때에는 additive model을 (+사인 모델) 사용한다.
One categorical IV
> attributes(data)["label.table"]
$label.table
$label.table$region
West N. East South Midwest
1 2 3 4
> sat.region <- lm(csat ~ region, data=states.data)
> summary(sat.region)
Call:
lm(formula = csat ~ region, data = states.data)
Residuals:
Min 1Q Median 3Q Max
-145.083 -29.389 -3.778 35.192 85.000
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 946.31 14.80 63.958 < 2e-16 ***
regionN. East -56.75 23.13 -2.453 0.01800 *
regionSouth -16.31 19.92 -0.819 0.41719
regionMidwest 63.78 21.36 2.986 0.00451 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 53.35 on 46 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.3853, Adjusted R-squared: 0.3452
F-statistic: 9.61 on 3 and 46 DF, p-value: 4.859e-05
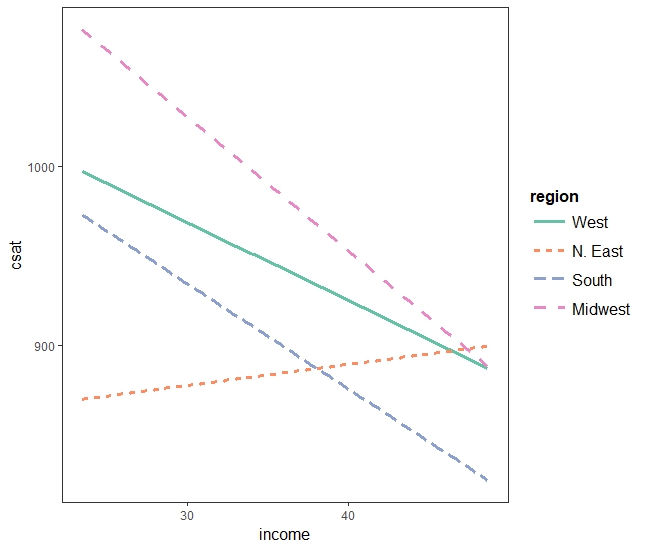
regionWest: 946.31 + 0 = 946.31 regionN. East: 946.31 - 56.75 = 889.56 regionSouth: 946.31 - 16.31 = 930 regionMidwest: 946.31 + 63.78 = 1010.09
One numerical and one categorical IV
> sat.ri <- lm(csat ~ income * region, data=states.data)
> #Show the results
> summary(sat.ri)
Call:
lm(formula = csat ~ income * region, data = states.data)
Residuals:
Min 1Q Median 3Q Max
-135.962 -20.479 -0.973 28.308 81.188
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1099.843 74.252 14.812 <2e-16 ***
income -4.369 2.080 -2.100 0.0418 *
regionN. East -257.071 134.989 -1.904 0.0637 .
regionSouth 11.062 95.176 0.116 0.9080
regionMidwest 151.386 148.286 1.021 0.3131
income:regionN. East 5.543 3.489 1.588 0.1197
income:regionSouth -1.509 2.815 -0.536 0.5947
income:regionMidwest -3.089 4.462 -0.692 0.4926
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 46.8 on 42 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.568, Adjusted R-squared: 0.4959
F-statistic: 7.887 on 7 and 42 DF, p-value: 4.366e-06
>
interact_plot(sat.ri, pred = "income", modx = "region")
E.g. 3
data: state.x77 in r
?state.x77 attributes(state.x77) > attributes(state.x77) $dim [1] 50 8 $dimnames $dimnames[[1]] [1] "Alabama" "Alaska" "Arizona" [4] "Arkansas" "California" "Colorado" [7] "Connecticut" "Delaware" "Florida" [10] "Georgia" "Hawaii" "Idaho" [13] "Illinois" "Indiana" "Iowa" [16] "Kansas" "Kentucky" "Louisiana" [19] "Maine" "Maryland" "Massachusetts" [22] "Michigan" "Minnesota" "Mississippi" [25] "Missouri" "Montana" "Nebraska" [28] "Nevada" "New Hampshire" "New Jersey" [31] "New Mexico" "New York" "North Carolina" [34] "North Dakota" "Ohio" "Oklahoma" [37] "Oregon" "Pennsylvania" "Rhode Island" [40] "South Carolina" "South Dakota" "Tennessee" [43] "Texas" "Utah" "Vermont" [46] "Virginia" "Washington" "West Virginia" [49] "Wisconsin" "Wyoming" $dimnames[[2]] [1] "Population" "Income" "Illiteracy" "Life Exp" [5] "Murder" "HS Grad" "Frost" "Area"
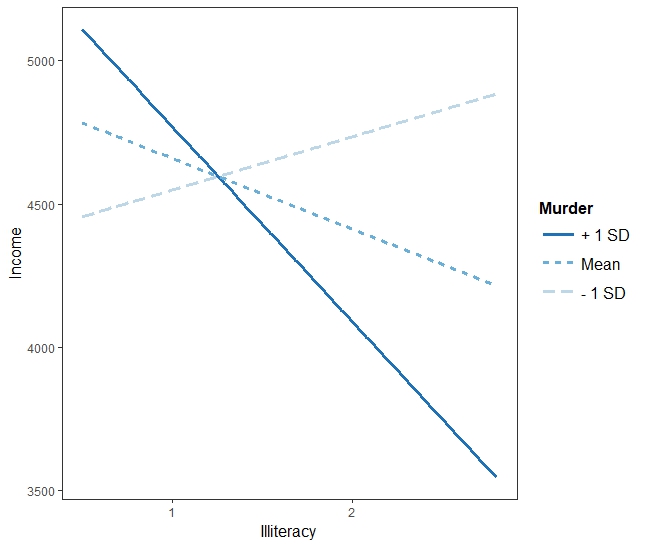
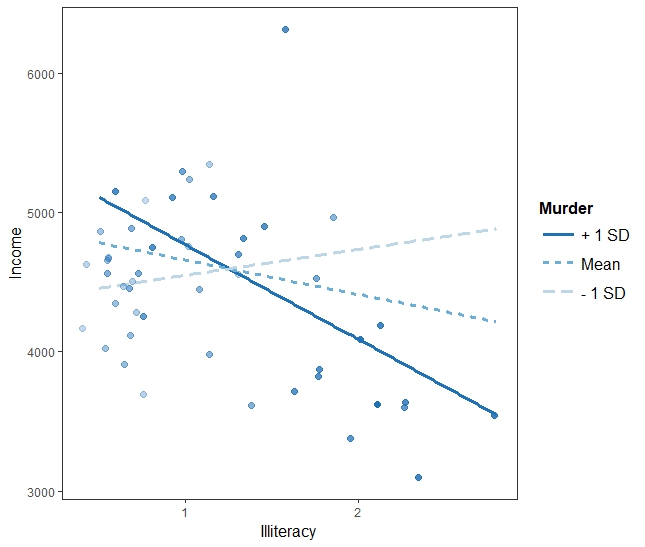
아래의 경우 interaction effect는 중요한 의미를 갖는다. additive model에서는 murder가 중요한 역할을 하지 않지만, interactive model에서는 Illiteracy와 결합하여 중요한 역할을 하는 것으로 해석될 수 있다.
fit <- lm(Income ~ Illiteracy + Murder, data = as.data.frame(state.x77)) fiti <- lm(Income ~ Illiteracy * Murder, data = as.data.frame(state.x77)) summary(fit) summary(fiti)
> fit <- lm(Income ~ Illiteracy + Murder, data = as.data.frame(state.x77))
> fiti <- lm(Income ~ Illiteracy * Murder, data = as.data.frame(state.x77))
> summary(fit)
Call:
lm(formula = Income ~ Illiteracy + Murder, data = as.data.frame(state.x77))
Residuals:
Min 1Q Median 3Q Max
-880.9 -397.3 -51.3 333.1 1960.7
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4890.5 187.6 26.06 <2e-16 ***
Illiteracy -548.7 184.6 -2.97 0.0046 **
Murder 25.4 30.5 0.83 0.4089
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 560 on 47 degrees of freedom
Multiple R-squared: 0.203, Adjusted R-squared: 0.169
F-statistic: 5.98 on 2 and 47 DF, p-value: 0.00486
> summary(fiti)
Call:
lm(formula = Income ~ Illiteracy * Murder, data = as.data.frame(state.x77))
Residuals:
Min 1Q Median 3Q Max
-955.2 -326.0 10.7 300.0 1892.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3822.6 405.3 9.43 2.5e-12 ***
Illiteracy 617.3 434.9 1.42 0.1624
Murder 146.8 50.3 2.92 0.0054 **
Illiteracy:Murder -117.1 40.1 -2.92 0.0054 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 520 on 46 degrees of freedom
Multiple R-squared: 0.327, Adjusted R-squared: 0.283
F-statistic: 7.46 on 3 and 46 DF, p-value: 0.000359
>
> interact_plot(fiti, pred = "Illiteracy", modx = "Murder")
interact_plot(fiti, pred = "Illiteracy", modx = "Murder", plot.points = TRUE)
Eg. 4
# Load the data
data("marketing", package = "datarium")
set.seed(123)
training.samples <- marketing$sales %>%
createDataPartition(p = 0.8, list = FALSE)
train.data <- marketing[training.samples, ]
test.data <- marketing[-training.samples, ]
model2 <- lm(sales ~ youtube + facebook + youtube:facebook,
data = marketing)
# Or simply, use this:
model2 <- lm(sales ~ youtube*facebook, data = train.data)
# Summarize the model
summary(model2)
interact_plot(model2, pred="youtube", modx="facebook")
Ex.
Use Cars93 dataset.
What is affecting city mileage?
1. EngineSize
2. EngineSize * Origin
3. EngineSize + Length
4. EngineSize * Length
Print out the summaries of each lm + interaction graph.
Interprete what has been found.
Ex. 3
library(foreign)
library(msm)
d <- read.dta("https://stats.idre.ucla.edu/stat/data/hsbdemo.dta")
attach(d)
attributes(d)
summary(cbind(read, math, socst))
- Do a regression test on read score with math
- Do a regression test on read with socst
- What do the two test tell you?
- Now,
- Do a regression test on read score with math and socst (interaction effects considered or included).
- How do you interpret the result.
- Draw a plot to make your interpretation easy to understand