multicollinearity
Table of Contents
Multicollinearity and Singularity
변인들 간의 상관관계가 극한 정도로 이루어질 때 multicollinearity가 있다고 한다. 예를 들어 IQ score와 수학점수는 상당한 상관관계에 있을 것이다. 이 두 변인은 서로 비숫한 대상(현상)을 측정한 것이기 때문이다. 이 두 변인이 독립변인으로 regression과 같은 test에 사용된다면, 동일한 현상에 대한 설명력을 나눠가지려고 하기때문에 문제를 일으키게 된다.
만약에 IQ점수와 IQ점수의 세부점수들을 (지각력, 공간력, 수학력, 언어능력이라고 가정하면) 간의 관계는 사실 동일한 것이라고 하겠다. IQ점수는 이 세부점수를 모두 더한 값이기 때문이다. 이와 같은 상황을 Singularity라고 한다.
see Singularity
Testing multicollinearity with correlation matrix
options(digits = 4)
HSGPA <- c(3.0, 3.2, 2.8, 2.5, 3.2, 3.8, 3.9, 3.8, 3.5, 3.1)
FGPA <- c(2.8, 3.0, 2.8, 2.2, 3.3, 3.3, 3.5, 3.7, 3.4, 2.9)
SATV <- c(500, 550, 450, 400, 600, 650, 700, 550, 650, 550)
scholar <- data.frame(FGPA, HSGPA, SATV) # collect into a data frame
# install.packages("psych")
# library(psych)
describe(scholar) # provides descrptive information about each variable
corrs <- cor(scholar) # find the correlations and set them into an object called 'corrs'
corrs # print corrs
pairs(scholar) # pairwise scatterplots
attach(scholar)
# install.packages("corrplot")
library(corrplot)
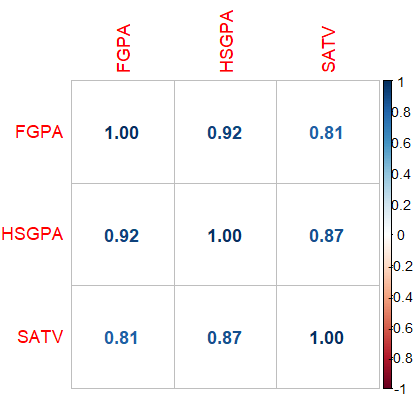
corrplot(cor(scholar), method = "number")
독립변인인 SATV와 HSGPA 간의 상관관계가 상당히 높다는 것을 알 수 있다 (r = 0.87).
using Tolerance
m.tolerance <- lm(SATV~HSGPA, data=scholar) summary(m.tolerance) 1 - summary(m.tolerance)$r.squared # 0.1보다 작으면 가능성이 아주 많음 # 위의 이야기는 자신을 제외한 다른 독립변인들과의 상관관계가 0.9 이상이면 문제라는 이야기
> m.tolerance <- lm(SATV~HSGPA, data=scholar)
> summary(m.tolerance)
Call:
lm(formula = SATV ~ HSGPA, data = scholar)
Residuals:
Min 1Q Median 3Q Max
-101.86 -19.29 1.14 28.31 54.13
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -19.4 114.6 -0.17 0.86967
HSGPA 176.7 34.6 5.10 0.00093 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 48.2 on 8 degrees of freedom
Multiple R-squared: 0.765, Adjusted R-squared: 0.735
F-statistic: 26 on 1 and 8 DF, p-value: 0.00093
> tol <- 1 - summary(m.tolerance)$r.squared
> tol
[1] 0.2352
using VIF (Variance Inflation Factors)
Variance Inflation Factor 는 독립변인의 계수값에 인플레이션이 있는지 확인해 보는 방법으로 VIF = 1 인 경우, 해당 독립변인이 다른 변인들에 의해 영향을 받지 않았다는 것을 의미한다. 아래처럼 구한다. 일반적으로 VIF 값이 5 이상이면 주목하여 살펴본다. 10 이상이면 multicollinearity를 의미한다고 한다.
tol <- 1- summary(m.tolerance)$r.squared tol m.vif <- 1/tol m.vif
> tol <- 1- summary(m.tolerance)$r.squared > tol [1] 0.2352 > m.vif <- 1/tol > m.vif [1] 4.251 >
R 에서는
m.a <- lm(FGPA ~ SATV+HSGPA, data = scholar)
summary(m.a)
# install.packages("olsrr")
# library(olsrr)
ols_vif_tol(m.a)
> m.a <- lm(FGPA ~ SATV+HSGPA, data = scholar)
> summary(m.a)
Call:
lm(formula = FGPA ~ SATV + HSGPA, data = scholar)
Residuals:
Min 1Q Median 3Q Max
-0.2431 -0.1125 -0.0286 0.1269 0.2716
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.233102 0.456379 0.51 0.625
SATV 0.000151 0.001405 0.11 0.917
HSGPA 0.845192 0.283816 2.98 0.021 *
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.192 on 7 degrees of freedom
Multiple R-squared: 0.851, Adjusted R-squared: 0.809
F-statistic: 20.1 on 2 and 7 DF, p-value: 0.00126
> # install.packages("olsrr")
> # library(olsrr)
> ols_vif_tol(m.a)
Variables Tolerance VIF
1 SATV 0.2352 4.251
2 HSGPA 0.2352 4.251
>
using condition index
ols_eigen_cindex(m.a)
> ols_eigen_cindex(m.a) Eigenvalue Condition Index intercept SATV HSGPA 1 2.983908 1.00 0.001961 0.0006461 0.0004659 2 0.013568 14.83 0.837019 0.1204555 0.0222304 3 0.002524 34.38 0.161020 0.8788984 0.9773037 >
multicollinearity.txt · Last modified: by hkimscil