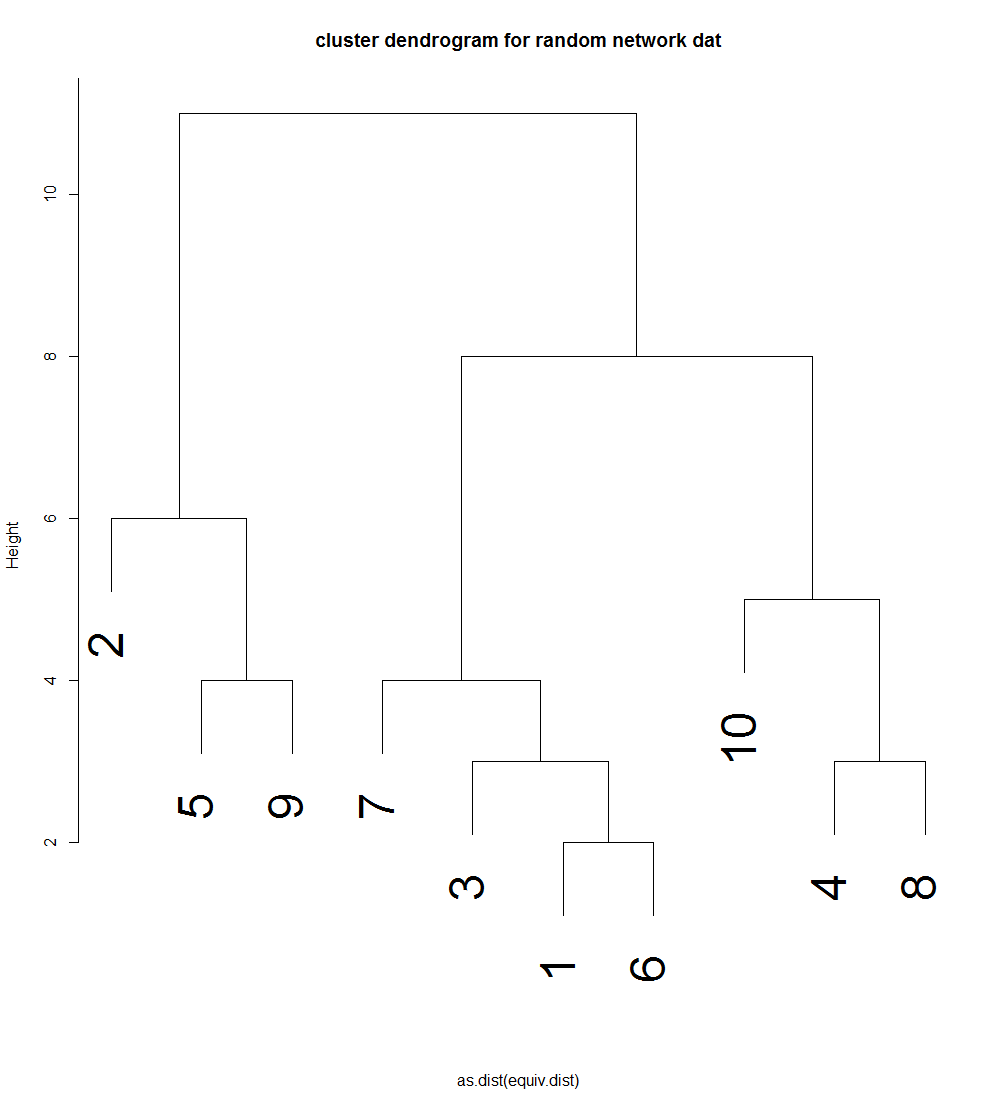network_groups
Identifying groups of networks
setwd(“D:/Users/Hyo/Cs-Kant/CS/Classes/sna_examples/sna_in_r”)
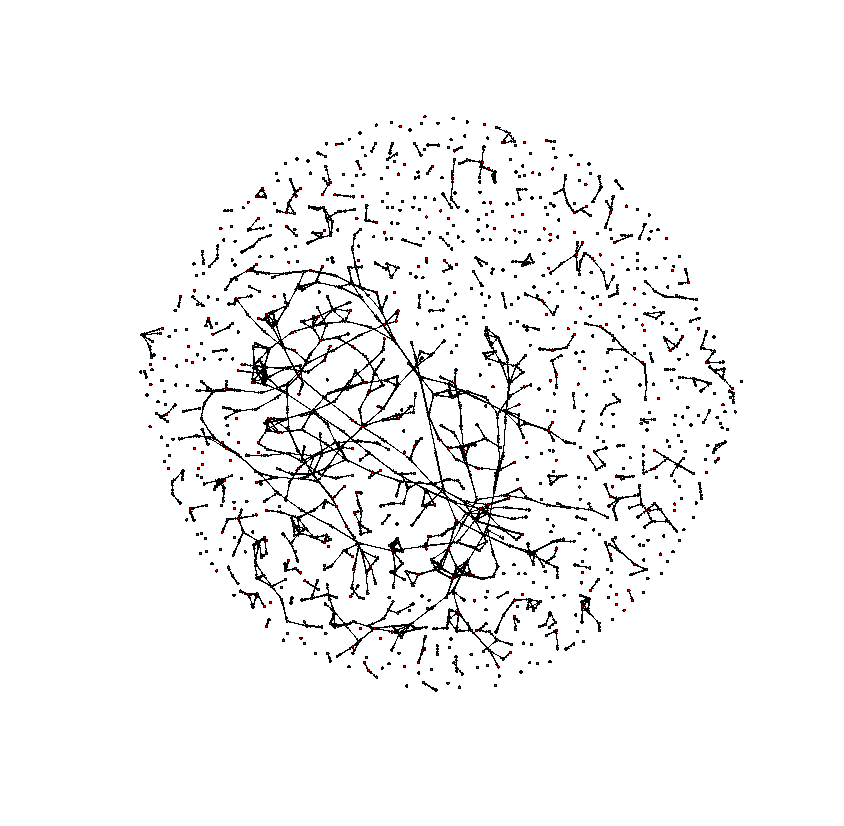
# Network's characteristics and subgroups library(sna) # Faux Magnolia High School data library(ergm) data(faux.magnolia.high) summary(faux.magnolia.high) fmh <- as.sociomatrix(faux.magnolia.high) gplot(fmh, vertex.cex=0.5, arrowhead.cex=0.5)
round(gden(fmh),4)
[1] 9e-04 = 0.00091
transivity
fmh2 <- fmh %*% fmh (denom <- sum(fmh2)-sum(diag(fmh2))) (num <- sum(fmh2 * fmh)) round(num/denom,3) round(gtrans(fmh),3)
> fmh2 <- fmh %*% fmh > (denom <- sum(fmh2)-sum(diag(fmh2))) [1] 3642 > (num <- sum(fmh2 * fmh)) [1] 1014 > round(num/denom,3) [1] 0.278 > round(gtrans(fmh),3) [1] 0.278
reciprocity
# knoke.infor network is given in Chapter 2, Section 1
library(sna)
knoke.infor <- as.matrix(read.table("knoke-infor.txt",header=T))
rownames(knoke.infor) <- colnames(knoke.infor)
(num <- sum(knoke.infor * t(knoke.infor)))
(denom <- sum(knoke.infor))
round(num/denom,3)
round(grecip(knoke.infor, measure="edgewise"),3)
# knoke.money network
knoke.money <- as.matrix(read.table("knoke-money.txt",header=T))
rownames(knoke.money) <- colnames(knoke.money)
# dyad and triad patterns in knoke-infor and knoke-money
dyad.census(knoke.infor)
dyad.census(knoke.money)
triad.census(knoke.infor)
triad.census(knoke.money)
> dyad.census(knoke.infor)
Mut Asym Null
[1,] 17 15 13
> dyad.census(knoke.money)
Mut Asym Null
[1,] 1 20 24
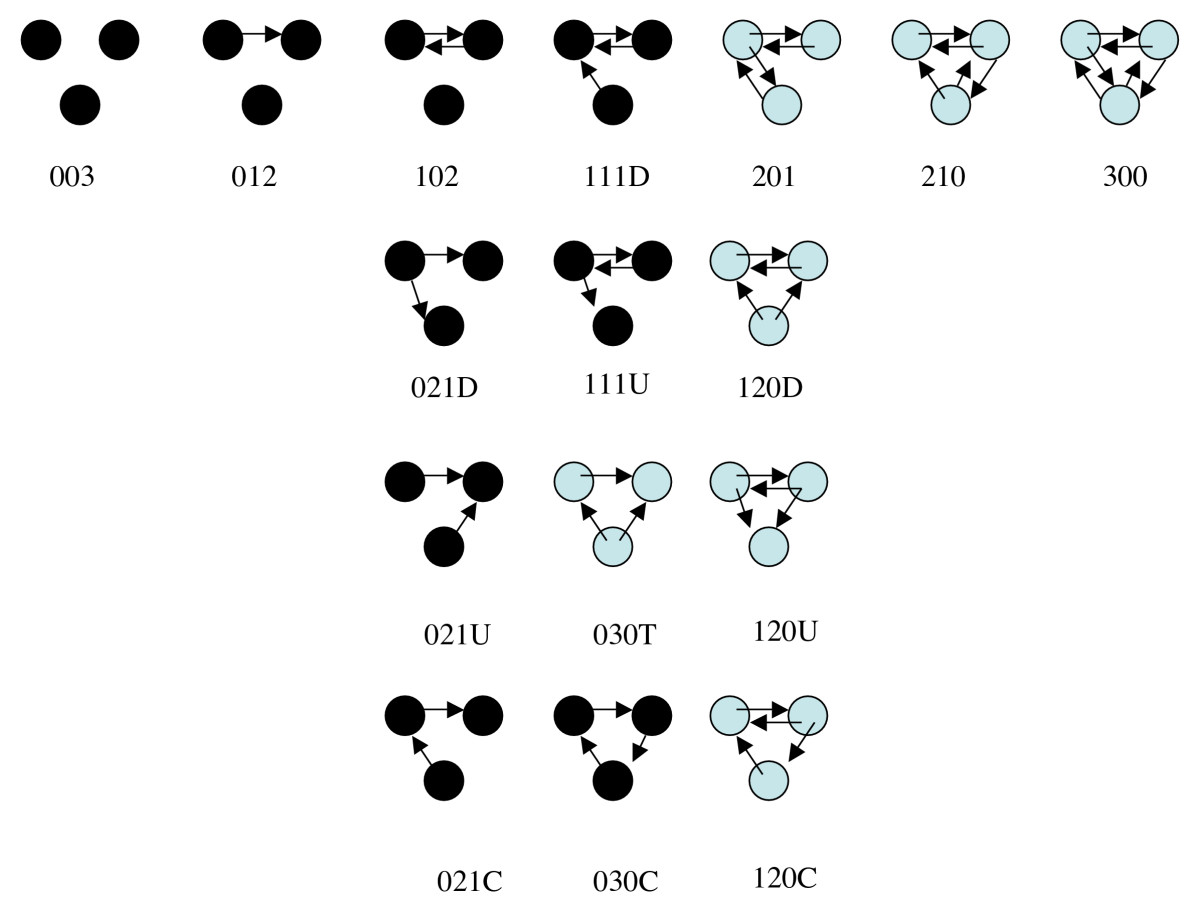
> triad.census(knoke.infor)
003 012 102 021D 021U 021C 111D 111U 030T 030C 201 120D 120U 120C 210 300
[1,] 3 13 12 1 13 3 10 4 7 0 14 4 2 1 24 9
> triad.census(knoke.money)
003 012 102 021D 021U 021C 111D 111U 030T 030C 201 120D 120U 120C 210 300
[1,] 20 48 2 10 13 7 1 1 14 0 0 3 0 1 0 0
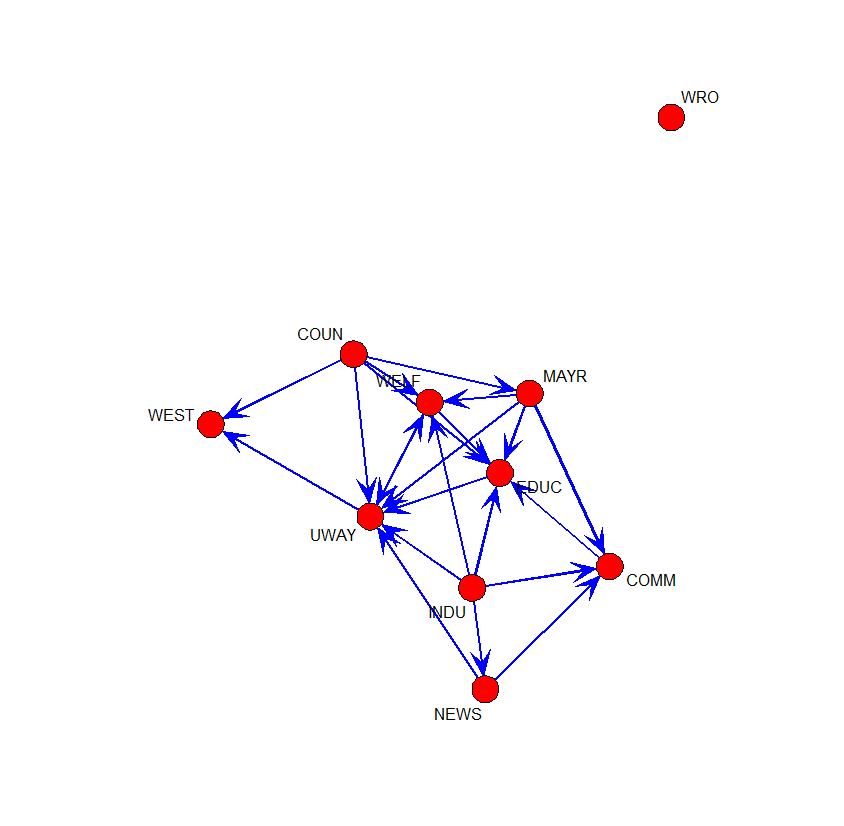
component.dist(knoke.money)
- COUN: county government
- COMM: chamber of commerce
- EDUC: board of education
- INDU: Industry development agency
- MAYR: Mayor
- WRO: Women Right Organization group
- NEWS: Newspaper
- WAY: United Way (private organization)
- WELF: Welfare
- WEST: West group (private organization)
> component.dist(knoke.money) $membership [1] 1 2 3 4 5 6 7 3 3 8 $csize [1] 1 1 3 1 1 1 1 1 $cdist [1] 7 0 1 0 0 0 0 0 0 0
Identifying sub-group
library(sna) # Faux Magnolia High School data (Continued) library(ergm) data(faux.magnolia.high) summary(faux.magnolia.high) fmh<-as.sociomatrix(faux.magnolia.high) gplot(fmh, vertex.cex=.5, arrowhead.cex=.3) round(gden(fmh),4) round(gtrans(fmh),3) components(fmh) fmh.comp = component.dist(fmh) table(fmh.comp$csize) head(fmh.comp$membership,100) grp2 <- (1:1461)[fmh.comp$membership=="2"] str(grp2)
> round(gden(fmh),4)
[1] 9e-04
> round(gtrans(fmh),3)
[1] 0.278
Warning message:
In gtrans(fmh) :
gtrans called with use.adjacency=TRUE, but your data looks
too large for that to work well.
Overriding to edgelist method.
> components(fmh)
[1] 661
> fmh.comp = component.dist(fmh)
> table(fmh.comp$csize)
1 2 3 4 5 6 7 8 9 11 12 19 23 439
524 64 29 11 12 4 7 4 1 1 1 1 1 1
> head(fmh.comp$membership,100)
[1] 1 2 2 2 2 3 2 4 5 6 7 8 9 2 10 2 11 12 11 13 2 14 15 16 2 17 18 19 20 21
[31] 22 23 24 25 26 27 2 2 28 29 2 30 31 32 33 34 2 35 36 2 37 38 2 39 40 41 42 43 44 45
[61] 2 46 2 47 2 48 49 11 2 38 8 2 2 50 51 52 53 11 54 55 56 11 2 57 58 2 59 60 22 11
[91] 61 2 62 63 64 65 22 66 67 68
> grp2 <- (1:1461)[fmh.comp$membership=="2"]
> str(grp2)
int [1:439] 2 3 4 5 7 14 16 21 25 37 ...
>
fmh.clique <- clique.census(fmh, clique.comembership="bysize") names(fmh.clique) str(fmh.clique$cliques) core.list <- c(122,183,530,1143,1160) # fmh.clique$cliques[[5]] fmh.comp$membership[core.list] fmh[core.list,core.list] summary(sort(geodist(fmh)$gdist[122,])[2:439])[-4] # end
> fmh.clique <- clique.census(fmh, clique.comembership="bysize")
> names(fmh.clique)
[1] "clique.count" "clique.comemb" "cliques"
> str(fmh.clique$cliques)
List of 5
$ :List of 524
..$ : int 1457
..$ : int 1456
..$ : int 1455
..$ : int 1451
..$ : int 1449
..$ : int 1448
..$ : int 1443
..$ : int 1440
..$ : int 1438
..$ : int 1437
..$ : int 1436
..$ : int 1435
..$ : int 1431
..$ : int 1427
..$ : int 1426
..$ : int 1425
..$ : int 1421
..$ : int 1418
..$ : int 1416
..$ : int 1413
..$ : int 1412
..$ : int 1410
..$ : int 1408
..$ : int 1407
..$ : int 1403
..$ : int 1402
..$ : int 1399
..$ : int 1394
..$ : int 1393
..$ : int 1387
..$ : int 1386
..$ : int 1384
..$ : int 1380
..$ : int 1379
..$ : int 1374
..$ : int 1373
..$ : int 1371
..$ : int 1367
..$ : int 1364
..$ : int 1362
..$ : int 1359
..$ : int 1351
..$ : int 1350
..$ : int 1347
..$ : int 1343
..$ : int 1334
..$ : int 1329
..$ : int 1327
..$ : int 1326
..$ : int 1325
..$ : int 1321
..$ : int 1320
..$ : int 1319
..$ : int 1318
..$ : int 1315
..$ : int 1314
..$ : int 1311
..$ : int 1310
..$ : int 1307
..$ : int 1306
..$ : int 1305
..$ : int 1304
..$ : int 1303
..$ : int 1301
..$ : int 1297
..$ : int 1296
..$ : int 1294
..$ : int 1289
..$ : int 1286
..$ : int 1278
..$ : int 1276
..$ : int 1275
..$ : int 1273
..$ : int 1268
..$ : int 1259
..$ : int 1257
..$ : int 1253
..$ : int 1249
..$ : int 1247
..$ : int 1245
..$ : int 1241
..$ : int 1236
..$ : int 1235
..$ : int 1234
..$ : int 1233
..$ : int 1229
..$ : int 1225
..$ : int 1224
..$ : int 1223
..$ : int 1219
..$ : int 1218
..$ : int 1216
..$ : int 1214
..$ : int 1213
..$ : int 1211
..$ : int 1207
..$ : int 1200
..$ : int 1199
..$ : int 1198
.. [list output truncated]
$ :List of 626
..$ : int [1:2] 1299 1424
..$ : int [1:2] 1279 1382
..$ : int [1:2] 1265 1417
..$ : int [1:2] 1254 1258
..$ : int [1:2] 1147 1239
..$ : int [1:2] 1130 1372
..$ : int [1:2] 1119 1452
..$ : int [1:2] 1203 1452
..$ : int [1:2] 1102 1138
..$ : int [1:2] 1102 1119
..$ : int [1:2] 1002 1292
..$ : int [1:2] 930 1398
..$ : int [1:2] 917 930
..$ : int [1:2] 977 1406
..$ : int [1:2] 977 1011
..$ : int [1:2] 898 1011
..$ : int [1:2] 884 975
..$ : int [1:2] 909 1108
..$ : int [1:2] 865 1108
..$ : int [1:2] 841 958
..$ : int [1:2] 838 1461
..$ : int [1:2] 1196 1357
..$ : int [1:2] 770 1332
..$ : int [1:2] 748 911
..$ : int [1:2] 737 1036
..$ : int [1:2] 713 1352
..$ : int [1:2] 785 821
..$ : int [1:2] 711 821
..$ : int [1:2] 666 867
..$ : int [1:2] 664 679
..$ : int [1:2] 643 759
..$ : int [1:2] 616 695
..$ : int [1:2] 608 1390
..$ : int [1:2] 608 1013
..$ : int [1:2] 602 1141
..$ : int [1:2] 591 966
..$ : int [1:2] 587 644
..$ : int [1:2] 579 654
..$ : int [1:2] 576 1290
..$ : int [1:2] 556 561
..$ : int [1:2] 555 844
..$ : int [1:2] 551 964
..$ : int [1:2] 537 992
..$ : int [1:2] 534 1238
..$ : int [1:2] 534 988
..$ : int [1:2] 1252 1256
..$ : int [1:2] 529 1422
..$ : int [1:2] 520 848
..$ : int [1:2] 519 546
..$ : int [1:2] 514 1037
..$ : int [1:2] 504 1283
..$ : int [1:2] 500 984
..$ : int [1:2] 949 1244
..$ : int [1:2] 652 1244
..$ : int [1:2] 856 1447
..$ : int [1:2] 633 1244
..$ : int [1:2] 633 944
..$ : int [1:2] 633 856
..$ : int [1:2] 508 1244
..$ : int [1:2] 496 1447
..$ : int [1:2] 628 1058
..$ : int [1:2] 486 637
..$ : int [1:2] 486 628
..$ : int [1:2] 627 1168
..$ : int [1:2] 455 1128
..$ : int [1:2] 440 1007
..$ : int [1:2] 440 583
..$ : int [1:2] 430 1331
..$ : int [1:2] 430 864
..$ : int [1:2] 429 710
..$ : int [1:2] 417 1340
..$ : int [1:2] 1055 1146
..$ : int [1:2] 407 1055
..$ : int [1:2] 1059 1444
..$ : int [1:2] 639 1146
..$ : int [1:2] 639 1059
..$ : int [1:2] 407 1038
..$ : int [1:2] 445 1227
..$ : int [1:2] 445 918
..$ : int [1:2] 404 445
..$ : int [1:2] 403 580
..$ : int [1:2] 399 1328
..$ : int [1:2] 1277 1453
..$ : int [1:2] 1337 1453
..$ : int [1:2] 1269 1337
..$ : int [1:2] 387 1453
..$ : int [1:2] 386 1348
..$ : int [1:2] 617 1182
..$ : int [1:2] 370 1182
..$ : int [1:2] 1189 1454
..$ : int [1:2] 1189 1428
..$ : int [1:2] 995 1428
..$ : int [1:2] 995 1285
..$ : int [1:2] 369 1189
..$ : int [1:2] 368 459
..$ : int [1:2] 366 1139
..$ : int [1:2] 796 839
..$ : int [1:2] 362 839
..$ : int [1:2] 1004 1181
.. [list output truncated]
$ :List of 106
..$ : int [1:3] 809 1196 1360
..$ : int [1:3] 666 1115 1355
..$ : int [1:3] 666 1112 1355
..$ : int [1:3] 664 1266 1370
..$ : int [1:3] 531 888 1252
..$ : int [1:3] 478 593 627
..$ : int [1:3] 478 494 593
..$ : int [1:3] 768 1007 1376
..$ : int [1:3] 573 678 1333
..$ : int [1:3] 541 553 1445
..$ : int [1:3] 541 553 1423
..$ : int [1:3] 161 653 1172
..$ : int [1:3] 109 336 1232
..$ : int [1:3] 94 108 1293
..$ : int [1:3] 978 1201 1430
..$ : int [1:3] 93 588 1430
..$ : int [1:3] 686 721 804
..$ : int [1:3] 275 797 1177
..$ : int [1:3] 142 804 899
..$ : int [1:3] 64 686 721
..$ : int [1:3] 1071 1085 1369
..$ : int [1:3] 59 1176 1375
..$ : int [1:3] 916 928 1039
..$ : int [1:3] 31 97 377
..$ : int [1:3] 78 375 876
..$ : int [1:3] 78 283 876
..$ : int [1:3] 19 68 419
..$ : int [1:3] 19 68 375
..$ : int [1:3] 680 859 1383
..$ : int [1:3] 680 859 1378
..$ : int [1:3] 859 1069 1302
..$ : int [1:3] 680 859 1069
..$ : int [1:3] 263 1000 1378
..$ : int [1:3] 263 615 1000
..$ : int [1:3] 996 1217 1404
..$ : int [1:3] 940 962 1188
..$ : int [1:3] 919 1009 1316
..$ : int [1:3] 786 788 906
..$ : int [1:3] 584 1095 1322
..$ : int [1:3] 568 1053 1054
..$ : int [1:3] 568 718 1053
..$ : int [1:3] 550 749 991
..$ : int [1:3] 550 650 749
..$ : int [1:3] 552 562 752
..$ : int [1:3] 517 1204 1255
..$ : int [1:3] 501 744 1345
..$ : int [1:3] 490 630 1057
..$ : int [1:3] 483 765 1150
..$ : int [1:3] 480 512 764
..$ : int [1:3] 471 745 857
..$ : int [1:3] 471 632 857
..$ : int [1:3] 769 1129 1391
..$ : int [1:3] 449 769 1391
..$ : int [1:3] 395 589 743
..$ : int [1:3] 347 1312 1429
..$ : int [1:3] 299 323 603
..$ : int [1:3] 299 323 408
..$ : int [1:3] 374 396 861
..$ : int [1:3] 279 374 780
..$ : int [1:3] 396 692 861
..$ : int [1:3] 279 374 396
..$ : int [1:3] 278 409 1175
..$ : int [1:3] 274 1381 1389
..$ : int [1:3] 325 1110 1450
..$ : int [1:3] 325 833 1450
..$ : int [1:3] 227 439 1459
..$ : int [1:3] 216 1312 1429
..$ : int [1:3] 487 650 749
..$ : int [1:3] 487 630 991
..$ : int [1:3] 410 1356 1420
..$ : int [1:3] 172 410 1356
..$ : int [1:3] 528 558 1056
..$ : int [1:3] 528 558 980
..$ : int [1:3] 528 558 622
..$ : int [1:3] 170 528 558
..$ : int [1:3] 846 942 1152
..$ : int [1:3] 727 846 1152
..$ : int [1:3] 158 906 1019
..$ : int [1:3] 779 1019 1226
..$ : int [1:3] 158 779 1019
..$ : int [1:3] 141 817 941
..$ : int [1:3] 133 1178 1281
..$ : int [1:3] 157 195 1178
..$ : int [1:3] 157 195 926
..$ : int [1:3] 133 157 1178
..$ : int [1:3] 128 1354 1365
..$ : int [1:3] 122 183 1414
..$ : int [1:3] 122 722 1143
..$ : int [1:3] 183 559 1414
..$ : int [1:3] 150 1153 1261
..$ : int [1:3] 150 356 1061
..$ : int [1:3] 92 766 1349
..$ : int [1:3] 92 1121 1349
..$ : int [1:3] 92 1121 1267
..$ : int [1:3] 92 766 1267
..$ : int [1:3] 264 1284 1342
..$ : int [1:3] 72 301 1458
..$ : int [1:3] 72 301 784
..$ : int [1:3] 72 264 1284
.. [list output truncated]
$ :List of 15
..$ : int [1:4] 240 767 1300 1401
..$ : int [1:4] 535 646 765 947
..$ : int [1:4] 535 646 724 765
..$ : int [1:4] 290 836 1187 1335
..$ : int [1:4] 251 688 1087 1419
..$ : int [1:4] 487 729 749 991
..$ : int [1:4] 487 492 729 991
..$ : int [1:4] 122 1143 1160 1415
..$ : int [1:4] 285 425 590 817
..$ : int [1:4] 121 296 677 794
..$ : int [1:4] 121 291 296 677
..$ : int [1:4] 114 890 1061 1261
..$ : int [1:4] 114 150 1061 1261
..$ : int [1:4] 425 590 817 941
..$ : int [1:4] 83 425 590 817
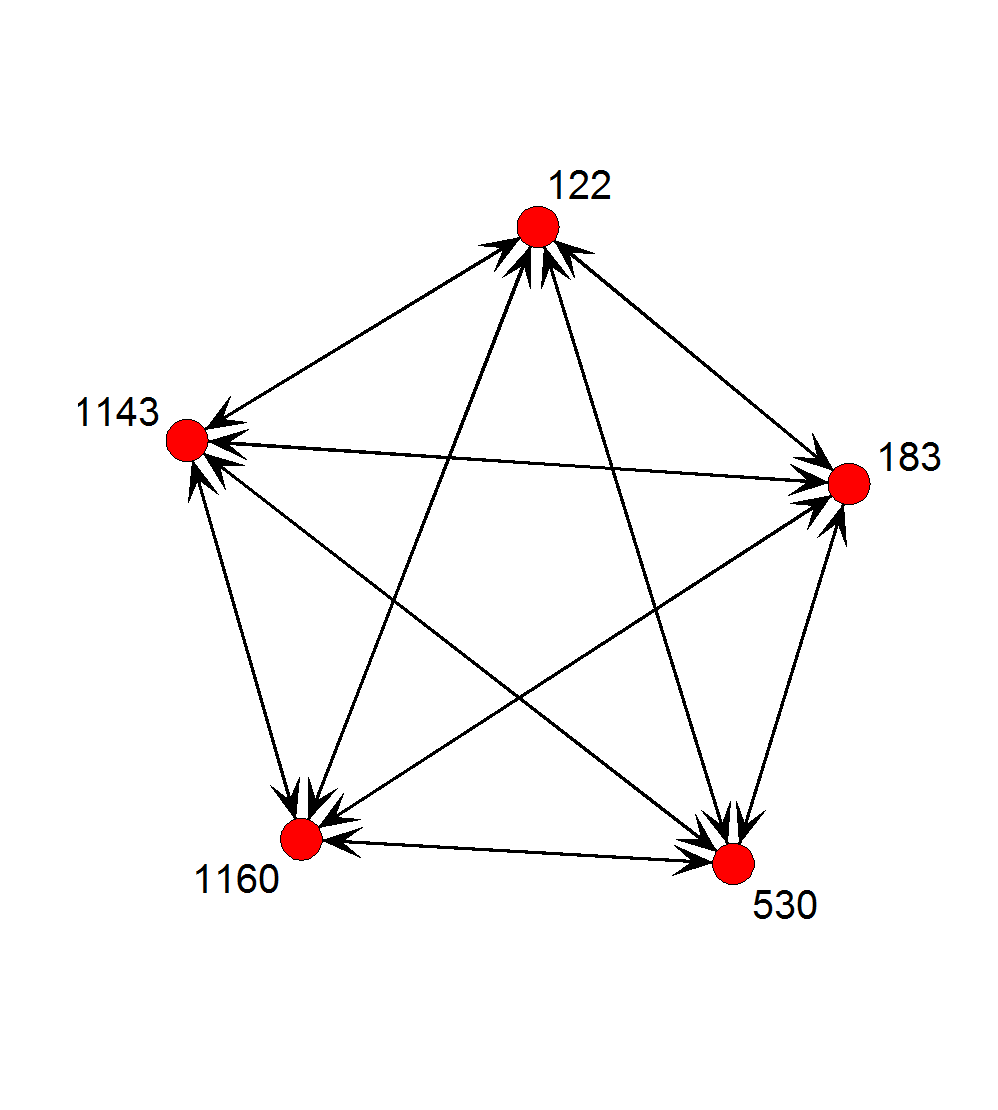
$ :List of 1
..$ : int [1:5] 122 183 530 1143 1160
> core.list <- c(122,183,530,1143,1160) # fmh.clique$cliques[[5]]
> fmh.comp$membership[core.list]
[1] 2 2 2 2 2
> fmh[core.list,core.list]
122 183 530 1143 1160
122 0 1 1 1 1
183 1 0 1 1 1
530 1 1 0 1 1
1143 1 1 1 0 1
1160 1 1 1 1 0
> summary(sort(geodist(fmh)$gdist[122,])[2:439])[-4]
Min. 1st Qu. Median 3rd Qu. Max.
1 11 14 17 25
>
위의 str(fmh.clique$cliques) 는
fmh.clique 라는 데이터를
clique.census(fmh, . . . .)를 이용하여 생성하고
거기서 발견되는 클리크(cliques)들을 나열해 본것.
아웃풋은 하나로 이루어진 클리크는 524개
둘로 이루어진 클리크는 626개
셋으로 이루어진 클리크는 106개
넷으로 이루어진 클리크는 15개
그리고 다섯으로 이루어진 클리크는 1개가 있다는 것 (list of 1)
그 멤버들은 122, 183, 530, 1143, 1160 이다.
Clique 정의에 따라서 이들은 maximal complete link (모두 연결되어 있는) 관계의 집단이다.
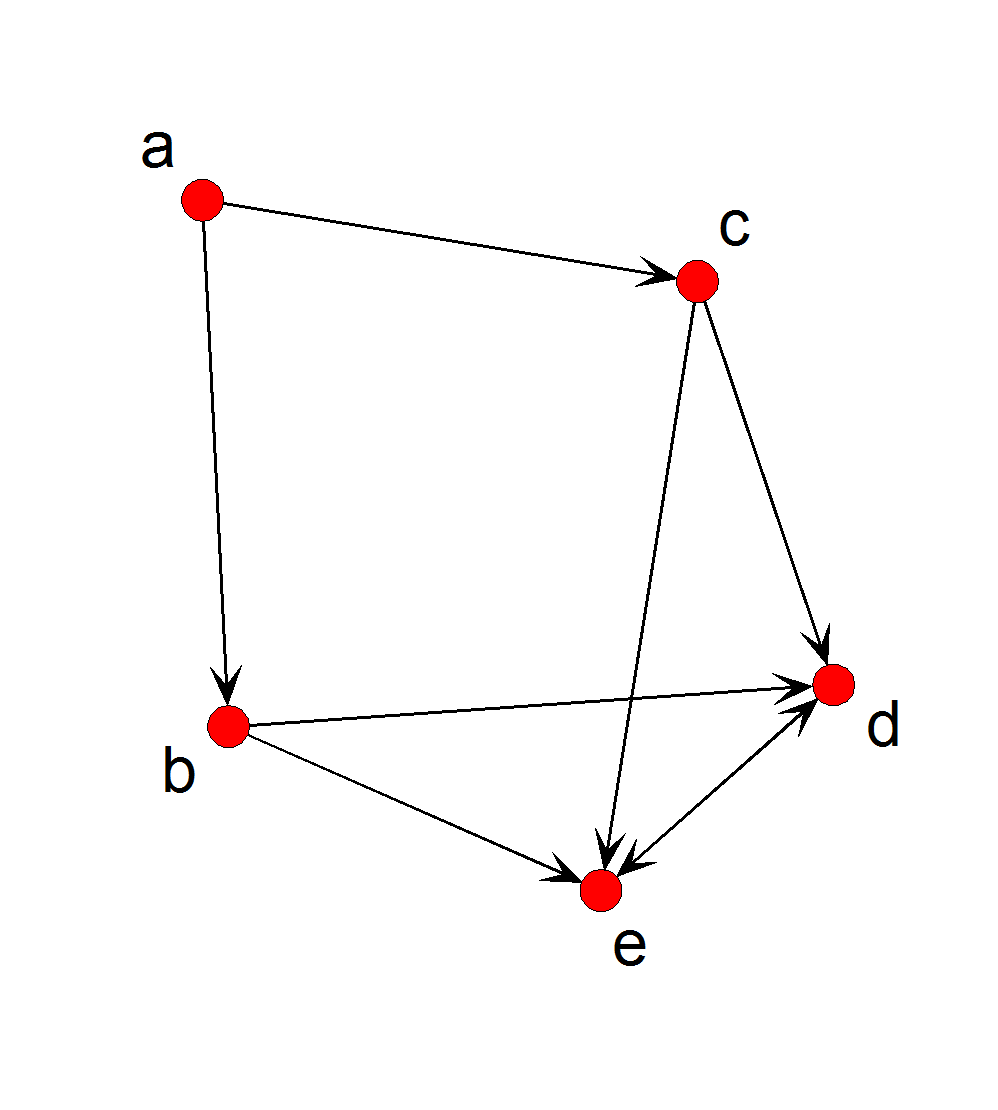
s = matrix(0,5,5)
edge.list = matrix ( c(1,2, 1,3, 2,4, 2,5, 3,4, 3,5, 4,5, 5,4), byrow=T, ncol=2)
s[edge.list]=1
s
rownames(s)<-c("a", "b", "c", "d", "e")
colnames(s)<-c("a", "b", "c", "d", "e")
> s
> s = matrix(0,5,5)
> edge.list = matrix ( c(1,2, 1,3, 2,4, 2,5, 3,4, 3,5, 4,5, 5,4), byrow=T, ncol=2)
> s[edge.list] = 1
> s
[,1] [,2] [,3] [,4] [,5]
[1,] 0 1 1 0 0
[2,] 0 0 0 1 1
[3,] 0 0 0 1 1
[4,] 0 0 0 0 1
[5,] 0 0 0 1 0
눈으로 봐서 a를 중심으로 좌우동형이므로 b, c와 d,e는 각각 등치 (등가)라고 할 수 있다. 이를 수식으로 구하기 위한 접근 방법으로는 연결을 1, 비연결을 0으로 한 각 노드(점) 간의 거리를 구하여 거리가 가까운 것들을 모아 놓으면 될 것이다. 가장 흔한 예가 Hamming distance:
- see P02mJhS9qQ4
예:
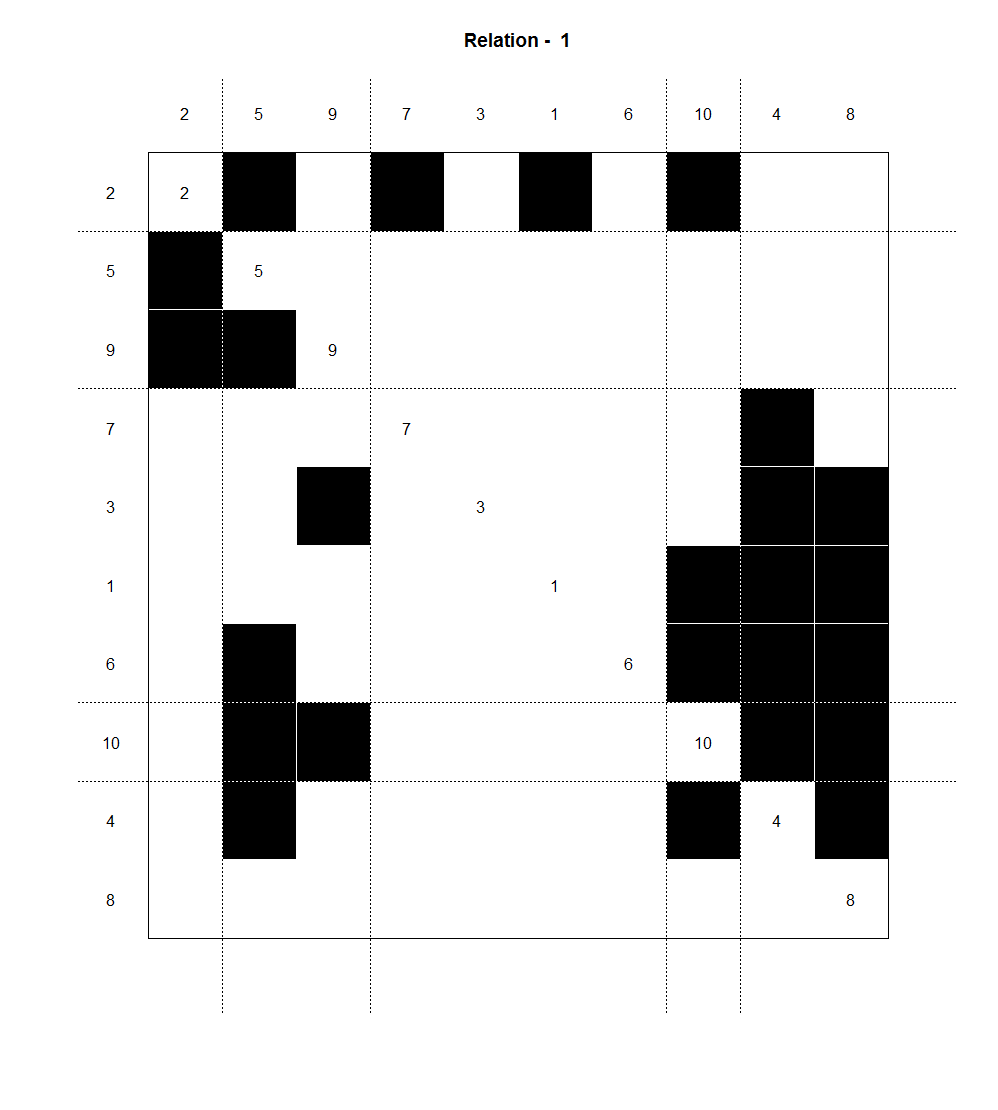
library(sna) set.seed(123) p1<-runif(10,0,1) p2<-runif(10,0,1) G1<-rgraph(10,tprob=sapply(p1,rep,10)) G2<-rgraph(10,tprob=t(sapply(p2,rep,10))) G<-G1*G2 G hamming.G=sedist(G,method="hamming") cluster <- equiv.clust(G, method="hamming", cluster.method="complete") b.mdoel <- blockmodel(G, cluster, h=4.5) b.model plot(b.model)
> b.mdoel <- blockmodel(G, cluster, h=4.5)
> b.model
Network Blockmodel:
Block membership:
1 2 3 4 5 6 7 8 9 10
1 2 1 3 4 1 1 3 4 5
Reduced form blockmodel:
Block 1 Block 2 Block 3 Block 4 Block 5
Block 1 0.0 0 0.875 0.25 0.5
Block 2 0.5 NaN 0.000 0.50 1.0
Block 3 0.0 0 0.500 0.25 0.5
Block 4 0.0 1 0.000 0.50 0.0
Block 5 0.0 0 1.000 1.00 NaN
> plot(b.model)
network_groups.txt · Last modified: by hkimscil