partial_and_semipartial_correlation
Table of Contents
Partial and semi-partial correlation
references
The Elements of Statistical Learning or local copy
or Introduction to R for Data Science :: Session 7 (Multiple Linear Regression Model in R + Categorical Predictors, Partial and Part Correlation)
Partial and semipartial
options(digits = 4) HSGPA <- c(3.0, 3.2, 2.8, 2.5, 3.2, 3.8, 3.9, 3.8, 3.5, 3.1) FGPA <- c(2.8, 3.0, 2.8, 2.2, 3.3, 3.3, 3.5, 3.7, 3.4, 2.9) SATV <- c(500, 550, 450, 400, 600, 650, 700, 550, 650, 550) scholar <- data.frame(FGPA, HSGPA, SATV) # collect into a data frame describe(scholar) # provides descrptive information about each variable corrs <- cor(scholar) # find the correlations and set them into an object called 'corrs' corrs # print corrs pairs(scholar) # pairwise scatterplots
attach(scholar) # freshman's gpa ~ hischool gpa + sat mod.all <- lm(FGPA ~ HSGPA+ SATV, data = scholar) summary(mod.all)
> mod.all <- lm(FGPA ~ HSGPA+ SATV, data = scholar)
> summary(mod.all)
Call:
lm(formula = FGPA ~ HSGPA + SATV, data = scholar)
Residuals:
Min 1Q Median 3Q Max
-0.2431 -0.1125 -0.0286 0.1269 0.2716
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.233102 0.456379 0.51 0.625
HSGPA 0.845192 0.283816 2.98 0.021 *
SATV 0.000151 0.001405 0.11 0.917
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.192 on 7 degrees of freedom
Multiple R-squared: 0.851, Adjusted R-squared: 0.809
F-statistic: 20.1 on 2 and 7 DF, p-value: 0.00126
>
>
SATV 는 significant한 역할을 하지 못한다는 t-test 결과이다. 이것이 사실일까?
우선 FGPA에 대해 SATV와 HSGPA를 가지고 regression을 각각 해보자
아래의 결과는 두개의 IV는 각각 종속변인인 FGPA를 significant하게 설명하고 있다.
즉, 둘이 같이 설명하려고 했을 때에만 그 설명력이 사라진다.
attach(scholar) ma1 <- lm(FGPA ~ SATV) ma2 <- lm(FGPA ~ HSGPA) summary(ma1) summary(ma2)
> ma1 <- lm(FGPA ~ SATV)
> ma2 <- lm(FGPA ~ HSGPA)
> summary(ma1)
Call:
lm(formula = FGPA ~ SATV)
Residuals:
Min 1Q Median 3Q Max
-0.2804 -0.1305 -0.0566 0.0350 0.6481
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.95633 0.54419 1.76 0.1169
SATV 0.00381 0.00096 3.97 0.0041 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.27 on 8 degrees of freedom
Multiple R-squared: 0.663, Adjusted R-squared: 0.621
F-statistic: 15.8 on 1 and 8 DF, p-value: 0.00412
> summary(ma2)
Call:
lm(formula = FGPA ~ HSGPA)
Residuals:
Min 1Q Median 3Q Max
-0.2434 -0.1094 -0.0266 0.1259 0.2797
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.230 0.426 0.54 0.60412
HSGPA 0.872 0.129 6.77 0.00014 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.179 on 8 degrees of freedom
Multiple R-squared: 0.851, Adjusted R-squared: 0.833
F-statistic: 45.8 on 1 and 8 DF, p-value: 0.000143
>
아래는 HSGPA의 영향력을 IV, DV 모두에게서 제거한 후, DV에 대한 IV의 영향력을 보는 작업이다.
m1 <- lm(FGPA ~ HSGPA) m2 <- lm(SATV ~ HSGPA) res.m1 <- resid(m1) # res.m1 <- m1$residuals res.m2 <- resid(m2) m.12 <- lm(res.m1 ~ res.m2) summary(m.12)
결과는 아래에서 보는 것처럼 not significant하다.
> m1 <- lm(FGPA ~ HSGPA)
> m2 <- lm(SATV ~ HSGPA)
> res.m1 <- resid(m1)
> res.m2 <- resid(m2)
> m.12 <- lm(res.m1 ~ res.m2)
> summary(m.12)
Call:
lm(formula = res.m1 ~ res.m2)
Residuals:
Min 1Q Median 3Q Max
-0.2431 -0.1125 -0.0286 0.1269 0.2716
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.50e-18 5.67e-02 0.00 1.00
res.m2 1.51e-04 1.31e-03 0.12 0.91
Residual standard error: 0.179 on 8 degrees of freedom
Multiple R-squared: 0.00165, Adjusted R-squared: -0.123
F-statistic: 0.0132 on 1 and 8 DF, p-value: 0.911
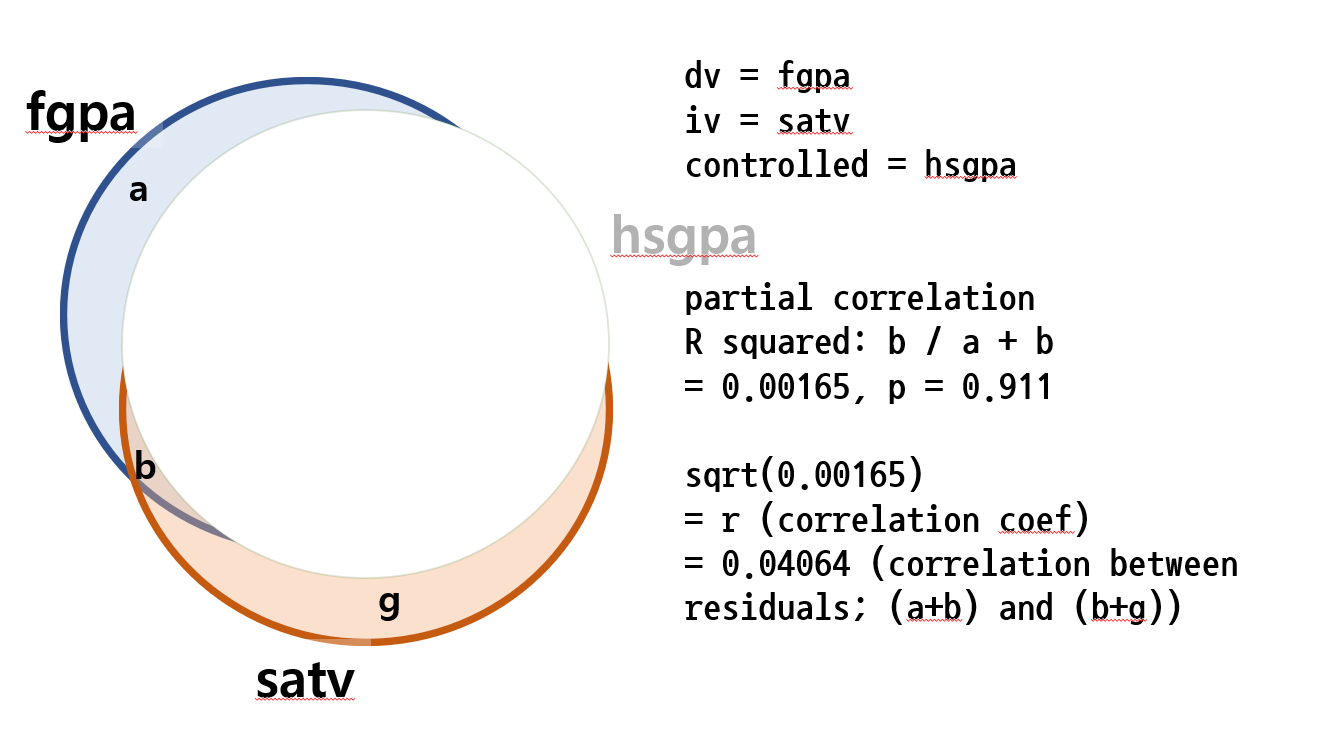
특히 위에서 R-squared value는 0.00165이고 이를 square root 한 값은 $\sqrt{0.00165} = 0.04064$ 이다. 이 값은 HSGPA의 영향력을 IV와 (SATV) DV에서 (FGPA) 모두 제거한 후의 correlation값이라고도 할 수 있다. 사실 이 숫자는 lm()말고도
cor(res.m1, res.m2) ## 혹은 cor.test(res.m1, res.m2)
으로 확인해 볼 수 있다.
> cor(res.m1, res.m2)
[1] 0.04064
>
> cor.test(res.m1, res.m2)
Pearson's product-moment correlation
data: res.m1 and res.m2
t = 0.12, df = 8, p-value = 0.9
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.6045 0.6535
sample estimates:
cor
0.04064
>
우리는 이것을 partial correlation이라고 부른다는 것을 알고 있다. 이를 ppcor 패키지를 이용해서 테스트해보면
# install.packages("ppcor")
pcor.test(FGPA, SATV, HSGPA)
> pcor.test(FGPA, SATV, HSGPA) estimate p.value statistic n gp Method 1 0.04064 0.9173 0.1076 10 1 pearson >
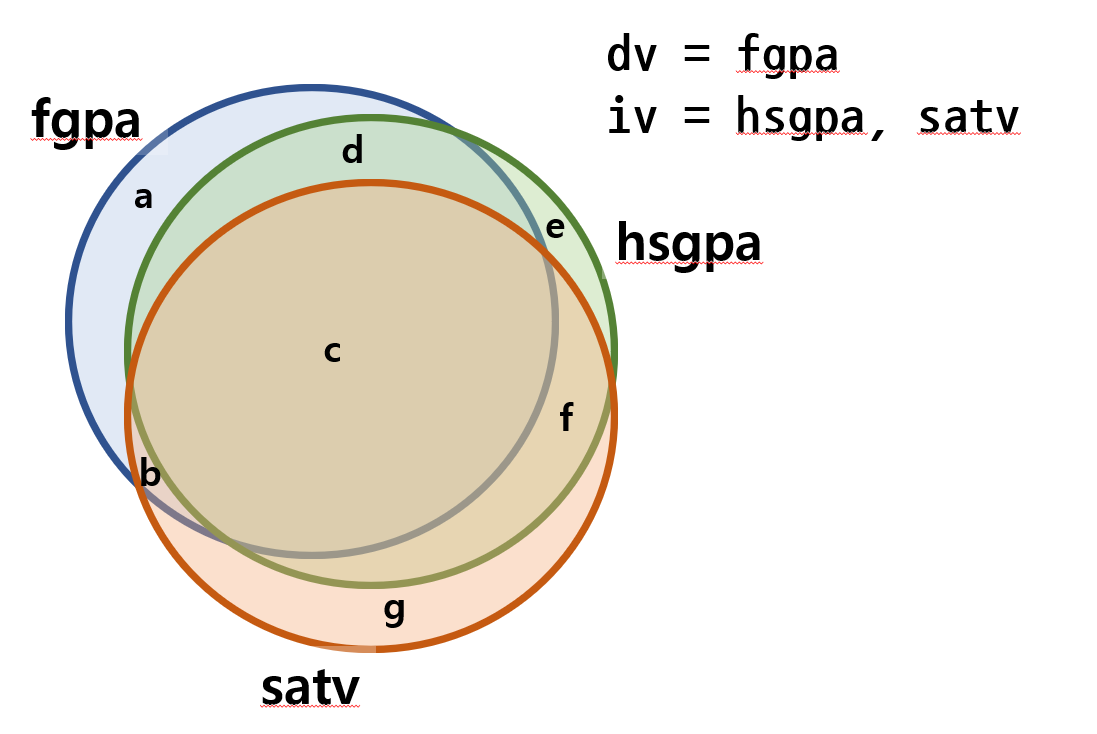
위에서 estimate 값인 0.04064가 위의 R-square 값에 square root값을 씌운 값이 된다. 이를 그림으로 나타내 보면 아래와 같다.
반대의 경우도 실행을 해보면 즉, SATV의 영향력을 제어한 후, HSGPA의 영향력만을 볼 때
n1 <- lm(FGPA ~ SATV) n2 <- lm(HSGPA ~ SATV) res.n1 <- resid(n1) res.n2 <- resid(n2) n.12 <- lm(res.n1 ~ res.n2) summary(n.12)
> n1 <- lm(FGPA ~ SATV)
> n2 <- lm(HSGPA ~ SATV)
> res.n1 <- resid(n1)
> res.n2 <- resid(n2)
> n.12 <- lm(res.n1 ~ res.n2)
> summary(n.12)
Call:
lm(formula = res.n1 ~ res.n2)
Residuals:
Min 1Q Median 3Q Max
-0.2431 -0.1125 -0.0286 0.1269 0.2716
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.04e-18 5.67e-02 0.00 1.000
res.n2 8.45e-01 2.65e-01 3.18 0.013 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.179 on 8 degrees of freedom
Multiple R-squared: 0.559, Adjusted R-squared: 0.504
F-statistic: 10.1 on 1 and 8 DF, p-value: 0.0129
>
이제는 그 R-squared 값이 0.559임을 알게 되었다. 이의 제곱근은 $\sqrt{0.559} = 0.7477$ 이고, 이것이 SATV의 영향력을 IV, DV 모두에게서 제거한 후에 IV의 (HSGPA만의) 영향력을 보는 방법이라는 것을 안다.
pcor.test(FGPA, HSGPA, SATV)
> pcor.test(FGPA, HSGPA, SATV) estimate p.value statistic n gp Method 1 0.7476 0.02057 2.978 10 1 pearson >
위의 도식화된 분석으로 R의 multiple regression에서의 한 변인에 대한 t-test는 그 변인을 제외한 다른 IV들을 콘트롤하여 해당 IV와 DV에서 제거한 후에 본다는 사실을 알 수 있다. 즉, lm(FGPA~SATV+HSGPA) 에서 독립변인 SATV의 t값은 HSGPA의 영향력을 제거하여 제어한 후에 살펴보고 이를 반영한다는 것을 말한다.
또한 위의 설명은 다른 곳에서 언급했던 Multiple regression에서의 summary(lm())과 anova(lm())이 차이를 보이는 이유를 설명하기도 한다 (여기서는 summary(mod)와 anova(mod)). anova는 변인을 순서대로 받고 다른 IV들에 대한 제어를 하지 않으므로 IV 순서에 따라서 그 분석 결과가 달라지기도 한다.
아래의 결과를 살펴보면 anova() 결과 독립변인들의 p value 들과 summary() 에서의 독립변인들의 p value가 다른 이유가 다르다.
# anova()에서의 결과 acs_k3 1 110211 110211 32.059 2.985e-08 *** # summary(lm())에서의 결과 acs_k3 3.3884 2.3333 1.452 0.147
아래는 Multiple Regression 설명에서 가져옴
dvar <- read.csv("http://commres.net/wiki/_media/elemapi2_.csv", fileEncoding="UTF-8-BOM")
mod <- lm(api00 ~ ell + acs_k3 + avg_ed + meals, data=dvar)
summary(mod)
anova(mod)
> dvar <- read.csv("http://commres.net/wiki/_media/elemapi2_.csv", fileEncoding="UTF-8-BOM")
> mod <- lm(api00 ~ ell + acs_k3 + avg_ed + meals, data=dvar)
> summary(mod)
Call:
lm(formula = api00 ~ ell + acs_k3 + avg_ed + meals, data = dvar)
Residuals:
Min 1Q Median 3Q Max
-187.020 -40.358 -0.313 36.155 173.697
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 709.6388 56.2401 12.618 < 2e-16 ***
ell -0.8434 0.1958 -4.307 2.12e-05 ***
acs_k3 3.3884 2.3333 1.452 0.147
avg_ed 29.0724 6.9243 4.199 3.36e-05 ***
meals -2.9374 0.1948 -15.081 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 58.63 on 374 degrees of freedom
(21 observations deleted due to missingness)
Multiple R-squared: 0.8326, Adjusted R-squared: 0.8308
F-statistic: 465 on 4 and 374 DF, p-value: < 2.2e-16
> anova(mod)
Analysis of Variance Table
Response: api00
Df Sum Sq Mean Sq F value Pr(>F)
ell 1 4502711 4502711 1309.762 < 2.2e-16 ***
acs_k3 1 110211 110211 32.059 2.985e-08 ***
avg_ed 1 998892 998892 290.561 < 2.2e-16 ***
meals 1 781905 781905 227.443 < 2.2e-16 ***
Residuals 374 1285740 3438
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
아래에서 mod2를 보면
- api00이 종속변인이고,
- ell, avg_ed, meals + acs_k3 가 독립변인인데,
- 그 순서가 이전 문서의
- ell, acs_k3, avg_ed, meals에서 바뀐것을 알 수 있다 (acs.k3가 맨 뒤로 감).
- 즉,
- lm(api00 ~ ell + acs_k3 + avg_ed + meals)
- lm(api00 ~ ell + avg_ed + meals + acs_k3)
anova는 독립변인에 대한 영향력을 다른 IV들을 고려하지 않고, 그냥 입력 순서대로 처리하므로, acs_k3를 마지막으로 보냄으로써, 다른 IV들이 DV에 대한 설명력을 모두 차지하고 그 나머지를 보여주게 된다.
> mod2 <- lm(api00 ~ ell + avg_ed + meals + acs_k3, data=dvar)
> summary(mod2)
Call:
lm(formula = api00 ~ ell + avg_ed + meals + acs_k3, data = dvar)
Residuals:
Min 1Q Median 3Q Max
-186.90 -40.13 -0.07 35.96 174.12
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 711.681 56.468 12.60 < 2e-16 ***
ell -0.845 0.197 -4.28 2.4e-05 ***
avg_ed 28.966 6.947 4.17 3.8e-05 ***
meals -2.948 0.196 -15.02 < 2e-16 ***
acs_k3 3.336 2.340 1.43 0.15
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 58.8 on 371 degrees of freedom
Multiple R-squared: 0.832, Adjusted R-squared: 0.831
F-statistic: 461 on 4 and 371 DF, p-value: <2e-16
>
> anova(mod2)
Analysis of Variance Table
Response: api00
Df Sum Sq Mean Sq F value Pr(>F)
ell 1 4502711 4502711 1309.762 <2e-16 ***
avg_ed 1 1017041 1017041 295.840 <2e-16 ***
meals 1 866716 866716 252.113 <2e-16 ***
acs_k3 1 7250 7250 2.109 0.1473
Residuals 374 1285740 3438
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
이는 다른 독립변인들의 순서를 바꾸어도 마찬가지이다. mod3은 mod2에서 meals변인을 맨 앞으로 옮긴 예이다. 즉
- mod ← lm(api00 ~ ell + acs_k3 + avg_ed + meals)
- mod2 ← lm(api00 ~ ell + avg_ed + meals + acs_k3)
- mod3 ← lm(api00 ~ meals + ell + avg_ed + acs_k3)
summary(mod), summary(mod2), summary(mod3)의 결과는 서로 다르지 않지만, anova의 결과는 어떤 독립변인이 앞으로 오는가에 따라서 그 f값과 p-value가 달라진다. 물론, 만약에 독립변인들 간의 상관관계가 0이라면 순서가 영향을 주지는 않겠다.
> mod3 <- lm(api00 ~ meals + ell + avg_ed + acs_k3, data=dvar)
> summary(mod3)
Call:
lm(formula = api00 ~ meals + ell + avg_ed + acs_k3, data = dvar)
Residuals:
Min 1Q Median 3Q Max
-186.90 -40.13 -0.07 35.96 174.12
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 711.681 56.468 12.60 < 2e-16 ***
meals -2.948 0.196 -15.02 < 2e-16 ***
ell -0.845 0.197 -4.28 2.4e-05 ***
avg_ed 28.966 6.947 4.17 3.8e-05 ***
acs_k3 3.336 2.340 1.43 0.15
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 58.8 on 371 degrees of freedom
Multiple R-squared: 0.832, Adjusted R-squared: 0.831
F-statistic: 461 on 4 and 371 DF, p-value: <2e-16
> anova(mod2)
Analysis of Variance Table
Response: api00
Df Sum Sq Mean Sq F value Pr(>F)
ell 1 4480281 4480281 1297.34 <2e-16 ***
avg_ed 1 1014175 1014175 293.67 <2e-16 ***
meals 1 864080 864080 250.21 <2e-16 ***
acs_k3 1 7021 7021 2.03 0.15
Residuals 371 1281224 3453
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
>
> anova(mod3)
Analysis of Variance Table
Response: api00
Df Sum Sq Mean Sq F value Pr(>F)
meals 1 6219897 6219897 1801.08 < 2e-16 ***
ell 1 82758 82758 23.96 1.5e-06 ***
avg_ed 1 55880 55880 16.18 7.0e-05 ***
acs_k3 1 7021 7021 2.03 0.15
Residuals 371 1281224 3453
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
e.g. Using ppcor.test with 4 var
rm(list=ls())
library(ggplot2)
library(dplyr)
library(tidyr)
library(faux)
set.seed(101)
scholar <- rnorm_multi(n = 50,
mu = c(3.12, 3.3, 540, 650),
sd = c(.25, .34, 12, 13),
r = c(0.15, 0.44, 0.47, 0.55, 0.45, 0.88),
varnames = c("HSGPA", "FGPA", "SATV", "GREV"),
empirical = FALSE)
attach(scholar)
# library(psych)
describe(scholar) # provides descrptive information about each variable
corrs <- cor(scholar) # find the correlations and set them into an object called 'corrs'
corrs # print corrs
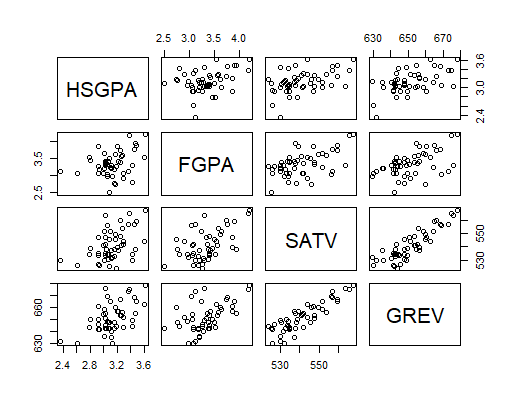
pairs(scholar) # pairwise scatterplots
# install.packages("ppcor")
library(ppcor)
reg.g.sh <- lm(GREV ~ SATV + HSGPA)
res.g.sh <- resid(reg.g.sh)
reg.g.fh <- lm(GREV ~ FGPA + HSGPA)
res.g.fh <- resid(reg.g.fh)
reg.g.sf <- lm(GREV ~ SATV + FGPA)
res.g.sf <- resid(reg.g.sf)
reg.f.sh <- lm(FGPA ~ SATV + HSGPA) # second regression
res.f <- resid(reg.f.sh) # second set of residuals - FGPA free of SATV and HSGPA
reg.s.fh <- lm(SATV ~ FGPA + HSGPA)
res.s <- resid(reg.s.fh)
reg.h.sf <- lm(HSGPA ~ FGPA + SATV)
res.h <- resid(reg.h.sf)
reg.all <- lm(GREV ~ HSGPA + FGPA + SATV)
reg.1 <- lm(GREV ~ res.f)
reg.2 <- lm(GREV ~ res.s)
reg.3 <- lm(GREV ~ res.h)
summary(reg.all)
summary(reg.1)
summary(reg.2)
summary(reg.3)
reg.1a <- lm(res.g.sh~res.f)
reg.2a <- lm(res.g.fh~res.s)
reg.3a <- lm(res.g.sf~res.h)
reg.1$coefficient[2]
reg.2$coefficient[2]
reg.3$coefficient[2]
reg.1a$coefficient[2]
reg.2a$coefficient[2]
reg.3a$coefficient[2]
spr.y.f <- spcor.test(GREV, FGPA, scholar[,c("SATV", "HSGPA")])
spr.y.s <- spcor.test(GREV, SATV, scholar[,c("HSGPA", "FGPA")])
spr.y.h <- spcor.test(GREV, HSGPA, scholar[,c("SATV", "FGPA")])
spr.y.f$estimate
spr.y.s$estimate
spr.y.h$estimate
spr.y.f$estimate^2
spr.y.s$estimate^2
spr.y.h$estimate^2
summary(reg.1)$r.square
summary(reg.2)$r.square
summary(reg.3)$r.square
ca <- summary(reg.1)$r.square +
summary(reg.2)$r.square +
summary(reg.3)$r.square
# so common explanation area should be
summary(reg.all)$r.square - carm(list=ls())
library(ggplot2)
library(dplyr)
library(tidyr)
library(faux)
set.seed(101)
scholar <- rnorm_multi(n = 50,
mu = c(3.12, 3.3, 540, 650),
sd = c(.25, .34, 12, 13),
r = c(0.15, 0.44, 0.47, 0.55, 0.45, 0.88),
varnames = c("HSGPA", "FGPA", "SATV", "GREV"),
empirical = FALSE)
attach(scholar)
# library(psych)
describe(scholar) # provides descrptive information about each variable
corrs <- cor(scholar) # find the correlations and set them into an object called 'corrs'
corrs # print corrs
pairs(scholar) # pairwise scatterplots
# install.packages("ppcor")
library(ppcor)
reg.f.sh <- lm(FGPA ~ SATV + HSGPA) # second regression
res.f <- resid(reg.f.sh) # second set of residuals - FGPA free of SATV and HSGPA
reg.s.fh <- lm(SATV ~ FGPA + HSGPA)
res.s <- resid(reg.s.fh)
reg.h.sf <- lm(HSGPA ~ FGPA + SATV)
res.h <- resid(reg.h.sf)
reg.all <- lm(GREV ~ HSGPA + FGPA + SATV)
reg.1 <- lm(GREV ~ res.f)
reg.2 <- lm(GREV ~ res.s)
reg.3 <- lm(GREV ~ res.h)
summary(reg.all)
summary(reg.1)
summary(reg.2)
summary(reg.3)
reg.1$coefficient[2]
reg.2$coefficient[2]
reg.3$coefficient[2]
spr.y.f <- spcor.test(GREV, FGPA, scholar[,c("SATV", "HSGPA")])
spr.y.s <- spcor.test(GREV, SATV, scholar[,c("HSGPA", "FGPA")])
spr.y.h <- spcor.test(GREV, HSGPA, scholar[,c("SATV", "FGPA")])
spr.y.f$estimate
spr.y.s$estimate
spr.y.h$estimate
spr.y.f$estimate^2
spr.y.s$estimate^2
spr.y.h$estimate^2
summary(reg.1)$r.square
summary(reg.2)$r.square
summary(reg.3)$r.square
ca <- summary(reg.1)$r.square +
summary(reg.2)$r.square +
summary(reg.3)$r.square
# so common explanation area should be
summary(reg.all)$r.square - ca
>
> rm(list=ls())
>
> library(ggplot2)
> library(dplyr)
> library(tidyr)
> library(faux)
>
> set.seed(101)
> scholar <- rnorm_multi(n = 50,
+ mu = c(3.12, 3.3, 540, 650),
+ sd = c(.25, .34, 12, 13),
+ r = c(0.15, 0.44, 0.47, 0.55, 0.45, 0.88),
+ varnames = c("HSGPA", "FGPA", "SATV", "GREV"),
+ empirical = FALSE)
> attach(scholar)
The following objects are masked from scholar (pos = 3):
FGPA, GREV, HSGPA, SATV
>
> # library(psych)
> describe(scholar) # provides descrptive information about each variable
vars n mean sd median trimmed mad min max range skew
HSGPA 1 50 3.13 0.24 3.11 3.13 0.16 2.35 3.62 1.26 -0.42
FGPA 2 50 3.34 0.35 3.32 3.33 0.33 2.50 4.19 1.68 0.27
SATV 3 50 541.28 11.43 538.45 540.50 10.85 523.74 567.97 44.24 0.58
GREV 4 50 651.72 11.90 649.70 651.29 10.55 629.89 678.33 48.45 0.35
kurtosis se
HSGPA 1.21 0.03
FGPA -0.01 0.05
SATV -0.60 1.62
GREV -0.54 1.68
>
> corrs <- cor(scholar) # find the correlations and set them into an object called 'corrs'
> corrs # print corrs
HSGPA FGPA SATV GREV
HSGPA 1.0000 0.3404 0.4627 0.5406
FGPA 0.3404 1.0000 0.5266 0.5096
SATV 0.4627 0.5266 1.0000 0.8802
GREV 0.5406 0.5096 0.8802 1.0000
>
> pairs(scholar) # pairwise scatterplots
>
> # install.packages("ppcor")
> library(ppcor)
>
> reg.f.sh <- lm(FGPA ~ SATV + HSGPA) # second regression
> res.f <- resid(reg.f.sh) # second set of residuals - FGPA free of SATV and HSGPA
>
> reg.s.fh <- lm(SATV ~ FGPA + HSGPA)
> res.s <- resid(reg.s.fh)
>
> reg.h.sf <- lm(HSGPA ~ FGPA + SATV)
> res.h <- resid(reg.h.sf)
>
> reg.all <- lm(GREV ~ HSGPA + FGPA + SATV)
> reg.1 <- lm(GREV ~ res.f)
> reg.2 <- lm(GREV ~ res.s)
> reg.3 <- lm(GREV ~ res.h)
>
> summary(reg.all)
Call:
lm(formula = GREV ~ HSGPA + FGPA + SATV)
Residuals:
Min 1Q Median 3Q Max
-13.541 -3.441 0.148 4.823 7.796
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 180.2560 40.3988 4.46 5.2e-05 ***
HSGPA 8.3214 3.8050 2.19 0.034 *
FGPA 1.3994 2.6311 0.53 0.597
SATV 0.8143 0.0867 9.40 2.8e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.51 on 46 degrees of freedom
Multiple R-squared: 0.799, Adjusted R-squared: 0.786
F-statistic: 60.8 on 3 and 46 DF, p-value: 4.84e-16
> summary(reg.1)
Call:
lm(formula = GREV ~ res.f)
Residuals:
Min 1Q Median 3Q Max
-21.76 -8.65 -2.08 7.83 26.10
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 651.72 1.70 383.59 <2e-16 ***
res.f 1.40 5.74 0.24 0.81
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12 on 48 degrees of freedom
Multiple R-squared: 0.00124, Adjusted R-squared: -0.0196
F-statistic: 0.0595 on 1 and 48 DF, p-value: 0.808
> summary(reg.2)
Call:
lm(formula = GREV ~ res.s)
Residuals:
Min 1Q Median 3Q Max
-22.54 -4.94 -1.24 6.08 20.35
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 651.715 1.332 489.4 < 2e-16 ***
res.s 0.814 0.148 5.5 1.4e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.42 on 48 degrees of freedom
Multiple R-squared: 0.386, Adjusted R-squared: 0.374
F-statistic: 30.2 on 1 and 48 DF, p-value: 1.45e-06
> summary(reg.3)
Call:
lm(formula = GREV ~ res.h)
Residuals:
Min 1Q Median 3Q Max
-22.71 -9.32 -1.30 7.92 26.43
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 651.72 1.68 387.43 <2e-16 ***
res.h 8.32 8.21 1.01 0.32
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 11.9 on 48 degrees of freedom
Multiple R-squared: 0.0209, Adjusted R-squared: 0.000538
F-statistic: 1.03 on 1 and 48 DF, p-value: 0.316
>
> reg.1$coefficient[2]
res.f
1.399
> reg.2$coefficient[2]
res.s
0.8143
> reg.3$coefficient[2]
res.h
8.321
>
> spr.y.f <- spcor.test(GREV, FGPA, scholar[,c("SATV", "HSGPA")])
> spr.y.s <- spcor.test(GREV, SATV, scholar[,c("HSGPA", "FGPA")])
> spr.y.h <- spcor.test(GREV, HSGPA, scholar[,c("SATV", "FGPA")])
>
> spr.y.f$estimate
[1] 0.03519
> spr.y.s$estimate
[1] 0.6217
> spr.y.h$estimate
[1] 0.1447
>
> spr.y.f$estimate^2
[1] 0.001238
> spr.y.s$estimate^2
[1] 0.3865
> spr.y.h$estimate^2
[1] 0.02094
>
> summary(reg.1)$r.square
[1] 0.001238
> summary(reg.2)$r.square
[1] 0.3865
> summary(reg.3)$r.square
[1] 0.02094
>
> ca <- summary(reg.1)$r.square +
+ summary(reg.2)$r.square +
+ summary(reg.3)$r.square
> # so common explanation area should be
> summary(reg.all)$r.square - ca
[1] 0.39
>
multiple regression 분석을 보면 독립변인의 coefficient 값은 각각
- HSGPA 8.3214
- FGPA 1.3994
- SATV 0.8143
이 기울기에 대해서 t-test를 각각 하여 HSGPA와 FGPA의 설명력이 significant 한지를 확인하였다. 그리고 이 때의 R2 값은
- 0.799 이었다.
그런데 이 coefficient값은 독립변인 각각의 고유의 설명력을 가지고 (spcor.test(GREV, x1, 나머지제어)로 얻은 부분) 종속변인에 대해서 regression을 하여 얻은 coefficient값과 같음을 알 수 있다. 즉, multiple regression의 독립변인의 b coefficient 값들은 고유의 설명부분을 (spr) 추출해서 y에 (GREV) regression한 결과와 같음을 알 수 있다.
또한 세 독립변인이 공통적으로 설명하는 부분은
- 0.39
임을 알 수 있다.
e.g., 독립변인 들이 서로 독립적일 때의 각각의 설명력
In this example, the two IVs are orthogonal to each other (not correlated with each other). Hence, regress res.y.x2 against x1 would not result in any problem.
n <- 32 set.seed(182) u <-matrix(rnorm(2*n), ncol=2) u0 <- cbind(u[,1] - mean(u[,1]), u[,2] - mean(u[,2])) x <- svd(u0)$u eps <- rnorm(n) y <- x %*% c(0.05, 1) + eps * 0.01 x1 <- x[,1] x2 <- x[,2] dset <- data.frame(y,x1,x2) head(dset)
y x1 x2 1 0.2311 -0.42320 0.2536 2 -0.1708 -0.13428 -0.1573 3 0.1617 0.12404 0.1580 4 0.1111 0.10377 0.1214 5 0.2176 0.08796 0.1962 6 0.2054 0.02187 0.1950 >
round(cor(dset), 3)
y x1 x2 y 1.000 0.068 0.996 x1 0.068 1.000 0.000 x2 0.996 0.000 1.000 >
lm.y.x1 <- lm(y ~ x1) summary(lm.y.x1)
Call:
lm(formula = y ~ x1)
Residuals:
Min 1Q Median 3Q Max
-0.3750 -0.1013 -0.0229 0.1402 0.2985
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.00258 0.03242 -0.08 0.94
x1 0.06895 0.18341 0.38 0.71
Residual standard error: 0.183 on 30 degrees of freedom
Multiple R-squared: 0.00469, Adjusted R-squared: -0.0285
F-statistic: 0.141 on 1 and 30 DF, p-value: 0.71
lm.y.x1x2 <- lm(y ~ x1 + x2) summary(lm.y.x1x2)
Call:
lm(formula = y ~ x1 + x2)
Residuals:
Min 1Q Median 3Q Max
-0.026697 -0.004072 0.000732 0.006664 0.017220
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.00258 0.00168 -1.54 0.14
x1 0.06895 0.00949 7.27 5.3e-08 ***
x2 1.00328 0.00949 105.72 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.00949 on 29 degrees of freedom
Multiple R-squared: 0.997, Adjusted R-squared: 0.997
F-statistic: 5.61e+03 on 2 and 29 DF, p-value: <2e-16
>
lm.y.x2 <- lm(y ~ x2) summary(lm.y.x2)
Call:
lm(formula = y ~ x2)
Residuals:
Min 1Q Median 3Q Max
-0.027366 -0.010654 0.002941 0.009922 0.027470
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.002576 0.002770 -0.93 0.36
x2 1.003276 0.015669 64.03 <2e-16 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01567 on 30 degrees of freedom
Multiple R-squared: 0.9927, Adjusted R-squared: 0.9925
F-statistic: 4100 on 1 and 30 DF, p-value: < 2.2e-16
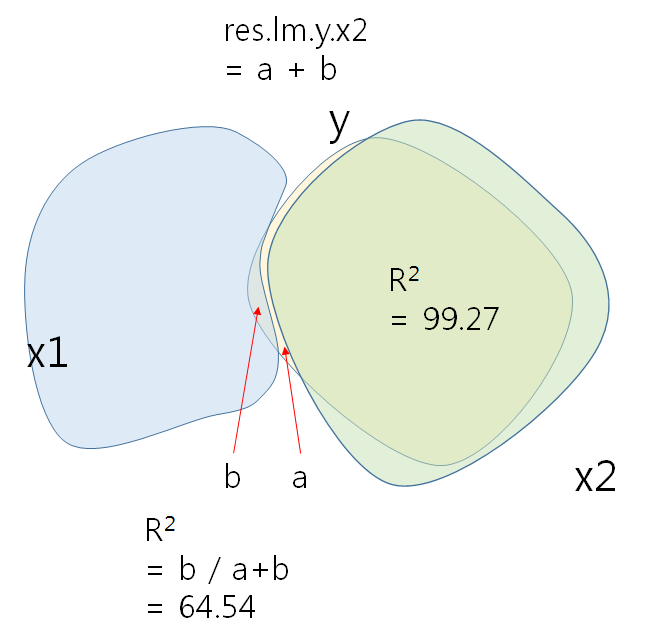
res.lm.y.x2 <- lm.y.x2$resdiduals
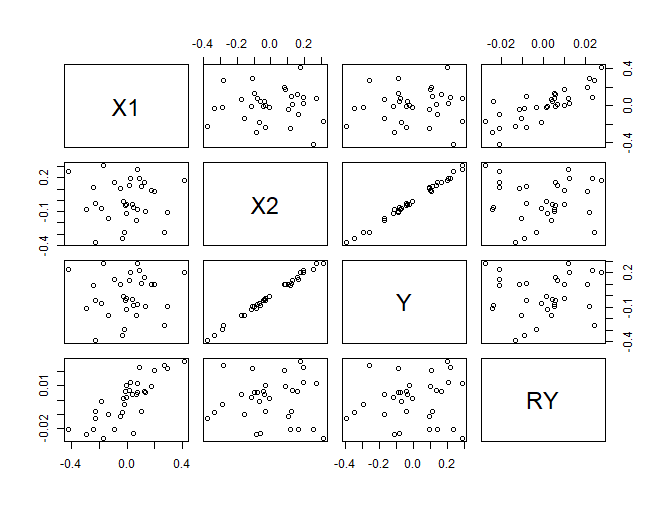
d <- data.frame(X1=x1, X2=x2, Y=y, RY=res.lm.y.x2) plot(d)
> 1-0.9927 [1] 0.0073
X2이 설명하는 Y분산의 나머지를 (1-R2 = 0.0073) 종속변인으로 하고 x1을 독립변인으로 하여 regression을 하면 figure의 RY축에 해당하는 관계가 나타난다. 특히 RY와 X1과의 관계가 선형적으로 바뀐것은 X1 자체로는 아무런 역할을 하지 못하는 것으로 나타나다가, X2가 개입되고 X2의 영향력으로 설명된 Y부분을 제외한 (제어한, controlling) 나머지에 대한 X1의 설명력이 significant하게 바뀐 결과이다.
> lm.resyx2.x1 <- lm(lm.y.x2$residuals ~ x1)
> summary(lm.resyx2.x1)
Call:
lm(formula = lm.y.x2$residuals ~ x1)
Residuals:
Min 1Q Median 3Q Max
-0.0266967 -0.0040718 0.0007323 0.0066643 0.0172201
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.220e-18 1.649e-03 0.00 1
x1 6.895e-02 9.331e-03 7.39 3.11e-08 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.009331 on 30 degrees of freedom
Multiple R-squared: 0.6454, Adjusted R-squared: 0.6336
F-statistic: 54.61 on 1 and 30 DF, p-value: 3.115e-08
>
Actual correlation would look like the below.
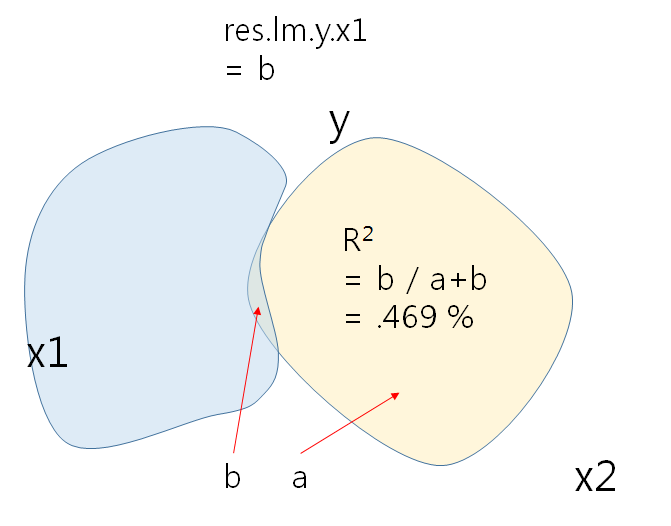
x1의 영향력은 y 총분산에 비해 크지 않다 (b / a + b = .469%)
x2의 영향력을 control한 후에 x1영향력을 보면 64.54%에 달하게 된다.
X1과 X2 간의 상관관계가 심할 때 Regression 결과의 오류
RSS = 3:10 # 오른 발 사이즈 LSS = rnorm(RSS, RSS, 0.1) # 왼발 사이즈 - 오른 발과 매우 유사 cor(LSS, RSS) # correlation ~ 0.99 weights = 120 + rnorm(RSS, 10*RSS, 10) # Fit a joint model m <- lm(weights ~ LSS + RSS) ## F-value is very small, but neither LSS or RSS are significant summary(m) ## Fitting RSS or LSS separately gives a significant result. summary(lm(weights ~ LSS)) ## or summary(lm(weights ~ RSS))
> RSS = 3:10 #Right shoe size
> LSS = rnorm(RSS, RSS, 0.1) #Left shoe size - similar to RSS
> cor(LSS, RSS) #correlation ~ 0.99
[1] 0.9994836
>
> weights = 120 + rnorm(RSS, 10*RSS, 10)
>
> ##Fit a joint model
> m = lm(weights ~ LSS + RSS)
>
> ##F-value is very small, but neither LSS or RSS are significant
> summary(m)
Call:
lm(formula = weights ~ LSS + RSS)
Residuals:
1 2 3 4 5 6 7 8
4.8544 4.5254 -3.6333 -7.6402 -0.2467 -3.1997 -5.2665 10.6066
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 104.842 8.169 12.834 5.11e-05 ***
LSS -14.162 35.447 -0.400 0.706
RSS 26.305 35.034 0.751 0.487
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.296 on 5 degrees of freedom
Multiple R-squared: 0.9599, Adjusted R-squared: 0.9439
F-statistic: 59.92 on 2 and 5 DF, p-value: 0.000321
>
> ##Fitting RSS or LSS separately gives a significant result.
> summary(lm(weights ~ LSS))
Call:
lm(formula = weights ~ LSS)
Residuals:
Min 1Q Median 3Q Max
-6.055 -4.930 -2.925 4.886 11.854
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 103.099 7.543 13.67 9.53e-06 ***
LSS 12.440 1.097 11.34 2.81e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.026 on 6 degrees of freedom
Multiple R-squared: 0.9554, Adjusted R-squared: 0.948
F-statistic: 128.6 on 1 and 6 DF, p-value: 2.814e-05
>
>
> ## or
> summary(lm(weights ~ RSS))
Call:
lm(formula = weights ~ RSS)
Residuals:
Min 1Q Median 3Q Max
-13.46 -4.44 1.61 4.53 9.51
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 125.92 8.76 14.38 7.1e-06 ***
RSS 9.33 1.27 7.34 0.00033 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8.24 on 6 degrees of freedom
Multiple R-squared: 0.9, Adjusted R-squared: 0.883
F-statistic: 53.9 on 1 and 6 DF, p-value: 0.000327
>
e. g. API00 data using ppcor package
This part is an extension of the R example in Multiple Regression.
We are going to use spcor for identifying the effect of each IV. In order to do that, we need to reconstruct the data with the involved variable.
dvar <- read.csv("http://commres.net/wiki/_media/elemapi2_.csv", fileEncoding="UTF-8-BOM")
mod <- lm(api00 ~ ell + acs_k3 + avg_ed + meals, data=dvar)
summary(mod)
anova(mod)
attach(dvar)
da1 <- data.frame(api00, ell, acs_k3, avg_ed, meals)
da2 <- data.frame(api00, ell, avg_ed, meals)
da1 <- na.omit(da1)
da2 <- na.omit(da2)
spcor(da1)
spcor(da2)
> spcor(da1)
$estimate
api00 ell acs_k3 avg_ed meals
api00 1.00000000 -0.09112026 0.03072660 0.08883450 -0.3190889
ell -0.13469956 1.00000000 0.06086724 -0.06173591 0.1626061
acs_k3 0.07245527 0.09709299 1.00000000 -0.13288465 -0.1367842
avg_ed 0.12079565 -0.05678795 -0.07662825 1.00000000 -0.2028836
meals -0.29972194 0.10332189 -0.05448629 -0.14014709 1.0000000
$p.value
api00 ell acs_k3 avg_ed meals
api00 0.000000e+00 0.07761805 0.5525340 0.085390280 2.403284e-10
ell 8.918743e-03 0.00000000 0.2390272 0.232377348 1.558141e-03
acs_k3 1.608778e-01 0.05998819 0.0000000 0.009891503 7.907183e-03
avg_ed 1.912418e-02 0.27203887 0.1380449 0.000000000 7.424903e-05
meals 3.041658e-09 0.04526574 0.2919775 0.006489783 0.000000e+00
$statistic
api00 ell acs_k3 avg_ed meals
api00 0.000000 -1.769543 0.5945048 1.724797 -6.511264
ell -2.628924 0.000000 1.1793030 -1.196197 3.187069
acs_k3 1.404911 1.886603 0.0000000 -2.592862 -2.670380
avg_ed 2.353309 -1.100002 -1.4862899 0.000000 -4.006914
meals -6.075665 2.008902 -1.0552823 -2.737331 0.000000
$n
[1] 379
$gp
[1] 3
$method
[1] "pearson"
> spcor(da2)
$estimate
api00 ell avg_ed meals
api00 1.0000000 -0.08988307 0.08485896 -0.3350062
ell -0.1331295 1.00000000 -0.07018696 0.1557097
avg_ed 0.1164280 -0.06501592 1.00000000 -0.1967128
meals -0.3170300 0.09948710 -0.13568145 1.0000000
$p.value
api00 ell avg_ed meals
api00 0.000000e+00 0.08053412 0.099035570 2.160270e-11
ell 9.465897e-03 0.00000000 0.172705169 2.366624e-03
avg_ed 2.340012e-02 0.20663211 0.000000000 1.158869e-04
meals 2.698723e-10 0.05296417 0.008170237 0.000000e+00
$statistic
api00 ell avg_ed meals
api00 0.000000 -1.752306 1.653628 -6.903560
ell -2.608123 0.000000 -1.366153 3.060666
avg_ed 2.276102 -1.265057 0.000000 -3.895587
meals -6.490414 1.941321 -2.659047 0.000000
$n
[1] 381
$gp
[1] 2
$method
[1] "pearson"
>
e.g. mpg model in mtcars (in r)
partial_and_semipartial_correlation.txt · Last modified: 2024/10/17 10:28 by hkimscil