Table of Contents
Dummy variables in Multiple Regression
datavar <- read.csv("http://commres.net/wiki/_media/r/elemapi2.csv", fileEncoding="UTF-8-BOM")
위는 미국 초등학교 학생의 API 결과와 학교에 대한 (측정단위) 정보를 포함하는 데이터이다. 변인의 정보는 아래와 같다.
Variable Labels Variable Position Label snum 1 school number dnum 2 district number api00 3 api 2000 (school의 2000년도 api 평균점수) api99 4 api 1999 (1999년도 점수) growth 5 growth 1999 to 2000 (두 년도 점수의 차이) meals 6 pct free meals (무료급식의 %) ell 7 english language learners (영어가 모국어가 아닌 학생 수) yr_rnd 8 year round school (무방학학교여부 0 = 방학있음 1 = 방학없음) mobility 9 pct 1st year in school acs_k3 10 avg class size k-3 acs_46 11 avg class size 4-6 not_hsg 12 parent not hsg hsg 13 parent hsg some_col 14 parent some college col_grad 15 parent college grad grad_sch 16 parent grad school avg_ed 17 avg parent ed full 18 pct full credential emer 19 pct emer credential enroll 20 number of students mealcat 21 Percentage free meals in 3 categories collcat 22 <none> Variables in the working file yr_rnd: 0 = 방학있음 1 = 방학없음 mealcat: 1 = 0-46% free meals 2 = 47-80 3 = 81-100
- pct (%) of emer (emergency) credentials: Some states will grant an emergency certificate or permit at the request of a school district that has posted and failed to find a qualified candidate for a teacher vacancy. It typically allows the candidate to serve in a temporary capacity for the duration of a school year.
- pct (%) of full credentials: To be fully certified, it generally means that a teacher must have graduated from an accredited college, completed an approved teacher credential program and passed a test of their academic skills.
위의 각각의 변인 yr_rnd 그리고 mealcat 을 독립변인으로 하고 종속변인을 api00 으로 하여 simple regression을 한다. 그리고 이후 이 둘을 모두 이용하여 multiple regression을 한다. 즉,
mod1 ← lm(api00 ~ yr_rnd, data = datavar)mod2 ← lm(api00 ~ mealcat, data = datavar)mod3 ← lm(api00 ~ yr_rnd + mealcat, data = datavar)mod4 ← lm(api00 ~ yr_rnd * mealcat, data = datavar)
위에서 마지막 두 분석은 interaction을 포함하고 하지 않는 차이이다. 특히 마지막은 아래와 같은 효과를 갖는다
mod4 ← lm(api00 ~ yr_rnd + mealcat + yr_rnd:mealcat, data = datavar)
mod1 <- lm(api00 ~ yr_rnd, data = datavar)
분석에 앞서 str(datavar)의 결과를 보면 yr_rnd 변인과 mealcat 변인이 모두 integer 임을 알 수 있다. 사실은 category variable 이므로 (factor), factor 명령어를 써서 factor 변인으로 바꾸어 준다.
> str(datavar) 'data.frame': 400 obs. of 22 variables: $ snum : int 906 889 887 876 888 4284 4271 2910 2899 2887 ... $ dnum : int 41 41 41 41 41 98 98 108 108 108 ... $ api00 : int 693 570 546 571 478 858 918 831 860 737 ... $ api99 : int 600 501 472 487 425 844 864 791 838 703 ... $ growth : int 93 69 74 84 53 14 54 40 22 34 ... $ meals : int 67 92 97 90 89 10 5 2 5 29 ... $ ell : int 9 21 29 27 30 3 2 3 6 15 ... $ yr_rnd : int 0 0 0 0 0 0 0 0 0 0 ... $ mobility: int 11 33 36 27 44 10 16 44 10 17 ... $ acs_k3 : int 16 15 17 20 18 20 19 20 20 21 ... $ acs_46 : int 22 32 25 30 31 33 28 31 30 29 ... $ not_hsg : int 0 0 0 36 50 1 1 0 2 8 ... $ hsg : int 0 0 0 45 50 8 4 4 9 25 ... $ some_col: int 0 0 0 9 0 24 18 16 15 34 ... $ col_grad: int 0 0 0 9 0 36 34 50 42 27 ... $ grad_sch: int 0 0 0 0 0 31 43 30 33 7 ... $ avg_ed : num NA NA NA 1.91 1.5 3.89 4.13 4.06 3.96 2.98 ... $ full : int 76 79 68 87 87 100 100 96 100 96 ... $ emer : int 24 19 29 11 13 0 0 2 0 7 ... $ enroll : int 247 463 395 418 520 343 303 1513 660 362 ... $ mealcat : int 2 3 3 3 3 1 1 1 1 1 ... $ collcat : int 1 1 1 1 1 2 2 2 2 3 ...
> datavar$yr_rnd <- factor(datavar$yr_rnd, levels = c(0, 1), labels = c("break", "no_break"))
> datavar$mealcat <- factor(datavar$mealcat, levels = c(1, 2, 3), labels = c("0-46", "47-80", "81-100"))
> str(datavar)
'data.frame': 400 obs. of 22 variables:
$ snum : int 906 889 887 876 888 4284 4271 2910 2899 2887 ...
$ dnum : int 41 41 41 41 41 98 98 108 108 108 ...
$ api00 : int 693 570 546 571 478 858 918 831 860 737 ...
$ api99 : int 600 501 472 487 425 844 864 791 838 703 ...
$ growth : int 93 69 74 84 53 14 54 40 22 34 ...
$ meals : int 67 92 97 90 89 10 5 2 5 29 ...
$ ell : int 9 21 29 27 30 3 2 3 6 15 ...
$ yr_rnd : Factor w/ 2 levels "break","no_break": 1 1 1 1 1 1 1 1 1 1 ...
$ mobility: int 11 33 36 27 44 10 16 44 10 17 ...
$ acs_k3 : int 16 15 17 20 18 20 19 20 20 21 ...
$ acs_46 : int 22 32 25 30 31 33 28 31 30 29 ...
$ not_hsg : int 0 0 0 36 50 1 1 0 2 8 ...
$ hsg : int 0 0 0 45 50 8 4 4 9 25 ...
$ some_col: int 0 0 0 9 0 24 18 16 15 34 ...
$ col_grad: int 0 0 0 9 0 36 34 50 42 27 ...
$ grad_sch: int 0 0 0 0 0 31 43 30 33 7 ...
$ avg_ed : num NA NA NA 1.91 1.5 3.89 4.13 4.06 3.96 2.98 ...
$ full : int 76 79 68 87 87 100 100 96 100 96 ...
$ emer : int 24 19 29 11 13 0 0 2 0 7 ...
$ enroll : int 247 463 395 418 520 343 303 1513 660 362 ...
$ mealcat : Factor w/ 3 levels "0-46","47-80",..: 2 3 3 3 3 1 1 1 1 1 ...
$ collcat : int 1 1 1 1 1 2 2 2 2 3 ...
>
>
> head(datavar)
snum dnum api00 api99 growth meals ell yr_rnd mobility acs_k3 acs_46 not_hsg hsg
1 906 41 693 600 93 67 9 break 11 16 22 0 0
2 889 41 570 501 69 92 21 break 33 15 32 0 0
3 887 41 546 472 74 97 29 break 36 17 25 0 0
4 876 41 571 487 84 90 27 break 27 20 30 36 45
5 888 41 478 425 53 89 30 break 44 18 31 50 50
6 4284 98 858 844 14 10 3 break 10 20 33 1 8
some_col col_grad grad_sch avg_ed full emer enroll mealcat collcat
1 0 0 0 NA 76 24 247 47-80 1
2 0 0 0 NA 79 19 463 81-100 1
3 0 0 0 NA 68 29 395 81-100 1
4 9 9 0 1.91 87 11 418 81-100 1
5 0 0 0 1.50 87 13 520 81-100 1
6 24 36 31 3.89 100 0 343 0-46 2
> mod <- lm(api00 ~ yr_rnd, data=datavar)
> summary(mod)
Call:
lm(formula = api00 ~ yr_rnd, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-273.539 -95.662 0.967 103.341 297.967
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 684.54 7.14 95.88 <2e-16 ***
yr_rndno_break -160.51 14.89 -10.78 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 125.3 on 398 degrees of freedom
Multiple R-squared: 0.226, Adjusted R-squared: 0.2241
F-statistic: 116.2 on 1 and 398 DF, p-value: < 2.2e-16
>
>
회귀분석의 예측식은 (regression model) 다음과 같다.
y hat = 684.54 - 160.51(yr_rndno_break)
- yr_rndno_break: yr_rndno_break = 1
- y hat = 684.54 - 160.51 * (1)
- y hat = 524.03
- yr_rndbreak: yr_rndnobreak = 0
- y hat = 684.54 - 160.51 * (0)
- y hat = 684.54
위 회귀식에서 r은
y hat = a + bX 의 형식에서 X 로 no_break를 썼음을 (yr_rndno_break) 알 수 있다. 이 경우에는 yr_rndno_break를 1로 넣어서 해석을 한다. 즉, no break일 경우에는 y hat = 684.54 - 160.51(1) 이라는 것이다. 반대로 break일 경우에는 뒤쪽 부분이 해당이 안되므로 0으로 대체한다. 따라서 이 경우의 회귀식은 y hat = 684.54이다. 이 둘을 비교해보면 no break일 경우에는
y hat = 684.54 - 160.51(1) = 524.03 이고
break일 경우에는
y hat = 684.54 - 160.51(0) = 684.54 라는 것이다. 다시 이야기하면 break가 없는 학교의 평균 api점수는 524.03점인 반면에 break가 있는 학교의 평균은 684.54 이다. 이 점수의 차이는 두 집단의 평균을 비교하는 것과 같은 형태를 (형식) 갖는다. 즉,
t.test(api00 ~ yr_rnd, data=datavar) 를 테스트하는 것과 마찬가지이다.
> t.test(api00 ~ yr_rnd, data=datavar, var.equal=T)
Two Sample t-test
data: api00 by yr_rnd
t = 10.782, df = 398, p-value < 2.2e-16
alternative hypothesis: true difference in means between group break and group no_break is not equal to 0
95 percent confidence interval:
131.2390 189.7737
sample estimates:
mean in group break mean in group no_break
684.5390 524.0326
>
## 위에서 두 그룹의 평균은 각각 684.5390 와 524.0326 이다.
## 분석에서 t 값이 10.782 이고 p-value = 2.2e-16 이다.
## 이것은 회귀분석에서의 t-test 값과 같다.
mod2 <- lm(api00 ~ mealcat, data = datavar)
> mod2 <- lm(api00 ~ mealcat, data=datavar)
> summary(mod2)
Call:
lm(formula = api00 ~ mealcat, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-253.394 -47.883 0.282 52.282 185.620
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 805.718 6.169 130.60 <2e-16 ***
mealcat47-80 -166.324 8.708 -19.10 <2e-16 ***
mealcat81-100 -301.338 8.629 -34.92 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 70.61 on 397 degrees of freedom
Multiple R-squared: 0.7548, Adjusted R-squared: 0.7536
F-statistic: 611.1 on 2 and 397 DF, p-value: < 2.2e-16
>
>
y hat = 805.718 - 166.324*mealcat47-80 - 301.338*mealcat81-100 mealcat0-46 (mg1 으로 대체) mealcat47-80 (mg2 으로 대체) maelcat81-100 (mg3 으로 대체)
이에 대한 해석도 앞에서의 것과 마찬가지이다.
- y hat = 805.718 - 166.324*mg2 - 301.338*mg3
- mg1 = 1, mg2 = 0, mg3 = 0 일 경우
- y hat = 805.718 - 166.324*(0) - 301.338*(0)
- y hat = 805.718
- mg1 = 0, mg2 = 1, mg3 = 0 일 경우
- y hat = 805.718 - 166.324*(1) - 301.338*(0)
- y hat = 805.718 - 166.324
- y hat = 639.394
- mg1 = 0, mg2 = 0, mg3 = 1 일 경우
- y hat = 805.718 - 166.324*(0) - 301.338*(1)
- y hat = 805.718 - 301.338
- y hat = 504.38
- 즉, 무료급식의 퍼센티지가 높을 수록 api점수가 낮음을 알 수 있다. 이렇게 무료급식 퍼센티지를 독립변인으로 종속변인인 api00점수를 (학력점수) 봤을 때, 그 설명력이 통계학적으로 유효한가는 regression output에서 (summary(mod2))
- F-value 와 p-value를 가지고 판단한다.
- (F (2, 397) = 611.1; p-value < 2.2e-16)
- 위에서 2, 397 은 각각 between degrees of freedom 과 within degrees of freedom 이다. 이를 보고도 우리는
- 총 400개의 학교가 데이터에 참여했음을 알 수 있고 (2 + 397 에 1을 더한 값),
- 독립변인의 종류가 3가지 (df = 2 이므로) 임을 알 수 있다.
- R square value 는 설명력의 크기를 알려준다.
- 0.7548 즉, 75.48% 를 독립변인이 종속변인을 설명한다 (상당한 크기임을 알 수 있다).
mod3 ← lm(api00 ~ yr_rnd + mealcat, data = datavar)
> mod3 <- lm(api00 ~ yr_rnd + mealcat, data=datavar)
> summary(mod3)
Call:
lm(formula = api00 ~ yr_rnd + mealcat, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-215.32 -49.50 1.65 49.17 183.63
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 808.013 6.040 133.777 < 2e-16 ***
yr_rndno_break -42.960 9.362 -4.589 5.99e-06 ***
mealcat47-80 -163.737 8.515 -19.229 < 2e-16 ***
mealcat81-100 -281.683 9.446 -29.821 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 68.89 on 396 degrees of freedom
Multiple R-squared: 0.7672, Adjusted R-squared: 0.7654
F-statistic: 435 on 3 and 396 DF, p-value: < 2.2e-16
>
예측식은 아래와 같다.
y hat = 808.013 + -42.960*(yr_rndno_break) + -163.737(mealcat47-80) + -281.683(mealcat81-100) yr_rnd: break = 방학있음 no_break = 방학없음 mealcat: 0-46% free meals 47-80% 81-100%
이에 대한 해석은 각각의 독립변인의 종류 수인 2개와 3개를 곱한 6개의 경우로 나누어서 생각할 수 있다. 즉,
y hat = 808.013 + -42.960*(yr_rndno_break) + -163.737(mealcat47-80) + -281.683(mealcat81-100)
을 바탕으로 각각의 조건을 고려하여 y hat를 계산하면 아래와 같다.
TABLE. Two dummy variables
| mealcat0-46 | mealcat47-80 | mealcat81-100 | |
|---|---|---|---|
| yr_rndbreak | yr_rndbreak = 1 yr_rndno_break = 0 mealcat0-46 = 1 mealcat47-80 = 0 mealcat81-100 = 0 경우 y hat = 808.013 | yr_rndbreak = 1 yr_rndno_break = 0 mealcat0-46 = 0 mealcat47-80 = 1 mealcat81-100 = 0 경우 y hat = 808.013 - 163.737 = 644.276 | yr_rndbreak = 1 yr_rndno_break = 0 mealcat0-46 = 0 mealcat47-80 = 0 mealcat81-100 = 1 경우 y hat = 808.013 - 281.683 = 526.33 |
| yr_rndno_break | yr_rndbreak = 0 yr_rndno_break = 1 mealcat0-46 = 1 mealcat47-80 = 0 mealcat81-100 = 0 경우 y hat = 808.013 - 42.960 = 765.053 | yr_rndbreak = 0 yr_rndno_break = 1 mealcat0-46 = 0 mealcat47-80 = 1 mealcat81-100 = 0 경우 y hat = 808.013 - 42.960 - 163.737 = 601.316 | yr_rndbreak = 0 yr_rndno_break = 1 mealcat0-46 = 0 mealcat47-80 = 0 mealcat81-100 = 1 경우 y hat = 808.013 - 42.960 - 281.683 = 483.37 |
mod4 ← lm(api00 ~ yr_rnd * mealcat, data = datavar)
> mod4 <- lm(api00 ~ yr_rnd + mealcat + yr_rnd:mealcat, data=datavar)
> summary(mod4)
Call:
lm(formula = api00 ~ yr_rnd + mealcat + yr_rnd:mealcat, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-207.533 -50.764 -1.843 48.874 179.000
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 809.685 6.185 130.911 < 2e-16 ***
yr_rndno_break -74.257 26.756 -2.775 0.00578 **
mealcat47-80 -164.412 8.877 -18.522 < 2e-16 ***
mealcat81-100 -288.193 10.443 -27.597 < 2e-16 ***
yr_rndno_break:mealcat47-80 22.517 32.752 0.687 0.49217
yr_rndno_break:mealcat81-100 40.764 29.231 1.395 0.16394
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 68.87 on 394 degrees of freedom
Multiple R-squared: 0.7685, Adjusted R-squared: 0.7656
F-statistic: 261.6 on 5 and 394 DF, p-value: < 2.2e-16
위의 테스트는 두 개의 독립변인이 모두 종류이고 종속변인이 숫자일 때의 조건을 만족하니 factorial anova를 해도 된다. 아래는 그 결과이다.
> mod4 <- lm(api00 ~ yr_rnd + mealcat + yr_rnd:mealcat, data=datavar)
> summary(mod4)
Call:
lm(formula = api00 ~ yr_rnd + mealcat + yr_rnd:mealcat, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-207.533 -50.764 -1.843 48.874 179.000
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 809.685 6.185 130.911 < 2e-16 ***
yr_rndno_break -74.257 26.756 -2.775 0.00578 **
mealcat47-80 -164.412 8.877 -18.522 < 2e-16 ***
mealcat81-100 -288.193 10.443 -27.597 < 2e-16 ***
yr_rndno_break:mealcat47-80 22.517 32.752 0.687 0.49217
yr_rndno_break:mealcat81-100 40.764 29.231 1.395 0.16394
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 68.87 on 394 degrees of freedom
Multiple R-squared: 0.7685, Adjusted R-squared: 0.7656
F-statistic: 261.6 on 5 and 394 DF, p-value: < 2.2e-16
>
>
> mod5 <- aov(api00 ~ yr_rnd * mealcat, data = datavar)
> summary(mod5)
Df Sum Sq Mean Sq F value Pr(>F)
yr_rnd 1 1825001 1825001 384.736 <2e-16 ***
mealcat 2 4369144 2184572 460.539 <2e-16 ***
yr_rnd:mealcat 2 10584 5292 1.116 0.329
Residuals 394 1868944 4744
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
>
>
인터액션에 대한 해석
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 809.685 6.185 130.911 < 2e-16 ***
yr_rndno_break -74.257 26.756 -2.775 0.00578 **
mealcat47-80 -164.412 8.877 -18.522 < 2e-16 ***
mealcat81-100 -288.193 10.443 -27.597 < 2e-16 ***
yr_rndno_break:mealcat47-80 22.517 32.752 0.687 0.49217
yr_rndno_break:mealcat81-100 40.764 29.231 1.395 0.16394
---
이전 식
y hat = 808.013 + -42.960*(yr_rndno_break) + -163.737(mealcat47-80) + -281.683(mealcat81-100)
위의 식
y hat = 809.685 + -74.257*(yr_rndno_break) +
-164.412*(mealcat47-80) +
-288.193*(mealcat81-100) +
22.517*(yr_rndno_break:mealcat47-80) + --> aaaaa case
40.764*(yr_rndno_break:mealcat81-100) --> bbbbb case
yr_rnd:
break = 방학있음
no_break = 방학없음
mealcat:
0-46% free meals
47-80%
81-100%
| mealcat0-46 | mealcat47-80 | mealcat81-100 | |
|---|---|---|---|
| yr_rndbreak | 베이스라인 yr_rndno_break = 0 mealcat47-80 = 0 mealcat81-100 = 0 경우 y hat = 809.685 | yr_rndno_break = 0 mealcat0-46 = 0 mealcat81-100 = 0 경우 y hat = 809.685 - | yr_rndno_break = 0 mealcat0-46 = 0 mealcat47-80 = 0 경우 y hat = 809.685 - |
| yr_rndno_break | yr_rndbreak = 0 mealcat47-80 = 0 mealcat81-100 = 0 경우 y hat = 809.685 - | aaaaa yr_rndbreak = 0 mealcat0-46 = 0 mealcat81-100 = 0 경우 y hat = 809.685 - | bbbbb yr_rndbreak = 0 mealcat0-46 = 0 mealcat47-80 = 0 경우 y hat = 809.685 - |
마지막 두 케이스를 보면 no_break학교 중에서 밀카테고리 2와 3에서 떨어지는 정도가 어느 정도 완화되는 경향을 보이지만 통계학적으로 significant하지는 않다.
다른 예
> summ(mod4)
MODEL INFO:
Observations: 400
Dependent Variable: api00
Type: OLS linear regression
MODEL FIT:
F(5,394) = 261.61, p = 0.00
R² = 0.77
Adj. R² = 0.77
Standard errors: OLS
--------------------------------------------------------------------
Est. S.E. t val. p
---------------------------------- --------- ------- -------- ------
(Intercept) 809.69 6.18 130.91 0.00
yr_rndno_break -74.26 26.76 -2.78 0.01
mealcat47-80 -164.41 8.88 -18.52 0.00
mealcat81-100 -288.19 10.44 -27.60 0.00
yr_rndno_break:mealcat47-80 22.52 32.75 0.69 0.49
yr_rndno_break:mealcat81-100 40.76 29.23 1.39 0.16
--------------------------------------------------------------------
>
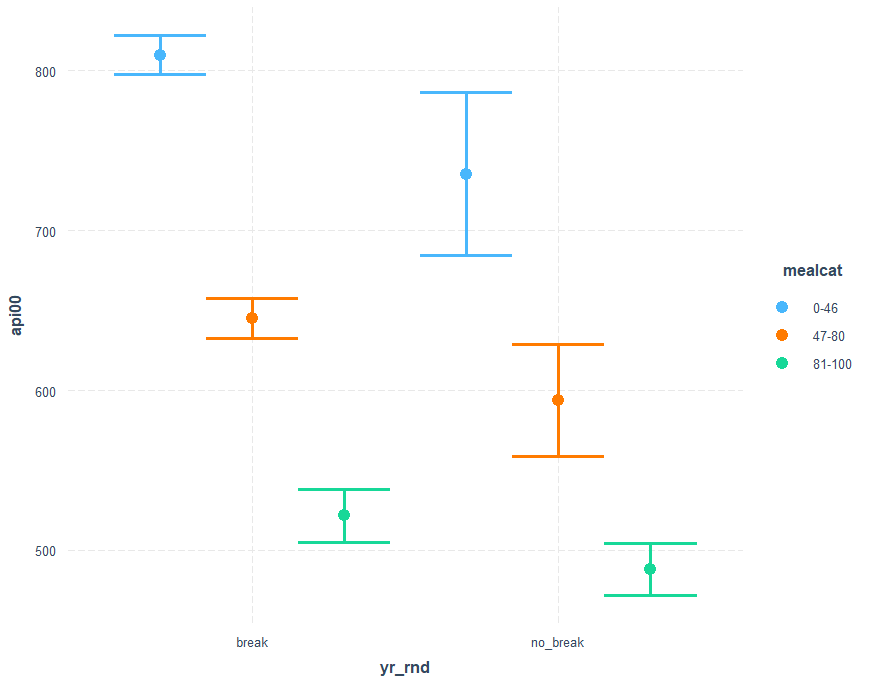
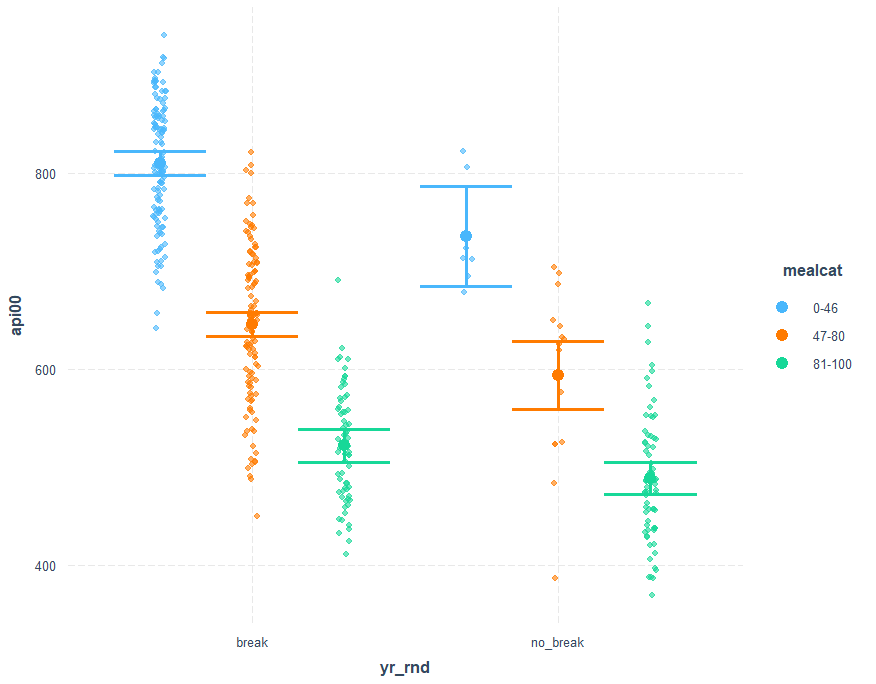
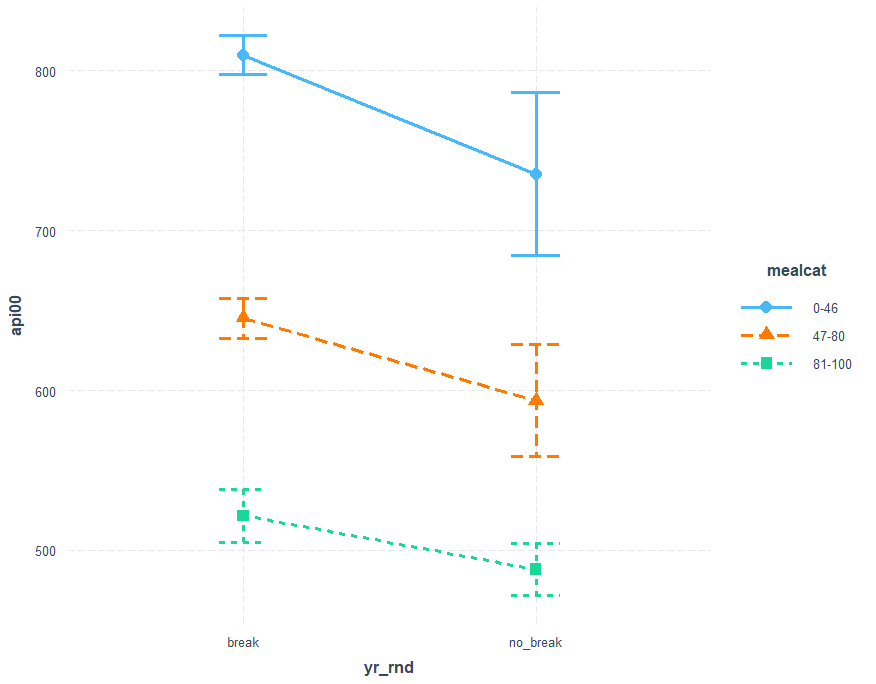
cat_plot(mod4, pred=yr_rnd, modx=mealcat) cat_plot(mod4, pred=yr_rnd, modx=mealcat, plot.points = TRUE)
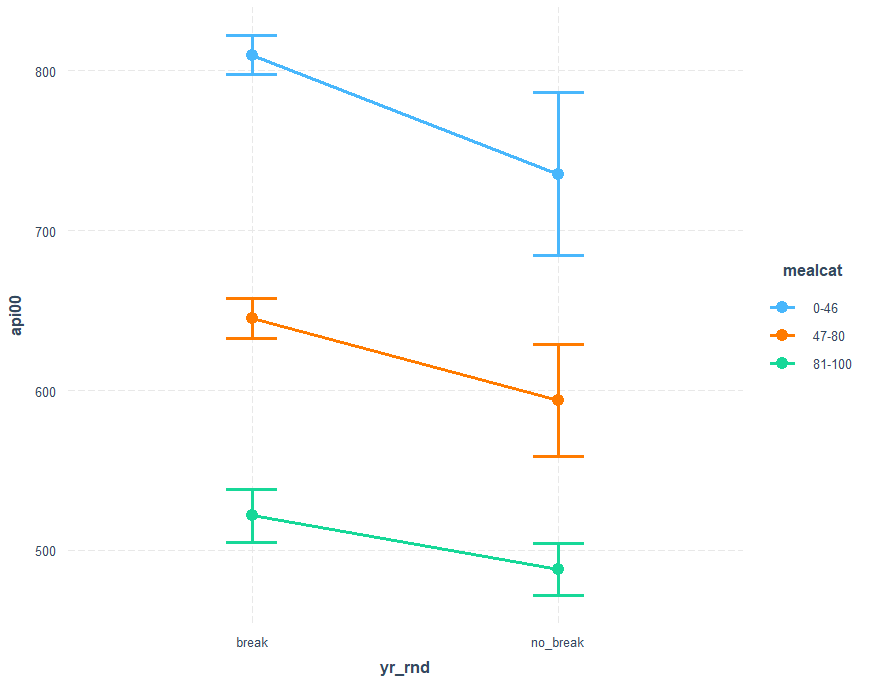
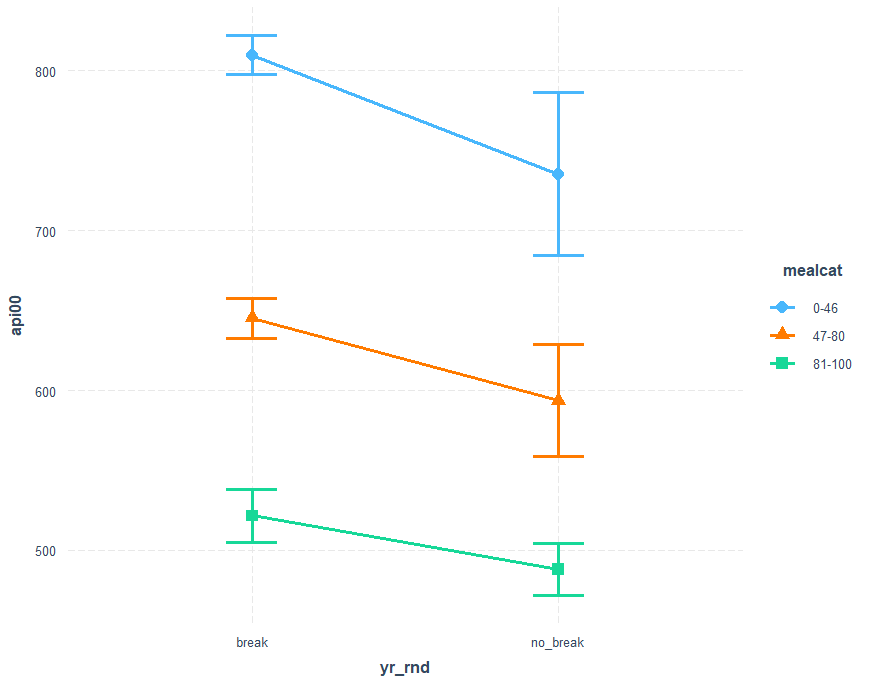
cat_plot(mod4, pred=yr_rnd, modx=mealcat, geom = line) cat_plot(mod4, pred=yr_rnd, modx=mealcat, geom = "line", point.shape = TRUE) cat_plot(mod4, pred=yr_rnd, modx=mealcat, geom = "line", point.shape = TRUE, vary.lty = TRUE)
continus + categorical variables
# dummy variables
datavar <- read.csv("http://commres.net/wiki/_media/r/elemapi2.csv", fileEncoding="UTF-8-BOM")
datavar$yr_rnd <- factor(datavar$yr_rnd, levels = c(0, 1), labels = c("break", "no_break"))
# categorical + continous (종류 + 숫자)
mod5 <- lm(api00 ~ yr_rnd + some_col, data=datavar)
summary(mod5)
> # dummy variables
> datavar <- read.csv("http://commres.net/wiki/_media/r/elemapi2.csv", fileEncoding="UTF-8-BOM")
>
> # categorical + continous (종류 + 숫자)
> mod5 <- lm(api00 ~ yr_rnd + some_col, data=datavar)
> summary(mod5)
Call:
lm(formula = api00 ~ yr_rnd + some_col, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-276.04 -90.83 -5.44 89.18 293.20
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 637.858 13.503 47.24 < 2e-16 ***
yr_rnd -149.159 14.875 -10.03 < 2e-16 ***
some_col 2.236 0.553 4.04 6.3e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 123 on 397 degrees of freedom
Multiple R-squared: 0.257, Adjusted R-squared: 0.253
F-statistic: 68.5 on 2 and 397 DF, p-value: <2e-16
categorical + continuous with interaction effects
# dummy variables
datavar <- read.csv("http://commres.net/wiki/_media/r/elemapi2.csv", fileEncoding="UTF-8-BOM")
datavar$yr_rnd <- factor(datavar$yr_rnd, levels = c(0, 1), labels = c("break", "no_break"))
str(datavar)
# categorical + continous (종류 + 숫자) mod5 <- lm(api00 ~ yr_rnd + some_col, data=datavar) summary(mod5)
# interaction effects = categorical + continous (종류 + 숫자) mod6 <- lm(api00 ~ yr_rnd + some_col + yr_rnd:some_col, data=datavar) # mod6 <- lm(api00 ~ yr_rnd * some_col, data=datavar) summary(mod6)
anova(mod5, mod6)
coef(mod6) intcept.break <- coef(mod6)[1] intcept.nobreak <- coef(mod6)[1] + coef(mod6)[2] intcept.break intcept.nobreak slope.break <- coef(mod6)[3] slope.nobreak <- coef(mod6)[4] slope.break slope.nobreak
output
plot(api00 ~ some_col, data = datavar,
col = as.numeric(yr_rnd), pch = as.numeric(yr_rnd) )
abline(intcept.nobreak, slope.nobreak, col = 1, lty = 1, lwd = 2) # line for foreign cars
abline(intcept.break, slope.break, col = 2, lty = 2, lwd = 2) # line for domestic cars
legend("bottomright", c("no_break", "break"), pch = c(1, 2), col = c(1, 2))
> # dummy variables
> datavar <- read.csv("http://commres.net/wiki/_media/r/elemapi2.csv", fileEncoding="UTF-8-BOM")
> datavar$yr_rnd <- factor(datavar$yr_rnd, levels = c(0, 1), labels = c("break", "no_break"))
> str(datavar)
'data.frame': 400 obs. of 22 variables:
$ snum : int 906 889 887 876 888 4284 4271 2910 2899 2887 ...
$ dnum : int 41 41 41 41 41 98 98 108 108 108 ...
$ api00 : int 693 570 546 571 478 858 918 831 860 737 ...
$ api99 : int 600 501 472 487 425 844 864 791 838 703 ...
$ growth : int 93 69 74 84 53 14 54 40 22 34 ...
$ meals : int 67 92 97 90 89 10 5 2 5 29 ...
$ ell : int 9 21 29 27 30 3 2 3 6 15 ...
$ yr_rnd : Factor w/ 2 levels "break","no_break": 1 1 1 1 1 1 1 1 1 1 ...
$ mobility: int 11 33 36 27 44 10 16 44 10 17 ...
$ acs_k3 : int 16 15 17 20 18 20 19 20 20 21 ...
$ acs_46 : int 22 32 25 30 31 33 28 31 30 29 ...
$ not_hsg : int 0 0 0 36 50 1 1 0 2 8 ...
$ hsg : int 0 0 0 45 50 8 4 4 9 25 ...
$ some_col: int 0 0 0 9 0 24 18 16 15 34 ...
$ col_grad: int 0 0 0 9 0 36 34 50 42 27 ...
$ grad_sch: int 0 0 0 0 0 31 43 30 33 7 ...
$ avg_ed : num NA NA NA 1.91 1.5 3.89 4.13 4.06 3.96 2.98 ...
$ full : int 76 79 68 87 87 100 100 96 100 96 ...
$ emer : int 24 19 29 11 13 0 0 2 0 7 ...
$ enroll : int 247 463 395 418 520 343 303 1513 660 362 ...
$ mealcat : int 2 3 3 3 3 1 1 1 1 1 ...
$ collcat : int 1 1 1 1 1 2 2 2 2 3 ...
>
> # categorical + continous (종류 + 숫자)
> mod5 <- lm(api00 ~ yr_rnd + some_col, data=datavar)
> summary(mod5)
Call:
lm(formula = api00 ~ yr_rnd + some_col, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-276.04 -90.83 -5.44 89.18 293.20
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 637.858 13.503 47.24 < 2e-16 ***
yr_rndno_break -149.159 14.875 -10.03 < 2e-16 ***
some_col 2.236 0.553 4.04 6.3e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 123 on 397 degrees of freedom
Multiple R-squared: 0.257, Adjusted R-squared: 0.253
F-statistic: 68.5 on 2 and 397 DF, p-value: <2e-16
> # interaction effects = categorical + continous (종류 + 숫자)
> mod6 <- lm(api00 ~ yr_rnd + some_col + yr_rnd:some_col, data=datavar)
> # mod6 <- lm(api00 ~ yr_rnd * some_col, data=datavar)
> summary(mod6)
Call:
lm(formula = api00 ~ yr_rnd + some_col + yr_rnd:some_col, data = datavar)
Residuals:
Min 1Q Median 3Q Max
-275.12 -87.85 -0.57 90.74 279.25
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 655.110 14.035 46.68 < 2e-16 ***
yr_rndno_break -248.071 29.859 -8.31 1.6e-15 ***
some_col 1.409 0.586 2.41 0.01655 *
yr_rndno_break:some_col 5.993 1.577 3.80 0.00017 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 121 on 396 degrees of freedom
Multiple R-squared: 0.283, Adjusted R-squared: 0.277
F-statistic: 52.1 on 3 and 396 DF, p-value: <2e-16
>
> anova(mod5, mod6) Analysis of Variance Table Model 1: api00 ~ yr_rnd + some_col Model 2: api00 ~ yr_rnd + some_col + yr_rnd:some_col Res.Df RSS Df Sum of Sq F Pr(>F) 1 397 6001470 2 396 5790327 1 211144 14.4 0.00017 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 >
> coef(mod6)
(Intercept) yr_rndno_break some_col
655.110 -248.071 1.409
yr_rndno_break:some_col
5.993
> intcept.break <- coef(mod6)[1]
> intcept.nobreak <- coef(mod6)[1] + coef(mod6)[2]
> intcept.break
(Intercept)
655.1
> intcept.nobreak
(Intercept)
407
> slope.break <- coef(mod6)[3]
> slope.nobreak <- coef(mod6)[4]
> slope.break
some_col
1.409
> slope.nobreak
yr_rndno_break:some_col
5.993
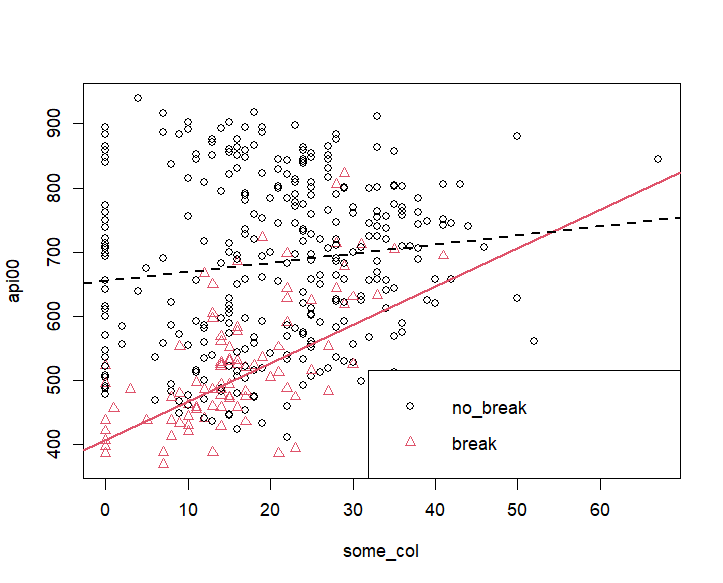
> plot(api00 ~ some_col, data = datavar,
+ col = as.numeric(yr_rnd), pch = as.numeric(yr_rnd) )
> abline(intcept.nobreak, slope.nobreak, col = 1, lty = 1, lwd = 2) # line for foreign cars
> abline(intcept.break, slope.break, col = 2, lty = 2, lwd = 2) # line for domestic cars
> legend("bottomright", c("no_break", "break"), pch = c(1, 2), col = c(1, 2))
>
>
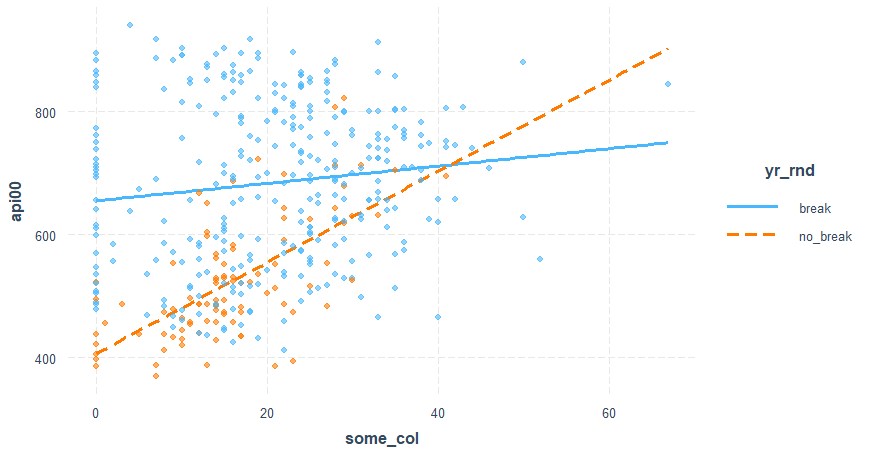
> interact_plot(mod6, pred=some_col, modx=yr_rnd, geom = "line", plot.points = TRUE)