R square value in logistic regression

Logistic regression에서는 linear regression 에서 사용하는 R^2 값을 구할 수는 없다. 따라서 이에 대응하는 개념을 적용하는 여러가지 방법이 개발되어 사용되고 있는데 그 중에서 가장 많이 쓰이는 방법이 McFadden's pseudo R square 이다.

참고로 R square value in linear regression의 경우에는
\begin{align*} R^2 = & \frac {SS_{regression}} {SS_{total}} \\ = & \frac {SS_{total} - SS_{residual}} {SS_{total}} \\ \end{align*}
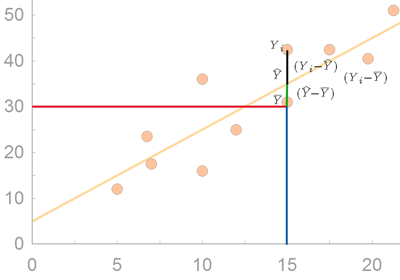
과 같이 구한다. 이는 그림에서 보는 것 처럼 모든 개인들의

검정색과 녹색으로 이루어진 오차의 제곱의 합 중에서, 즉
= 수평선인 평균으로 개인점수를 예측했을 때 일어나는 오차의 제곱의 합 중에서
독립변인인 X의 정보를 취득함으로 인해서 구하게 된
사선의 정보로 (regression line) 예측했을 때 ($\hat{Y} = a + b \cdot X$) 만회된 오차의 (녹색선 부분) 제곱의 합의
비율을 의미한다.
이 사선은 이 비율이 가장 크게 되도록 하는 원리로 구하게 된다. 이 말의 뜻은
만회된 지 못한 나머지 오차의 (residual error) 제곱의 합이 최소값이 되는 선이 선택된다는 뜻이다.
따라서 이렇게 R square 값을 구하는 방법을 Least Squared Method라고 한다.

library(ISLR)