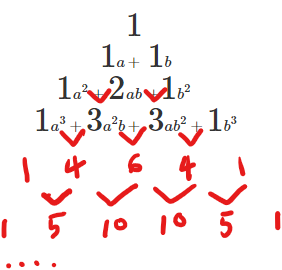Table of Contents
The Binomial Theorem
see this web page
\begin{eqnarray*} (a + b)^{1} & = & (a + b) \\ (a + b)^{2} & = & (a + b)(a + b) \\ (a + b)^{3} & = & (a + b)^{2} (a + b) \\ (a + b)^{4} & = & (a + b)^{3} (a + b) \\ \end{eqnarray*}
\begin{eqnarray*} (a + b)^{1} & = & (a + b) \\ (a + b)^{2} & = & (a + b)(a + b) \\ & = & a^2 + 2ab + b^2 \\ (a + b)^{3} & = & (a^2 + 2ab + b^2)(a + b) \\ & = & a^3 + 3a^2b + 3ab^2 + b^3 \\ (a + b)^{4} & = & (a^3 + 3a^2b + 3ab^2 + b^3)(a + b) \\ & = & a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 \\ \end{eqnarray*}
어떤 패턴이 보인다. 이 패턴을 The Binominal Theorem이라고 하고 아래처럼 표현된다.
\begin{eqnarray*}
(a + b)^{m} & = & \sum^{m}_{y=0}{{m}\choose{y}} a^{y} b^{m-y} \\
\end{eqnarray*}
Pattern
\begin{eqnarray*} (a + b)^{3} & = & (a^2 + 2ab + b^2)(a + b) & = & a^3 + 3a^2b + 3ab^2 + b^3 \\ \end{eqnarray*}
지수의 경우
a의 지수는 3, 2, 1, 0 순으로 내려가고
$$ a^{\huge 3} + 3a^{\huge 2}b + 3a^{\huge 1}b^2 + a^{\huge 0}b^3 $$
b의 지수는 0, 1, 2, 3 순으로 올라간다.
$$ a^3b^{\huge 0} + 3a^2b^{\huge 1} + 3a^1b^{\huge 2} + a^0 b^{\huge 3} $$
이는 아래와 같이 정리할 수 있다.
\begin{align*}
n&=3 \\
k&=0 & k&=1 & k&=2 & k&=3 \\
&a^3 & &a^2 & &a^1 & &1 \\
&1 & &b^1 & &b^2 & &b^3
\end{align*}
\begin{eqnarray*} {\huge a^{n-k}b^{k}} \end{eqnarray*}
계수
\begin{eqnarray*} &1& \\ a &+& b \\ a^2 + 2a&b& + b^2 \\ a^3 + 3a^2b &+& 3ab^2 + b^3 \end{eqnarray*}
\begin{eqnarray*} &{\huge 1}& \\ {\huge 1}a &+& {\huge 1}b \\ {\huge 1}a^2 + {\huge 2}&ab& + {\huge 1}b^2 \\ {\huge 1}a^3 + {\huge 3}a^2b &+& {\huge 3}ab^2 + {\huge 1}b^3 \end{eqnarray*}
따라서 $ (a+b)^4 $는
| a 지수는 4, 3, 2, 1, 0 순 | $a^4$ | $a^3$ | $a^2$ | $a^1$ | 1 |
| b 지수는 0, 1, 2, 3, 4 순 | $a^4$ | $a^3b$ | $a^2b^2$ | $a^1b^3$ | $b^4$ |
| coefficient 는 1, 4, 6, 4, 1 순 | $a^4$ | $4a^3b$ | $6a^2b^2$ | $4a^1b^3$ | $b^4$ |
그렇다면,
$(a + b)^5 = {\text ?} $
\begin{eqnarray*} &{0 \choose 0}& \\ &{1 \choose 0} \; {1 \choose 1}& \\ &{2 \choose 0}\; {2 \choose 1}\; {2 \choose 2}& \\ &{3 \choose 0}\; {3 \choose 1}\; {3 \choose 2}\; {3 \choose 3}& \\ &{4 \choose 0}\; {4 \choose 1}\; {4 \choose 2}\; {4 \choose 3}\; {4 \choose 4}& \\ &{5 \choose 0}\; {5 \choose 1}\; {5 \choose 2}\; {5 \choose 3}\; {5 \choose 4}\; {5 \choose 5} & \\ \end{eqnarray*}
\begin{eqnarray*} & {\large 1} & \\ & {\large 1\quad 1} & \\ & {\large 1\quad 2\quad 1} & \\ & {\large 1\quad 3\quad 3\quad 1} & \\ & {\large 1\quad 4\quad 6\quad 4\quad 1} & \\ & {\large 1\quad 5\quad 10\quad 10\quad 5\quad 1} & \\ \end{eqnarray*}
따라서
\begin{eqnarray*}
& a^5 + a^4 + a^3 + a^2 + a^1 + a^0 & \\
& b^0 + b^1 + b^2 + b^3 + b^4 + b^5 & \\
& 1 + 5 + 10 + 10 + 5 + 1 & \\
& a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5 & \\
\end{eqnarray*}
위를 종합해서 정리하면
\begin{eqnarray*}
\text{The binomial theorem} & & \\
(a + b)^{n} & = & \sum^{n}_{k=0}{{n}\choose{k}} a^{n-k} b^{k} \\
\end{eqnarray*}
예를 들면, 아래와 같다. ($n = 3$ 인경우)
\begin{eqnarray*}
(a + b)^{3} & = & \sum^{3}_{k=0}{{3}\choose{k}} a^{3-k} b^{k} \\
& = & {{3}\choose{0}} a^{3-0} b^{0} + {{3}\choose{1}} a^{3-1} b^{1} + {{3}\choose{2}} a^{3-2} b^{2} + {{3}\choose{3}} a^{3-3} b^{3} \\
& = & 1 \cdot a^{3} b^{0} + 3 \cdot a^{2} b^{1} + 3 \cdot a^{1} b^{2} + 1 \cdot a^{0} b^{3} \\
& = & a^{3} + 3a^{2} b + 3ab^{2} + b^{3}
\end{eqnarray*}