Q. Alcohol이 임산부에게 미치는 영향
: Alcohol이 임산부에게 미치는 영향에 대해서 조사를 하는 연구자가, 임신 중의 alcohol 섭취가 태아의 몸무게에 미치는 영향에 대해서 관심을 가졌다. 이에 따라서 n = 16 의 랜덤 샘플 쥐가 구해졌다. 어미 쥐는 매일 일정량의 alcohol을 섭취하였다. 연구자는 이 쥐들의 새끼 중 하나씩을 선택해서 n = 16의 샘플을 취한 후 평균을 내 보았더니, $\overline{X}$ = 15 grams 이었다. 보통 쥐의 경우 평균 몸무게는 $\mu = 18$ 그램이고 $\sigma = 4$ 라는 것을 연구자는 알고 있다. 연구자는 alcohol의 영향력을 어떻게 테스트해야 할까?
먼저, 가설을 세우도록 한다.
$\displaystyle H(1):\quad \mu_{\tiny{alcohol.exposure}} \neq 18$
위의 가설이 의미하는 것은 “알코올에 노출된 쥐의 평균은 18 gram이 아닐 것이다”이다. 즉, 이상하게 보일지 몰라도 $ (\overline{X} = 15) \neq (\mu = 18) $ 이다. 이를 다시 이야기 하자면 과연 15 gram은 18 gram의 무리에서 나온 15gram 일까 라는 질문이다. 18gram을 평균으로 하는 무리에서 15gram이 나오는 것이 자연스러울까라는 질문과 같다. 이를 증명하기 위한 방법은 없다. . . . 따라서, 위의 선언을 뒤집어서 생각해 본다. 이는 아래와 같이 표현할 수 있다.
$H(0):\quad \mu_{\tiny{alcohol.exposure}} = 18$
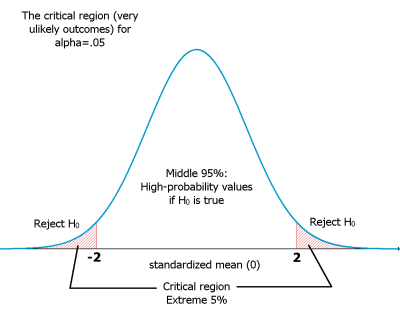
다음으로, 가설 검증의 기준을 세운다. 즉 critical region을 혹은 alpha level을 정한다. 여기서는 alpha = 0.05로 한다. Critical region을 정하기 위해서 취하는 좋은 방법은 우선 $H(0)$ 가 참일 경우에 나타나는 sampling distribution의 그래프를 손으로 그려 보는 것이다.
sample means의 distribution은 정규분포를 이루고 그 standard error의 값은 아래와 같다.
$\displaystyle \sigma_{\overline{X}} = \frac {\sigma}{\sqrt{n}} = \frac{4}{\sqrt{16}}=1$
그리고 이 distribution의 평균값은 $H(0)$ 의 평균값과 같다고 생각한다. 다음으로, 선택되었던 샘플을 이용해서 z-score를 구해본다.
$\displaystyle z = \frac{\overline{X}-\mu}{\sigma_{\overline{X}}} = \frac{15 - 18}{1} = \frac{-3}{1} = -3.00$
다음으로 decision-making을 한다. z-score = -3 은 critical region에 포함 됨으로, 연구자는 샘플의 z-score가 unusual한 것이라고 결론을 내린다. 즉, 연구자는 $H(0)$ 을 부정(reject)하고, 연구가설을 채택한다.
> > 1 - (pnorm(2) - pnorm(-2)) [1] 0.04550026 > 1 - (pnorm(1.96) - pnorm(-1.96)) [1] 0.04999579 >
혹은 아래와 같이 생각해 볼 수도 있다.
> pnorm(-3) [1] 0.001349898 > pnorm(3) - pnorm(-3) [1] 0.9973002 > 1-(pnorm(3) - pnorm(-3)) [1] 0.002699796 >