Table of Contents
Interpretation of Multiple Regression (회귀분석결과 해석)
options(digits = 4)
HSGPA <- c(3.0, 3.2, 2.8, 2.5, 3.2, 3.8, 3.9, 3.8, 3.5, 3.1)
FGPA <- c(2.8, 3.0, 2.8, 2.2, 3.3, 3.3, 3.5, 3.7, 3.4, 2.9)
SATV <- c(500, 550, 450, 400, 600, 650, 700, 550, 650, 550)
scholar <- data.frame(FGPA, HSGPA, SATV) # collect into a data frame
# install.packages("psych")
# library(psych)
describe(scholar) # provides descrptive information about each variable
corrs <- cor(scholar) # find the correlations and set them into an object called 'corrs'
corrs # print corrs
pairs(scholar) # pairwise scatterplots
attach(scholar)
m1 <- lm(FGPA ~ SATV, data = scholar)
summary(m1)
> options(digits = 4)
> HSGPA <- c(3.0, 3.2, 2.8, 2.5, 3.2, 3.8, 3.9, 3.8, 3.5, 3.1)
> FGPA <- c(2.8, 3.0, 2.8, 2.2, 3.3, 3.3, 3.5, 3.7, 3.4, 2.9)
> SATV <- c(500, 550, 450, 400, 600, 650, 700, 550, 650, 550)
>
> scholar <- data.frame(FGPA, HSGPA, SATV) # collect into a data frame
> describe(scholar) # provides descrptive information about each variable
Error in describe(scholar) : could not find function "describe"
>
> corrs <- cor(scholar) # find the correlations and set them into an object called 'corrs'
> corrs # print corrs
FGPA HSGPA SATV
FGPA 1.0000 0.9226 0.8144
HSGPA 0.9226 1.0000 0.8745
SATV 0.8144 0.8745 1.0000
>
> pairs(scholar) # pairwise scatterplots
> attach(scholar)
The following objects are masked _by_ .GlobalEnv:
FGPA, HSGPA, SATV
> m1 <- lm(FGPA ~ SATV, data = scholar)
> summary(m1)
Call:
lm(formula = FGPA ~ SATV, data = scholar)
Residuals:
Min 1Q Median 3Q Max
-0.2804 -0.1305 -0.0566 0.0350 0.6481
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.95633 0.54419 1.76 0.1169
SATV 0.00381 0.00096 3.97 0.0041 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.27 on 8 degrees of freedom
Multiple R-squared: 0.663, Adjusted R-squared: 0.621
F-statistic: 15.8 on 1 and 8 DF, p-value: 0.00412
위 linear modeling 에서 아래와 같은 선형모델을 얻는다.
y hat (FGPA) = 0.95633 + 0.00381 * SATV
- 기본적으로 SAT 점수가 0 일 때 FGPA 는 0.95633 이다 (절편값).
- SAT와 FGPA는 양의 상관관계를 갖는다 (계수 값이 양수이므로).
- SAT 점수 단위가 한점이 올라갈 때마다 FGPA 점수가 0.00381이 올라간다.
- SAT가 100점이 올라가면 GPA는 0.381이 올라간다.
- 아래는 그것을 확인해보는 R 코드이다.
p <- data.frame(c(400,500,600,700,800)) colnames(p) <- "SATV" pred <- predict(m1, p) pred[2]-pred[1] pred[5]-pred[4]
> p <- data.frame(c(400,500,600,700,800))
> colnames(p) <- "SATV"
> pred <- predict(m1, p)
> pred[2]-pred[1]
2
0.381
> pred[5]-pred[4]
5
0.381
아래는 원 데이터를 d 로 바꾼후 독립변인인 SATV를 평균점수를 0으로 하는 SATV_centered 로 바꾸어서 다시 regression을 한 것이다. m1_centered의 결과를 보면
- SATV의 계수 값은 원래와 (m1) 같다.
- 절편값은 3.09 인데, 이는 SATV 점수가 평균일 (mean(SATV) = 560) 때의 FGPA 값을 말한다.
d <- scholar d$SATV_centered <- d$SATV - mean(d$SATV) mean(d$SATV) m1_centered <- lm(FGPA ~ SATV_centered, data=d) summary(m1_centered)
> d <- scholar
> d$SATV_centered <- d$SATV - mean(d$SATV)
> mean(d$SATV)
[1] 560
> m1_centered <- lm(FGPA ~ SATV_centered, data=d)
> summary(m1_centered)
Call:
lm(formula = FGPA ~ SATV_centered, data = d)
Residuals:
Min 1Q Median 3Q Max
-0.2804 -0.1305 -0.0566 0.0350 0.6481
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.09000 0.08531 36.22 3.7e-10 ***
SATV_centered 0.00381 0.00096 3.97 0.0041 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.27 on 8 degrees of freedom
Multiple R-squared: 0.663, Adjusted R-squared: 0.621
F-statistic: 15.8 on 1 and 8 DF, p-value: 0.00412
기울기 계수로 독립변인의 영향력 평가하기
SATV의 기울기 계수인 0.00381은 모델 직선의 (데이터를 관통하는) 위치를 알려주는 것이고 이 선을 중심으로 데이터들이 포진하게 된다. 그리고 선에서 데이터 까지의 거리가 에러 값이다. 또한 이 거리는 표준편차 값을 갖게 되고 이를 이용하여 표준오차 (standard error) 값을 구해볼 수 있다. 즉 이 표준오차 값은 에러값 들이 선을 중심으로 얼마나 잘 포진되어 있는 지를 보여주는 지표가 된다.
이 논리도 연구자는 계수 값을 (b에 해당하는 계수) 표준오차 값으로 (standard error)값으로 나누고 이를 t 계산 값으로 (t-calculated value) 삼아서 significance 테스트를 할 수 있다. 표준오차가 작은 경우는 선을 중심으로 실제 데이터 값들이 좁게 모여 있음을 의미하므로 높은 t 값을 얻을 수 있겠다. 따라서 계수의 역할에 대한 통계학적인 의미가 있다고 판단한다.
> m1 <- lm(FGPA ~ SATV, data = scholar)
> summary(m1)
Call:
lm(formula = FGPA ~ SATV, data = scholar)
Residuals:
Min 1Q Median 3Q Max
-0.2804 -0.1305 -0.0566 0.0350 0.6481
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.95633 0.54419 1.76 0.1169
SATV 0.00381 0.00096 3.97 0.0041 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.27 on 8 degrees of freedom
Multiple R-squared: 0.663, Adjusted R-squared: 0.621
F-statistic: 15.8 on 1 and 8 DF, p-value: 0.00412
위에서 SATV의
- 계수값은 (Estimate) 0.00381 이고 (a라고 하자) 이에 대한
- standard error값은 0.00096 이다 (b라고 하자). 따라서
- t값은 a/b 인 3.97 이 된다.
- t-test의 원리는 그룹 간 차이를 (특별한 종류의) 표준편차로 (이것이 표준오차) 나눈 값임을 기억
- 이 깂이 확률적으로 유의미한 지를 (significant) 보려면
pt(3.97, df = 8, lower.tail = F)를 이용하여 probability를 구한다.- df 값은 n-2로 (변수의 갯수) 구한다.
- 이 값은 0.002059 이고 이는 한 쪽 날개에 해당하는 probability이므로 2를 곱하여
- 0.004119 를 구한다. 이것이 Pr(>|t|) 값인
0.0041혹은0.00412이다.
Standard error of b1
b1은 기울기이다 (regression coefficient). xi 지점에서 y값을 살펴보면 실제 y값에서 (y value) 기울기 선에 위치한 y값을 (y fitted value 혹은 predicted value of y) 뺀 값은 우리가 이야기한 error에 혹은 residual에 해당하는 값이다. 이 에러들이 사선을 중심으로 어떻게 포진해 있는가를 보기 위해서 b1 기울기 주변에 모인 residual 값들의 standard error 값을 알아보려면: residual의 분산값을 x의 Sum of Square 값에 제곱근을 씌운 값으로 나누어 준다. 즉,
\begin{eqnarray*} \displaystyle s_{b_{1}} & = & \sqrt {\frac {MSE}{SS_{X}}} \\ & = & \displaystyle \sqrt { \frac{1}{n-2} * \frac{SSE}{SS_{X}}} \\ & = & \displaystyle \sqrt { \frac{1}{n-2} * \frac{\Sigma{(Y-\hat{Y})^2}}{\Sigma{(X_{i} - \bar{X})^2}}} \\ \end{eqnarray*}
> sum(resid(m1)^2) [1] 0.5822 > sse <- sum(resid(m1)^2) > ssx <- sum((SATV - mean(SATV))^2) > sqrt((1/8)*(sse/ssx)) [1] 0.0009598 >
혼란스러운 것을 정리하기 위해서:
- summary(m1) 아웃풋에서의 standard error of residual 은 말 그대로
- SSE/df(=n-2) 값에 sqrt를 씌워준 값이다.
- 즉 sqrt(에러분산 혹은 레지듀얼분산) 값을 말한다.
- 즉 sqrt(MSE) 값이다.
- b1의 se 값은 b1에 (독립변인의 기울기) 대한 영향력을 테스트하는 b1의 se이다.
- 이 값은 sqrt(MSE/SSX1) 를 이용해서 구한다.
- 만약에 multiple regression이라서 X가 여러개라면 각 X에 해당하는 SSxi 가 분모로 쓰일 것이다.
회귀분석의 조건
- Linearity. 선형관계를 전제로 한다. 즉 이차방정식, 삼차방정식, 로그방정식 등의 관계가 아닌 직선에 기초한 관계이다.
- Normality of residuals. 회귀식을 중심으로 한 에러값 혹은 잔차값의 분포는 정상적이어야 한다.
- Homoscedasticity of the residuals. 에러의 분산 값은 x 값의 range에서 공히 일정해야 한다. homoscedasticity
- No outlier. 숫자로 측정된 데이터의 경우 아웃라이어는 전체 평균치에 (statistics) 큰 영향을 미친다. 따라서 아웃라이어를 확인하고 제외할 필요가 있는지 확인해야 한다.
- 독립변인들 간의 상관관계가 커서는 안된다. 어느정도까지 허용할지는 여러가지 방법이 있다. multicollinearity
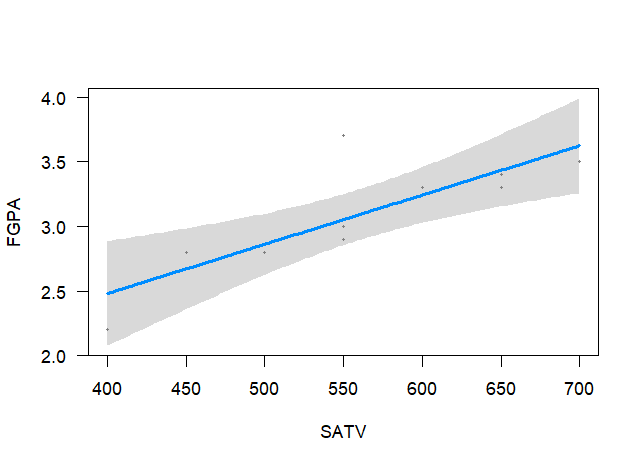
플로팅
library(visreg) visreg(m1)
# load necessary libraries
library(ggpubr)
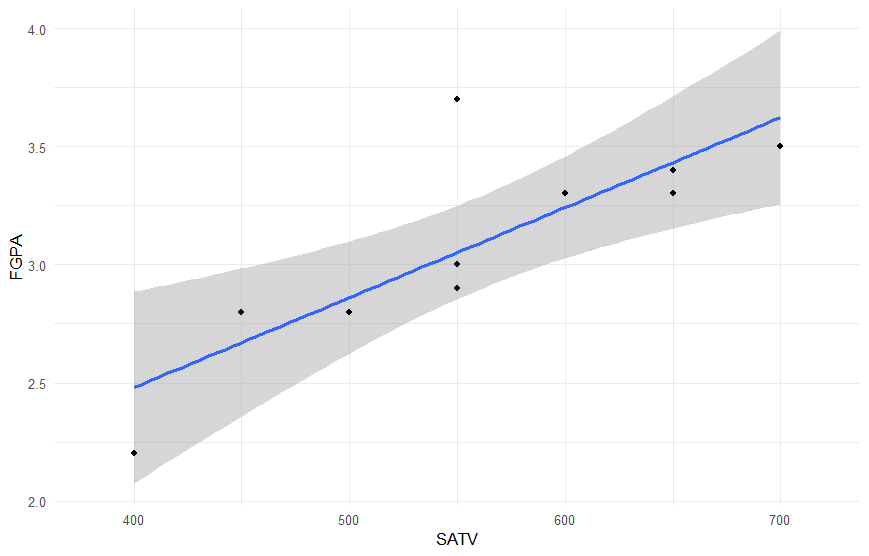
# create plot with regression line, regression equation and R^2
ggplot(scholar, aes(x = SATV, y = FGPA)) +
geom_smooth(method = "lm") +
xlim(380, 720) +
geom_point() +
theme_minimal()
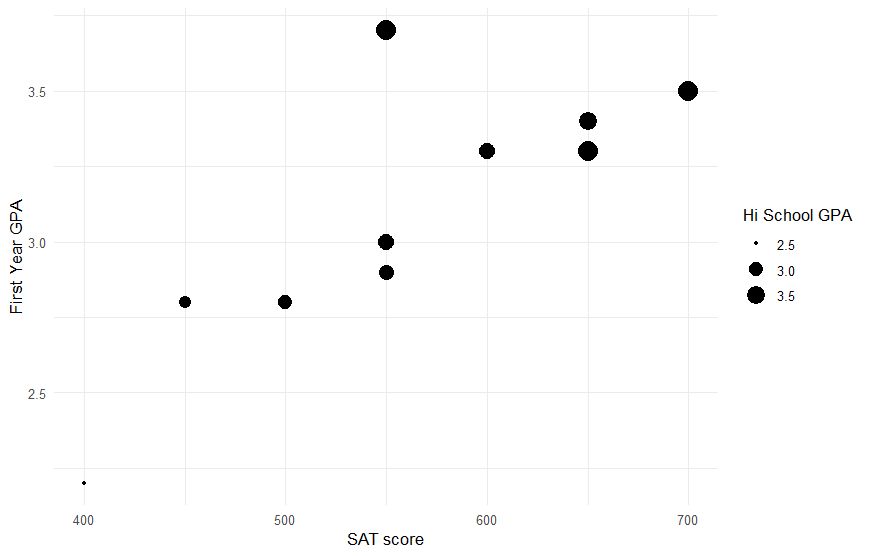
Multiple regression 다중회귀분석
ggplot(scholar) +
aes(x = SATV, y = FGPA, size = HSGPA) +
geom_point() +
scale_color_gradient() +
labs(
y = "First Year GPA",
x = "SAT score",
size = "Hi School GPA"
) +
theme_minimal()
m2 <- lm(FGPA~SATV+HSGPA, data=scholar) summary(m2)
> m2 <- lm(FGPA~SATV+HSGPA, data=scholar)
> summary(m2)
Call:
lm(formula = FGPA ~ SATV + HSGPA, data = scholar)
Residuals:
Min 1Q Median 3Q Max
-0.2431 -0.1125 -0.0286 0.1269 0.2716
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.233102 0.456379 0.51 0.625
SATV 0.000151 0.001405 0.11 0.917
HSGPA 0.845192 0.283816 2.98 0.021 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.192 on 7 degrees of freedom
Multiple R-squared: 0.851, Adjusted R-squared: 0.809
F-statistic: 20.1 on 2 and 7 DF, p-value: 0.00126
>
>
회귀계수 분석 Regression coefficients
아래 회귀식에서 (regression equation) b 값들이 통계학적으로 유의미한지 살펴보는 방법
Y hat (FGPA) = 0.233102 + 0.000151 SATV + 0.845192 HSGPA
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.233102 0.456379 0.51 0.625
SATV 0.000151 0.001405 0.11 0.917
HSGPA 0.845192 0.283816 2.98 0.021 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- 둘 다 양의 상관관계
- 계수값의 단위가 HSGPA가 더 크지만 그 이유는 측정단위 때문에 (FGPA와 HSGPA의 단위가 거의 비슷함 (0 - 4.0)
- 각 변인의 t값을 구하여 significant test를 하여 각각
- t_SATV = 0.11, t_HSGPA = 2.98 을 얻음
- 전자는 Pr(>|t|) 값이 0.917, 후자는 0.021로 HSGPA가 significant하다.
- 각각의 계수를 해석하는 방법은
- SATV를 제외한 독립변인들의 (여기서는 HSGPA 하나) 영향력을 상수화하여 제어했을 때, SATV의 영향력은 SATV의 단위가 하나 증가할 때, 학점은 0.000151 증가하는 것으로 파악된다.
- 마찬가지로 SATV의 영향력을 상수화하여 제어했을 때, FGPA의 단위가 하나 증가하면, 학점은 0.845192 증가한다.
위 분석을 받아들이기 망서리게 되는 이유는 simple regression에서 SATV의 FGPA에 대한 설명력이 유의미하다는 것을 밝혔음에도 불구하고 두개의 독립변인을 동시에 고려할 때에는 중요하지 않은 변인이 되기 때문이다. 이에 대한 설명을 하기 위해서 partial and semipartial correlation 문서를 살펴본다.