sampling_distribution_in_r
Sampling distribution in R e.g. 1
# sampling distribution
n.ajstu <- 100000
mean.ajstu <- 100
sd.ajstu <- 10
set.seed(1024)
ajstu <- rnorm2(n.ajstu, mean=mean.ajstu, sd=sd.ajstu)
mean(ajstu)
sd(ajstu)
var(ajstu)
iter <- 10000 # # of sampling
n.4 <- 4
means4 <- rep (NA, iter)
for(i in 1:iter){
means4[i] = mean(sample(ajstu, n.4))
}
n.25 <- 25
means25 <- rep (NA, iter)
for(i in 1:iter){
means25[i] = mean(sample(ajstu, n.25))
}
n.100 <- 100
means100 <- rep (NA, iter)
for(i in 1:iter){
means100[i] = mean(sample(ajstu, n.100))
}
n.400 <- 400
means400 <- rep (NA, iter)
for(i in 1:iter){
means400[i] = mean(sample(ajstu, n.400))
}
n.900 <- 900
means900 <- rep (NA, iter)
for(i in 1:iter){
means900[i] = mean(sample(ajstu, n.900))
}
n.1600 <- 1600
means1600 <- rep (NA, iter)
for(i in 1:iter){
means1600[i] = mean(sample(ajstu, n.1600))
}
n.2500 <- 2500
means2500 <- rep (NA, iter)
for(i in 1:iter){
means2500[i] = mean(sample(ajstu, n.2500))
}
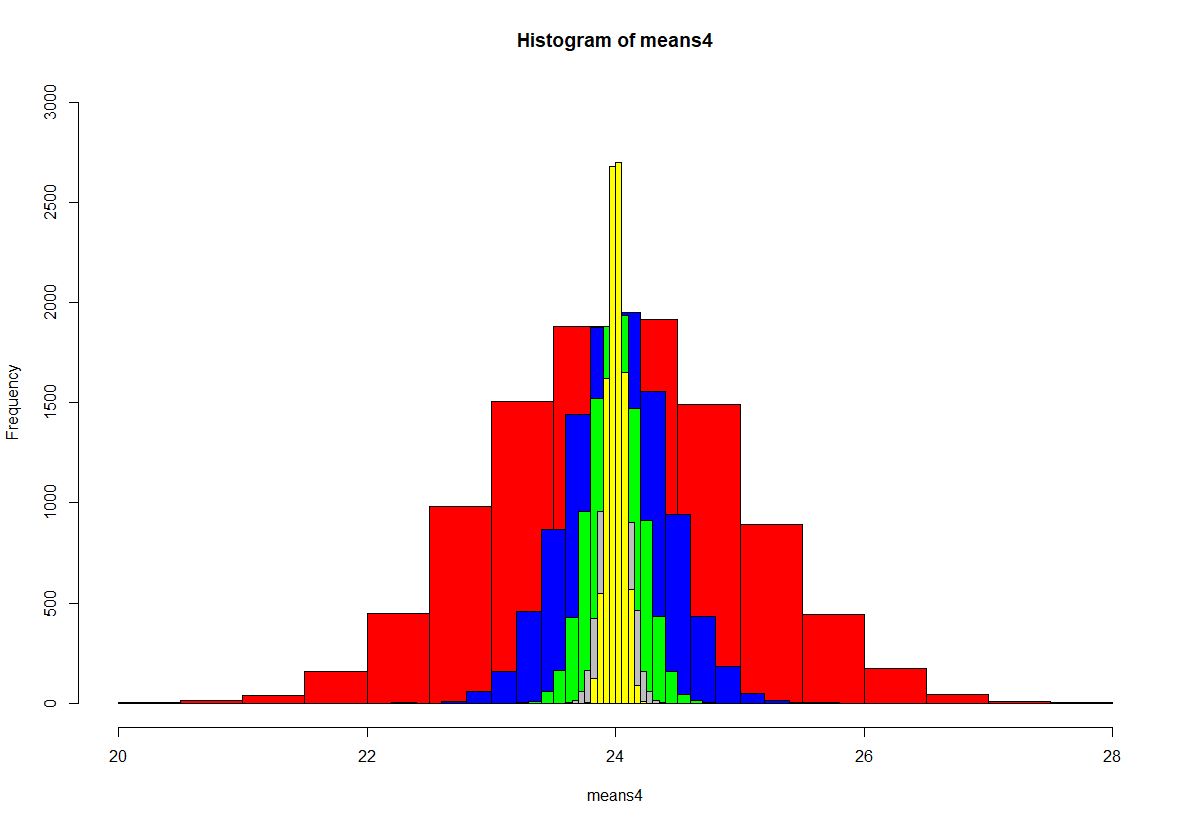
h4 <- hist(means4)
h25 <- hist(means25)
h100 <- hist(means100)
h400 <- hist(means400)
h900 <- hist(means900)
h1600 <- hist(means1600)
h2500 <- hist(means2500)
plot(h4, ylim=c(0,3000), col="red")
plot(h25, add = T, col="blue")
plot(h100, add = T, col="green")
plot(h400, add = T, col="grey")
plot(h900, add = T, col="yellow")
sss <- c(4,25,100,400,900,1600,2500) # sss sample sizes
ses <- rep (NA, length(sss)) # std errors
for(i in 1:length(sss)){
ses[i] = sqrt(var(ajstu)/sss[i])
}
ses.means4 <- sqrt(var(means4))
ses.means25 <- sqrt(var(means25))
ses.means100 <- sqrt(var(means100))
ses.means400 <- sqrt(var(means400))
ses.means900 <- sqrt(var(means900))
ses.means1600 <- sqrt(var(means1600))
ses.means2500 <- sqrt(var(means2500))
ses.real <- c(ses.means4, ses.means25,
ses.means100, ses.means400,
ses.means900, ses.means1600,
ses.means2500)
ses.real
ses
se.1 <- ses
se.2 <- 2 * ses
lower.s2 <- mean(ajstu)-se.2
upper.s2 <- mean(ajstu)+se.2
data.frame(cbind(sss, ses, ses.real, lower.s2, upper.s2))
아웃풋
> n.ajstu <- 100000
> mean.ajstu <- 100
> sd.ajstu <- 10
> set.seed(1024)
> ajstu <- rnorm2(n.ajstu, mean=mean.ajstu, sd=sd.ajstu)
> mean(ajstu)
[1] 100
> sd(ajstu)
[1] 10
> var(ajstu)
[,1]
[1,] 100
> iter <- 10000 # # of sampling
> n.4 <- 4
> means4 <- rep (NA, iter)
> for(i in 1:iter){
+ means4[i] = mean(sample(ajstu, n.4))
+ }
> n.25 <- 25
> means25 <- rep (NA, iter)
> for(i in 1:iter){
+ means25[i] = mean(sample(ajstu, n.25))
+ }
> n.100 <- 100
> means100 <- rep (NA, iter)
> for(i in 1:iter){
+ means100[i] = mean(sample(ajstu, n.100))
+ }
> n.400 <- 400
> means400 <- rep (NA, iter)
> for(i in 1:iter){
+ means400[i] = mean(sample(ajstu, n.400))
+ }
> n.900 <- 900
> means900 <- rep (NA, iter)
> for(i in 1:iter){
+ means900[i] = mean(sample(ajstu, n.900))
+ }
> n.1600 <- 1600
> means1600 <- rep (NA, iter)
> for(i in 1:iter){
+ means1600[i] = mean(sample(ajstu, n.1600))
+ }
> n.2500 <- 2500
> means2500 <- rep (NA, iter)
> for(i in 1:iter){
+ means2500[i] = mean(sample(ajstu, n.2500))
+ }
> h4 <- hist(means4)
> h25 <- hist(means25)
> h100 <- hist(means100)
> h400 <- hist(means400)
> h900 <- hist(means900)
> h1600 <- hist(means1600)
> h2500 <- hist(means2500)
> plot(h4, ylim=c(0,3000), col="red")
> plot(h25, add = T, col="blue")
> plot(h100, add = T, col="green")
> plot(h400, add = T, col="grey")
> plot(h900, add = T, col="yellow")
> sss <- c(4,25,100,400,900,1600,2500) # sss sample sizes
> ses <- rep (NA, length(sss)) # std errors
> for(i in 1:length(sss)){
+ ses[i] = sqrt(var(ajstu)/sss[i])
+ }
> ses
[1] 5.0000000 2.0000000 1.0000000 0.5000000 0.3333333 0.2500000
[7] 0.2000000
> se.1 <- ses
> se.2 <- 2 * ses
> lower.s2 <- mean(ajstu)-se.2
> upper.s2 <- mean(ajstu)+se.2
> data.frame(cbind(sss, ses, lower.s2, upper.s2))
sss ses lower.s2 upper.s2
1 4 5.0000000 90.00000 110.0000
2 25 2.0000000 96.00000 104.0000
3 100 1.0000000 98.00000 102.0000
4 400 0.5000000 99.00000 101.0000
5 900 0.3333333 99.33333 100.6667
6 1600 0.2500000 99.50000 100.5000
7 2500 0.2000000 99.60000 100.4000
> sss <- c(4,25,100,400,900,1600,2500) # sss sample sizes
> ses <- rep (NA, length(sss)) # std errors
> for(i in 1:length(sss)){
+ ses[i] = sqrt(var(ajstu)/sss[i])
+ }
> ses.means4 <- sqrt(var(means4))
> ses.means25 <- sqrt(var(means25))
> ses.means100 <- sqrt(var(means100))
> ses.means400 <- sqrt(var(means400))
> ses.means900 <- sqrt(var(means900))
> ses.means1600 <- sqrt(var(means1600))
> ses.means2500 <- sqrt(var(means2500))
> ses.real <- c(ses.means4, ses.means25,
+ ses.means100, ses.means400,
+ ses.means900, ses.means1600,
+ ses.means2500)
> ses.real
[1] 4.9719142 2.0155741 0.9999527 0.5034433 0.3324414 0.2466634
[7] 0.1965940
> ses
[1] 5.0000000 2.0000000 1.0000000 0.5000000 0.3333333 0.2500000
[7] 0.2000000
> se.1 <- ses
> se.2 <- 2 * ses
> lower.s2 <- mean(ajstu)-se.2
> upper.s2 <- mean(ajstu)+se.2
> data.frame(cbind(sss, ses, ses.real, lower.s2, upper.s2))
sss ses ses.real lower.s2 upper.s2
1 4 5.0000000 4.9719142 90.00000 110.0000
2 25 2.0000000 2.0155741 96.00000 104.0000
3 100 1.0000000 0.9999527 98.00000 102.0000
4 400 0.5000000 0.5034433 99.00000 101.0000
5 900 0.3333333 0.3324414 99.33333 100.6667
6 1600 0.2500000 0.2466634 99.50000 100.5000
7 2500 0.2000000 0.1965940 99.60000 100.4000
>
# n =1600 일 경우에 # sample의 평균이 100.15보다 작을 # 확률은 어떻게 구해야 할까? # n = 1600 일 경우에 # sampling distribution은 # Xbar ~ N(100, var(ajstu)/n.1600) # 그리고, 위에서 standard error값은 # sqrt(var(ajstu)/n.1600) # 이것을 standard error라고 부른다 # 따라서 se.1600 <- sqrt(var(ajstu)/n.1600) pnorm(100.15, mean(ajstu), se.1600)
Sampling distribution in proportion in R
pop <- rbinom(100000, size = 1, prob = 0.5)
par(mfrow=c(2,2))
iter <- 10000
n <- 5
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
hist(means, xlim=c(0,1), main=n)
iter <- 10000
n <- 25
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
hist(means, xlim=c(0,1), main=n)
iter <- 10000
n <- 100
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
hist(means, xlim=c(0,1), main=n)
iter <- 10000
n <- 900
means <- rep (NA, iter)
for(i in 1:iter){
means[i] = mean(sample(pop, n))
}
mean(means)
sd(means)
var(means)
hist(means, xlim=c(0,1), main=n)
par(mfrow=c(1,1))
set.seed(2020)
pop <- rbinom(100000, size = 1, prob = 0.4)
par(mfrow=c(2,2))
iter <- 1000
ns <- c(25, 100, 400, 900)
l.ns <- length(ns)
for (i in 1:l.ns) {
for(k in 1:iter) {
means[k] = mean(sample(pop, ns[i]))
}
mean(means)
sd(means)
hist(means, xlim=c(0,1), main=n)
}
par(mfrow=c(1,1))
0.5가 비율인 (proportion) 모집단에 대한 여론 조사를 위해서 900명의 샘플을 취하고 이를 이용하여 모집단의 위치를 추정하자.
n <- 900 samp <- sample(pop, n) mean(samp) p <- mean(samp) q <- 1-p ser <- sqrt((p*q)/n) ser2 <- ser * 2 p - ser2 p + ser2
sampling_distribution_in_r.txt · Last modified: by hkimscil