Table of Contents
SNA (Social Network Analysis)
Read: Social network analysis - theory and application
참조: Introduction to social network methods
SA, introduction to sna in Models for Social Networks With Statistical Applications (Advanced Quantitative Techniques in the Social Sciences series) 1412941687
Crime and Social Network Analysis
Studies of attributes
social studies of people . . . studies of attributes of people = attribute studies
| Gender | Race | Height | Income | Marital Status | Years of Educ | Liberal- ness |
|
|---|---|---|---|---|---|---|---|
| p0001 | M | 1 | 170 | 5000 | 1 | 12 | 1.73 |
| p0002 | M | 2 | 183 | 10000 | 1 | 20 | 4.53 |
| p0003 | F | 1 | 160 | 2500 | 1 | 16 | 2.99 |
| p0004 | M | 2 | 175 | 3000 | 2 | 16 | 1.13 |
| p0005 | F | 1 | 159 | 3500 | 3 | 12 | 3.81 |
| p0006 | M | 1 | 186 | 4500 | 1 | 9 | 4.76 |
| p0007 | F | 5 | 162 | 5000 | 2 | 21 | 2.01 |
| p0008 | F | 4 | 154 | 1200 | 1 | 18 | 1.27 |
| p0009 | M | 1 | 172 | 5300 | 1 | 12 | 3.25 |
- Difference between male/female = difference between variable gender about something…
- 특성(attributes) 데이터는 인간행위자의 태도, 의견, 행위 (attitudes, opinions, behavior) 등에 관한 데이터라고 할 수 있는데, 이들 대부분의 것들은 대답을 한 행위자의 특성으로 여겨지게 된다. 이 특성은 IV와 DV로 작용을 하여 어떤 것이 어떤 것에 영향을 주는 식으로 추정(inference)되는 것이 보통이다. 가령, 여성/남성으로 이루어진 젠더라는 특성은 인간의 수학적 능력(mathematical ability)에 영향을 줄 것이라는 추정이다. 연구자는 이런 추정을 토대로 사람들에게서 젠더라는 특성과 수학적 능력이라는 특성을 추출(survey 혹은 experiment를 통해서)해 내게된다. 이 때, 관심을 가진 모든 사람들의 (모집단, population) 특성을 추출해 낼 수 없으므로, 샘플링 작업을 통하여 이를 대표할 수 있는 (representative) 집단을 추출하여, 그 특성의 특징과 (statistics) 특성 간의 관계를 살펴본 후 (inferential statistics), 이를 통해서 모집단의 성격을 추정하게 된다 (parameter). 이런 모집단의 특성을 추정하기 위해서 사용되는 통계학적 개념 중 가장 많이 사용되는 것이 표준오차(standard error)와 같은 개념이다.
- standard error . . .
- 이 때 남자이기 때문에 특정한 생각이나 태도가 형성된다라고 주장하는 것에는 생물학적 + 사회학적인 영향력이 그 사람의 생각/태도를 지배(영향력을 줌) 한다라는 가정이 깔려 있는 셈이다. 즉, 남자라는 카테고리, 사회경제적지위가 높은 사람, 학력 (초, 중, 고, 대학교, 대학교이상, 졸업) 이라는 카테고리의 사회학적인 역할이 가정되는 것이다. 이런 카테고리가 획일적인 결과를 초래하지는 않기에 (만약에 그렇다면 인간학(사회학)은 물리학과 같은 류의 학문이 될 것이다) 그 차이점에서 발현될 것이라고 생각하는 (이론이나 상식을 바탕으로 한 추론에 근거한 의견 = 가설) 결과를 통계치를 통해서 살펴보는 것이다.
- 위에서 특징으로 인해서 발현되는 그 무엇이 사회의 일반성에 (regularity) 영향을 준다고 할 수 있는데, 연구자는 “관계” 또한 인간의 태도나 의견, 행동과 관련이 있다는 주장을 할 수도 있다. 즉, 남자라는 사회학적인 특성은 사회학적으로 특정한 결과를 (태도, 의견, 행동) 초래하도록 하는것 처럼, 어떤 사회적 그룹에서, 특정한 사람들과 관계를 맺는다는 것이, 그들만의 태도, 의견, 행동의 패턴을 굳히도록 하는 것이라고 주장할 수도 있는 것이다. 바로 이 “사회적 그룹에서의 사람들 간의 관계”를 social network data라고 하고, 이를 분석하는 것을 social network data analysis라고 한다.
일반적으로 SNA는 아래의 것들을 강조한다.
- focus on relationships between actors rather than attributes of actors
- sense of interdependence: a molecular rather atomistic view
- structure affects substantive outcomes
- emergent effects
E.g.,
또 다른 approach로 아래를 생각해 볼 수 있다. 아래는 미국 주요 도시 간의 거리를 나타내는 테이블 형식의 데이터이다. 역기서 중요한 것은 각 도시 간의 거리를 알고있다면 (정확하다고 하면), 연구자는 도시들 간의 거리만을 표시함으로써 실제 지형의 맵을 완성할 수 있다는 것이다.
| Cities | Boston | Chicago | Denver | LosAngeles | New York | San Francisco | Seattle | Washington |
|---|---|---|---|---|---|---|---|---|
| Boston, Mass. | - | 851 | 1769 | 2596 | 188 | 2699 | 2493 | 393 |
| Chicago, Ill. | 851 | - | 920 | 1745 | 713 | 1858 | 1737 | 597 |
| Denver, Colo. | 1769 | 920 | - | 831 | 1631 | 949 | 1021 | 1494 |
| Los Angeles, Calif. | 2596 | 1745 | 831 | - | 2451 | 347 | 959 | 2300 |
| New York, N.Y. | 188 | 713 | 1631 | 2451 | - | 2571 | 2408 | 205 |
| San Francisco, Calif. | 2699 | 1858 | 949 | 347 | 2571 | - | 678 | 2442 |
| Seattle, Wash. | 2493 | 1737 | 1021 | 959 | 2408 | 678 | - | 2329 |
| Washington, D.C. | 393 | 597 | 1494 | 2300 | 205 | 2442 | 2329 | - |
아래는 위의 데이터에 기반하여 만든 맵이다. 이 맵은 이제, 실제 지도와 흡사한 모양을 가지게 된다.
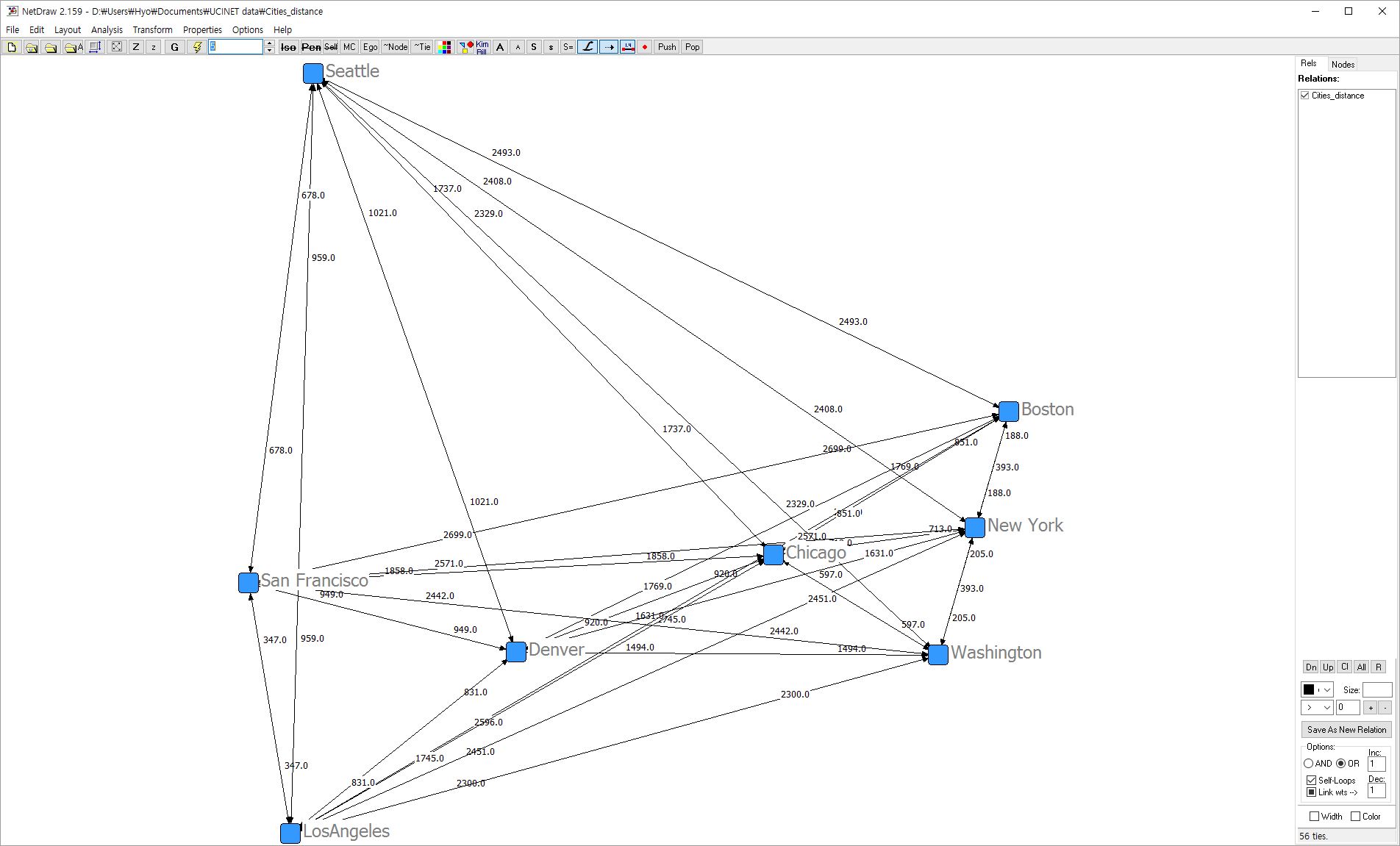
이를 사람의 관계에 적용한다고 가정하면, 그리고 그 관계의 거리를 정확하게 측정할 수 있는 방법만 있다면, 그 사회의 사회적인 맵을 완성할 수도 있다고 결론지을 수도 있다. 이것이 관계의 그래프이론이다. 그리고, 이런 류의 이론은 측정(metric)을 중요시하고 이를 위해서 많은 노력을 기울인다 1).
이런 관계의 측정을 연구하면서 사회관계망 연구자들의 사람들 간의 수치화된 관계 외에 관계의 있고/없음을 (binary) 기록한 데이터로서 그 사회의 일 단면을 살펴보는 단서가 된다고 발전시켰다. 또한 이에 더 나아가, 사건이나 상황에 대한 참여(participation), 관여(involvement), 등 또한 관계망 연구에 활용이 된다고 하였다.
Examples
- Who reports whom?
- Who likes whom (in a class)?
- Getting a job: Strength of weak ties
- Performance: Structural hole
- Cohesion vs. Structural equivalence
- Diffusion: Diffusion of Innovation
- Diffusion Theory by Eve Rogers
- Deroı̈an, Frédéric (2002). Formation of social networks and diffusion of innovations
Concepts
Terms
- nodes, actors, points: 보통 사람이나 사회적 주체를 의미한다.
- edges, relationships, lines: 라인으로 표현되는데, 관계의 유무 혹은 정도를 의미한다.
Study of (see Measures in social network analysis)
- nodes (edges)
- absence (or presence) of intimate edges within a society
- Korea vs. Norway
- the characteristics of edges ::
- the strength of weak ties
- Multiple relations
- report network + friendship network » organizational group performance ??
- actors (position, cohesion, etc)
- Structural hole
- Structural equivalence
- Structural cohesion
-
- betweenness
- closeness
- degree
- centality
- bridge
- etc.
- network itself
- centralization
- the above characteristics in comparison to larger networks (organizations in a country, for example)
- parties
- networks (between or among networks)
- CONCOR (convergence of Correlations?)
- . . . .
Node measurements
- binary = nominal (absence/presence)
- ordinary
- interval/ratio
Nodes . . . what could they be?
- Ego network 참조 … Egos can be persons, groups, organizations, or whole societies. . . .
- 연결의 유무, 방향, 정도 등을 일반화하여 개인의 역할, 지위, 등을 매핑해 볼 수 있다. 가장 간단한 예가 centrality이다.
- degree
- closeness
- betweenness
- etc. . . .
Who is more influential in this type of social relationship arrangement?
- How many lines does each have? A vs. . .
- How close is one to every other?
- Betweenness
E.g.2
Matrix calculation
see How to Multiply Matrices at maths is fun site.
In R . . . .
matrix (c(1,1,1,2…)), byrow=T, nrow=36, ncol=2)
이 의미하는 것은 ncol=2 이므로
1,1
1,2
1,3
과 같은 데이터형식을 같는다는 것(nrow와 ncol에 의해서)과
1과1, 1과2 등은 관계가 있음을 나타내 주는 것이다.
classtaken = matrix(0,8,10)
# 0으로 채워진 8 x 10 크기의 matrix 만들기
# 8 students
# 10 classes
classtaken
edge.list = matrix (
c(1,1,1,2,1,3,1,4,1,9,
2,2,2,5,2,7,2,8,
3,1,3,5,3,6,3,7,3,8,
4,2,4,6,4,9,4,10,
5,1,5,2,5,5,5,7,5,8,
6,2,6,3,6,4,6,7,
7,3,7,4,7,7,7,8,
8,1,8,2,8,6,8,9,8,10), byrow=T, nrow=36,ncol=2)
# 둘로 짝지어진 (ncol = 2) 관계 위치를 edge.list에 기록하기
# (1,1)은 매트릭스의 row 1, column 1 위치를 의미
classtaken[edge.list] = 1
# 0으로만 채워졌던 classtaken matrix에 [edge.list]자리는 0을 1로 바꾸기
# 위에서 언급된 위치에 1을 주기
classtaken # classtaken 데이터 확인
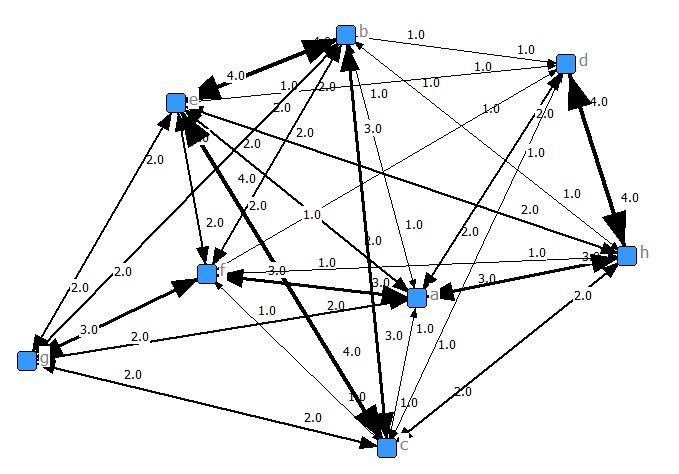
rownames(classtaken) = c("a","b", "c", "d","e", "f", "g", "h")
colnames(classtaken) = c("writer", "comtheo", "pr","adv",
"broadc","internet","camshoot", "edit",
"newmedia", "cmc")
classtaken
c = classtaken
tc = t(classtaken)
stu = c %*% tc
class = tc %*% c
stu
class
| Two mode matrix (students x classes taken) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | writer | comTheo | pr | adv | broadc | internet | camShoot | edit | newMedia | CMC |
| a | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| b | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| c | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| d | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| e | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| f | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| g | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| h | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
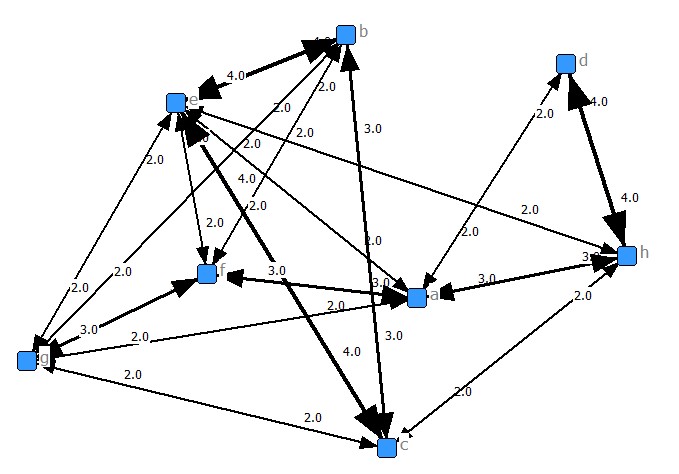
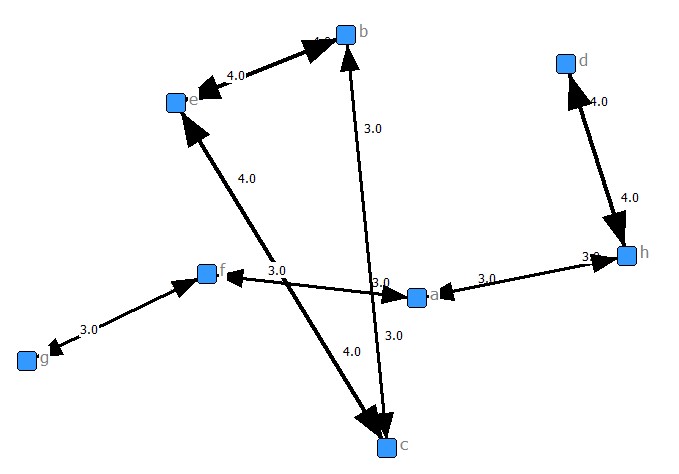
| One mode matrix (students x students) | ||||||||
|---|---|---|---|---|---|---|---|---|
| ID | a | b | c | d | e | f | g | h |
| a | 5 | 1 | 1 | 2 | 2 | 3 | 2 | 3 |
| b | 1 | 4 | 3 | 1 | 4 | 2 | 2 | 1 |
| c | 1 | 3 | 5 | 1 | 4 | 1 | 2 | 2 |
| d | 2 | 1 | 1 | 4 | 1 | 1 | 0 | 4 |
| e | 2 | 4 | 4 | 1 | 5 | 2 | 2 | 2 |
| f | 3 | 2 | 1 | 1 | 2 | 4 | 3 | 1 |
| g | 2 | 2 | 2 | 0 | 2 | 3 | 4 | 0 |
| h | 3 | 1 | 2 | 4 | 2 | 1 | 0 | 5 |
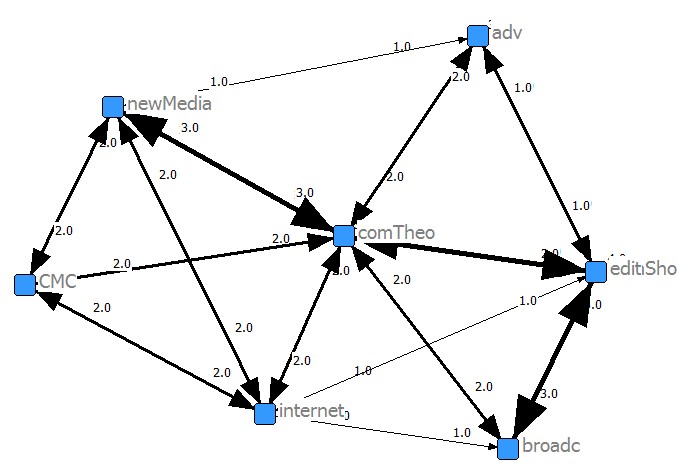
| One mode matrix (classes x classes) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | writer | comTheo | pr | adv | broadc | internet | camShoot | edit | newMedia | CMC |
| writer | 4 | 3 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 1 |
| comTheo | 3 | 6 | 2 | 2 | 2 | 2 | 3 | 2 | 3 | 2 |
| pr | 1 | 2 | 3 | 3 | 0 | 0 | 2 | 1 | 1 | 0 |
| adv | 1 | 2 | 3 | 3 | 0 | 0 | 2 | 1 | 1 | 0 |
| broadc | 2 | 2 | 0 | 0 | 3 | 1 | 3 | 3 | 0 | 0 |
| internet | 2 | 2 | 0 | 0 | 1 | 3 | 1 | 1 | 2 | 2 |
| camShoot | 2 | 3 | 2 | 2 | 3 | 1 | 5 | 4 | 0 | 0 |
| edit | 2 | 2 | 1 | 1 | 3 | 1 | 4 | 4 | 0 | 0 |
| newMedia | 2 | 3 | 1 | 1 | 0 | 2 | 0 | 0 | 3 | 2 |
| CMC | 1 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 2 |
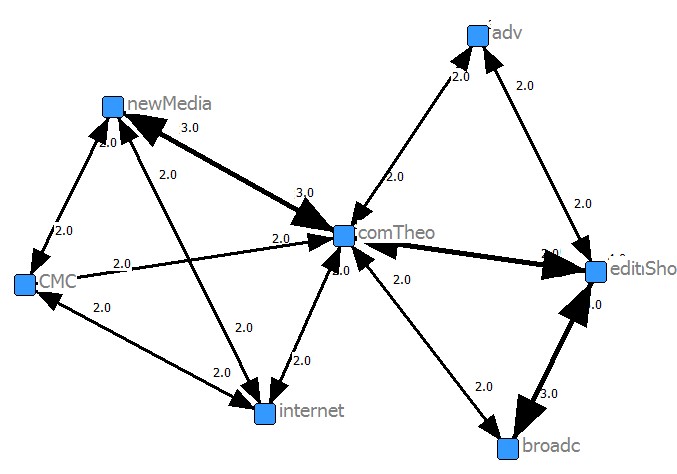
Suppose that this is web sites (nodes composed with links)
| ID | writer | comTheo | pr | adv | broadc | internet | camShoot | edit | newMedia | CMC |
|---|---|---|---|---|---|---|---|---|---|---|
| writer | 4 | 3 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 1 |
| comTheo | 3 | 6 | 2 | 2 | 2 | 2 | 3 | 2 | 3 | 2 |
| pr | 1 | 2 | 3 | 3 | 0 | 0 | 2 | 1 | 1 | 0 |
| adv | 1 | 2 | 3 | 3 | 0 | 0 | 2 | 1 | 1 | 0 |
| broadc | 2 | 2 | 0 | 0 | 3 | 1 | 3 | 3 | 0 | 0 |
| internet | 2 | 2 | 0 | 0 | 1 | 3 | 1 | 1 | 2 | 2 |
| camShoot | 2 | 3 | 2 | 2 | 3 | 1 | 5 | 4 | 0 | 0 |
| edit | 2 | 2 | 1 | 1 | 3 | 1 | 4 | 4 | 0 | 0 |
| newMedia | 2 | 3 | 1 | 1 | 0 | 2 | 0 | 0 | 3 | 2 |
| CMC | 1 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 2 |
위와 같은 이원데이터 (binary matrix 혹은 two-mode matrix data)는 여러 다른 곳에서도 활용될 수 있다는 점이다. 사실, IT의 역사에 남을 Google 또한 이 방법을 이용하여 search engine으로서의 위상을 높혔다. 이 외에도 아래의 예가 있다.
- Google의 page rank
- Amazon.com의 책추천
- Pandora.com의 노래추천
- citation analysis 등등
E.g.3. CONCOR
please refer to https://www.r-bloggers.com/concor-in-r/
also note:
- RDGAM, participation in horseplay;
- RDCON, participation in arguments about open windows;
- RDPOS, friendship;
- RDNEG, antagonistic (negative) behavior;
- RDHLP, helping others with work; and
- RDJOB, the number of times workers traded job assignments.
#REPLICATE BREIGER ET AL. (1975)
#INSTALL CONCOR
install.packages("devtools")
devtools::install_github("aslez/concoR")
#LIBRARIES
library(concoR)
library(sna)
#LOAD DATA
data(bank_wiring)
bank_wiring
#CHECK INITIAL CORRELATIONS (TABLE III)
m0 <- cor(do.call(rbind, bank_wiring))
round(m0, 2)
#IDENTIFY BLOCKS USING A 4-BLOCK MODEL (TABLE IV)
blks <- concor_hca(bank_wiring, p = 2)
blks
#CHECK FIT USING SNA (TABLE V)
#code below fails unless glabels are specified
blk_mod <- blockmodel(bank_wiring, blks$block,
glabels = names(bank_wiring),
plabels = rownames(bank_wiring[[1]]))
blk_mod
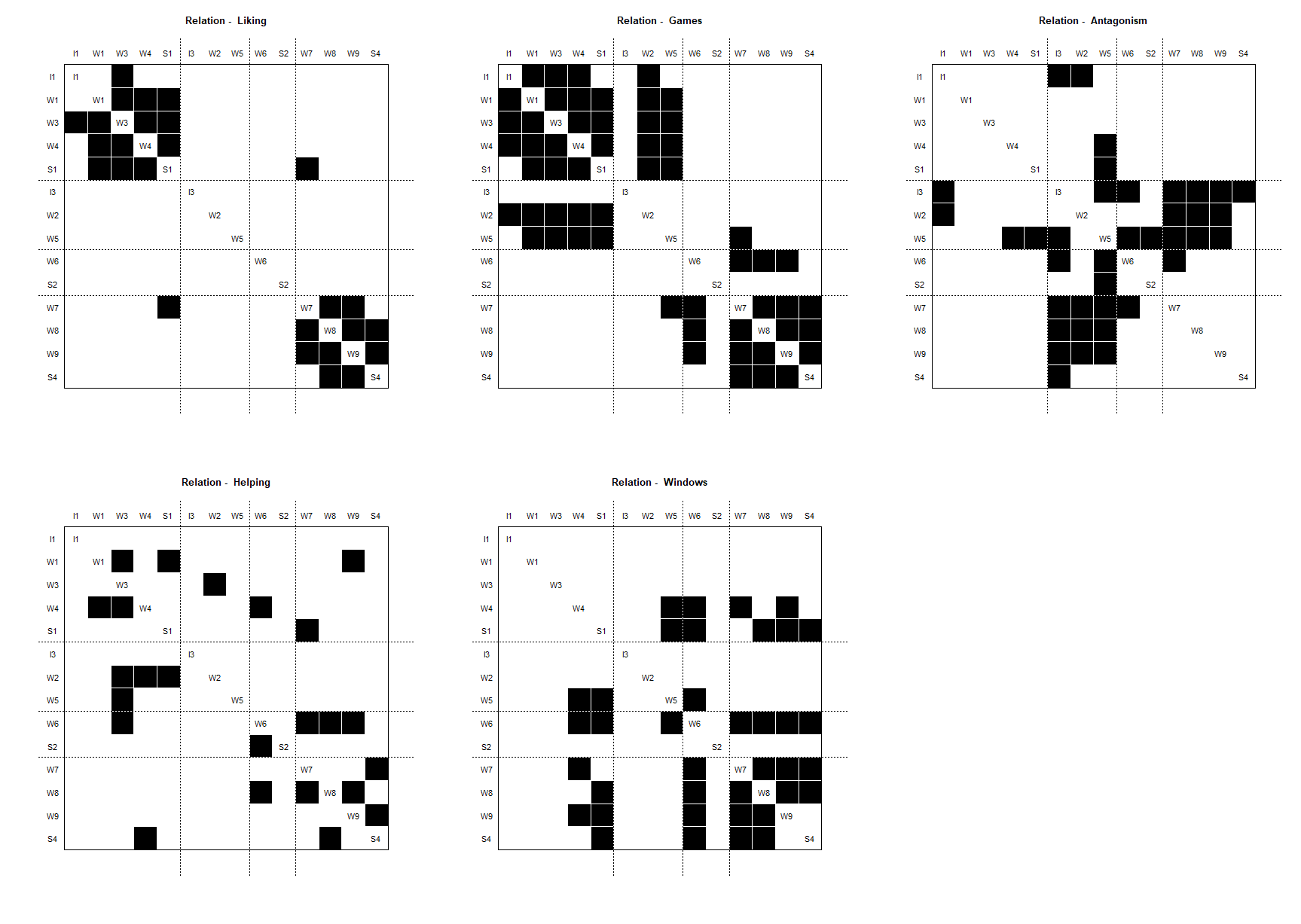
plot(blk_mod)
> #REPLICATE BREIGER ET AL. (1975)
> #INSTALL CONCOR
> devtools::install_github("aslez/concoR")
Skipping install of 'concoR' from a github remote, the SHA1 (618d8be5) has not changed since last install.
Use `force = TRUE` to force installation
>
> #LIBRARIES
> library(concoR)
> library(sna)
>
> #LOAD DATA
> data(bank_wiring)
> bank_wiring
$Liking
I1 I3 W1 W2 W3 W4 W5 W6 W7 W8 W9 S1 S2 S4
I1 0 0 0 0 1 0 0 0 0 0 0 0 0 0
I3 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W1 0 0 0 0 1 1 0 0 0 0 0 1 0 0
W2 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W3 1 0 1 0 0 1 0 0 0 0 0 1 0 0
W4 0 0 1 0 1 0 0 0 0 0 0 1 0 0
W5 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W6 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W7 0 0 0 0 0 0 0 0 0 1 1 1 0 0
W8 0 0 0 0 0 0 0 0 1 0 1 0 0 1
W9 0 0 0 0 0 0 0 0 1 1 0 0 0 1
S1 0 0 1 0 1 1 0 0 1 0 0 0 0 0
S2 0 0 0 0 0 0 0 0 0 0 0 0 0 0
S4 0 0 0 0 0 0 0 0 0 1 1 0 0 0
$Games
I1 I3 W1 W2 W3 W4 W5 W6 W7 W8 W9 S1 S2 S4
I1 0 0 1 1 1 1 0 0 0 0 0 0 0 0
I3 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W1 1 0 0 1 1 1 1 0 0 0 0 1 0 0
W2 1 0 1 0 1 1 0 0 0 0 0 1 0 0
W3 1 0 1 1 0 1 1 0 0 0 0 1 0 0
W4 1 0 1 1 1 0 1 0 0 0 0 1 0 0
W5 0 0 1 0 1 1 0 0 1 0 0 1 0 0
W6 0 0 0 0 0 0 0 0 1 1 1 0 0 0
W7 0 0 0 0 0 0 1 1 0 1 1 0 0 1
W8 0 0 0 0 0 0 0 1 1 0 1 0 0 1
W9 0 0 0 0 0 0 0 1 1 1 0 0 0 1
S1 0 0 1 1 1 1 1 0 0 0 0 0 0 0
S2 0 0 0 0 0 0 0 0 0 0 0 0 0 0
S4 0 0 0 0 0 0 0 0 1 1 1 0 0 0
$Antagonism
I1 I3 W1 W2 W3 W4 W5 W6 W7 W8 W9 S1 S2 S4
I1 0 1 0 1 0 0 0 0 0 0 0 0 0 0
I3 1 0 0 0 0 0 1 1 1 1 1 0 0 1
W1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W2 1 0 0 0 0 0 0 0 1 1 1 0 0 0
W3 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W4 0 0 0 0 0 0 1 0 0 0 0 0 0 0
W5 0 1 0 0 0 1 0 1 1 1 1 1 1 0
W6 0 1 0 0 0 0 1 0 1 0 0 0 0 0
W7 0 1 0 1 0 0 1 1 0 0 0 0 0 0
W8 0 1 0 1 0 0 1 0 0 0 0 0 0 0
W9 0 1 0 1 0 0 1 0 0 0 0 0 0 0
S1 0 0 0 0 0 0 1 0 0 0 0 0 0 0
S2 0 0 0 0 0 0 1 0 0 0 0 0 0 0
S4 0 1 0 0 0 0 0 0 0 0 0 0 0 0
$Helping
I1 I3 W1 W2 W3 W4 W5 W6 W7 W8 W9 S1 S2 S4
I1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
I3 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W1 0 0 0 0 1 0 0 0 0 0 1 1 0 0
W2 0 0 0 0 1 1 0 0 0 0 0 1 0 0
W3 0 0 0 1 0 0 0 0 0 0 0 0 0 0
W4 0 0 1 0 1 0 0 1 0 0 0 0 0 0
W5 0 0 0 0 1 0 0 0 0 0 0 0 0 0
W6 0 0 0 0 1 0 0 0 1 1 1 0 0 0
W7 0 0 0 0 0 0 0 0 0 0 0 0 0 1
W8 0 0 0 0 0 0 0 1 1 0 1 0 0 0
W9 0 0 0 0 0 0 0 0 0 0 0 0 0 1
S1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
S2 0 0 0 0 0 0 0 1 0 0 0 0 0 0
S4 0 0 0 0 0 1 0 0 0 1 0 0 0 0
$Windows
I1 I3 W1 W2 W3 W4 W5 W6 W7 W8 W9 S1 S2 S4
I1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
I3 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W2 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W3 0 0 0 0 0 0 0 0 0 0 0 0 0 0
W4 0 0 0 0 0 0 1 1 1 0 1 0 0 0
W5 0 0 0 0 0 1 0 1 0 0 0 1 0 0
W6 0 0 0 0 0 1 1 0 1 1 1 1 0 1
W7 0 0 0 0 0 1 0 1 0 1 1 0 0 1
W8 0 0 0 0 0 0 0 1 1 0 1 1 0 1
W9 0 0 0 0 0 1 0 1 1 1 0 1 0 0
S1 0 0 0 0 0 0 1 1 0 1 1 0 0 1
S2 0 0 0 0 0 0 0 0 0 0 0 0 0 0
S4 0 0 0 0 0 0 0 1 1 1 0 1 0 0
>
> #CHECK INITIAL CORRELATIONS (TABLE III)
> m0 <- cor(do.call(rbind, bank_wiring))
> round(m0, 2)
I1 I3 W1 W2 W3 W4 W5 W6 W7 W8 W9 S1 S2 S4
I1 1.00 -0.11 0.41 0.27 0.17 0.27 0.27 -0.07 0.00 0.03 0.02 0.37 -0.04 -0.03
I3 -0.11 1.00 -0.14 0.41 -0.17 -0.07 0.27 0.05 0.00 -0.08 -0.09 -0.08 0.36 -0.15
W1 0.41 -0.14 1.00 0.30 0.58 0.46 0.07 -0.12 -0.08 -0.23 -0.24 0.34 -0.05 -0.19
W2 0.27 0.41 0.30 1.00 0.18 0.17 0.46 -0.12 -0.26 -0.23 -0.24 0.05 -0.05 -0.19
W3 0.17 -0.17 0.58 0.18 1.00 0.38 -0.04 -0.20 -0.10 -0.21 -0.15 0.35 -0.06 -0.24
W4 0.27 -0.07 0.46 0.17 0.38 1.00 0.03 0.03 0.03 0.09 -0.09 0.56 0.22 -0.07
W5 0.27 0.27 0.07 0.46 -0.04 0.03 1.00 0.11 -0.04 0.01 0.07 0.01 -0.07 0.11
W6 -0.07 0.05 -0.12 -0.12 -0.20 0.03 0.11 1.00 0.33 0.33 0.38 0.09 0.22 0.38
W7 0.00 0.00 -0.08 -0.26 -0.10 0.03 -0.04 0.33 1.00 0.45 0.50 0.08 0.19 0.30
W8 0.03 -0.08 -0.23 -0.23 -0.21 0.09 0.01 0.33 0.45 1.00 0.58 0.07 0.21 0.36
W9 0.02 -0.09 -0.24 -0.24 -0.15 -0.09 0.07 0.38 0.50 0.58 1.00 0.05 0.20 0.43
S1 0.37 -0.08 0.34 0.05 0.35 0.56 0.01 0.09 0.08 0.07 0.05 1.00 0.21 -0.08
S2 -0.04 0.36 -0.05 -0.05 -0.06 0.22 -0.07 0.22 0.19 0.21 0.20 0.21 1.00 -0.05
S4 -0.03 -0.15 -0.19 -0.19 -0.24 -0.07 0.11 0.38 0.30 0.36 0.43 -0.08 -0.05 1.00
>
> #IDENTIFY BLOCKS USING A 4-BLOCK MODEL (TABLE IV)
> blks <- concor_hca(bank_wiring, p = 2)
> blks
block vertex
1 1 I1
6 2 I3
2 1 W1
7 2 W2
3 1 W3
4 1 W4
8 2 W5
9 3 W6
11 4 W7
12 4 W8
13 4 W9
5 1 S1
10 3 S2
14 4 S4
>
> #CHECK FIT USING SNA (TABLE V)
> #code below fails unless glabels are specified
> blk_mod <- blockmodel(bank_wiring, blks$block,
+ glabels = names(bank_wiring),
+ plabels = rownames(bank_wiring[[1]]))
> blk_mod
Network Blockmodel:
Block membership:
I1 I3 W1 W2 W3 W4 W5 W6 W7 W8 W9 S1 S2 S4
1 2 1 2 1 1 2 3 4 4 4 1 3 4
Reduced form blockmodel:
Liking
Block 1 Block 2 Block 3 Block 4
Block 1 0.70 0 0 0.0500000
Block 2 0.00 0 0 0.0000000
Block 3 0.00 0 0 0.0000000
Block 4 0.05 0 0 0.8333333
Games
Block 1 Block 2 Block 3 Block 4
Block 1 0.9 0.60000000 0.000 0.00000000
Block 2 0.6 0.00000000 0.000 0.08333333
Block 3 0.0 0.00000000 0.000 0.37500000
Block 4 0.0 0.08333333 0.375 1.00000000
Antagonism
Block 1 Block 2 Block 3 Block 4
Block 1 0.0000000 0.2666667 0.000 0.0000000
Block 2 0.2666667 0.3333333 0.500 0.8333333
Block 3 0.0000000 0.5000000 0.000 0.1250000
Block 4 0.0000000 0.8333333 0.125 0.0000000
Helping
Block 1 Block 2 Block 3 Block 4
Block 1 0.2000000 0.06666667 0.100 0.1000000
Block 2 0.2666667 0.00000000 0.000 0.0000000
Block 3 0.1000000 0.00000000 0.500 0.3750000
Block 4 0.0500000 0.00000000 0.125 0.4166667
Windows
Block 1 Block 2 Block 3 Block 4
Block 1 0.0000000 0.1333333 0.2000000 0.2500000
Block 2 0.1333333 0.0000000 0.1666667 0.0000000
Block 3 0.2000000 0.1666667 0.0000000 0.5000000
Block 4 0.2500000 0.0000000 0.5000000 0.8333333
> plot(blk_mod)
>
Readings
- 김용학 2004. 사회연결망이론(개정판). 박영사.
- 김용학. 2003. 사회연결망분석. 박영사.
- Wasserman, Stanley and Katherine Faust. 1994. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.
- Knoke, David and James H. Kuklinski. 1982. Network Analysis. Beverly Hills, California: SAGE Publications.
- Scott, John. 1991. Social Network Analysis: a handbook. Newbury Park, California: SAGE Publications.
- Wellman, Barry and Berkowitz S.D. 1988. Social Structures: A Network Approach. Cambridge: Cambridge University Press.
- Degenne, Alain and Michel Forse. 1999. Introducing Social Networks. London: SAGE Publications
Introductions to sna
- Borgatti, S.P et al (2009). Network Analysis in the Social Sciences Science 323-892. PDF
- Butts, Carter T. (2009). Revisiting the Foundations of Network Analysis. Science. 325-414. PDF file
- Emirbayer, M. 1997. Manifesto for Relational Sociology. American Journal of Sociology 103. 281-317.
Org. and sites
Tools and applications
Draft
- see https://rpubs.com/pjmurphy/539996 for detail
PADGETT FLORENTINE FAMILIES
DATASET PADGETT and PADGW / Pajek
DESCRIPTION PADGETT
Two 16×16 matrices:
PADGB symmetric binary
PADGM symmetric binary
PADGW
One 16×3 matrix, valued.
BACKGROUND Breiger & Pattison (1986), in their discussion of local role analysis, use a subset of data on the social relations among Renaissance Florentine families (person aggregates) collected by John Padgett from historical documents. The two relations are business ties (PADGB - specifically, recorded financial ties such as loans, credits and joint partnerships) and marriage alliances (PADGM).
As Breiger & Pattison point out, the original data are symmetrically coded. This is acceptable perhaps for marital ties, but is unfortunate for the financial ties (which are almost certainly directed). To remedy this, the financial ties can be recoded as directed relations using some external measure of power - for instance, a measure of wealth. PADGW provides information on (1) each family's net wealth in 1427 (in thousands of lira); (2) the number of priorates (seats on the civic council) held between 1282- 1344; and (3) the total number of business or marriage ties in the total dataset of 116 families (see Breiger & Pattison (1986), p 239).
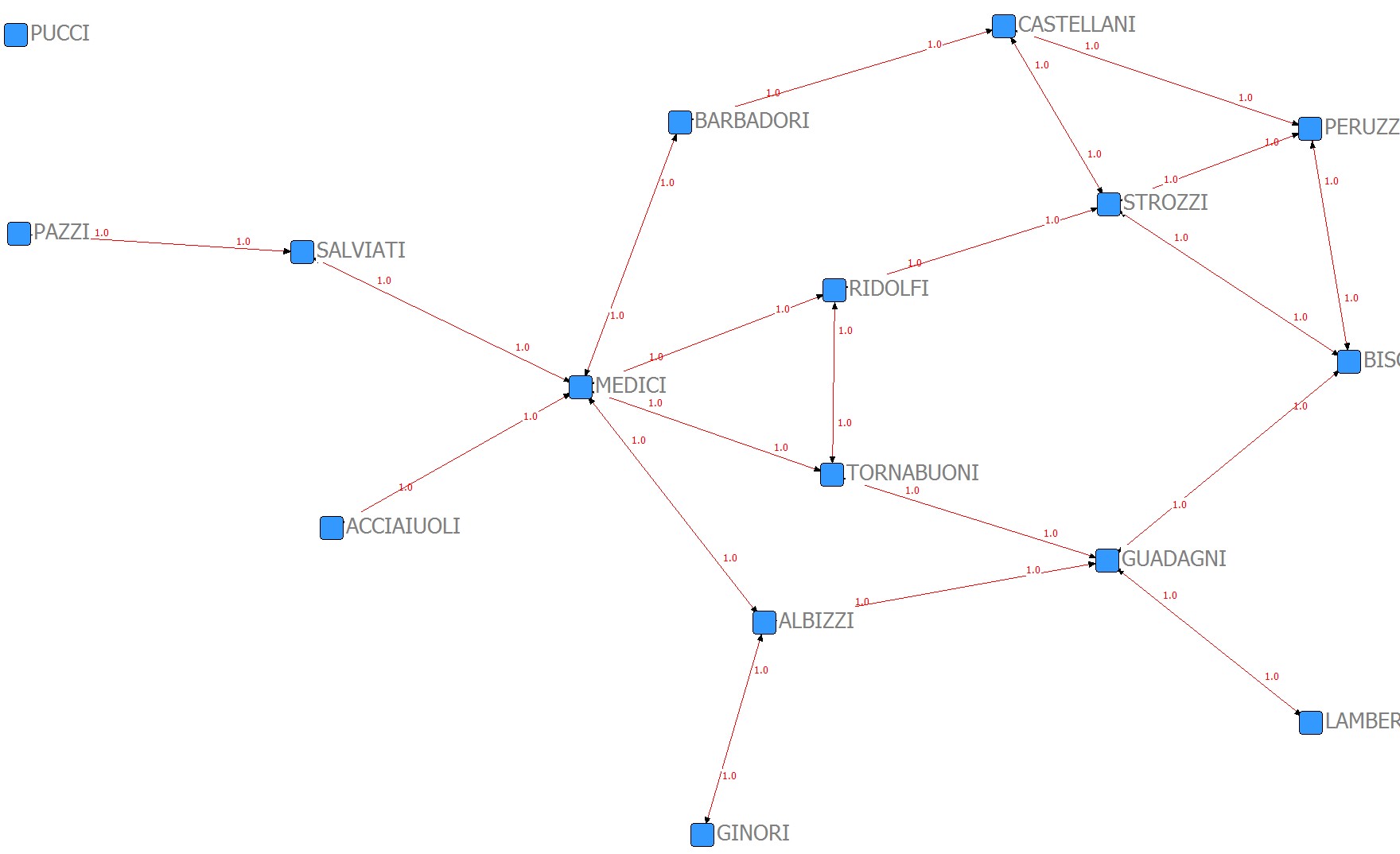
Substantively, the data include families who were locked in a struggle for political control of the city of Florence in around 1430. Two factions were dominant in this struggle: one revolved around the infamous Medicis (9), the other around the powerful Strozzis (15).
REFERENCES
- Breiger R. and Pattison P. (1986). Cumulated social roles: The duality of persons and their algebras. Social Networks, 8, 215-256. PDF
- Kent D. (1978). The rise of the Medici: Faction in Florence, 1426-1434. Oxford: Oxford University Press.
- Padgett, John F; Ansell, Christopher K. (1993). Robust action and the rise of the Medici, 1400-1434. The American Journal of Sociology, 98 (6). PDF
DL N=16 NM=2 FORMAT = FULLMATRIX DIAGONAL PRESENT ROW LABELS: ACCIAIUOL ALBIZZI BARBADORI BISCHERI CASTELLAN GINORI GUADAGNI LAMBERTES MEDICI PAZZI PERUZZI PUCCI RIDOLFI SALVIATI STROZZI TORNABUON COLUMN LABELS: ACCIAIUOL ALBIZZI BARBADORI BISCHERI CASTELLAN GINORI GUADAGNI LAMBERTES MEDICI PAZZI PERUZZI PUCCI RIDOLFI SALVIATI STROZZI TORNABUON LEVEL LABELS: PADGM PADGB DATA: 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
DL NR=16 NC=3 FORMAT = FULLMATRIX DIAGONAL PRESENT ROW LABELS: ACCIAIUOL ALBIZZI RIDOLFI STROZZI BARBADORI BISCHERI CASTELLAN GUADAGNI LAMBERTES MEDICI PAZZI PERUZZI SALVIATI TORNABUON GINORI PUCCI COLUMN LABELS: WEALTH #PRIORS #TIES DATA: 10 53 2 36 65 3 27 38 4 146 74 29 55 0 14 44 12 9 20 22 18 8 21 14 42 0 14 103 53 54 48 0 7 49 42 32 10 35 5 48 0 7 32 0 9 3 0 1
QAP result
QAP CORRELATION
--------------------------------------------------------------------------------
Data Matrices: PADGB
PADGM
# of Permutations: 5000
Random seed: 8954
Method: Fast: no missing values allowed
QAP results for PADGM * PADGB (5000 permutations)
1 2 3 4 5 6 7 8
Obs Value Significa Average Std Dev Minimum Maximum Prop >= O Prop <= O
--------- --------- --------- --------- --------- --------- --------- ---------
Pearson Correlation 0.3719 0.0016 0.0032 0.0944 -0.1690 0.4395 0.0016 0.9998
QAP Correlations
1 2
PADGB PADGM
----- -----
1 PADGB 1.000 0.372
2 PADGM 0.372 1.000
QAP P-Values
1 2
PADGB PADGM
----- -----
1 PADGB 0.000 0.002
2 PADGM 0.002 0.000
QAP statistics saved as datafile QAP Correlation Results
----------------------------------------
Running time: 00:00:01
Output generated: 12 5 16 08:44:36
UCINET 6.528 Copyright (c) 1992-2012 Analytic Technologies