Table of Contents
Categorical variables
2 groups
data:
elemapi2.sav
elemapi2_categories.sps
elemapi2.csv
in r
datavar <- read.csv("http://commres.net/wiki/_media/r/elemapi2.csv")
Variable Labels
Variable Position Label
snum 1 school number
dnum 2 district number
api00 3 api 2000
api99 4 api 1999
growth 5 growth 1999 to 2000
meals 6 pct free meals
ell 7 english language learners
yr_rnd 8 year round school 무방학학교 0 = 방학있음 1 = 방학없음
mobility 9 pct 1st year in school
acs_k3 10 avg class size k-3
acs_46 11 avg class size 4-6
not_hsg 12 parent not hsg
hsg 13 parent hsg
some_col 14 parent some college
col_grad 15 parent college grad
grad_sch 16 parent grad school
avg_ed 17 avg parent ed
full 18 pct full credential
emer 19 pct emer credential
enroll 20 number of students
mealcat 21 Percentage free meals in 3 categories
collcat 22 <none>
Variables in the working file
mealcat:
1 = 0-46% free meals
2 = 47-80
3 = 81-100
위의 변인들 중에서 “무방학학교”가 성적에 어떤 영향을 미칠 것인가를 알아 보기 위해서 regression 테스트를 시행하였다. 아래는 그 결과이다.
regression /dep api00 /method = enter yr_rnd.
| Model Summary | ||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | .475a | 0.226 | 0.224 | 125.3 |
| a. Predictors: (Constant), year round school | ||||
| ANOVA(b) | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 1825000.563 | 1 | 1825000.563 | 116.241 | .000a |
| Residual | 6248671.435 | 398 | 15700.179 | |||
| Total | 8073671.997 | 399 | ||||
| a. Predictors: (Constant), year round school b. Dependent Variable: api 2000 |
||||||
| Coefficients(a) | ||||||
| Unstandardized Coefficients | Standardized Coefficients | |||||
| Model | B | Std. Error | Beta | t | Sig. | |
| 1 | (Constant) | 684.539 | 7.14 | 95.878 | 0 | |
| year round school | -160.506 | 14.887 | -0.475 | -10.782 | 0 | |
| a. Dependent Variable: api 2000 | ||||||
위의 아웃풋을 살펴 보면,
학생들의 성적이 가지는 변량의 약 23%를 방학이없는학교가 갖으며, 이는 통계적으로 유의미한 것이다 (F(1, 398) = 116.241, p < .001). regression을 이용해서 엊어진 계수(coefficients)를 살펴 보면
$\hat{Y} = 684.539 - 160.506 X$
이 때,
- X: 0 = No
- X: 1 = Yes
이므로 x=0 일때를 대입해 보면, 즉, 방학이있는학교의 경우는 684.539의 추정치를 엊을 수 있으며, x=1일때를 대입해 보면 즉, 방학이없는학교의 경우에는 524.033의 추정치를 엊을 수 있다. b coefficient가 이 역할 (차이를 나타내는 역할을 하는데)에 대한 유의성에 대한 판단은 t-test로 하는데, 이 t값은 -10.782며 이는 F값인 116.241의 제곱근이다 (즉, $t^2 = F$ ). 사실, 이 상황은 정확히 t-test를 해야할 상황이므로 (두 그룹에 대한 성적평균의 차이), t-test를 해야 하지만 이와 같이 regression을 하여도 동일한 결과를 보게된다 (같은 의미에서 F-test를 했어도 마찬가지).
또한 위에서 이야기한 추정치는 X변인의 특성인 무방학학교과 일반학교의 평균과 같으며, X변인의 coefficient였던 -160.506은 바로, 이 두 평균 값의 차이를 없애 주는 역할을 한다.
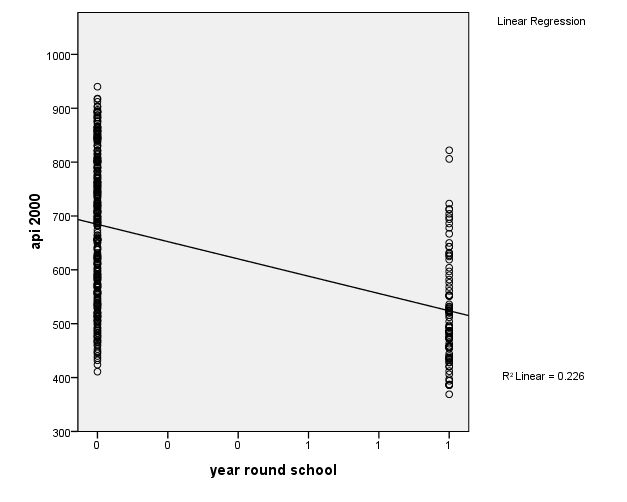
IGRAPH /X1 = VAR(yr_rnd) TYPE = scale /Y = VAR (api00) TYPE = SCALE /FITLINE METHOD = REGRESSION LINEAR LINE = TOTAL MEFFECT /CATORDER VAR(yr_rnd) (ASCENDING VALUES OMITEMPTY) /SCATTER COINCIDENT = NONE.
위의 그래프에서 직선은 $\hat{Y} = 684.539 - 160.506 X$ 이다.
MEANS TABLES=api00 BY yr_rnd.
| Report | |||
| api 2000 | |||
| year round school | Mean | N | Std. Deviation |
| No | 684.54 | 308 | 132.113 |
| Yes | 524.03 | 92 | 98.916 |
| Total | 647.62 | 400 | 142.249 |
이와 같이 종류변인(category, nominal)을 가지고서도 regression 테스트를 할 수 있으며, 사실 이는 t-test나 F-test와 다르지 않다. 위에서 주의해야 할 점은 두 변인의 종류를 coding할 때, 1과 2가 아닌, 0과 1로 하였다는 점이다. 이렇게 하는 이유는 해석하기에 편하기 때문이며, 이것이 보통의 방법이다. 그러나, 1과 2로 coding 데이터를 이용해도 크게 다른지 않은 결과를 구하게 된다. 다른 점이라면, 절편에 해당되는 상수값이 다르게 되며, coefficient값은 위의 분석과 동일한 값을 갖게 된다.
3 or more groups
만약에 ANOVA 테스트에서와 같이 종류가 3개 이상인 변인은 어떻게 처리해야 할까? 아래는 이를 regression으로 테스트 한 결과이다.
> mod2 <- lm(api00 ~ factor(mealcat), data=datavar)
> mod2
Call:
lm(formula = api00 ~ factor(mealcat), data = datavar)
Coefficients:
(Intercept) factor(mealcat)2 factor(mealcat)3
805.7 -166.3 -301.3
> summary(mod2)
Call:
lm(formula = api00 ~ factor(mealcat), data = datavar)
Residuals:
Min 1Q Median 3Q Max
-253.394 -47.883 0.282 52.282 185.620
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 805.718 6.169 130.60 <2e-16 ***
factor(mealcat)2 -166.324 8.708 -19.10 <2e-16 ***
factor(mealcat)3 -301.338 8.629 -34.92 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 70.61 on 397 degrees of freedom
Multiple R-squared: 0.7548, Adjusted R-squared: 0.7536
F-statistic: 611.1 on 2 and 397 DF, p-value: < 2.2e-16
>
아까와 같은 두 집단 간의 비교는 가능하였지만, 세 집단인 이 경우에 regression 테스트는 x를 연속변인으로 하는 선형관계를 구하게 된다. 즉, 두집단으로 이루어진 변인의 경우, 한 집단을 0으로 보았을 때 다른 집단은 자동으로 1이 되고, 이 둘을 비교하는 것이었는데, 3집단인 경우, 어느 한 집단을 0으로 놓고 본다고 비교할 집단이 두개나 되므로 비교가 어려워진다. 이는 현실에 맞지 않으므로 대개의 경우에는 집단 수에 해당하는 변인을 가외로 (가변인 혹은 dummy variable) 만든 후, 이를 가지고 regression을 하게 된다.
SPSS의 경우에는 아래와 같이 recode작업을 할 수 있다.
compute mealcat1 = 0. if mealcat = 1 mealcat1 = 1. compute mealcat2 = 0. if mealcat = 2 mealcat2 = 1. compute mealcat3 = 0. if mealcat = 3 mealcat3 = 1. execute.
위는 해당 카데고리를 1로 만들고, 나머지를 0으로 만들어서 2분화 하는 작업이다. 이렇게 하면 3개의 새로운 변인이 만들어지게 되는데 (mealcat1, mealcat2, mealcat3), 이 세개의 변인 중에서 2개만을 취해서 regression 테스트를 한다. SPSS의 경우에는
regression /dependent api00 /method = enter mealcat2 mealcat3. 주의. 세개의 변인을 모두 넣지 않는다.
Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .869a .755 .754 70.612 a. Predictors: (Constant), mealcat3, mealcat2 ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 6094197.670 2 3047098.835 611.121 .000a Residual 1979474.328 397 4986.081 Total 8073671.997 399 a. Predictors: (Constant), mealcat3, mealcat2 b. Dependent Variable: api 2000 Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) 805.718 6.169 130.599 .000 mealcat2 -166.324 8.708 -.550 -19.099 .000 mealcat3 -301.338 8.629 -1.007 -34.922 .000 a. Dependent Variable: api 2000
| Coefficients(a) | ||||||
| Unstandardized Coefficients | Standardized Coefficients | |||||
| Model | B | Std. Error | Beta | t | Sig. | |
| 1 | (Constant) | 805.718 | 6.169 | 130.599 | .000 | |
| mealcat2 | -166.324 | 8.708 | -.550 | -19.099 | .000 | |
| mealcat3 | -301.338 | 8.629 | -1.007 | -34.922 | .000 | |
| a. Dependent Variable: api 2000 | ||||||
위에서
$\hat{Y} = 805.718 - 166.324 \; \text{mealcat2} - 301.338 \; \text{mealcat3} $
이에 대한 해석은
- mealcat2와 mealcat3이 0일 때 (즉 mealcat1 변인의 상태일 때), 805.718
- mealcat3이 0일 때, 805.718-166.324 = 639.39 의 상황
- mealcat2가 0일 때, 805.718-301.338 = 504.38 의 상황이다.
- 그리고, 이 값들은 바로 각 그룹의 평균값이 된다.
Report api 2000 Percentage free meals in 3 categories Mean N Std. Deviation 0-46% free meals 805.72 131 65.669 47-80% free meals 639.39 132 82.135 81-100% free meals 504.38 137 62.727 Total 647.62 400 142.249
위에서, mealcat1대신에 mealcat3 그룹을 빼고 사용했어도, 결과를 해석하는데는 지장이 없다.
마지막으로, 위의 테스트는 이전에 언급되었던 FactorialAnova와 동일한 것이다.
glm api00 by mealcat /print=parameter.
| Between-Subjects Factors | |||
| Value Label | N | ||
| Percentage free meals in 3 categories | 1 | 0-46% free meals | 131 |
| 2 | 47-80% free meals | 132 | |
| 3 | 81-100% free meals | 137 | |
| Tests of Between-Subjects Effects | |||||
| Dependent Variable:api 2000 | |||||
| Source | Type III Sum of Squares | df | Mean Square | F | Sig. |
| Corrected Model | 6.094E6 | 2 | 3047098.835 | 611.121 | .000 |
| Intercept | 1.688E8 | 1 | 1.688E8 | 33863.695 | .000 |
| mealcat | 6094197.670 | 2 | 3047098.835 | 611.121 | .000 |
| Error | 1979474.328 | 397 | 4986.081 | ||
| Total | 1.758E8 | 400 | |||
| Corrected Total | 8073671.997 | 399 | |||
| a. R Squared = .755 (Adjusted R Squared = .754) | |||||
| Parameter Estimates | |||||||
| Dependent Variable:api 2000 | |||||||
| 95% Confidence Interval | |||||||
| Parameter | B | Std. Error | t | Sig. | Lower Bound | Upper Bound | |
| Intercept | 504.380 | 6.033 | 83.606 | .000 | 492.519 | 516.240 | |
| [mealcat=1] | 301.338 | 8.629 | 34.922 | .000 | 284.374 | 318.302 | |
| [mealcat=2] | 135.014 | 8.612 | 15.677 | .000 | 118.083 | 151.945 | |
| [mealcat=3] | 0a | . | . | . | . | . | |
| a. This parameter is set to zero because it is redundant. | |||||||
혹은 Oneway ANOVA
ONEWAY api00 BY mealcat /STATISTICS DESCRIPTIVES EFFECTS HOMOGENEITY /PLOT MEANS /MISSING ANALYSIS /POSTHOC=TUKEY SCHEFFE ALPHA(0.05).
| Sum of Squares | df | Mean Square | F | Sig. | |
| Between Groups | 6094197.67 | 2 | 3047098.835 | 611.120953 | .000 |
| Within Groups | 1979474.328 | 397 | 4986.08143 | ||
| Total | 8073671.998 | 399 |
2 variables, categorical
위에서 사용된 2 개의 독립변인을 모두 넣어서 regression을 할 수도 있다. 위에서 언급한 경로를 따른다면, 이는 FactorialAnova의 한 종류일 것이다.
regression /dep api00 /method = enter yr_rnd mealcat1 mealcat2.
| Model Summary | ||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | .876a | .767 | .765 | 68.893 |
| a. Predictors: (Constant), mealcat2, year round school, mealcat1 | ||||
| ANOVA(b) | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 6194144.303 | 3 | 2064714.768 | 435.017 | .000a |
| Residual | 1879527.694 | 396 | 4746.282 | |||
| Total | 8073671.997 | 399 | ||||
| a. Predictors: (Constant), mealcat2, year round school, mealcat1 | ||||||
| b. Dependent Variable: api 2000 | ||||||
| Coefficients(a) | ||||||
|---|---|---|---|---|---|---|
| Unstandardized Coefficients | Standardized Coefficients | |||||
| Model | B | Std. Error | Beta | t | Sig. | |
| 1 | (Constant) | 526.330 | 7.585 | 69.395 | .000 | |
| year round school | -42.960 | 9.362 | -.127 | -4.589 | .000 | |
| mealcat1 | 281.683 | 9.446 | .930 | 29.821 | .000 | |
| mealcat2 | 117.946 | 9.189 | .390 | 12.836 | .000 | |
| a. Dependent Variable: api 2000 | ||||||
똑같은 분석이지만 뒤의 두 변인의 효과를 따로 보기 위해서 뽑은 결과이다.
regression /dep api00 /method = enter yr_rnd /method = test(mealcat1 mealcat2).
| Model Summary | ||||
|---|---|---|---|---|
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | .475a | .226 | .224 | 125.300 |
| 2 | .876b | .767 | .765 | 68.893 |
| a. Predictors: (Constant), year round school b. Predictors: (Constant), year round school, mealcat2, mealcat1 |
||||
| ANOVA(d) | ||||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | R Square Change | ||
| 1 | Regression | 1825000.563 | 1 | 1825000.563 | 116.241 | .000a | ||
| Residual | 6248671.435 | 398 | 15700.179 | |||||
| Total | 8073671.997 | 399 | ||||||
| 2 | Subset Tests | mealcat1, mealcat2 | 4369143.740 | 2 | 2184571.870 | 460.270 | .000b | .541 |
| Regression | 6194144.303 | 3 | 2064714.768 | 435.017 | .000c | |||
| Residual | 1879527.694 | 396 | 4746.282 | |||||
| Total | 8073671.997 | 399 | ||||||
| a. Predictors: (Constant), year round school b. Tested against the full model. c. Predictors in the Full Model: (Constant), year round school, mealcat2, mealcat1. d. Dependent Variable: api 2000 |
||||||||
| Coefficients(a) | ||||||
|---|---|---|---|---|---|---|
| Unstandardized Coefficients | Standardized Coefficients | |||||
| Model | B | Std. Error | Beta | t | Sig. | |
| 1 | (Constant) | 684.539 | 7.140 | 95.878 | .000 | |
| year round school | -160.506 | 14.887 | -.475 | -10.782 | .000 | |
| 2 | (Constant) | 526.330 | 7.585 | 69.395 | .000 | |
| year round school | -42.960 | 9.362 | -.127 | -4.589 | .000 | |
| mealcat1 | 281.683 | 9.446 | .930 | 29.821 | .000 | |
| mealcat2 | 117.946 | 9.189 | .390 | 12.836 | .000 | |
| a. Dependent Variable: api 2000 | ||||||
| Excluded Variables(b) | ||||||
|---|---|---|---|---|---|---|
| Collinearity Statistics | ||||||
| Model | Beta In | t | Sig. | Partial Correlation | Tolerance | |
| 1 | mealcat1 | .697a | 23.132 | .000 | .758 | .914 |
| mealcat2 | -.138a | -3.106 | .002 | -.154 | .962 | |
| a. Predictors in the Model: (Constant), year round school b. Dependent Variable: api 2000 |
||||||
해석에 대해서 . . . .
| interpretation | |||
|---|---|---|---|
| mealcat=1 | mealcat=2 | mealcat=0 | |
| yr_rnd=0 | cell1 | cell2 | cell3 |
| yr_rnd=1 | cell4 | cell5 | cell6 |
| interpretation | |||
|---|---|---|---|
| mealcat=1 | mealcat=2 | mealcat=0 | |
| mealcat=1→1 | mealcat=2→1 | mealcat=3→mealcat1,2=0 | |
| yr_rnd=0 | cell1 | cell2 | cell3 |
| intercept + BMealCat1 | intercept + BMealCat2 | intercept | |
| yr_rnd=1 | cell4 | cell5 | cell6 |
| intercept + BMealCat1 + Byr_rnd | intercept + BMealCat2 + Byr_rnd | intercept + Byr_rnd |
|
glm api00 BY yr_rnd mealcat /DESIGN = yr_rnd mealcat /print=parameter TEST(LMATRIX).
continuous + categorical variables
regress /dep = api00 /method = enter yr_rnd some_col /save pre. * pre = predicted value (y hat). output: Model Summary(b) Model R R Square Adjusted R Square Std. Error of the Estimate 1 .507a .257 .253 122.951 a. Predictors: (Constant), parent some college, year round school b. Dependent Variable: api 2000 ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 2072201.839 2 1036100.919 68.539 .000a Residual 6001470.159 397 15117.053 Total 8073671.997 399 a. Predictors: (Constant), parent some college, year round school b. Dependent Variable: api 2000 Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) 637.858 13.503 47.237 .000 year round school -149.159 14.875 -.442 -10.027 .000 parent some college 2.236 553 .178 4.044 .000 a. Dependent Variable: api 2000
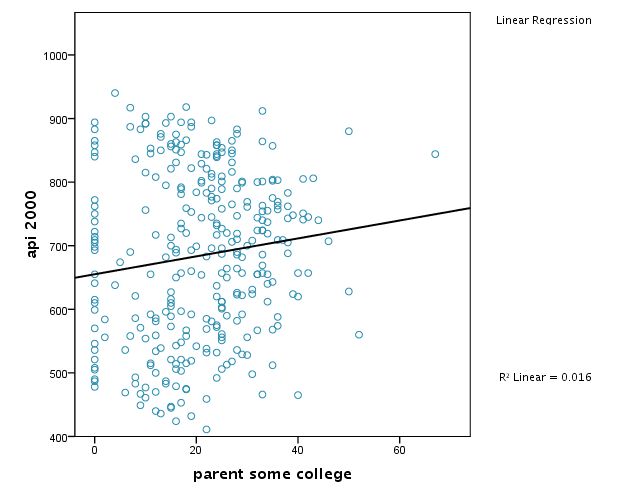
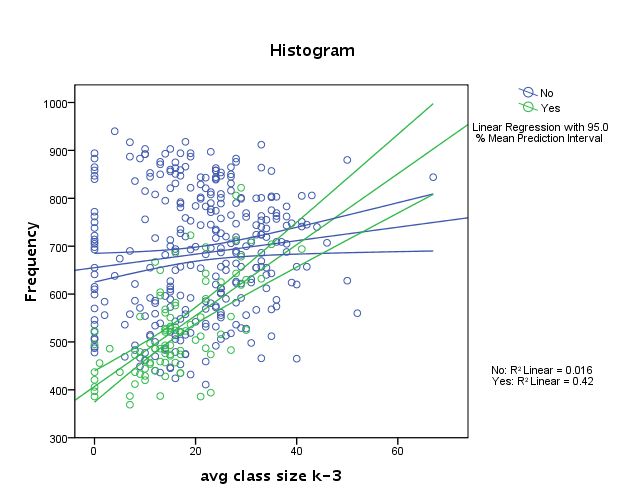
COMPUTE filt=(yr_rnd=0). FILTER BY filt. regress /dep = api00 /method = enter some_col.
위의 명령어는 (spss) yr_rnd value → 0 인것을 선택하여, 이를 필터링하면 (고르면) → 1 이 되고
필터링되지 않은 케이스들은 버려지게 되어 필터링이 된 케이스들만 선택이 되어 분석에 사용됨을 뜻 한다. 즉, 위는 rn_rnd값이 0 인 케이스에 대해서만 simple regression을 하라는 것이다.
Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .126a .016 .013 131.278 a. Predictors: (Constant), parent some college ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 84700.858 1 84700.858 4.915 .027a Residual 5273591.675 306 17233.960 Total 5358292.532 307 a. Predictors: (Constant), parent some college b. Dependent Variable: api 2000 Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) 655.110 15.237 42.995 .000 parent some college 1.409 .636 .126 2.217 .027 a. Dependent Variable: api 2000
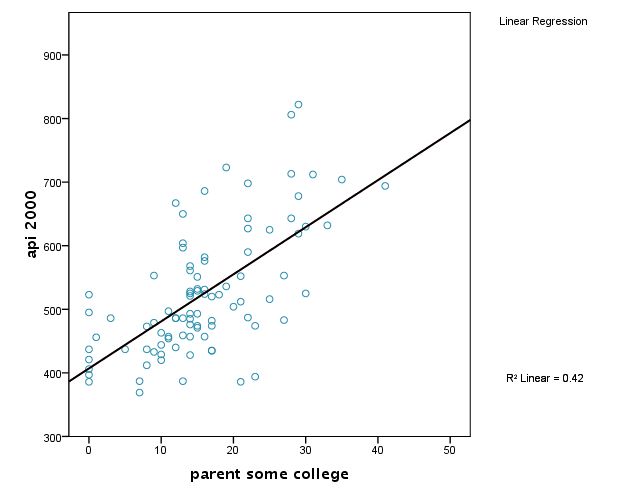
COMPUTE filt=(yr_rnd=1). FILTER BY filt. regress /dep = api00 /method = enter some_col. Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .648a .420 .413 75.773 a. Predictors: (Constant), parent some college ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 373644.064 1 373644.064 65.078 .000a Residual 516734.838 90 5741.498 Total 890378.902 91 a. Predictors: (Constant), parent some college b. Dependent Variable: api 2000 Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) 407.039 16.515 24.647 .000 parent some college 7.403 .918 .648 8.067 .000 a. Dependent Variable: api 2000
interaction effect
위의 두 regression은 yr_rnd 변인이 갖는 두 가지 특성에 대해서 따로 regression (api_00 ← some_col) 을 한 것이다. 이 결과, 두 집단의 regression 기울기 (coefficient)가 다르다는 것을 알았다. 즉, some_col의 api_00에 대한 영향력이 다르다는 것이다. 이는 각각의 상황(변인의 특성)에 따라서 동일한 독립변인이 역할을 달리하는 것으로 상호효과(interaction effect)라고 할 수 있다. 따라서, 두 기울기가 혹은 계수(coefficients)가 서로 다르다는 것을 검증한다면, 상호효과를 알아볼 수 있다.
아래는 새로운 변인을 만들어서 변인의 값으로 yr_rnd와 some_col값을 곱한 값을 대체한 것이다. 즉,
DV: api00
IV1: some_col
IV2: yr_rnd
IV3: yr_rnd * some_col = interaction effects
compute yrXsome = yr_rnd*some_col. execute.
그리고, 이 변인을 regression 공식에 이용한다.
regress /dep = api00 /method = enter some_col yr_rnd yrXsome /save pre.
output: Model Summary(b) Model R R Square Adjusted R Square Std. Error of the Estimate 1 .532a .283 .277 120.922 a. Predictors: (Constant), yrXsome, parent some college, year round school b. Dependent Variable: api 2000 ANOVA(b) Model Sum of Squares df Mean Square F Sig. 1 Regression 2283345.485 3 761115.162 52.053 .000a Residual 5790326.513 396 14622.037 Total 8073671.997 399 a. Predictors: (Constant), yrXsome, parent some college, year round school b. Dependent Variable: api 2000 Coefficients(a) Unstandardized Coefficients Standardized Coefficients Model B Std. Error Beta t Sig. 1 (Constant) 655.110 14.035 46.677 .000 parent some college 1.409 .586 .112 2.407 .017 year round school -248.071 29.859 -.735 -8.308 .000 __yrXsome__ 5.993 1.577 .330 3.800 .000 a. Dependent Variable: api 2000 Residuals Statistics(a) Minimum Maximum Mean Std. Deviation N Predicted Value 407.04 749.54 647.62 75.648 400 Residual -275.118 279.252 .000 120.466 400 Std. Predicted Value -3.180 1.347 .000 1.000 400 Std. Residual -2.275 2.309 .000 .996 400 a. Dependent Variable: api 2000
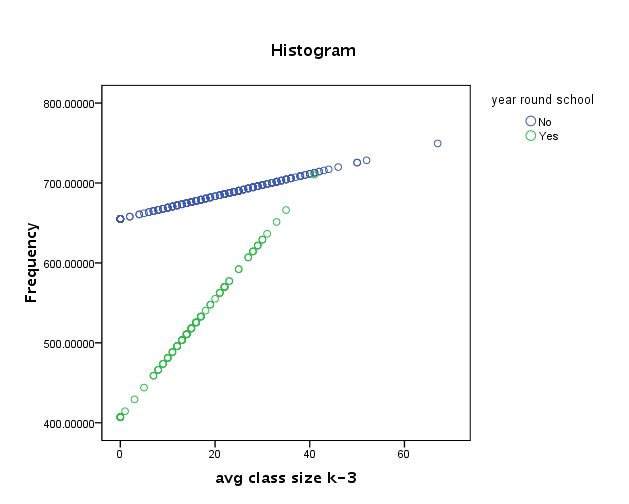
위에서 yr_rnd의 b 계수 값이 5.993으로 유의미하다고 판단된다 (t = 3.800, p < .001). 따라서 두 변인 간의 상호효과가 존재한다고 할 수 있다. 이를 다시 도표화해서 보면, 두 집단의 기울기가 서로 다르다는 것을 알 수 있다.
위의 테스트를 살펴보면, 두 개의 독립변인 중 하나는 종류변인이고 다른 하나는 숫자변인이다. 각 변인의 영향력에 대해서 regression을 통해서 알아보면서 두 변인의 상호작용까지 알아본 것이 된다. 이와 같은 절차는 FactorialAnova 에서 살펴본 것과 같다. 사실, 위의 연구문제(가설)를 ANOVA를 이용해서도 할 수 있다.
glm api00 BY yr_rnd WITH some_col /DESIGN = some_col yr_rnd yr_rnd*some_col. or UNIANOVA api00 BY yr_rnd WITH some_col /DESIGN=yr_rnd some_col some_col*yr_rnd /print=parameter .