Table of Contents
Logistic Regression
https://www.bookdown.org/rwnahhas/RMPH/blr-orlr.html
data: https://www.bookdown.org/rwnahhas/RMPH/appendix-nsduh.html#appendix-nsduh
Data preparation
- Extract the .RData file NSDUH_2019.RData from the .zip file.
- Download the R script files NSDUH_2019 Process.R and NSDUH_2019 MI Simulation.R from RMPH Resources.
- Run the R script file NSDUH_2019 Process.R to process the raw data and create the following teaching datasets:
- nsduh2019_rmph.RData
- nsduh2019_adult_sub_rmph.RData
- Place these .Rdata files in your “Data” folder.
- Run the R script file NSDUH_2019 MI Simulation.R to process the raw data and create the following teaching datasets:
- nsduh_mar_rmph.RData
- Place this .Rdata file in your “Data” folder.
getwd()
# 보통 C:/Users/Username/Documents/
setwd("~/rData")
Odds
Odds (승산): 한 사건이 일어날 확률과 그 반대의 확률 (일어나지 않을 확률) 간의 비율 한 사건이 일어날 확률과 다름에 주의하라.
\begin{align}
\displaystyle \frac {p} {1-p}
\end{align}
- 한 사건이 일어날 확률이 75%라고 하면
- 그 사건이 일어나지 않을 확률은 25%이므로
- 그 사건의 승산은 (odds) $ 75\%/25\% = 3:1 $
- 3대1 (혹은 3) 이라고 읽는다
- 이에 반해서 그 사건이 일어날 확률은 (애초에) 75% 라고 했음
- 내가 파티에 가서 입구에서 당첨번호를 받았다
- 당첨번호를 받은 사람은 나를 제외하고 4명이 더 있다
- 내가 상품에 당첨이 될 확률은 $1/5=20\%$ 이다
- 그러나 내가 상품에 당첨이 될 odds는 (승산은?)
- 1 대 4 이다 $(1:4, (25\%))$
- 한 사건의 probability 가 0.5보다 크다면, 그 사건이 일어날 승산은 (odds) 1보다 크다
- 한 사건의 prob가 0.5보다 크다면 == 한사건의 일어날 odds가 내게 유리하다면
- $odds = \frac {p}{1-p} = \frac {0.6}{1-0.6} = 1.5 $
- 반대로 0.5보다 작으면 승산은 1보다 작게 된다.
- $odds = \frac {p}{1-p} = \frac {0.4}{1-0.4} = 0.667 $
- 위의 설명은
- odds의 분포는 1을 중심으로 0-1에는 내게 불리한 odds가 나타나고
- 1-무한대 에서는 유리한 odds가 나타나게 된다.
- see ln_성질
- 양쪽이 언발란스한데, 이것을 없애는 방법에 log를 붙이는 것이 있다
- odds, 1/6 와 odds 6/1에 log를 붙이면
> log(1/6) [1] -1.791759 > log(6) [1] 1.791759 >
Odds ratio
Odds ratio (승비): Odds ratio는 두 odds 간의 비율을 말한다.
- 질병 X에 걸리 확률이 남자는 $35\%$ 이고 여자는 $25\%$라고 하면
- 남자가 질병에 걸릴 승산은 $\frac {.35} {(1 - .35)} = .54$ 이고
- 여자가 질병에 걸릴 승산은 $\frac {.25} {(1 - .25)} - .33$ 이다.
- 그리고 odds ratio는 $ \frac {.54} {.33} = 1.64$ 이다.
- wald test
##########
# see youtube
# https://youtu.be/8nm0G-1uJzA
n.mut <- 23+117
n.norm <- 6+210
p.cancer.mut <- 23/(23+117)
p.cancer.norm <- 6/(6+210)
set.seed(1011)
c <- runif(n.mut, 0, 1)
# 0 = not cancer, 1 = cancer among mutant gene
mutant <- ifelse(c>=p.cancer.mut, 0, 1)
c <- runif(n.norm, 0, 1)
# 0 = not cancer, 1 = cancer among normal gene
normal <- ifelse(c>=p.cancer.norm, 0, 1)
# 0 = mutant; 1 = normal
gene <- c(rep(0, length(mutant)), rep(1, length(normal)))
# 0 = not cancer; 1 = cancer
cancer <- c(mutant, normal)
df <- as.data.frame(cbind(gene, cancer))
df
df$gene <- factor(df$gene, levels = c(0,1), labels = c("mutant", "norm"))
df$cancer <- factor(df$cancer, levels = c(0,1), labels = c("nocancer", "cancer"))
df
tab <- table(df)
tab
tab[1,2]
tab[1,1]
# p.c.m = p.cancer.mut the above
p.cancer.mutant <- tab[1,2]/(tab[1,1]+tab[1,2])
p.nocancer.mutant <- tab[1,1]/(tab[1,1]+tab[1,2])
p.cancer.mutant
1-p.cancer.mutant
p.nocancer.mutant
p.cancer.norm <- tab[2,2]/(tab[2,1]+tab[2,2])
p.nocancer.norm <- 1-p.cancer.norm
p.cancer.norm
p.nocancer.norm
odds(p.cancer.mutant)
odds(p.cancer.norm)
odds.ratio(p.cancer.mutant, p.cancer.norm)
> ##########
> # see youtube
> # https://youtu.be/8nm0G-1uJzA
> n.mut <- 23+117
> n.norm <- 6+210
> p.cancer.mut <- 23/(23+117)
> p.cancer.norm <- 6/(6+210)
>
> set.seed(1011)
> c <- runif(n.mut, 0, 1)
> # 0 = not cancer, 1 = cancer among mutant gene
> mutant <- ifelse(c>=p.cancer.mut, 0, 1)
>
> c <- runif(n.norm, 0, 1)
> # 0 = not cancer, 1 = cancer among normal gene
> normal <- ifelse(c>=p.cancer.norm, 0, 1)
>
> # 0 = mutant; 1 = normal
> gene <- c(rep(0, length(mutant)), rep(1, length(normal)))
> # 0 = not cancer; 1 = cancer
> cancer <- c(mutant, normal)
>
> df <- as.data.frame(cbind(gene, cancer))
> df
gene cancer
1 0 0
2 0 1
3 0 0
4 0 0
5 0 0
6 0 0
>
> df$gene <- factor(df$gene, levels = c(0,1), labels = c("mutant", "norm"))
> df$cancer <- factor(df$cancer, levels = c(0,1), labels = c("nocancer", "cancer"))
> df
gene cancer
1 mutant nocancer
2 mutant cancer
3 mutant nocancer
4 mutant nocancer
5 mutant nocancer
6 mutant nocancer
>
> tab <- table(df)
> tab
cancer
gene nocancer cancer
mutant 121 19
norm 210 6
> tab[1,2]
[1] 19
> tab[1,1]
[1] 121
>
> # p.c.m = p.cancer.mut the above
> p.cancer.mutant <- tab[1,2]/(tab[1,1]+tab[1,2])
> p.nocancer.mutant <- tab[1,1]/(tab[1,1]+tab[1,2])
> p.cancer.mutant
[1] 0.1357143
> 1-p.cancer.mutant
[1] 0.8642857
> p.nocancer.mutant
[1] 0.8642857
>
> p.cancer.norm <- tab[2,2]/(tab[2,1]+tab[2,2])
> p.nocancer.norm <- 1-p.cancer.norm
> p.cancer.norm
[1] 0.02777778
> p.nocancer.norm
[1] 0.9722222
>
> odds(p.cancer.mutant)
[1] 0.1570248
> odds(p.cancer.norm)
[1] 0.02857143
> odds.ratio(p.cancer.mutant, p.cancer.norm)
[1] 5.495868
>
Logit 성질
여기서
\begin{align*}
ln(x) & = y \\
log_e {x} & = y \\
x & = e^{y} \\
\end{align*}
위에서
- $ \text{if } \;\;\; x = 1, $
- $ e^{y} = 1 $ 이므로
- $ y = 0 $
- $ \therefore \;\; log_{e}(1) = 0 $
- $\text{if } \;\;\; x = 0 $
- $ 0 = e^{y} $ 이므로
- y 는 $ - \infty $
- 왜냐하면, $ e^{-\infty} = \frac {1}{e^{\infty}} = \frac {1}{\infty} = 0 $ 혹은 $0$ 에 수렴하기 때문
- $ \therefore \;\; log_{e}(0) = - \infty $
- $\text{if } \;\;\; x = \infty $
- $ \infty = e^{y} $ 이므로
- $ y = \infty $ 어야 함
- $ \therefore \;\; log_{e}(\infty) = + \infty $
- Odds 는 확률 $0.5$를 기준으로 $0-1$ 과 $1-\infty$ 범위를 갖는다고 하였는데
- 이 Odds에 log를 씌우면 그 범위는
- $-\infty$ 에서 $\infty $가 되어서 a+bX에 맞춰서 해석을 할 수 있게 된다.
> load("nsduh2019_adult_sub_rmph.RData")
> # Shorter name
> nsduh <- nsduh_adult_sub
> tab <- table(nsduh$demog_sex, nsduh$mj_lifetime)
> tab
No Yes
Male 206 260
Female 285 249
>
# Marijuana experience (me) in lifetime NO YES Male 206 260 466 Female 285 249 534 491 509 1000 P(me among males) = 260 / 466 = 0.5579399 P(me among females) = 249 / 534 = 0.4662921 Odds for males = 260 / 206 = 1.262136 Odds for females = 249 / 285 = 0.8736842 Odds ratio between males and females = (260 / 206) / (249 / 285) = 1.262136 / 0.8736842 = 1.444613
odds <- function(p) p/(1-p) odds.ratio <- function(p1, p2) odds(p1)/odds(p2) logit <- function(p) log(p/(1-p)) ilogit <- function(x) exp(x)/(1+exp(x)) # exp() is the exponential function
pm <- tab[1,2]/(tab[1,1]+tab[1,2]) pf <- tab[2,2]/(tab[2,1]+tab[2,2]) om <- odds(pm) of <- odds(pf) ormf <- odds.ratio(pm,pf) pm pf om of ormf > pm [1] 0.5579399 > pf [1] 0.4662921 > om [1] 1.262136 > of [1] 0.8736842 > ormf [1] 1.444613 > x1 <- logit(pm) x2 <- logit(pf) x1 x2 ilogit(x1) ilogit(x2) > x1 <- logit(pm) > x2 <- logit(pf) > x1 [1] 0.2328055 > x2 [1] -0.1350363 > ilogit(x1) [1] 0.5579399 > ilogit(x2) [1] 0.4662921 > >
Logitistic Regression Analysis
\begin{align*} \displaystyle ln \left( {\frac{p}{(1-p)}} \right) = a + bX \end{align*}
- p = 변인 X가 A일 확률
- 1-p = 변인 X가 A가 아닐 확률
- ln 은 e를 밑으로 하는 log 를 말한다
- $ln \left( {\frac{p}{(1-p)}} \right) $ 을 $\text{logit(p)}$ 로 부른다
\begin{align} ln \left( {\frac{p}{1-p}} \right) & = a + bX \nonumber \\ \frac{p}{1-p} & = e^{a+bX} \nonumber \\ p & = e^{a+bX} * (1-p) \nonumber \\ p & = e^{a+bX} - p * \left(e^{a+bX} \right) \nonumber \\ p + p * \left(e^{a+bX} \right) & = e^{a+bX} \nonumber \\ p * \left(1 + e^{a+bX} \right) & = e^{a+bX} \nonumber \\ p & = \frac {e^{a+bX}} { \left(1 + e^{a+bX} \right)} \\ \end{align}
- 위에서 계수 b값이 충분히 커서 X 가 커지면 p 값은 1로 수렴하고
- b값이 충분히 작아서 X가 아주 작아지면 p 값은 0에 가까이 간다
- 즉 ln(p/(1-p))는 직선의 관계를 갖지만 (a+bX)
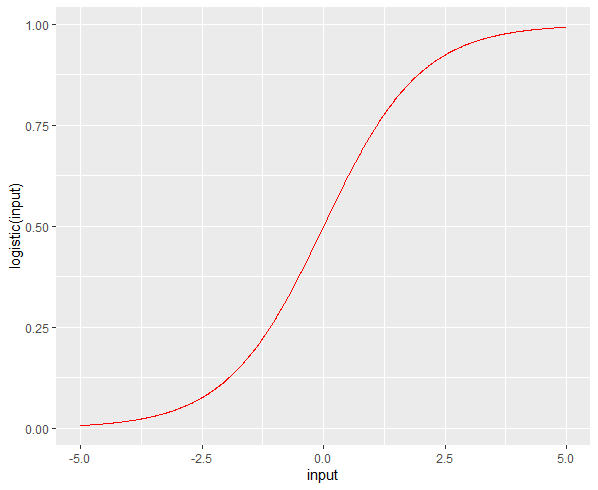
- p값은 0에서 1사이의 값을 갖게 된다.
- p의 그래프는 아래와 같은 곡선이다.
install.packages("sigmoid")
library(sigmoid)
library(ggplot2)
input <- seq(-5, 5, 0.01)
df = data.frame(input, logistic(input), Gompertz(input))
ggplot( df, aes(input, logistic(input)) ) +
geom_line(color="red")
Binary Logistic Regression
독립변인이 종류일 때에
IVs: categorical or numerical variables
DV: categorical variable
\begin{align} ln \left( {\frac{p}{(1-p)}} \right) & = a + bX \\ \end{align}
- $p$ = probability of an event happening
- $(1-p)$ = probability of an event NOT happening
- $p/(1-p)$ : odds of the event
- $ln (p/(1-p))$ : natural logarithm of the odds : log-odds or logit
- to get the odds from the above logit, we use the inverse of natural logarithm
- from $ln (p/(1-p)) = x$ OR $Log(odds) = x$
- to $p/(1-p) = odds = e^x$
- to convert log odds to probability $p$,
- we use inverse login function $e^x/(1 + e^x) = 0.4662912$
intercept (절편) 해석
- 위의 식 [2]에서 $X=0$ 일 경우 (현재 binary IV에 대해서 이야기하고 있음에 주의),
- $ln(p/(1-p) = a$ 에서
- (모든) 독립변인이 0의 값을 가질 때 (독립변인이 0이 되는 경우 = 기준 category일 경우),
- 절편 값 $a$ 는 로짓값을 (log-odds 값 $ln(p/(1-p)$) 갖게 된다.
- 따라서 $ p = \displaystyle \frac {e^a}{1+e^a}$
- 아래 아웃풋에서 $a = -0.13504$ 이므로
- $ p = \displaystyle \frac {e^{-0.13504}}{1+e^{-0.13504}} = 0.4662912$
- 위는 정의된 평션으로 (ilogit) 구해도 된다
ilogit(a) = 0.4662912 - 마지막으로 이 값은 우리가 이미 table에서 구한 probability of female yes 값과 (
PF.yes) 같다.
odds <- function(p) p/(1-p) odds.ratio <- function(p1, p2) odds(p1)/odds(p2) # log odds를 구하는 function logit <- function(p) log(p/(1-p)) # probability를 구하는 function # p = e^x/(1+e^x) ilogit <- function(x) exp(x)/(1+exp(x))
# 절편 해석 e^-0.13504/(1 + e^-0.13504) # 위의 절편에 대한 p 값 계산 # p = e^x/1+e^x summary(fit.ex6.2)$coefficient # coefficient 값들 출력 summary(fit.ex6.2)$coefficient[1,1] # 절편 값 출력 # or coef(fit.ex6.2)["(Intercept)"] # coef(fit.ex6.2)[1] p <- ilogit(summary(fit.ex6.2)$coefficient[1,1]) p # 이 값은 PF.yes 값과 같다 PF.yes
Odds ratio in logistic
\begin{align*} ln(\frac{p}{1-p}) = & y \\ \frac {p}{1-p} = & e^{y} \;\;\; \text{where } \;\; y = a + bX \\ \text {odds} = & e^{y} = e^{a + bX} \\ \text{then} \;\;\; \text{odds ratio} (y_{2}/y_{1}) = & \text {odds ratio between } \\ & \text{odds of y at one point, } y_1 \text { and } \\ & \text{odds of y at another point, } y_2 \\ \text{and } y_1 = & a + b (X) \\ y_2 = & a + b (X+1) \\ \text{then } & \;\; \\ \text {odds of } y_1 = & e^{(a+b(X))} \\ \text {odds of } y_2 = & e^{(a+b(X+1))} \\ \text {odds ratio for } y_1 = & \frac {e^{(a+bX+b)} } {e^{(a+bX)}} \\ = & \frac {e^{(a+bX)} * e^{b}} {e^{(a+bX)} } \\ = & e^b \end{align*}
- 위의 $e^b$ 가 의미하는 것은 $X$가 한 유닛만큼 증가하면 $Y$는 $b$만큼 증가하는 것이 되는데 이 $b$는
- $y2$와 $y1$ 간의 $\text{log of odds ratio}$ 로 이해되어야 한다. 따라서
- y2와 y1 간의 $\text{odds ratio} = e^b $ 이 된다.
coefficient (계수) 해석
- $X = 1$ 일 경우 $ln(odds) = a + bX = a + b $
- 아래 아웃 풋에서
- a = (Intercept) = -0.13504
- b = demog_sexMale = 0.36784
- 따라서 $a + b = -0.13504 + 0.36784 = 0.2328 $
- 즉, $ln(odds) = 0.2328 $ 이고
- $ odds = \displaystyle \frac {p_{\text{ of male yes}}}{p-1} = e^{0.2328} = 1.262129$ 이것은 X가 1일 경우이다.
- $ p = e^{0.2328} / (1 + e^{0.2328}) = 0.5579386 $ 그리고 X는 1일 경우의 prob = 0.558 정도이다.
- or
ilogit(0.2328) = 0.5579386
- coefficient값 (0.36784) 은 아래처럼 구할 수도 있다
summary(fit.ex6.2)$coefficient[2,1]- $e^{b}$ 값은 male vs female 의 yes에 대한 odds ratio 를 말한다
- why?
om/of = 1.444613orodds.ratio(pm, pf) = 1.444613- 즉, $log(om/of) = b$
- $log(1.444613) = b$
- $ 1.444613 = e^b$
> log(1.444613) [1] 0.3678415 # 이는 계수 값 b값이다. > b <- summary(fit.ex6.2)$coefficient[2,1] > b [1] 0.3678417 > e^b [1] 1.444613 >
- 이 값은 앞서 tab에서 구한 odds ratio 이다 (male odds / female odds = om/of).
- X = 0 (female)에서 X = 1 (male) 로 바뀔때의 odds ratio는 1.444613으로
- 남자의 마리화나 경험이 여성에 비해 44.5% 증가한다고 해석
glm in R
nsduh <- nsduh %>%
mutate(demog_sex = relevel(demog_sex, ref = "Female"))
fit.ex6.2 <- glm(mj_lifetime ~ demog_sex,
family = binomial, data = nsduh)
summary(fit.ex6.2)
# install.packages("dplyr")
# library(dplyr)
> nsduh <- nsduh %>%
+ mutate(demog_sex = relevel(demog_sex, ref = "Female"))
> fit.ex6.2 <- glm(mj_lifetime ~ demog_sex,
+ family = binomial, data = nsduh)
> summary(fit.ex6.2)
Call:
glm(formula = mj_lifetime ~ demog_sex, family = binomial, data = nsduh)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.13504 0.08675 -1.557 0.11954
demog_sexMale 0.36784 0.12738 2.888 0.00388 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1386.0 on 999 degrees of freedom
Residual deviance: 1377.6 on 998 degrees of freedom
AIC: 1381.6
Number of Fisher Scoring iterations: 3
>
CI of b coefficient
fit.ex6.2에서
# 위의 b값에 대한 CI을 구하기 위해서 confint 펑션을 사용한다 confint(fit.ex6.2) # b값에 대한 것만 알고 싶으므로 (drop = F는 confint(fit.ex6.2)[2, , drop=F] # 그리고 이 값들의 실제 odds ratio값을 보려면 exp(confint(fit.ex6.2)[2, , drop=F])
> # 위의 b값에 대한 CI을 구하기 위해서 confint 펑션을 사용한다
> confint(fit.ex6.2)
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) -0.3054835 0.03475989
demog_sexMale 0.1185985 0.61808060
> # b값에 대한 것만 알고 싶으므로
> confint(fit.ex6.2)[2, , drop=F]
Waiting for profiling to be done...
2.5 % 97.5 %
demog_sexMale 0.1185985 0.6180806
> # 그리고 이 값들의 실제 odds ratio값을 보려면
> exp(confint(fit.ex6.2)[2, , drop=F])
Waiting for profiling to be done...
2.5 % 97.5 %
demog_sexMale 1.125918 1.855363
>
coefficient값에 대한 테스트
일반 regression에서 b값은 t-test를 했지만 여기서는 z-test를 (Wald test) 한다. 이는 IV가 종류이거나 숫자일 때 모두 마찬가지이다.
# install.packages("car")
# library(car)
# coefficient probability test
car::Anova(fit.ex6.2, type = 3, test.statistic = "Wald")
> # coefficient probability test
> car::Anova(fit.ex6.2, type = 3, test.statistic = "Wald")
Analysis of Deviance Table (Type III tests)
Response: mj_lifetime
Df Chisq Pr(>Chisq)
(Intercept) 1 2.4233 0.11954
demog_sex 1 8.3394 0.00388 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
마리화나의 사용경험에서 남성이 여성보다 큰 승산이 있다고 판단되었다 (Odds ratio (OR) = 1.44; 95% CI = 1.13, 1.86; p = .004). 남성은 여성보다 약 44% 더 사용경험을 할 승산을 보였다 (OR = 1.44).
exercise: binary IV
######################################## # exercise head(df) table(df) # base 바꾸기 df.norm <- df %>% mutate(gene = relevel(gene, ref = "norm")) df.mut <- df %>% mutate(gene = relevel(gene, ref = "mutant")) logm.cancer.gene.1 <- glm(cancer ~ gene, family = binomial, data = df.norm) summary(logm.cancer.gene.1) a <- logm.cancer.gene.1$coefficients[1] b <- logm.cancer.gene.1$coefficients[2] a b a+b # when b = 0; 즉, mutant = 0 일 때 # log(odds.norm) = a 이므로 # odds.norm = e^a exp(a) # 확인 odds(p.can.norm) # odds.mut = e^(a+b) exp(a+b) odds(p.can.mut) # odds.ratio = e^(b) exp(b) odds.ratio(p.can.mut, p.can.norm) logm.cancer.gene.2 <- glm(cancer ~ gene, family = binomial, data = df.mut) summary(logm.cancer.gene.2) a <- logm.cancer.gene.2$coefficients[1] b <- logm.cancer.gene.2$coefficients[2] a b a+b # when b = 0; 즉, mutant = 0 일 때 # log(odds.norm) = a 이므로 # odds.norm = e^a exp(a) # 확인 odds(p.can.mut) # odds.mut = e^(a+b) exp(a+b) odds(p.can.norm) # odds.ratio = e^(b) exp(b) odds.ratio(p.can.norm, p.can.mut)
X: numeric variable
########################################
########################################
########################################
# numeric IV
fit.ex6.3 <- glm(mj_lifetime ~ alc_agefirst, family = binomial, data = nsduh)
round(summary(fit.ex6.3)$coef, 4)
ilogit(coef(fit.ex6.3)["(Intercept)"])
# 0.9952 = prob of starting marijuana when age is 0
# when the age is zero (intercept이므로)
# age = 0 에서 추정하는 것은 이상함
summary(nsduh$alc_agefirst)
# 위의 아웃풋에서 Mean값이 약 17이므로 17을
# 기준으로 하여 다시 보면
# install.packages("dplyr") # for %>% function
# library(dplyr)
# install.packages("tidyverse") # for mutate function
# library(tidyverse)
nsduh <- nsduh %>%
mutate(calc_agefirst = alc_agefirst - 17)
fit.ex6.3.centered <- glm(mj_lifetime ~ calc_agefirst,
family = binomial, data = nsduh)
fit.ex6.3.centered
ilogit(coef(fit.ex6.3.centered)["(Intercept)"])
# b coefficient
# 17살일 때를 기준으로 한살씩 증가할 때마다의
# 마리화나 경험/비경험의 Odds ratio는 -0.2835
# 이를 수치화하면
exp(coef(fit.ex6.3.centered)["calc_agefirst"])
# 이는 17이후에 한살씩 알콜처음 경험을 늦추면
# 마리화나 경험율 대 미경험 odds ratio가
# 0.247 낮아진다고 할 수 있다 (0.7531 증가는)
# 1-0.7531로 보는 것
# 그리고 이에 대한 CI를 보면 아래와 같고
confint(fit.ex6.3.centered)[2, , drop = F]
# 이를 승비로 (odds ratio) 보면
exp(confint(fit.ex6.3.centered)[2, , drop = F])
> ########################################
> ########################################
> ########################################
> # numeric IV
> fit.ex6.3 <- glm(mj_lifetime ~ alc_agefirst, family = binomial, data = nsduh)
> round(summary(fit.ex6.3)$coef, 4)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.3407 0.4747 11.2510 0
alc_agefirst -0.2835 0.0267 -10.6181 0
>
> ilogit(coef(fit.ex6.3)["(Intercept)"])
(Intercept)
0.9952302
> # 0.9952 = prob of female starting marijuana
> # when the age is zero (intercept이므로)
>
> # age = 0 에서 추정하는 것은 이상함
> summary(nsduh$alc_agefirst)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
3.00 15.00 17.00 17.49 19.00 45.00 157
>
> # 위의 아웃풋에서 Mean값이 약 17이므로 17을
> # 기준으로 하여 다시 보면
>
> nsduh <- nsduh %>%
+ mutate(calc_agefirst = alc_agefirst - 17)
> fit.ex6.3.centered <- glm(mj_lifetime ~ calc_agefirst,
+ family = binomial, data = nsduh)
> fit.ex6.3.centered
Call: glm(formula = mj_lifetime ~ calc_agefirst, family = binomial,
data = nsduh)
Coefficients:
(Intercept) calc_agefirst
0.5207 -0.2835
Degrees of Freedom: 842 Total (i.e. Null); 841 Residual
(157 observations deleted due to missingness)
Null Deviance: 1141
Residual Deviance: 968.4 AIC: 972.4
> ilogit(coef(fit.ex6.3.centered)["(Intercept)"])
(Intercept)
0.6273001
>
> # b coefficient
> # 17살일 때를 기준으로 한살씩 증가할 때마다의
> # 마리화나 경험/비경험의 Odds ratio는 -0.2835
> # 이를 수치화하면
> exp(coef(fit.ex6.3.centered)["calc_agefirst"])
calc_agefirst
0.7531198
>
> # 이는 17이후에 한살씩 알콜처음 경험을 늦추면
> # 마리화나 경험율 대 미경험 odds ratio가
> # 0.247로 낮아진다고 할 수 있다 (0.7531 증가는)
> # 1-0.7531로 보는 것
>
> # 그리고 이에 대한 CI를 보면 아래와 같고
> confint(fit.ex6.3.centered)[2, , drop = F]
Waiting for profiling to be done...
2.5 % 97.5 %
calc_agefirst -0.3375819 -0.232863
> # 이를 승비로 (odds ratio) 보면
> exp(confint(fit.ex6.3.centered)[2, , drop = F])
Waiting for profiling to be done...
2.5 % 97.5 %
calc_agefirst 0.7134935 0.7922621
>
해석: 처음 알콜경험한 나이와 마리화나 처음경험과는 음의 상관관계를 보였다 (OR = 0.753; 95% CI = 0.713, 0.792; p < .001). 개인의 알콜경험 나이가 한 살씩 많아질 때마다 (가령 18살에서 19살로), 마리화나의 처음경험은 24.7% 낮아지는 것으로 판단이 되었다.
IV increase not by one, but by many
- 처음 알콜 경험이 3년 늦춰지게 되면 $24.7\% * 3$ 인가?
- 그렇지 않고 처음 승비를 알려주는 b coefficient에서 (odds ratio = -0.2835)
- 3을 곱해준 후, 해당 OR을 구한다. 즉
- $e^{-0.2835*3}$
- 아래처럼 약 42.71% 이므로
- 3년 터울로 보면 약 (100-42.71% = 57.29%) 마리화나 처음경험의 odds를 갖는다고 하겠다
> #################################
> # 1년이 아니라 3년일 경우
> fit.ex6.3.centered
Call: glm(formula = mj_lifetime ~ calc_agefirst, family = binomial,
data = nsduh)
Coefficients:
(Intercept) calc_agefirst
0.5207 -0.2835
Degrees of Freedom: 842 Total (i.e. Null); 841 Residual
(157 observations deleted due to missingness)
Null Deviance: 1141
Residual Deviance: 968.4 AIC: 972.4
> coef(fit.ex6.3.centered)["calc_agefirst"]
calc_agefirst
-0.283531
> coef(fit.ex6.3.centered)["calc_agefirst"]*3
calc_agefirst
-0.850593
> exp(coef(fit.ex6.3.centered)["calc_agefirst"]*3)
calc_agefirst
0.4271616
>
CI는
> # CI 의 경우 아래와 같고
> confint(fit.ex6.3.centered)[2,]*3
Waiting for profiling to be done...
2.5 % 97.5 %
-1.012746 -0.698589
> # 이에 해당하는 값은
> exp(confint(fit.ex6.3.centered)[2,]*3)
Waiting for profiling to be done...
2.5 % 97.5 %
0.3632203 0.4972865
>
Multiple Regression
DV: lifetime marijuana use (mj_lifetime)
IVs:
- age at first use of alcohol (alc_agefirst),
- adjusted for age (demog_age_cat6),
- sex (demog_sex), and
- income (demog_income)
fit.ex6.3.adj <- glm(mj_lifetime ~ alc_agefirst + demog_age_cat6 + demog_sex +
demog_income, family = binomial, data = nsduh)
# Regression coefficient table
round(summary(fit.ex6.3.adj)$coef, 4)
> #################################
> #################################
> ## Multiple regression
> #################################
> fit.ex6.3.adj <- glm(mj_lifetime ~ alc_agefirst +
+ demog_age_cat6 + demog_sex +
+ demog_income,
+ family = binomial, data = nsduh)
> # Regression coefficient table
> round(summary(fit.ex6.3.adj)$coef, 4)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 6.2542 0.5914 10.5759 0.0000
alc_agefirst -0.2754 0.0276 -9.9922 0.0000
demog_age_cat626-34 -0.2962 0.3286 -0.9012 0.3675
demog_age_cat635-49 -0.8043 0.2966 -2.7120 0.0067
demog_age_cat650-64 -0.6899 0.2985 -2.3109 0.0208
demog_age_cat665+ -1.2748 0.3043 -4.1893 0.0000
demog_sexMale -0.0609 0.1618 -0.3763 0.7067
demog_income$20,000 - $49,999 -0.5309 0.2664 -1.9927 0.0463
demog_income$50,000 - $74,999 -0.0793 0.3049 -0.2601 0.7948
demog_income$75,000 or more -0.3612 0.2532 -1.4264 0.1538
>
# Regression coefficient table
round(summary(fit.ex6.3.adj)$coef, 4)
coef(fit.ex6.3.adj)
exp(coef(fit.ex6.3.adj))
col1 <- exp(coef(fit.ex6.3.adj))
confint(fit.ex6.3.adj)
exp(confint(fit.ex6.3.adj))
col2 <- exp(confint(fit.ex6.3.adj))
cbind("AdjOR" = col1, col2)[-1,]
round(cbind("AdjOR" = col1, col2)[-1,],3)
# OR은 coefficient 값을 이야기하는 것을 다시 확인
# 또한 Wald significant test 도 실행
car::Anova(fit.ex6.3.adj, type = 3, test.statistic = "Wald")
> # Regression coefficient table
> round(summary(fit.ex6.3.adj)$coef, 4)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 6.2542 0.5914 10.5759 0.0000
alc_agefirst -0.2754 0.0276 -9.9922 0.0000
demog_age_cat626-34 -0.2962 0.3286 -0.9012 0.3675
demog_age_cat635-49 -0.8043 0.2966 -2.7120 0.0067
demog_age_cat650-64 -0.6899 0.2985 -2.3109 0.0208
demog_age_cat665+ -1.2748 0.3043 -4.1893 0.0000
demog_sexMale -0.0609 0.1618 -0.3763 0.7067
demog_income$20,000 - $49,999 -0.5309 0.2664 -1.9927 0.0463
demog_income$50,000 - $74,999 -0.0793 0.3049 -0.2601 0.7948
demog_income$75,000 or more -0.3612 0.2532 -1.4264 0.1538
> coef(fit.ex6.3.adj)
(Intercept) alc_agefirst
6.25417324 -0.27541454
demog_age_cat626-34 demog_age_cat635-49
-0.29618703 -0.80427437
demog_age_cat650-64 demog_age_cat665+
-0.68990572 -1.27475385
demog_sexMale demog_income$20,000 - $49,999
-0.06088993 -0.53087558
demog_income$50,000 - $74,999 demog_income$75,000 or more
-0.07930897 -0.36119745
> exp(coef(fit.ex6.3.adj))
(Intercept) alc_agefirst
520.1791313 0.7592573
demog_age_cat626-34 demog_age_cat635-49
0.7436483 0.4474125
demog_age_cat650-64 demog_age_cat665+
0.5016234 0.2794998
demog_sexMale demog_income$20,000 - $49,999
0.9409268 0.5880898
demog_income$50,000 - $74,999 demog_income$75,000 or more
0.9237545 0.6968414
> col1 <- exp(coef(fit.ex6.3.adj))
> confint(fit.ex6.3.adj)
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) 5.1309585 7.45103372
alc_agefirst -0.3312435 -0.22314999
demog_age_cat626-34 -0.9490643 0.34307731
demog_age_cat635-49 -1.4002915 -0.23429671
demog_age_cat650-64 -1.2893673 -0.11559836
demog_age_cat665+ -1.8854986 -0.68944515
demog_sexMale -0.3790935 0.25566208
demog_income$20,000 - $49,999 -1.0591496 -0.01305382
demog_income$50,000 - $74,999 -0.6785210 0.51882750
demog_income$75,000 or more -0.8643471 0.13016735
> exp(confint(fit.ex6.3.adj))
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) 169.1792047 1721.6419228
alc_agefirst 0.7180303 0.7999949
demog_age_cat626-34 0.3871031 1.4092777
demog_age_cat635-49 0.2465251 0.7911270
demog_age_cat650-64 0.2754450 0.8908329
demog_age_cat665+ 0.1517534 0.5018544
demog_sexMale 0.6844816 1.2913163
demog_income$20,000 - $49,999 0.3467506 0.9870310
demog_income$50,000 - $74,999 0.5073668 1.6800566
demog_income$75,000 or more 0.4213265 1.1390190
> col2 <- exp(confint(fit.ex6.3.adj))
Waiting for profiling to be done...
> cbind("AdjOR" = col1, col2)[-1,]
AdjOR 2.5 % 97.5 %
alc_agefirst 0.7592573 0.7180303 0.7999949
demog_age_cat626-34 0.7436483 0.3871031 1.4092777
demog_age_cat635-49 0.4474125 0.2465251 0.7911270
demog_age_cat650-64 0.5016234 0.2754450 0.8908329
demog_age_cat665+ 0.2794998 0.1517534 0.5018544
demog_sexMale 0.9409268 0.6844816 1.2913163
demog_income$20,000 - $49,999 0.5880898 0.3467506 0.9870310
demog_income$50,000 - $74,999 0.9237545 0.5073668 1.6800566
demog_income$75,000 or more 0.6968414 0.4213265 1.1390190
> round(cbind("AdjOR" = col1, col2)[-1,],3)
AdjOR 2.5 % 97.5 %
alc_agefirst 0.759 0.718 0.800
demog_age_cat626-34 0.744 0.387 1.409
demog_age_cat635-49 0.447 0.247 0.791
demog_age_cat650-64 0.502 0.275 0.891
demog_age_cat665+ 0.279 0.152 0.502
demog_sexMale 0.941 0.684 1.291
demog_income$20,000 - $49,999 0.588 0.347 0.987
demog_income$50,000 - $74,999 0.924 0.507 1.680
demog_income$75,000 or more 0.697 0.421 1.139
>
> # OR은 coefficient 값을 이야기하는 것을 다시 확인
> # 또한 Wald significant test 도 실행
>
> car::Anova(fit.ex6.3.adj, type = 3, test.statistic = "Wald")
Analysis of Deviance Table (Type III tests)
Response: mj_lifetime
Df Chisq Pr(>Chisq)
(Intercept) 1 111.8504 < 2.2e-16 ***
alc_agefirst 1 99.8435 < 2.2e-16 ***
demog_age_cat6 4 23.0107 0.000126 ***
demog_sex 1 0.1416 0.706685
demog_income 3 5.4449 0.141974
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Interpretation of the output:
- The AOR for our primary predictor alc_agefirst is 0.759. This represents the OR for lifetime marijuana use comparing those with a one-year difference in age at first use of alcohol, adjusted for age, sex, and income.
- The remaining AORs compare levels of categorical predictors to their reference level, adjusted for the other predictors in the model.
- For example, comparing individuals with the same age of first alcohol use, sex, and income, 35-49 year-olds have 55.3% lower odds of lifetime marijuana use than 18-25 year-olds (OR = 0.447; 95% CI = 0.247, 0.791; p = .007).
- The p-value for this specific comparison of ages comes from the coefficients table. An overall, 4 df p-value for age, can be read from the Type III Test table (0.00013).
- The Type III tests output contains the multiple df Wald tests for categorical predictors with more than two levels. For continuous predictors, or for categorical predictors with exactly two levels, the Type III Wald test p-values are identical to those in the Coefficients table.
Conclusion:
- After adjusting for age, sex, and income, age at first alcohol use is significantly negatively associated with lifetime marijuana use (AOR = 0.759; 95% CI = 0.718, 0.800; p < .001). Individuals who first used alcohol at a given age have 24.1% lower odds of having ever used marijuana than those who first used alcohol one year earlier.
e.g. 1
# install.packages("oddsratio")
# library(oddsratio)
fit_glm <- glm(admit ~ gre + gpa + rank, data = data_glm, family = "binomial")
summary(fit_glm)
# Calculate OR for specific increment step of continuous variable
or_glm(data = data_glm, model = fit_glm,
incr = list(gre = 40, gpa = .1))
e.g. 2
https://stats.idre.ucla.edu/r/dae/logit-regression/
mydata <- read.csv("https://stats.idre.ucla.edu/stat/data/binary.csv")
## view the first few rows of the data
head(mydata)
admit gre gpa rank 1 0 380 3.61 3 2 1 660 3.67 3 3 1 800 4.00 1 4 1 640 3.19 4 5 0 520 2.93 4 6 1 760 3.00 2
summary(mydata)
admit gre gpa rank Min. :0.0000 Min. :220.0 Min. :2.260 Min. :1.000 1st Qu.:0.0000 1st Qu.:520.0 1st Qu.:3.130 1st Qu.:2.000 Median :0.0000 Median :580.0 Median :3.395 Median :2.000 Mean :0.3175 Mean :587.7 Mean :3.390 Mean :2.485 3rd Qu.:1.0000 3rd Qu.:660.0 3rd Qu.:3.670 3rd Qu.:3.000 Max. :1.0000 Max. :800.0 Max. :4.000 Max. :4.000
sapply(mydata, mean) sapply(mydata, sd)
> sapply(mydata, mean)
admit gre gpa rank
0.3175 587.7000 3.3899 2.4850
> sapply(mydata, sd)
admit gre gpa rank
0.4660867 115.5165364 0.3805668 0.9444602
>
xtabs(~admit + rank, data = mydata)
> xtabs(~admit + rank, data = mydata)
rank
admit 1 2 3 4
0 28 97 93 55
1 33 54 28 12
mydata$rank <- factor(mydata$rank) mylogit <- glm(admit ~ gre + gpa + rank, data = mydata, family = "binomial") summary(mylogit)
Call:
glm(formula = admit ~ gre + gpa + rank, family = "binomial",
data = mydata)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6268 -0.8662 -0.6388 1.1490 2.0790
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.989979 1.139951 -3.500 0.000465 ***
gre 0.002264 0.001094 2.070 0.038465 *
gpa 0.804038 0.331819 2.423 0.015388 *
rank2 -0.675443 0.316490 -2.134 0.032829 *
rank3 -1.340204 0.345306 -3.881 0.000104 ***
rank4 -1.551464 0.417832 -3.713 0.000205 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 499.98 on 399 degrees of freedom
Residual deviance: 458.52 on 394 degrees of freedom
AIC: 470.52
Number of Fisher Scoring iterations: 4
>
> confint(mylogit)
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) -6.2716202334 -1.792547080
gre 0.0001375921 0.004435874
gpa 0.1602959439 1.464142727
rank2 -1.3008888002 -0.056745722
rank3 -2.0276713127 -0.670372346
rank4 -2.4000265384 -0.753542605
>
> ## CIs using standard errors
> confint.default(mylogit)
2.5 % 97.5 %
(Intercept) -6.2242418514 -1.755716295
gre 0.0001202298 0.004408622
gpa 0.1536836760 1.454391423
rank2 -1.2957512650 -0.055134591
rank3 -2.0169920597 -0.663415773
rank4 -2.3703986294 -0.732528724
wald.test(b = coef(mylogit), Sigma = vcov(mylogit), Terms = 4:6)
l <- cbind(0, 0, 0, 1, -1, 0) wald.test(b = coef(mylogit), Sigma = vcov(mylogit), L = l)
관련 동영상
Logistic Regression Tutorial
\begin{align} y = b_{0} + b_{1}x \\ p = \frac{1} {1 + e^{-y}} \\ ln(\frac{p}{1-p}) = b_{0} + b_{1}x \\ \end{align}
Logistic Regression Details Pt1: Coefficients
Logistic Regression Details Pt 2: Maximum Likelihood
Logistic Regression Details Pt 3: R-squared and p-value