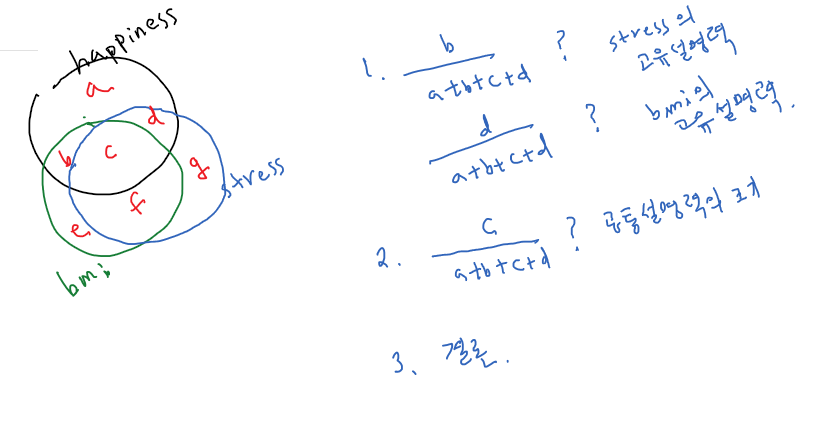Table of Contents
Discussion
Ex. 1
- Install packages ISLR
- use a dataset, Carseats
- Build regression models with a DV, sales and IVs, your choices
- Use
?Carseatscommand for the explanation of the dataset - Use
strfunction to see the characteristic of each variable. Make it sure thatSelvesLocvariable should be factor, not int or anything. - 변인설명을 토대로 가설만들기
- 종속변인 = Sales
- 독립변인 = 숫자변인 1 + 종류변인 1 (조별 선택)
- Multiple regression without interactin
- Multiple regression with interaction
- 가설 만들기
- 종속변인 Sales
- 독립변인 여러개 (interaction 없이)
- Modeling 해 볼 것
see hierarchical regression
see also statistical regression methods ← 많이 쓰이지 않음
Make a full model (with all variables) then reduce down the model until you find it fitted.Make a null model (with no variables) then, build up the model with additional IVs until you find a fitted model.Can we usesteporstepAIC(MASS package needed) function?Interpret the result
> step(lm.full, direction=“back”)
Ex. 2
- Install packages tidyverse
- load the tidyverse
install.packages("car")install.packages("carData")- load the car and the carData
data("Salaries", package = "carData")?Salaries- explain what it is
- describe the data set
—-
- Regress sex variable on salary variable
- Write the regression model
- Discuss the difference male and female (sex)
- Use rank variable for the same purpose
- Write the regression model
- Regress rank + sex on salary
- How do you interpret the result?
- And regress rank + sex + rank:sex on salary
- How do you interpret this result?
- Do factorial ANOVA test with rank and sex on salary
- How do you interpret the result?
- Test regression model of your own choice
- Interpret the result
위의 Salaries 데이터사용이 안 될 때
- download to R from here salaries.csv
- use to import the data set.
Salaries <- read.csv("http://commres.net/wiki/_media/salaries.csv")
- for information about Salaries (it may not be loaded),
- use
??Salariesto describe the data set.
—–
Please copy and paste the proper r command and output to a txt file (use notepad or some other text editing program). You could use MS Word, but, please make it sure that you use type-setting fonts such as “Courier New.” The below output, as an example, includes the r command head(Salaries) and the output.
Discussion 1
종속변인으로 salary 를 두고 소윤석 학생은 아래를 수행하였습니다.
>
> lm.sex <- lm(salary ~ sex, data = Salaries)
> summary(lm.sex)
Call:
lm(formula = salary ~ sex, data = Salaries)
Residuals:
Min 1Q Median 3Q Max
-57290 -23502 -6828 19710 116455
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 101002 4809 21.001 < 2e-16 ***
sexMale 14088 5065 2.782 0.00567 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 30030 on 395 degrees of freedom
Multiple R-squared: 0.01921, Adjusted R-squared: 0.01673
F-statistic: 7.738 on 1 and 395 DF, p-value: 0.005667
윤석학생은 테스트 결과를 보고 교수의 salary에 대한 sex의 설명력이 약 1.9% 이며, 이 때의 F-test 값은 F(1, 395) = 7.738, p < 0.005667 이었다고 기록 한 후, 이에 따라서 교수들의 salary에 대해 sex는 통계학적으로 유의미한 (significant) 기여를 한다고 판단하였습니다. 특히 에는 female일 경우 101002 달러인 것에 반해 male일 경우에는 115090 달러의 연봉을 받는다고 판단하였습니다.
윤석학생은 여기에 더하여 다른 독립변인님 rank를 추가해 보기로 하였습니다. 결과는 아래와 같았습니다.
> lm.sexRank <- lm(salary ~ sex + rank, data = Salaries)
> summary(lm.sexRank)
Call:
lm(formula = salary ~ sex + rank, data = Salaries)
Residuals:
Min 1Q Median 3Q Max
-69307 -15757 -1449 12359 104438
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 76645 4433 17.290 < 2e-16 ***
sexMale 4943 4026 1.228 0.22029
rankAssocProf 13061 4128 3.164 0.00168 **
rankProf 45519 3252 13.998 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 23620 on 393 degrees of freedom
Multiple R-squared: 0.3966, Adjusted R-squared: 0.392
F-statistic: 86.09 on 3 and 393 DF, p-value: < 2.2e-16
윤석학생은 이 결과를 보고 즉시, R 제곱값이 39.66% 가 되었음을 보고 고무되었습니다. 두 독립변인의 설명력이 (둘을 합쳐) 39.66% 인 것은 이전의 sex만의 1.9%인가 되는 설명력에 비해 상당히 많아진 결과입니다. 당연히 이 모델은 (테스트 결과는) 통계학적으로 유의미하였습니다 (F(3, 393) = 86.09, p < 0.0001).
그러나, 윤석학생은 이전에 독립적으로 사용하였던 sex의 설명력이 사라진 것을 알게 되었습니다 (p 0.22029). 윤석학생은 그러나, 이전의 결과에 비추어 어떻게 이 결과를 어떻게 해석해야 할 지 막막하다는 생각을 합니다. 만약에 두 번째 분석만을 했었더라면 sex 변인은 미국 교수들의 salary를 설명하는데에 큰 기여를 하지 않는다고 판단을 하겠지만, 윤석학생은 sex만을 가지고 분석을 했었을 경우에의 설명력을 그냥 무시할 수는 없다고 생각합니다. 이것에 대해서 윤석학생은 클래스의 다른 학생들과 토론하고 싶어 합니다.
Discussion 2
Carseats 데이터에 대한 것이다. Sales 를 dependent variable 로 하고 데이터 내의 다른 변인을 IV로 한다고 생각할 때, 어떤 것을 포함 시켜야 Carseats 판매를 가장 잘 설명하는 것이 될까? (Carseats sale을 가장 잘 설명하는 모델)
cor
spcor
pcor
영향력 가장 큰 순서 . . . .
독립변인 성격에 따라서 독립변인을 묶어서 (sequential)
예
- 우선 str(Carseats) 를 이용해서 데이터를 살펴보면 11개의 변인이 있음을 알 수 있고, 종속변인으로 Sales를 두고 Sales를 설명하는 변인으로 어떤 것을 취해야 하는가를 생각해 본다.
- 변인들을 그냥 눈으로 (이론과 상시적으로) 살펴보면 크게 아래와 같이 나누어 진다
- Price, CompPrice 는 carseats의 가격과 관련된 변인으로 상품의 가격이 sales에 영향을 준다는 것이다
- Advertising은 인지도 혹은 인지력과 관련해서 사람들이 상품에 대해서 얼마나 알고 있게 되는가에 대한 변인이니 또 다른 종류의 변인이라고 생각할 수 있다.
- 이 외의 변인들을 보면 가게가 있는 지역의 인구통계학적인 특징으로 볼 수 있다 (income, population, education, 등등)
- 이렇게 3 종류의 변인이 독립변인군으로 남는 것 외에
- ShelveLoc은 상품을 사려고 하는 사람에게 직접적으로 영향을 주는 특별한 변인으로 볼 수 있다.
- 따라서 이론적으로 연구자는 Price관련, Ads관련, 인구통계학관련 변인과 상품진열관련 변인이 세일즈에 영향을 준다고 파악하는 것이 어느정도 합리적이라고 본다.
- 이에 따라서 분석을 하기로 한다.
# install.packages("ISLR")
library(ISLR)
head(Carseats)
str(Carseats)
cor(Carseats)
cs.num <- Carseats[, c(1:6, 8, 9)]
str(cs.num)
head(cs.num)
cor(cs.num)
# install.packages(ppcor)
# for partial and semipartial (part) correlation
# library(ppcor)
spcor(cs.num)
round(spcor(cs.num)$estimate,2)
round(cor(cs.num),2)
# regression analsys 시작
# 우선 price관련 독립변인
lm.price <- lm(Sales ~ Price + CompPrice, data = cs.num)
summary(lm.price)
# 다음으로 인지도 (Advertising)
lm.price.ads <- lm(Sales ~ Price + CompPrice + Advertising, data = cs.num)
summary(lm.price.ads)
# 다음으로 인구통계학적 특징
lm.price.ads.pop <- lm(Sales ~ Price + compPrice +
Advertising +
Income + Population + Age + Education,
data=cs.num)
summary(lm.price.ads.pop)
# Population, Education out
lm.price.ads.pop2 <- lm(Sales ~ Price + compPrice +
Advertising +
Income + Age,
data=cs.num)
summary(lm.price.ads.pop2)
# ShelveLoc 을 더해 본다
lm.price.ads.pop2.sh <- lm(Sales ~ Price + compPrice
+ Advertising
+ Income + Age
+ ShelveLoc,
data=Carseats)
summary(lm.price.ads.pop2.sh)
# interaction check
# 이론적으로 그리고 상식적으로 Ads와 진열위치가 상호작용할 수
# 있을 듯 하다
lm.price.ads.pop2.sh.ia <- lm(Sales ~ Price + CompPrice
+ Advertising
+ Income + Age
+ ShelveLoc
+ Advertising:ShelveLoc,
data=Carseats)
summary(lm.price.ads.pop2.sh.ia)
# 독립변인 추가 때 마다 R 제곱값이 통계학적으로 유의미하게 바뀌었는가?
anova(lm.price, lm.price.ads)
anova(lm.price.ads, lm.price.ads.pop2)
anova(lm.price.ads.pop2, lm.price.ads.pop2.sh)
# r square value 차이
# 참고로 names(summary(lm.price.ads)) 를 치면
# summary(model)의 개체가 갖는 리스트항목들이 출력이 됨
# 그 중의 하나가 r.squared
summary(lm.price.ads)$r.squared - summary(lm.price)$r.squared
summary(lm.price.ads.pop2)$r.squared - summary(lm.price.ads)$r.squared
summary(lm.price.ads.pop2.sh)$r.squared - summary(lm.price.ads.pop2)$r.squared
# 위의 r squared value 차이는 모두 통계학적으로 의미있음, anova 테스트로 확인했음
# 참고로 인터액션이 어떤 작용을 하는지 보기 위해서 Advertising을 제외하고
# Advertising:ShelveLoc 을 추가해서 본다
lm.price.pop2.sh.ia <- lm(Sales ~ Price + CompPrice
+ Income + Age
+ ShelveLoc
+ Advertising:ShelveLoc,
data=Carseats)
summary(lm.price.pop2.sh.ia)
마지막 분석은 Advertising의 주효과를 제외하고 이 변인과 ShelveLoc간의 interaction이 어떻게 전개되는가를 보기위한 궁금증 해소차원의 분석으로
> lm.price.pop2.sh.ia <- lm(Sales ~ Price + CompPrice
+ + Income + Age
+ + ShelveLoc
+ + Advertising:ShelveLoc,
+ data=Carseats)
> summary(lm.price.pop2.sh.ia)
Call:
lm(formula = Sales ~ Price + CompPrice + Income + Age + ShelveLoc +
Advertising:ShelveLoc, data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-2.8255 -0.7178 0.0430 0.6725 3.2973
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.396938 0.513377 10.513 < 2e-16 ***
Price -0.095392 0.002673 -35.685 < 2e-16 ***
CompPrice 0.092950 0.004137 22.468 < 2e-16 ***
Income 0.015786 0.001840 8.580 2.27e-16 ***
Age -0.046453 0.003191 -14.559 < 2e-16 ***
ShelveLocGood 4.800421 0.218742 21.946 < 2e-16 ***
ShelveLocMedium 2.065332 0.175114 11.794 < 2e-16 ***
ShelveLocBad:Advertising 0.124994 0.016296 7.670 1.39e-13 ***
ShelveLocGood:Advertising 0.128358 0.016401 7.826 4.78e-14 ***
ShelveLocMedium:Advertising 0.107273 0.010383 10.331 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.02 on 390 degrees of freedom
Multiple R-squared: 0.8725, Adjusted R-squared: 0.8696
F-statistic: 296.5 on 9 and 390 DF, p-value: < 2.2e-16
>
위에서 마지막 세줄을 보면
ShelveLocBad:Advertising 0.124994 0.016296 7.670 1.39e-13 *** ShelveLocGood:Advertising 0.128358 0.016401 7.826 4.78e-14 *** ShelveLocMedium:Advertising 0.107273 0.010383 10.331 < 2e-16 ***
Advertising의 값이 ShelveLocGood 일적에는 0.128358 증가하고
ShelveLocMedium 일때는 0.107273, 그리고
ShelveLocBad 일 때는 0.124994 으로 증가한다는 것을 보여주는데 세 조건에서 거의 비슷하게 진행됨을 알 수 있으며
이는 interaction effect는 없음을 보여주는 것이다.
interaction effect가 있는 것처럼 나타나는 이유는
각각의 기울기가 Advertising의 주효과를 포함하고 있기 때문으로 생각된다.
추가설명
명지학생을 위해서 조금 더 설명할께요.
주효과를 없애고 인터액션을 보는 경우는 흔치 않습니다.
mod.1 <- lm(y ~ x1 + x1:x2, data=md)
를 한다고 할 때 x1과 x2 모두가 종류변인일 경우에는 main effect를 제외하고 볼 수는 없습니다.
x1, x2가 모두 숫자변인이거나, 둘 중에 하나가 숫자, 다른하나가 종류 일 때는 가능하겠습니다. 우리 예의 모델이 독립변인이 많아서 좀 복잡하므로 이를 줄여서 간단히 보면 아래와 같은 모델을 취하는 것이라 하겠습니다.
아래는 Advertising을 없애질 않고 ShelveLoc을 없앤것이라서 약간 다르게 보이지만 요지는 같습니다.
> lm.1 <- lm(Sales ~ Advertising + Advertising:ShelveLoc, data = Carseats)
> summary(lm.1)
Call:
lm(formula = Sales ~ Advertising + Advertising:ShelveLoc, data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-6.7650 -1.7351 -0.1523 1.5481 8.1350
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.76500 0.17503 38.650 < 2e-16 ***
Advertising -0.05412 0.03136 -1.726 0.0852 .
Advertising:ShelveLocGood 0.35597 0.03901 9.126 < 2e-16 ***
Advertising:ShelveLocMedium 0.14922 0.03346 4.460 1.07e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.476 on 396 degrees of freedom
Multiple R-squared: 0.237, Adjusted R-squared: 0.2312
F-statistic: 41 on 3 and 396 DF, p-value: < 2.2e-16
>
위에서 prediction model 식을 완성한다고 하면
- Sales hat = 6.76500 - 0.05412 * Advertising –> ShelveLocBad 인경우
- Sales hat = 6.76500 + (-0.05412 + 0.14922) * Advertising –> ShelveLocMedium 인경우
- Sales hat = 6.76500 - (0.0951)*Advertising –> ShelveLocMedium 인경우
- Sales hat = 6.76500 + (-0.05412 + 0.35597) * Advertising –> ShelveLocGood 인경우
- Sales hat = 6.76500 - (0.30185)*Advertising –> ShelveLocGood 인경우
라고 하겠습니다.
기울기가 변하는 거죠. 이를 그래프로 그려보겠습니다.
> plot(Advertising, Sales)
위의 plot 명령어는 fansy한 옵션을 쓰지는 않지만 그래프는 나타내 줍니다. 아래와 같습니다.
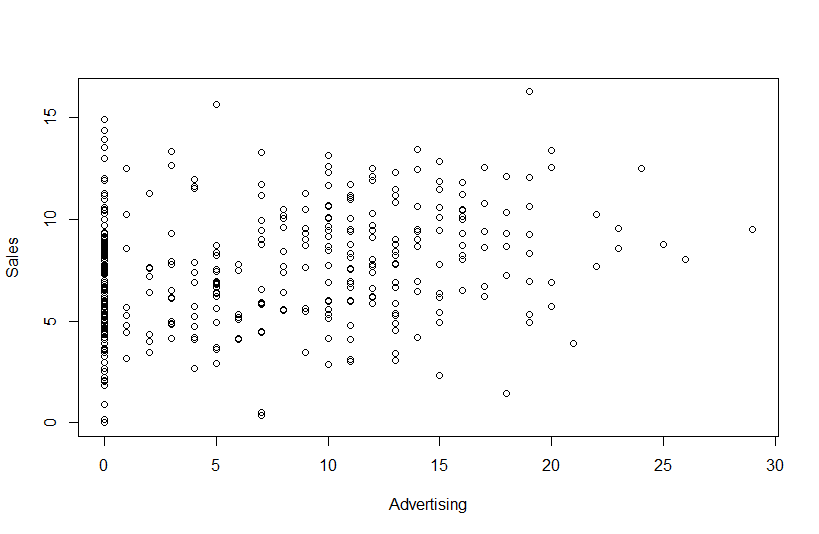
이 데이터에서 각각의 Sales hat 에 대한 기울기 선을 그리려고 하면 아래와 같이 abline add-명령어를 써줍니다. 아웃풋은 아래와 같습니다.
> abline(a = 6.76500, b = 0.30185, col = "green", lwd=3) # ShelveLoc Good 인경우 > abline(a = 6.76500, b = 0.0951, col = "red", lwd=3) # Medium 인 경우 > abline(a = 6.76500, b = -0.05412, col = "blue", lwd=3) # Bad 인 경우
- 녹색선은 ShelveLoc 이 Good 일 때의 Advertising과 Sales 관계를 보여줍니다.
- 빨간선은 ShelveLoc 이 Medium 일 때의 Advertising과 Sales 관계를 보여줍니다.
- 파란선은 ShelveLoc 이 Bad 일 때의 Advertising과 Sales 관계를 보여줍니다.
이를 풀어서 이야기하자면
- 광고를 해서 많이 알려진 상품을 좋은 곳에 진열하면 더 잘 팔리고
- 광고를 해서 잘 알려진 상품을 중간장소에 진열하면 팔리는 양이 좋은 곳 진열했을 때 보다 약간 떨어지고
- 가장 않좋은 장소 진열한 상품이 가장 판매가 떨어진다는 이야기입니다.
인터액션이 있는 것처럼 해석이 되죠. 그런데, 위의 이야기는
ShelveLoc을 Main effect를 보기 위해서 독립변인으로 넣었을 때,
장소에 따라서 상품의 판매가 달라진다는 것과 다를게 없습니다. 바로 이것때문에
> lm.adsShelve <- lm(Sales ~ Advertising + ShelveLoc + Advertising:ShelveLoc, data = Carseats)
의 결과가 Advertising과 ShelveLoc의 설명력만 있고 interaction은 없다고 나타나는 이윱니다 (아래 아웃풋).
> lm.adsShelve <- lm(Sales ~ Advertising + ShelveLoc + Advertising:ShelveLoc, data = Carseats)
> summary(lm.adsShelve)
Call:
lm(formula = Sales ~ Advertising + ShelveLoc + Advertising:ShelveLoc,
data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-6.6074 -1.6079 -0.0678 1.5666 6.4318
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.01234 0.31932 15.697 < 2e-16 ***
Advertising 0.08210 0.03570 2.300 0.022 *
ShelveLocGood 4.43573 0.48146 9.213 < 2e-16 ***
ShelveLocMedium 1.59511 0.38378 4.156 3.97e-05 ***
Advertising:ShelveLocGood 0.02206 0.05075 0.435 0.664
Advertising:ShelveLocMedium 0.02482 0.04236 0.586 0.558
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.249 on 394 degrees of freedom
Multiple R-squared: 0.3738, Adjusted R-squared: 0.3659
F-statistic: 47.05 on 5 and 394 DF, p-value: < 2.2e-16
>
그리고 이렇게 해서 interaction effect는 없다고 보는 것이 맞지만, 선생님이 ShelveLoc이 Advertising과 어떤 관계로 나타나는지 살펴보기 위해서 temporary하게 ShelveLoc 의 main effect를 제외하고 (즉, regression에서 독립변인으로 제외하고), interaction temer만을 (Advertising:ShelveLoc) 추가해본겁니다. 그러면 패턴이 보이니까요. 즉, 광고효과는 진열과 상호작용해서 Sales로 나타난다고 생각해도 된다고 이야기해보려고 한것입니다.
아래는 설명을 하지 않고 코드만 적었었는데 이는 아래 둘의 model이 동일한 것임을 보여주기 위한 것입니다.
lm.2 <- lm(Sales ~ Advertising:ShelveLoc, data = Carseats) # ------- (1) lm.1 <- lm(Sales ~ Advertising + Advertising:ShelveLoc, data = Carseats) # ------- (2)
왜 같은지를 보기 위해서 아래를 보면
> lm.2 <- lm(Sales ~ Advertising:ShelveLoc, data = Carseats) # ------- (1)
> lm.1 <- lm(Sales ~ Advertising + Advertising:ShelveLoc, data = Carseats) # ------- (2)
> summary(lm.2)
Call:
lm(formula = Sales ~ Advertising:ShelveLoc, data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-6.7650 -1.7351 -0.1523 1.5481 8.1350
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.76500 0.17503 38.650 < 2e-16 ***
Advertising:ShelveLocBad -0.05412 0.03136 -1.726 0.0852 .
Advertising:ShelveLocGood 0.30185 0.02982 10.123 < 2e-16 ***
Advertising:ShelveLocMedium 0.09510 0.02222 4.281 2.34e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.476 on 396 degrees of freedom
Multiple R-squared: 0.237, Adjusted R-squared: 0.2312
F-statistic: 41 on 3 and 396 DF, p-value: < 2.2e-16
1) Bad 인 경우는
- Sales hat = 6.76500 + -0.05412*Advertising 이 됩니다.
2) ShelveLoc Good일 경우, ShelveLOcGood = 1이고 나머지는 0이므로
- Sales hat = Intercept + Advertising:ShelveLocGood 이 됩니다. 즉,
- Sales hat = 6.76500 + 0.30185*Advertising
- 위의 * Advertising은
- Advertising:ShelveLocGood 에서
- Ad coefficient (0.30185) * SelfveLocGood (1) 이라는 이야기입니다.
3) ShelveLoc Medium일 경우는
- Sales hat = 6.76500 + 0.09510 * Advertising 이 됩니다
위는 결국 lm.1 과 같은 모델이라는 뜻입니다.
참고로 위에서 원래 lm.1에서 우리가 살펴본 각 라인은 아래와 같았었습니다.
> abline(a = 6.76500, b = 0.30185, col = "green", lwd=3) # ShelveLoc Good 인경우 > abline(a = 6.76500, b = 0.0951, col = "red", lwd=3) # Medium 인 경우 > abline(a = 6.76500, b = -0.05412, col = "blue", lwd=3) # Bad 인 경우
추가 설명 2
선생님이 처음 예에서는 Advertising을 빼고 interaction을 보고는 바로 위의 설명에서는 ShelveLoc을 빼서 (깜박하고 거꾸로 뺏어요) 좀 당황할 수 있으므로 원래대로 해도 마찬가지라는 걸 조금 보려고 합니다. 이것을 R code로 쓰면 아래와 같습니다. 처음것은 두변인과 두변인의 interaction을 모두 포함한 것이고 그 다음 것은 Advertising 주효과를 제외한 것입니다.
> lm.adsShelve <- lm(Sales ~ Advertising + ShelveLoc + Advertising:ShelveLoc, data = Carseats)
> summary(lm.adsShelve)
Call:
lm(formula = Sales ~ Advertising + ShelveLoc + Advertising:ShelveLoc,
data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-6.6074 -1.6079 -0.0678 1.5666 6.4318
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.01234 0.31932 15.697 < 2e-16 *** # (1)
Advertising 0.08210 0.03570 2.300 0.022 * # (2)
ShelveLocGood 4.43573 0.48146 9.213 < 2e-16 *** # (3)
ShelveLocMedium 1.59511 0.38378 4.156 3.97e-05 *** # (4)
Advertising:ShelveLocGood 0.02206 0.05075 0.435 0.664 # (5)
Advertising:ShelveLocMedium 0.02482 0.04236 0.586 0.558 # (6)
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.249 on 394 degrees of freedom
Multiple R-squared: 0.3738, Adjusted R-squared: 0.3659
F-statistic: 47.05 on 5 and 394 DF, p-value: < 2.2e-16
ShelveLocBad case
- (1) = intercept, 5.01234
- (2) = Advertising, 0.08210*Advertising
- (3) = 0
- (4) = 0
- (5) = Advertising * 0
- (6) = Advertising * 0
- y.hat = 5.01234 + (0.08210)*advertising
Good case
- (1) = intercept, 5.01234
- (2) = Advertising, 0.08210*Advertising
- (3) = 4.43573
- (4) = 0
- (5) = Advertising * 1 = 0.02206
- (6) = Advertising * 0 = 0
- y.hat = 5.01234 + (0.08210)*Advertising + 4.43573 + (0.02206)*Advertising
- y.hat = 9.44807 + 0.10416*Advertising
Med case
- (1) = intercept, 5.01234
- (2) = Advertising, 0.08210*Advertising
- (3) = 0
- (4) = 1.59511
- (5) = Advertising * 0 = 0
- (6) = Advertising * 0.02482 = 0.02482*Advertising
- y.hat = 5.01234 + (0.08210)*Advertising + 1.59511 + (0.02482)*Advertising
- y.hat = 6.60745 + 0.10692*Advertising
> lm.5 <- lm(Sales ~ ShelveLoc + Advertising:ShelveLoc, data = Carseats)
> summary(lm.5)
Call:
lm(formula = Sales ~ ShelveLoc + Advertising:ShelveLoc, data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-6.6074 -1.6079 -0.0678 1.5666 6.4318
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.01234 0.31932 15.697 < 2e-16 *** # (1)
ShelveLocGood 4.43573 0.48146 9.213 < 2e-16 *** # (2)
ShelveLocMedium 1.59511 0.38378 4.156 3.97e-05 *** # (3)
ShelveLocBad:Advertising 0.08210 0.03570 2.300 0.02198 * # (4)
ShelveLocGood:Advertising 0.10417 0.03607 2.888 0.00409 ** # (5)
ShelveLocMedium:Advertising 0.10692 0.02280 4.689 3.78e-06 *** # (6)
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.249 on 394 degrees of freedom
Multiple R-squared: 0.3738, Adjusted R-squared: 0.3659
F-statistic: 47.05 on 5 and 394 DF, p-value: < 2.2e-16
위의 결과를 보면 (번호 (1)에서 (6)까지)
(1) = 5.01234
(2) = 0
(3) = 0
(4) = 0.08210 * (1 = location bad case) * Advertising
(5) = 0.10417 * (0 = location good case) * Advertising = 0
(6) = 0.10692 * (0 = location med case) * Advertising = 0
따라서,
Sales hat = 5.01234 + 0.08210 * Advertising
이 첫번째 경우가
- ShelveBad일 경우 intercept만 남고 (5.01234) (1)
- ShelveBad 가 1이고 나머지는 (Medium 과 Good) 0으로 보는 것이기에
- ShelveLocBad:Advertising (4)만 남고 아래 두 줄은 1) 0으로 없어지므로
- (1)에다 (4)의 0.08210*Advertising 이 더해져서
- y.hat = 5.01234 + 0.08210*Advertising
두번째 Good일 경우는
- Sales hat = (5.01234 + 4.43573) 이고 여기에 Advertising의 interaction을 고려하면
- Sales hat = (5.01234 + 4.43573) + 0.10417 * Advertising 이 됩니다.
- y.hat = 9.44807 + 0.10417 * Advertising
세번째 Medium일 경우는
- 5.01234에 (1) 1.59511을 (3) 더한 것이 ShleveLoc Medium 의 효과로
- Sales hat = (5.01234 + 1.59511) 이고 여기에 Advertising의 interaction을 고려하면 여기에 (6)을 고려해서
- Sales hat = (5.01234 + 1.59511) + 0.10692 * Advertising 이 되겠습니다.
- y.hat = 6.60745 + 0.10692*Advertising
그런데 Advertising 과의 상호작용 때문에 증가하는 양이 비슷비슷합니다. 이것을 그래프로 그리면
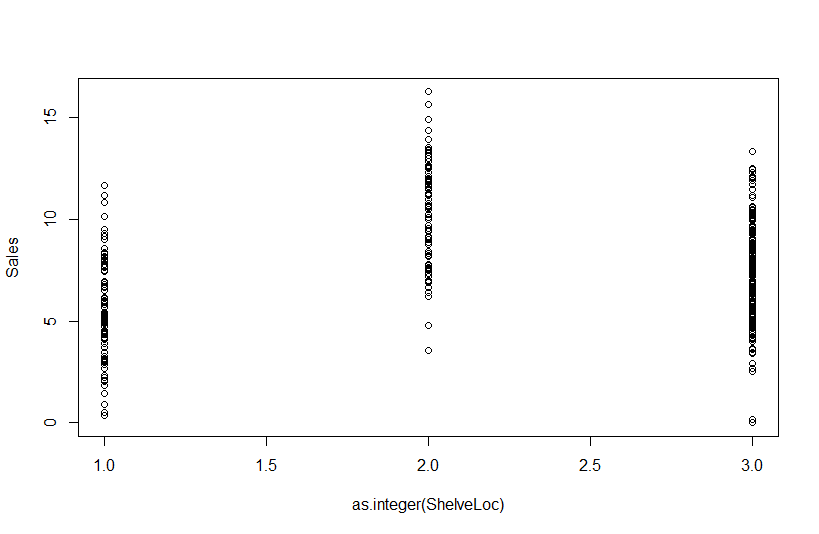
> plot(ShelveLoc, Sales)
 인데 이것은 scatter plot이 아니므로 편법을 써서 (ㅎㅎ, 12조 학생들이 이와 비슷한 아웃풋을 사용했습니다)
인데 이것은 scatter plot이 아니므로 편법을 써서 (ㅎㅎ, 12조 학생들이 이와 비슷한 아웃풋을 사용했습니다)
> plot(as.integer(ShelveLoc), Sales) # ShelveLoc 1, 2, 3을 factor에서 integer로 취급해달라고 합니다
위에서 가운데가 Good이고 오른 쪽이 Medium 왼쪽이 Bad입니다.
여기에 Advertising의 interaction 이펙트를 더하면 왼쪽부터 각 개인의 점수가
모두 0.08210 씩, 0.10417 씩, 그리고 0.10692씩 올라가게 된다는 겁니다.
그러니 이렇게 보아도 마찬가지임을 알 수 있죠?
개인과제 1
d.yyk <- read.csv("http://commres.net/wiki/_media/d.yyk.csv")
d.yyk
d.yyk <- subset(d.yyk, select = -c(1))
d.yyk
> d.yyk <- subset(d.yyk, select = -c(1))
> d.yyk
bmi stress happiness
1 15.1 2 4
2 15.3 2 4
3 16.4 1 5
4 16.3 2 4
5 17.5 2 3
6 18.8 2 4
7 19.2 2 3
8 20.3 1 4
9 21.3 1 4
10 21.3 2 4
11 22.4 2 5
12 23.5 2 5
13 23.7 2 4
14 24.2 3 3
15 24.3 3 3
16 25.6 2 3
17 26.4 3 3
18 26.4 3 2
19 26.4 3 2
20 27.5 3 3
21 28.6 3 2
22 28.2 4 2
23 31.3 3 2
24 32.1 4 1
25 33.1 4 1
26 33.2 5 1
27 34.4 5 1
28 35.8 5 1
29 36.1 5 1
30 38.1 5 1
우선 여기에서 종속변인인 (dv) happiness에 bmi와 stress를 리그레션 해본다.
attach(d.yyk) lm.happiness.bmistress <- lm(happiness ~ bmi + stress, data=d.yyk) summary(lm.happiness.bmistress) anova(lm.happiness.bmistress)
> attach(d.yyk)
> lm.happiness.bmistress <- lm(happiness ~ bmi + stress, data=d.yyk)
> summary(lm.happiness.bmistress)
Call:
lm(formula = happiness ~ bmi + stress, data = d.yyk)
Residuals:
Min 1Q Median 3Q Max
-0.89293 -0.40909 0.08816 0.29844 1.46429
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.29098 0.50779 12.389 1.19e-12 ***
bmi -0.05954 0.03626 -1.642 0.11222
stress -0.67809 0.19273 -3.518 0.00156 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5869 on 27 degrees of freedom
Multiple R-squared: 0.8217, Adjusted R-squared: 0.8085
F-statistic: 62.22 on 2 and 27 DF, p-value: 7.76e-11
>
>
> anova(lm.happiness.bmistress)
Analysis of Variance Table
Response: happiness
Df Sum Sq Mean Sq F value Pr(>F)
bmi 1 38.603 38.603 112.070 4.124e-11 ***
stress 1 4.264 4.264 12.378 0.001558 **
Residuals 27 9.300 0.344
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
위의 분석을 보면
R2 = 0.8217, F (2, 27) = 62.77, p = 7.76e-11
그러나, coefficient 값을 보면 bmi는 significant 하지 않고, stress는 significant하다. 이는 R제곱에 영향을 주는 것으로 stress가 주이고 bmi의 영향력은 미미하다고 하다는 결론을 내리도록 해준다. 그러나, multiple regression에서 언급한 것처럼 독립변인이 두 개 이상일 때에는 무엇이 얼마나 종속변인에 영향을 주는지 그림을 그릴 수 있어야 하므로, 아래와 같이 bmi만을 가지고 regression을 다시 해본다.
lm.happiness.bmi <- lm(happiness ~ bmi, data=d.yyk) summary(lm.happiness.bmi) anova(lm.happiness.bmi)
> lm.happiness.bmi <- lm(happiness ~ bmi, data=d.yyk)
>
> summary(lm.happiness.bmi)
Call:
lm(formula = happiness ~ bmi, data = d.yyk)
Residuals:
Min 1Q Median 3Q Max
-1.20754 -0.49871 -0.03181 0.35669 1.83265
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.24143 0.50990 14.202 2.54e-14 ***
bmi -0.17337 0.01942 -8.927 1.11e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.696 on 28 degrees of freedom
Multiple R-squared: 0.74, Adjusted R-squared: 0.7307
F-statistic: 79.69 on 1 and 28 DF, p-value: 1.109e-09
> anova(lm.happiness.bmi)
Analysis of Variance Table
Response: happiness
Df Sum Sq Mean Sq F value Pr(>F)
bmi 1 38.603 38.603 79.687 1.109e-09 ***
Residuals 28 13.564 0.484
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
놀랍게도 bmi 하나만을 가지고 regression을 했더니, R제곱 값이 .74이었다 (F(1,28) = 79.69, p = 1.109e-09). 이런 결과가 나올 수 있는 이유는 독립변인인 bmi와 stress 간의 상관관계가 높아서 처음 분석에서 그 영향력을 (설명력, R제곱에 기여하는 부분을) 하나의 독립변인이 모두 가졌갔기 때문이라고 생각할 수 있다. 이 경우에는 그 독립변인이 stress이다.
happiness에 stress 만을 regression 해본 결과는 아래와 같다.
lm.happiness.stress <- lm(happiness ~ stress, data = d.yyk) summary(lm.happiness.stress) anova(lm.happiness.stress)
> lm.happiness.stress <- lm(happiness ~ stress, data = d.yyk)
> summary(lm.happiness.stress)
Call:
lm(formula = happiness ~ stress, data = d.yyk)
Residuals:
Min 1Q Median 3Q Max
-0.7449 -0.6657 0.2155 0.3343 1.3343
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.58651 0.27965 19.98 < 2e-16 ***
stress -0.96041 0.08964 -10.71 2.05e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.6044 on 28 degrees of freedom
Multiple R-squared: 0.8039, Adjusted R-squared: 0.7969
F-statistic: 114.8 on 1 and 28 DF, p-value: 2.053e-11
> anova(lm.happiness.stress)
Analysis of Variance Table
Response: happiness
Df Sum Sq Mean Sq F value Pr(>F)
stress 1 41.938 41.938 114.8 2.053e-11 ***
Residuals 28 10.229 0.365
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
>
R제곱값은 0.80로 (F(1, 28) = 114.8, 2.053e-11) 스트레스만으로도 significant한 결과를 갖는다.
그렇다면 stress 와 bmi가 공통으로 기여하는 부분을 뺀 순수 기여분은 어떻게 될까? 즉, 위의 .80 부분 중 bmi와 공통으로 기여하는 부분을 제외한 나머지는 얼마일까? 보통 이와 같은 작업을 bmi의 (다른 독립변인의) 영향력을 제어하고 (control) 순수기여분만을 살펴본다고 이야기 한다.
이를 위해서 아래를 계획, 수행해본다.
- 각각의 독립변인이 고유하게 미치는 영향력은 (설명력은) 무엇인지를 본다.
- 공통설명력은 얼마나 되는지 본다.
- 1을 위해서는 각 독립변인과 종속변인인 happiness의 semi-partial correlation값을 구해서 제곱해보면 되겠다.
- 2를 위해서는 두 독립변인을 써서 구했던 r 제곱값에서 위의 1에서 구한 제곱값들을 제외한 나머지를 보면 된겠다.
- 결론을 내기 위한 계획을 세우고 실행한다.
- 이는 아래와 같이 정리할 수 있다
개인과제 2
Carseat에서 아주 이상한 일이 있습니다. 이것에 대해서 각 개인의 생각을 묻습니다.
# 개인과제와 관련된 코드입니다.
# Carseats 데이터 분석입니다. 새로 시작하면
library(ISLR)
# 만약에 ISLR이 install도 안되어
# 있으면
# install.packages("ISLR")
?Carseats # 데이터 설명 확인
str(Carseats)
# 이 중에서 CompPrice의 독립변인으로서의
# 역할에 문제점이 보이는 듯 하여 물어봅니다
# CompPrice와 다른 변인들을 모두 활용해도
# 되겠지만 간단하게 보기 위해서 Price만을
# 독립변인으로 분석을 합니다
lm.c1 <- lm(Sales ~ Price + CompPrice, data = Carseats)
summary(lm.c1)
# output 을 살펴보면 R 제곱값이
# 0.3578 (35.78%) 임을 알 수 있습니다.
# 이는 우리가 흔히 쓰는 다이어그램에서
#
# http://commres.net/wiki/_detail/pasted/20201201-170048.png?id=multiple_regression_exercise
#
# b + c + d 에 해당하는 부분입니다. 즉 두 변인의
# 설명력을 보여주는 부분인 lm.c1에서의
# R 제곱은 b + c + d / a + b + c + d 입니다.
# 여기에서 아래를 수행하여
# semipartial corrleation 값과 이를
# 제곱한 값을 알아봅니다.
library(ppcor)
attach(Carseats)
spcor.Price <- spcor.test(Sales, Price, CompPrice)
spcor.CompPrice <- spcor.test(Sales, CompPrice, Price)
spcor.Price
spcor.CompPrice
# 위 둘의 아웃풋에서 estimate값은
# semipartial correlation 값이므로 이를
# 제곱한 값은 각각 b와 d에 해당하는
# 값입니다. 이를 더 자세히 이야기하면
# b = b / a + b + c + d
# d = d / a + b + c + d
# 라는 이야기입니다.
b <- spcor.Price$estimate^2
d <- spcor.CompPrice$estimate^2
# 각 b와 d를 출력해 봅니다.
b
d
# 이 둘을 더해봅니다.
# 이 값은 0.5135791 입니다
b + d
# 다시 아까 lm.c1의 R 제곱값은
summary(lm.c1)$r.squared
# 0.3578332 입니다.
# 다시 그림을 보면
# R 제곱은 b + c + d 에 해당하는
# 것이라고 했고
# semi-partial 값을 각각 구하여
# 이를 제곱하여 더한 것이 b와 d입니다.
# 그런데 그림을 보면 b + d > b + c + d 가
# 됩니다. 그렇지만 그림대로라면
# 이것은 말이 되지 않습니다. 그런데
# 계산값을 이를 가르키고 있습니다.
# 이 이유가 뭘까요?
# 여러분의 생각 후에 mediator 분석에 대해서
# 설명을 하도록 하겠습니다.
Making Questionnaire
Questions you submit at the ajoubb.
Then we will list questions in Google docs Google survey