pre-assumptions_of_regression_analysis
Table of Contents
pre-asumptions in regression test
- Linearity - the relationships between the predictors and the outcome variable should be linear
- Normality - the errors should be normally distributed - technically normality is necessary only for the t-tests to be valid, estimation of the coefficients only requires that the errors be identically and independently distributed
- Homogeneity of variance (or Homoscedasticity) - the error variance should be constant
- Independence - the errors associated with one observation are not correlated with the errors of any other observation
- Model specification - the model should be properly specified (including all relevant variables, and excluding irrelevant variables)
- Influence - individual observations that exert undue influence on the coefficients
- Collinearity or Singularity - predictors that are highly collinear, i.e. linearly related, can cause problems in estimating the regression coefficients.
Outliers
For an example of dealing with outlier, see Outliers
| Model Summary(b) | |||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate | Durbin-Watson |
| 1 | 0.375935755 | 0.141327692 | 0.093623675 | 277.9593965 | 1.770202598 |
| a Predictors: (Constant), income | |||||
| b Dependent Variable: sales | |||||
| ANOVA(b) | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 228894.3304 | 1 | 228894.3304 | 2.962595204 | 0.102353085 |
| Residual | 1390705.67 | 18 | 77261.42609 | |||
| Total | 1619600 | 19 | ||||
| a Predictors: (Constant), income | ||||||
| b Dependent Variable: sales | ||||||
| Coefficients(a) | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | 524.9368996 | 176.8956007 | 2.967495504 | 0.008247696 | |
| income | 0.527406291 | 0.306414384 | 0.375935755 | 1.721219104 | 0.102353085 | |
| a Dependent Variable: sales | ||||||
Note, R2 = .141
Further, Anova test shows that the model is not significant, which means that the IV (income) does not seem to be related (or predict) the sales.
Since F test failed, t-test for B also failed.
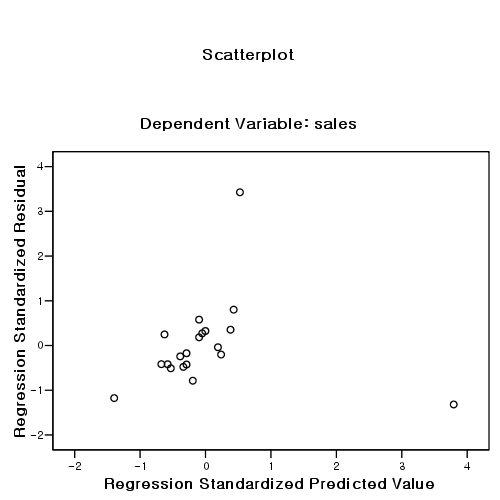
But, the result might be due to some outliers. So, check outliers by examining:
- scatter plot: (z-predicted(x), z-residual(y)). The shape should be rectangular.
- Mahalanobis distance score
- Cook distance
- Leverage
| Casewise Diagnostics(a) | ||||
| Case Number | Std. Residual | sales | Predicted Value | Residual |
| 10 | 3.425856521 | 1820 | 867.7509889 | 952.2490111 |
| a Dependent Variable: sales | ||||
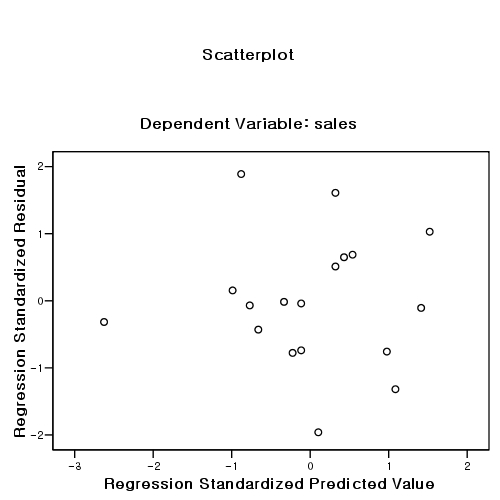
두 개의 케이스를 제거한 후의 분석:
r2 값이 14%에서 70% 로 증가하였다.
독립변인 income의 b 값이 0.527406291에서 1.618765817로 증가 (따라서, t value도 증가) 하였다.
| Model Summary(b) | |||||
| Model | R | R Square | Adjusted R Square | Std. Error of the Estimate | Durbin-Watson |
| 1 | 0.836338533 | 0.699462142 | 0.680678526 | 100.2063061 | 1.559375101 |
| a Predictors: (Constant), income | |||||
| b Dependent Variable: sales | |||||
| ANOVA(b) | ||||||
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 373916.9174 | 1 | 373916.9174 | 37.23788521 | 1.52771E-05 |
| Residual | 160660.8604 | 16 | 10041.30378 | |||
| Total | 534577.7778 | 17 | ||||
| a Predictors: (Constant), income | ||||||
| b Dependent Variable: sales | ||||||
| Coefficients(a) | ||||||
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | -42.98345338 | 132.2567413 | -0.325000094 | 0.749391893 | |
| income | 1.618765817 | 0.265272066 | 0.836338533 | 6.102285245 | 1.52771E-05 | |
| a Dependent Variable: sales | ||||||
Normality
Normality
Data: elemapi2.sav
get file="drivename:\\elemapi2.sav". regression /dependent api00 /method=enter meals ell emer /save resid(apires). examine variables=apires /plot boxplot stemleaf histogram npplot.
Homoscedasticity
Homoscedasticity
The distribution of residual along the x-values (independent values) should NOT have a pattern.
Multi-collinearity
- It is about correlations among IVs
- Why? . . . .
Nonlinearity
case number
- About 20 times than IV numbers.
- When you have 5 IVs, you need 5 * 20 = 100 cases.
- Minimum is said to be 5 times (instead of 20 times).
pre-assumptions_of_regression_analysis.txt · Last modified: by hkimscil