types of error, 오류의 종류, 1종 오류, 2종 오류, type I error, type II error
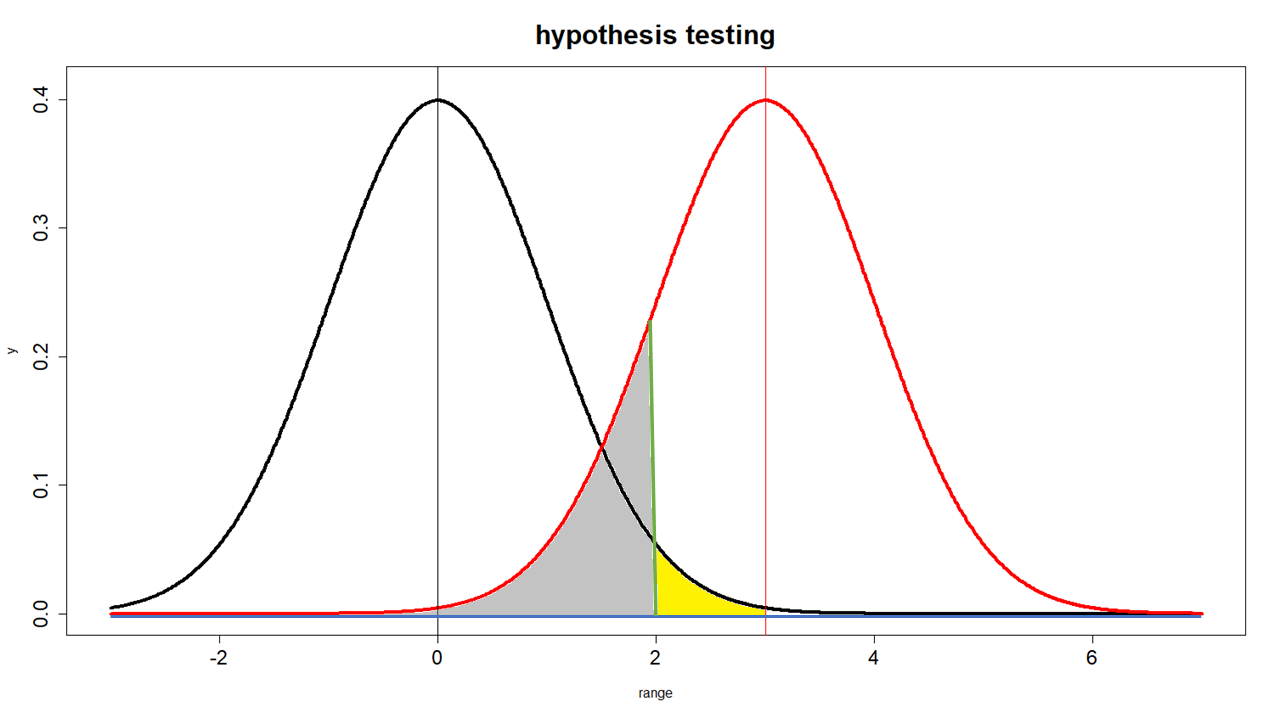
Types of error
- black line(bl): $\overline{x}=0, \text{sd}=1$ 정규분포곡선 = 영가설 Null Hypothesis
- red line(rl): $\overline{x}=3, \text{sd}=1$ 정규분포곡선 = 연구가설 Alternative Hypothesis
- green line: 가설테스트를 했을 때 영가설을 부정하게 되는 기준 (sd=2).
- 노란색 부분: type I error
- 회색 부분: type II error
설명
- H1: $\mu_{\text{black}} \neq \mu_{\text{red}} \;\;\; (0 \neq 3) $
- H0: $\mu_{\text{black}} = \mu_{\text{red}} \;\;\; (0 = 3) $
- H1: 새로운 약의 효과는 기존 약과 다를 것이다.
- H0: 새로운 약의 효과가 없을 것이다.
실제 현상이 (약의 효과가) 있는 것으로 가정하면 붉은 선이 현실이 된다. 그러나 연구자는 붉은 선은 가정을 할 뿐, 실제로는 알 수 없으며, 검은 선을 가지고 (즉 영가설을 가지고) 판단을 하게 된다. 이 때 판단의 기준은 녹색 선이며, 이는 SE 단위 둘을 사용한 .05를 가르킨다.
Type I Error
가설검증을 위해서 녹색선을 사용하였을 때, 샘플의 평균이 노란색 부분에서 나타났다면, 연구자는 이것이 영가설의 평균과 통계적으로 유의미한 차이를 나타내 주는 것이라고 생각한다. 따라서 영가설을 부정하고 연구가설을 지지하게 된다. 즉, 영가설은 거짓이며, 연구가설은 참이라고 결론을 내린다 (테이블에서 A). 만약에 사실은 이 평균이 검은색의 모집단에서 나온 것이라면 (즉, 영가설 집단에서 나온 것이라면 혹은 1/20의 샘플링 확률에 걸린 것이라면), 연구자는 영가설이 참, 연구가설이 거짓인 실제(reality)를 영가설이 거짓, 연구가설이 참으로 결론 지은 것이 된다 (B). 이렇게 잘못 결론지을 확률이 .05이다. 이를 type I error라고 부르며, 이는 연구자가 가설검증을 설계할 단계에 이를 미리 지정해 놓고 알고 있는 (감수하고 있는) 오차의 한계이다. 이것을 알파($\alpha$)라고도 부른다.
Type II Error
그러나, 만약에 샘플의 평균이 회색 부분의 선에서 나타났다면, 연구자는 critical region을 넘지 못하였으므로 이것을 영가설의 모집단에서 나온 샘플의 평균으로 생각하게 된다. 따라서 영가설 부정에 실패하여, 연구가설을 지지하지 못하게 된다 (C). 그런데, 사실은 그 샘플의 평균이 붉은선의 모집단에서 나왔다고 한다면, 옳은 결론은 영가설은 거짓이어야 한다. 그런데, 이 가설검증에서 연구자는 영가설이 참, 따라서 연구가설은 거짓으로 잘못 진단한 것이다 (D). 이 범위를 type II error 혹은 베타($\beta$)라고 한다.
위의 설명은 아래 표와 같이 정리할 수 있다.
| Table of types of error | Null Hypothesis(H0)가 | ||
|---|---|---|---|
| Valid/True | Invalid/False | ||
| Null Hypothesis (H0)에 대한 판단 | Reject (부정) | B: Type I error (alpha) | A: 옳은 결정 |
| Fail to reject (부정에 실패) | C: 옳은 결정 | D: Type II error (beta) |
|
알파의 경우는 연구자가 정하는 방법으로 컨트롤할 수 있다. 그러나, 베타의 경우는 알파와 같은 방법을 사용할 수는 없다. 베타를 줄이는, 즉 영가설이 거짓으로 부정을 해야하는데 그렇게 하지 못하는 경우를 줄이는 방법으로 상식, 보편적인 것은 샘플의 n을 키우는 것이다. 좀 더 설명하자면, 위의 그래프 figure 1에서 각각은 샘플링분포곡선을 의미하므로 각 라인의 표준편차는 표준오차를 의미한다. 표준오차가를 줄이게 되면 두 라인이 서로 겹쳐질 경우가 줄어들게 되고, 이는 곧 베타의 감소를 의미한다.
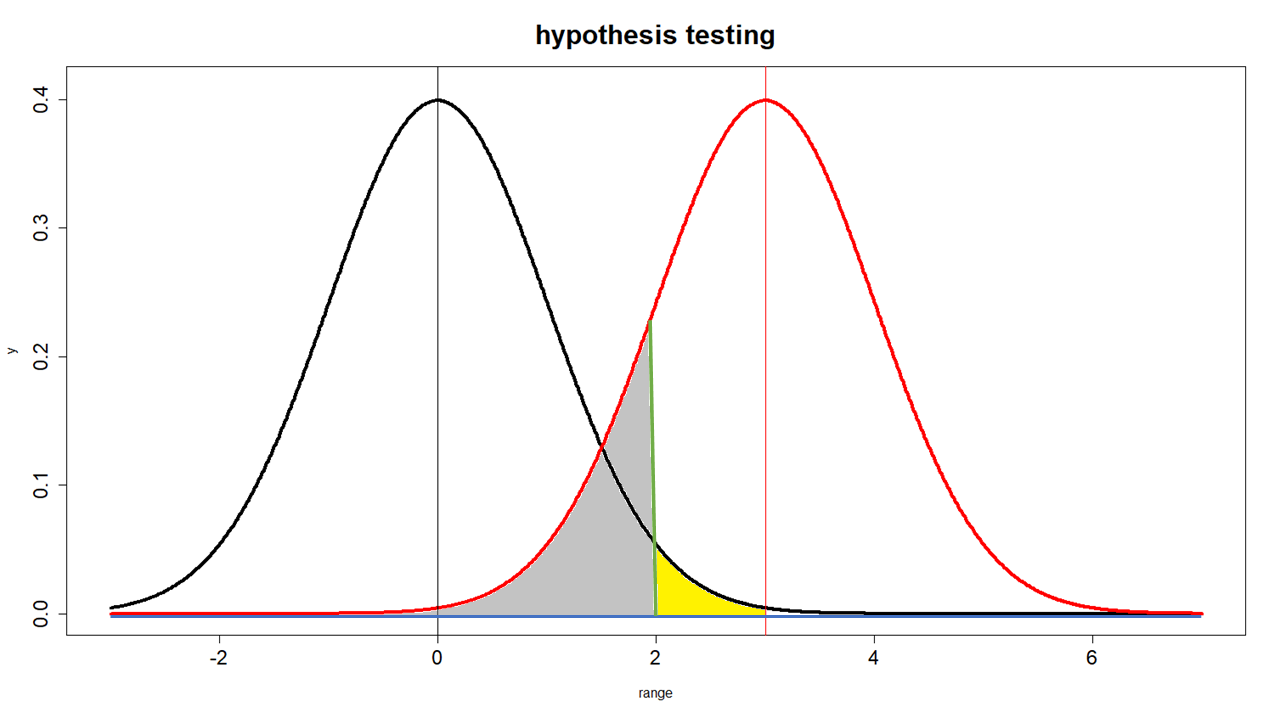 Fig. 1: standard error = 1 일 경우
Fig. 1: standard error = 1 일 경우
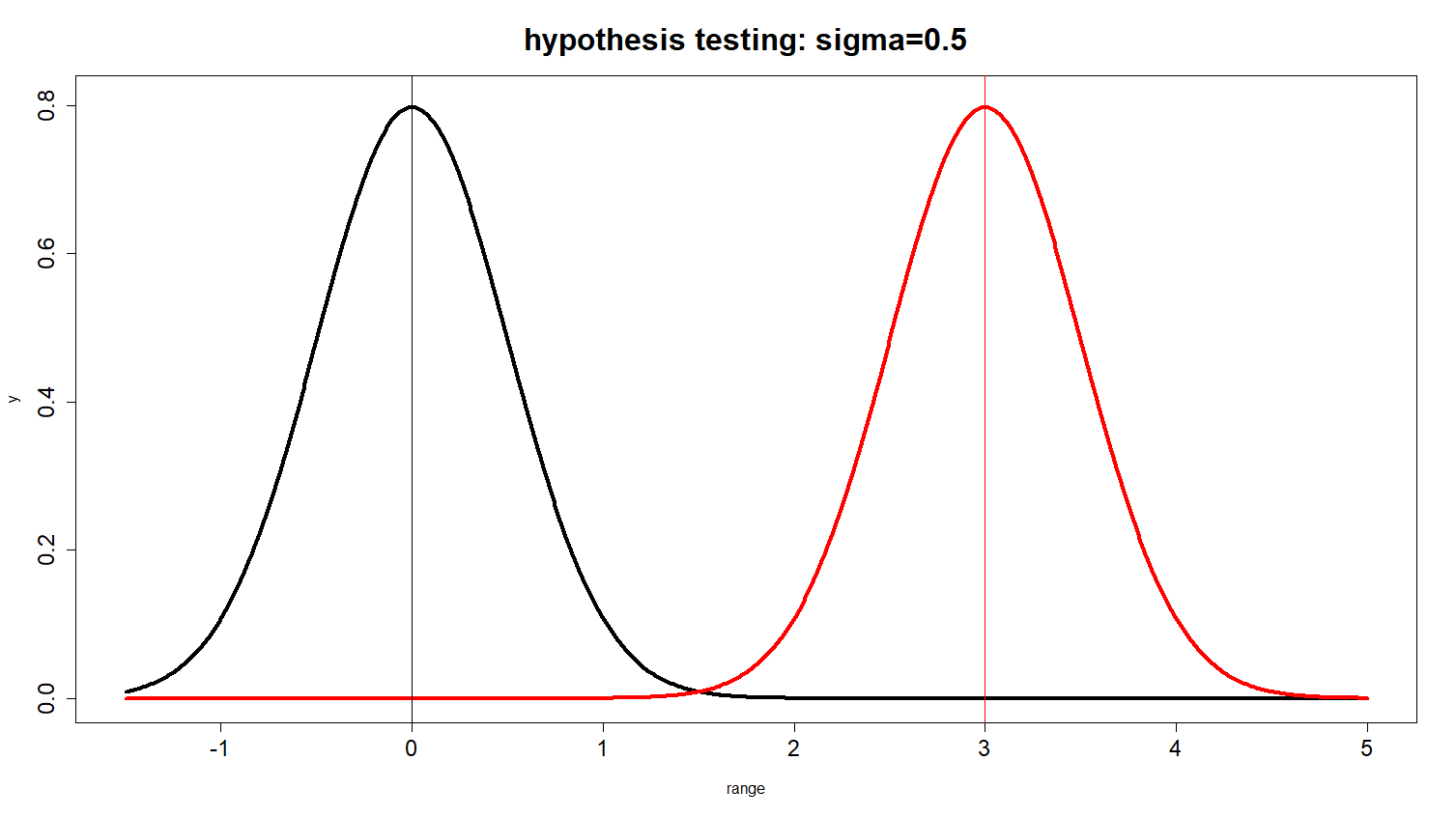 Fig. 3: standard error = 0.5 일 경우. 회색부분이 생길 가능성이 거의 없다는 것에 주목하라.
Fig. 3: standard error = 0.5 일 경우. 회색부분이 생길 가능성이 거의 없다는 것에 주목하라.
E.G.
이는 아래를 보면 더 확연해진다.
rnorm2 <- function(n,mean,sd) { mean+sd*scale(rnorm(n)) }
potato_sample <- rnorm2(25, 194,20)
mean(potato_sample)
sqrt(var(potato_sample))
t.test(potato_sample, mu=200)
One Sample t-test
data: potato_sample
t = -1.5, df = 24, p-value = 0.1467
alternative hypothesis: true mean is not equal to 200
95 percent confidence interval:
185.7444 202.2556
sample estimates:
mean of x
194
>
아래의 qt 펑션 이해를 위해서는 t-distribution function 문서 참조
> abs(qt(0.05/2, 24)) [1] 2.063899
즉, +-2.063899 이상이 되어야지 영가설을 부정할 수 있는데, 현재의 t-score는 -1.5이므로 영가설을 부정할 수 없는 상태이다.
se 값을 구하는 공식으로 sqrt(25)=5 이니 se = 20/5 = 4 이다. 만약에 n값이 (샘플사이즈) 2500 이라면 se값은 0.4일 것이다 (아래 참조)
> 20/sqrt(length(potato_sample)) [1] 4
potato_sample_large <- rnorm2(2500, 194,20)
mean(potato_sample_large)
[1] 194
> sqrt(var(potato_sample_large))
[1] 20
t.test(potato_sample_large, mu=200)
One Sample t-test
data: potato_sample_large
t = -15, df = 2499, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 200
95 percent confidence interval:
193.2156 194.7844
sample estimates:
mean of x
194
> abs(qt(0.05/2, 2499)) [1] 1.960914
위의 경우 critical t value는 +-1.960914 (approx. 2)면 영가설을 부정할 수 있는데, calculated t value는 -15이므로 부정할 수 있다.
> # standard error value > 20/sqrt(length(potato_sample_large)) [1] 0.4 >
위 둘의 se를 비교해 보라. 그리고, 이를 type I and type II error와 관련지어 설명하라
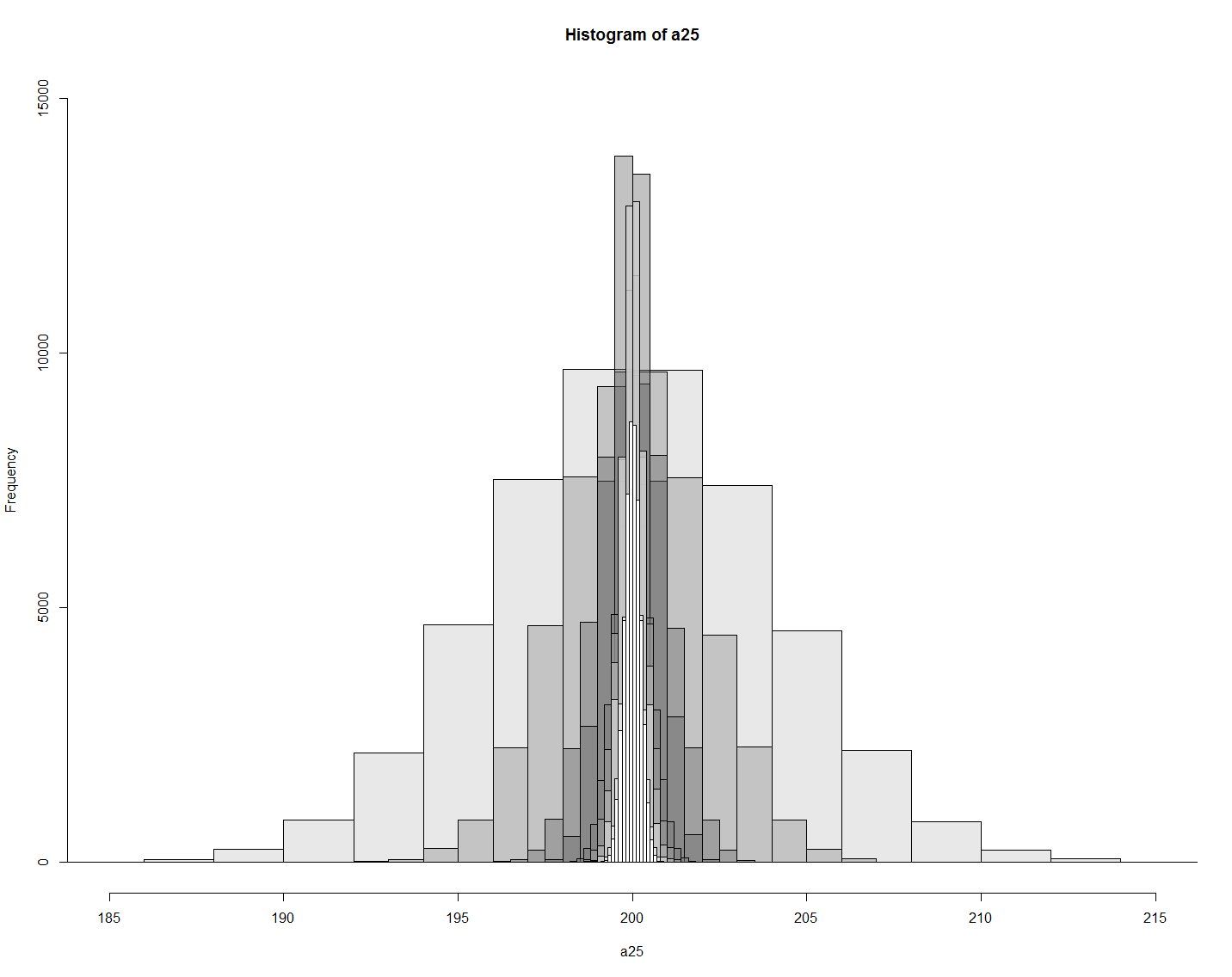
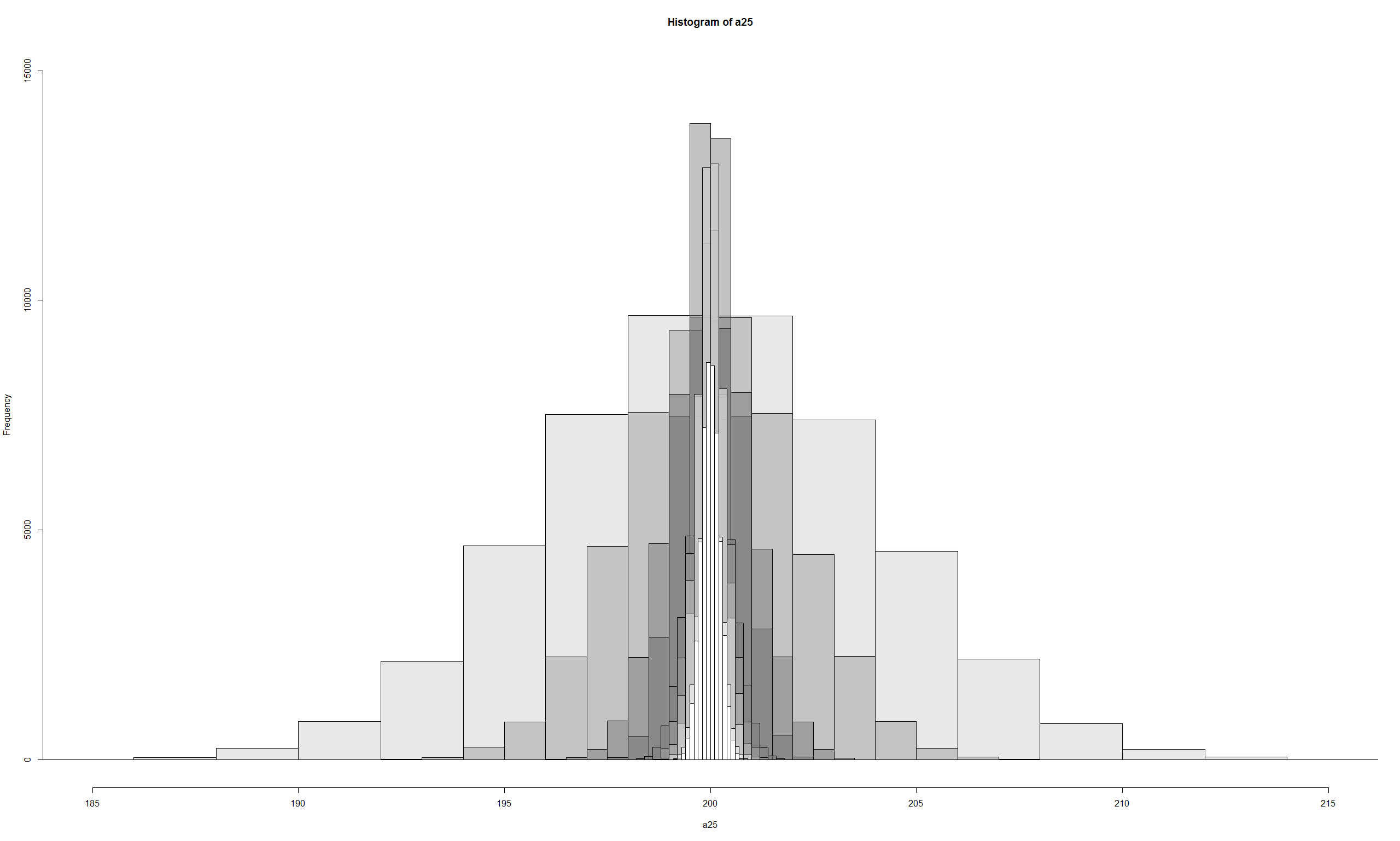
mu = 200, sigma = 20 인 상황에서 a___ 뒤의 숫자가 샘플의 크기라고 하면,
> a25 <- rnorm(50000, 200, 4) # 4 = 20/sqrt(25) = std error값 > a100 <- rnorm(50000, 200, 2) > a400 <- rnorm(50000, 200, 1) > a900 <- rnorm(50000, 200, .667) > a1600 <- rnorm(50000, 200, .5) > a2500 <- rnorm(50000, 200, .4) > a3600 <- rnorm(50000, 200, .333) > a4900 <- rnrom(50000, 200, .286) > a6400 <- rnorm(50000, 200, .25) > a8100 <- rnorm(50000, 200, .222) > pa25 <- hist(a25) > pa100 <- hist(a100) > pa400 <- hist(a400) > pa900 <- hist(a900) > pa1600 <- hist(a1600) > pa2500 <- hist(a2500) > pa3600 <- hist(a3600) > pa4900 <- hist(a4900) > pa6400 <- hist(a6400) > pa8100 <- hist(a8100) > plot(pa25, col=rgb(.1,.1,.1,.1), xlim=c(185,215), ylim=c(0,15000)) > plot(pa100, col=rgb(.2,.2,.2,.2), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa400, col=rgb(.3,.3,.3,.3), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa900, col=rgb(.4,.4,.4,.4), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa1600, col=rgb(.5,.5,.5,.5), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa2500, col=rgb(.6,.6,.6,.6), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa3600, col=rgb(.7,.7,.7,.7), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa4900, col=rgb(.8,.8,.8,.8), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa6400, col=rgb(.9,.9,.9,.9), xlim=c(185,215), ylim=c(0,15000), add=T) > plot(pa8100, col=rgb(1,1,1,1), xlim=c(185,215), ylim=c(0,15000), add=T)
sampling_distribution_25_to_8100.pdf
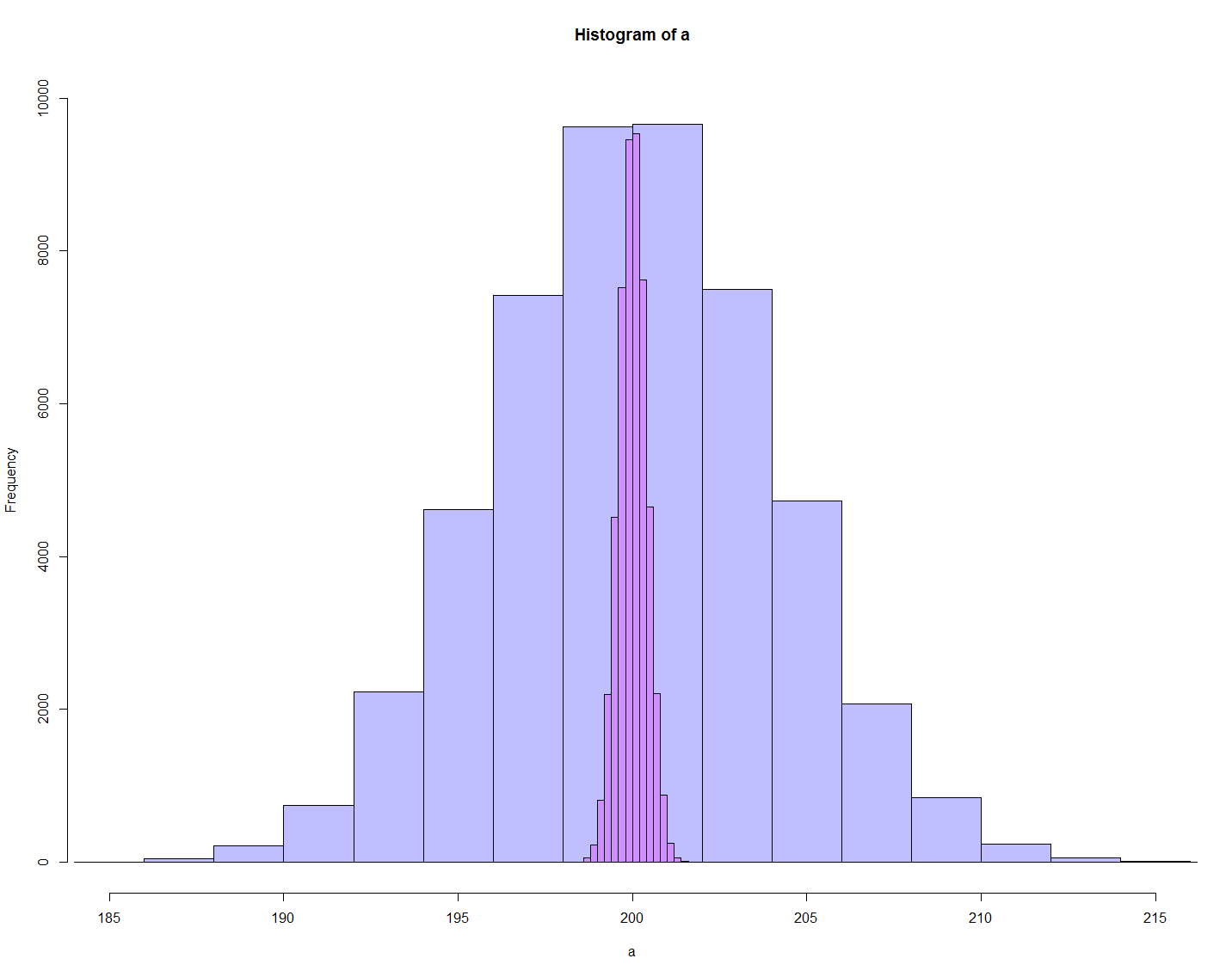
Where is my 194 (sample's mean)?